FFNと活性化関数の実装:4倍拡張MLPと非線形変換の理論
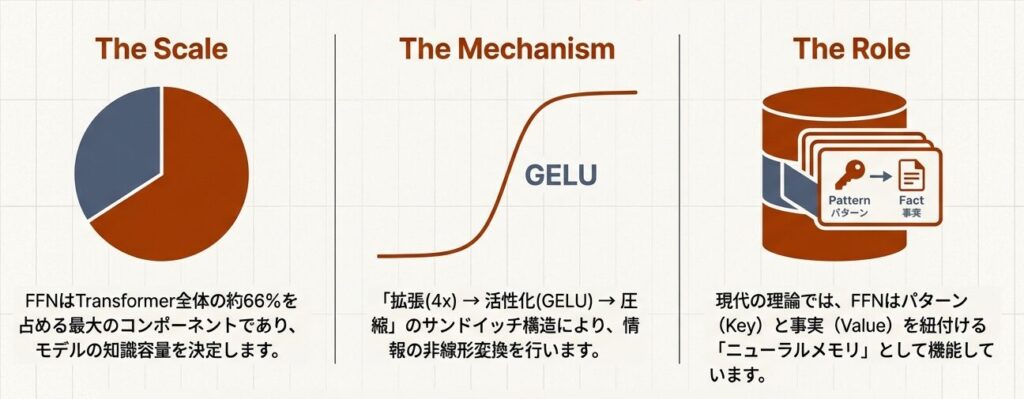
Transformerモデルのパラメータの66%はFFN層に集中しています。この一見シンプルな2層MLPが、なぜこれほど大きな役割を担うのか。本記事では、FFNの詳細構造と活性化関数の選択について、実装レベルで解説します。
FFNと活性化関数についての構造については下記を参照してください。
【FFNと活性化関数の詳細】

Feed Forward Network (FFN) の詳細構造
Attentionが「どこを見るか」を決めるなら、FFNは「何を知っているか」を決定します。GPT-3をはじめとするLLMの知識の泉、その巨大なメカニズムに迫ります。
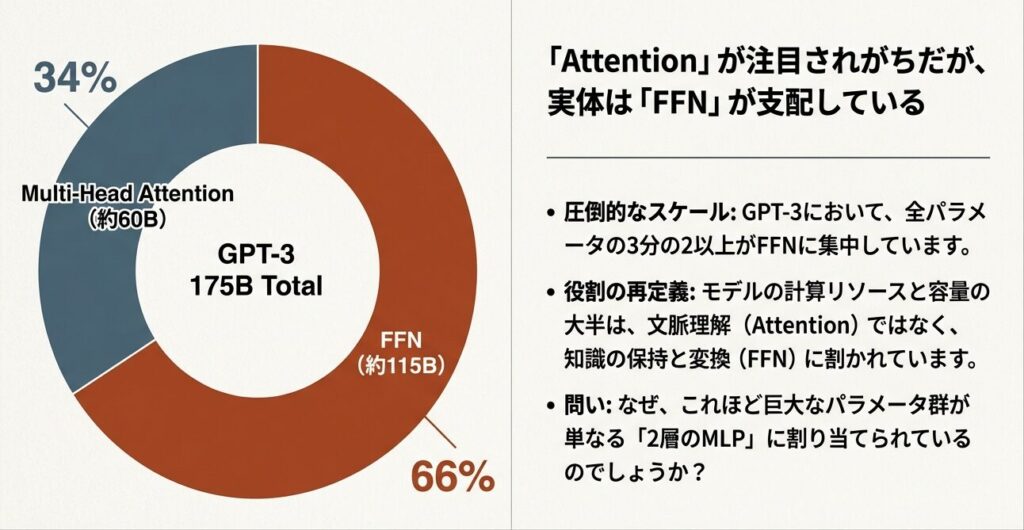
2層MLP構造の全体像
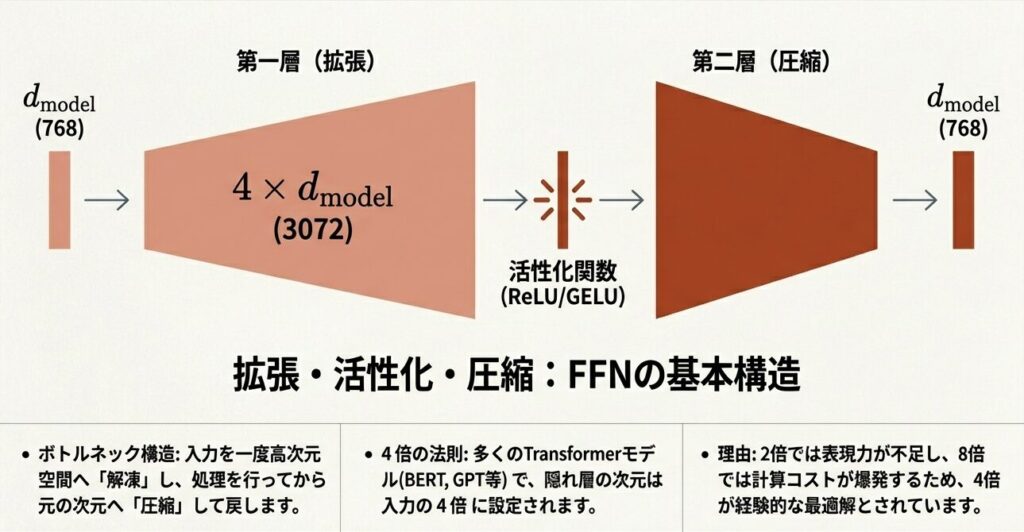
FFNは「拡張 → 活性化 → 圧縮」という3ステップで構成されます。
入力:(batch, seq_len, d_model) = (32, 100, 768)
ステップ1:拡張層
出力 = 入力 @ W_1 + b_1
形状:(32, 100, 768) @ (768, 3072) + 3072
= (32, 100, 3072)
拡張比:768 → 3072 = 4倍
ステップ2:活性化関数(GELU)
出力 = GELU(中間)
形状:(32, 100, 3072) (形状変わらず)
ステップ3:圧縮層
出力 = 活性化後 @ W_2 + b_2
形状:(32, 100, 3072) @ (3072, 768) + 768
= (32, 100, 768)
最終出力:(32, 100, 768) (元の形に戻る)なぜ4倍拡張なのか?
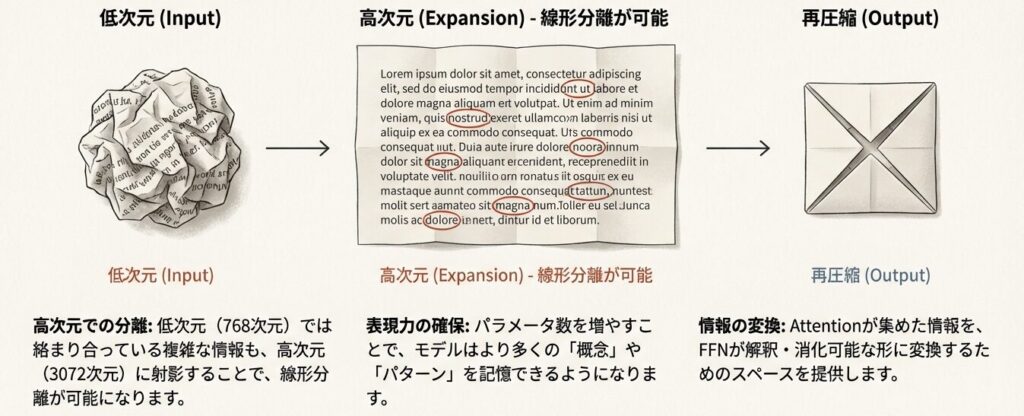
理由1:表現力の確保
- 768次元の情報を3072次元に拡張することで、より複雑な非線形変換が可能
- 拡張後に活性化関数を適用 → 非線形な特徴抽出
理由2:経験的な最適値
- 2倍では表現力不足
- 8倍ではパラメータ数が爆発
- 4倍が精度とコストのバランス点
パラメータ数の計算
FFNのパラメータは拡張(W1,b1)と圧縮(W2,b2)の重み・バイアスの合計です。
W1=768×3072=2,359,296、W2=3072×768=2,359,296、b1=3072、b2=768で合計約4.7M。12層で約56.4Mになり、175Bモデルの約32%を占めます。
W_1 パラメータ数:768 × 3072 = 2,359,296
W_2 パラメータ数:3072 × 768 = 2,359,296
b_1 パラメータ数:3072
b_2 パラメータ数:768
FFN合計:約4.7百万パラメータ(1層当たり)
全12層合計:4.7M × 12 = 56.4M
全モデル(175B GPT-3)の約32%活性化関数の詳細と性質
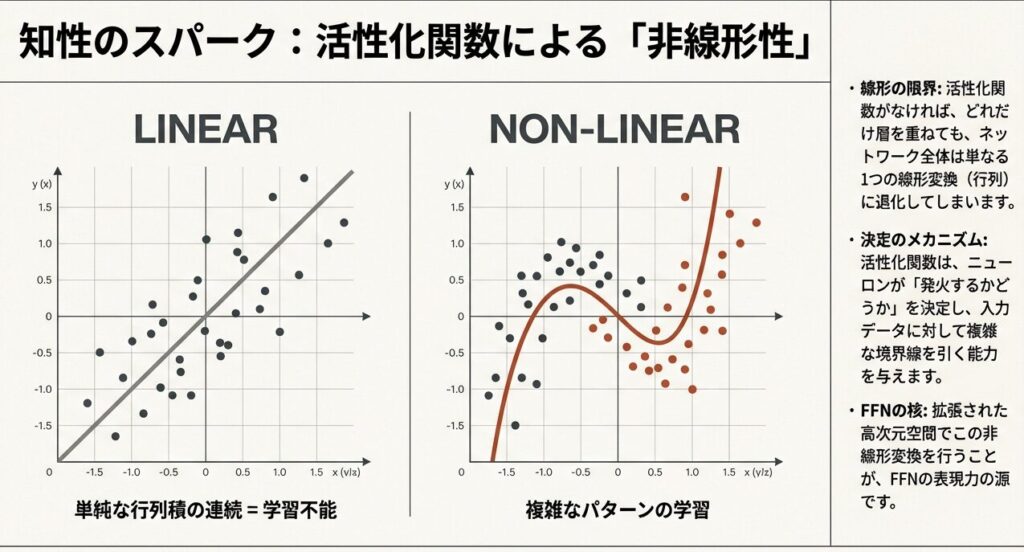
FFNに活性化関数が必要なのは、線形変換のみだと合成しても線形のままで表現力が不足するため。非線形性を導入することで複雑な関数を学習し、特徴抽出や出力の選択性・勾配の性質(滑らかさや安定性)を改善します。
【FFNにおける活性化関数の詳細について】

ReLU (Rectified Linear Unit)
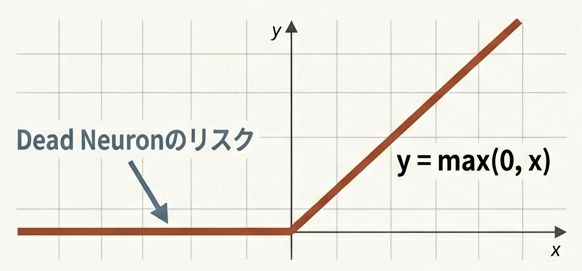
シンプルで計算コストが低いが、負の値が全て0になるため、学習が進まなくなる「Dead Neuron」問題が発生しやすい。
$$\text{ReLU}(x) = \max(0, x)$$
入力:[-2.0, -1.0, 0.0, 1.0, 2.0]
出力:[ 0.0, 0.0, 0.0, 1.0, 2.0]
性質:
- 計算が単純で高速
- 勾配が消失しない(正の領域)
- Dead ReLU問題:負の値で勾配が0Dead ReLU問題の例:
大量の入力が負値 → 勾配が常に0 → 学習が進まない
例:学習中に特定のニューロンが常に負の入力を受ける
→ そのニューロンの重みは永遠に更新されない
→ モデルの表現力低下GELU (Gaussian Error Linear Unit)
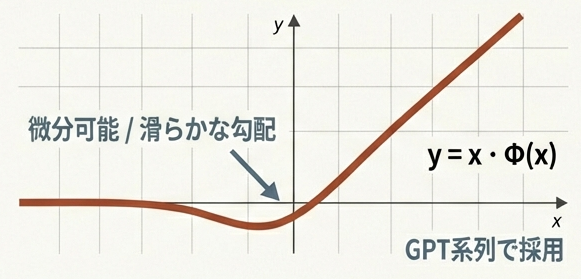
正規分布の累積分布関数を用いた確率的な解釈を持つ関数。
$$\text{GELU}(x) = x \cdot \Phi(x)$$
ここで $\Phi(x)$ は標準正規分布の累積分布関数。
近似式:
GELU(x) ≈ 0.5 × x × (1 + tanh(√(2/π) × (x + 0.044715 × x³)))
入力:[-2.0, -1.0, 0.0, 1.0, 2.0]
出力:[-0.05, -0.16, 0.0, 0.84, 1.96]GELUの特性:
- ReLUよりなめらか(微分可能)
- 確率的解釈:正規分布の累積分布
- 現在のLLMで標準的な活性化関数
- 計算コストがReLUより高い
ReLU vs GELU 比較表
| 項目 | ReLU | GELU |
|---|---|---|
| 計算コスト | 低(比較演算のみ) | 中(指数関数) |
| 勾配の滑らかさ | 不連続 | 連続的 |
| 負の値の出力 | 0固定 | 小さな負の値 |
| Dead Neuron問題 | あり | なし |
| 現代LLMでの採用 | 少 | ほぼ標準 |
現代LLMの標準:GELUの数学的優位性

GELUは0付近で滑らかに変化し、小さな負の値を許容するため、勾配消失を防ぎ、より安定した学習が可能です。但し現在のLLMモデル(2026年1月)ではSwiGLUが主流として用いられています。
【SwiGLUを提案した、最も重要で直接的な論文】
- GLU Variants Improve Transformer, Noam Shazeer(2020): “GLU Variants Improve Transformer”, arXiv
パラメータ分布の分析
GPT-2サイズモデルのパラメータ内訳
モデルのパラメータはFFNに集中し、Embedding約5%、Attention約25%、FFN約60%、出力約10%程度を占める。
パラメータ分布(GPT-2相当):
- Embedding層:約5%(語彙×次元)
- Self-Attention層:約25%(Q,K,V,O各行列)
- FFN層:約60%(W_1は768×3072, W_2は3072×768で大型)
- Output層:約10%なぜFFNが大きいのか?
FFNは「Key-Value メモリ」である
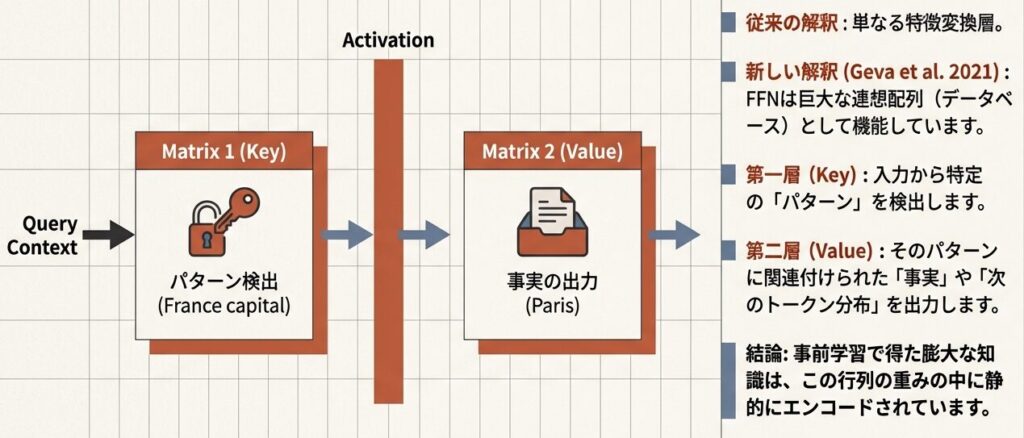
FFNが大きい理由はd_model→4×d_modelの拡張によりW1,W2が大行列になり、Attentionの重み合計より概ね2倍のパラメータ量になるため。
計算で確認:
Attention層のパラメータ(1層):
W_Q: 768 × 768 = 589,824
W_K: 768 × 768 = 589,824
W_V: 768 × 768 = 589,824
W_O: 768 × 768 = 589,824
合計: 約2.4M
FFN層のパラメータ(1層):
W_1: 768 × 3072 = 2,359,296
W_2: 3072 × 768 = 2,359,296
合計: 約4.7M
比率: FFN / Attention = 4.7M / 2.4M ≈ 2倍FFNが大きい理由:
- 4倍拡張による行列サイズの増大
- 拡張・圧縮の両方向で大行列が必要
- Attentionは「関係性の発見」、FFNは「情報の変換」という役割分担
疑似コード実装
FFN層の実装
初期化(__init__):
- W_1(768×3072)とW_2(3072×768)の重み行列、b_1とb_2のバイアスを初期化
- 入出力次元d_model=768、中間次元d_ff=3072(4倍拡張)を設定
順伝播(forward):
- 拡張:入力xをW_1で768→3072次元に拡張
- 活性化:GELU関数で非線形変換(Dead ReLU問題を回避)
- 圧縮:W_2で3072→768次元に戻す
結果として入力と同じ形状(batch, seq_len, 768)の出力を返します。このシンプルな2層MLPが、モデルパラメータの約60%を占める「メモリ」として機能し、事実知識を格納します。
class FeedForwardNetwork:
def __init__(self, d_model=768, d_ff=3072):
"""
パラメータ:
d_model: 入出力の次元(768)
d_ff: 中間層の次元(3072 = 4 × d_model)
"""
self.d_model = d_model
self.d_ff = d_ff
# 重み行列の初期化
self.W_1 = initialize_weights((d_model, d_ff)) # 拡張層
self.W_2 = initialize_weights((d_ff, d_model)) # 圧縮層
self.b_1 = initialize_zeros(d_ff)
self.b_2 = initialize_zeros(d_model)
def forward(self, x):
"""
入力: x (batch, seq_len, d_model)
出力: (batch, seq_len, d_model)
"""
# ステップ1: 拡張
expanded = matrix_multiply(x, self.W_1) + self.b_1
# 形状: (batch, seq_len, d_ff)
# ステップ2: 活性化(GELU)
activated = gelu(expanded)
# 形状: (batch, seq_len, d_ff)
# ステップ3: 圧縮
output = matrix_multiply(activated, self.W_2) + self.b_2
# 形状: (batch, seq_len, d_model)
return output活性化関数の実装
GELU(x) = x × Φ(x)は、入力xに標準正規分布の累積分布関数を乗じた活性化関数で、ReLUより滑らかでLLMの標準です。
def relu(x):
"""ReLU: max(0, x)"""
return maximum(0, x)
def gelu(x):
"""
GELU: x * Φ(x)
近似実装(高速版)
"""
return 0.5 * x * (1 + tanh(
sqrt(2 / pi) * (x + 0.044715 * x**3)
))
# 数値例
x = array([-2.0, -1.0, 0.0, 1.0, 2.0])
print("ReLU:", relu(x)) # [0, 0, 0, 1, 2]
print("GELU:", gelu(x)) # [-0.05, -0.16, 0, 0.84, 1.96]SwiGLU活性化関数の実装
現在のLLMモデル(2026年1月)ではSwiGLUが主流として用いられています。
def swish(x):
"""Swish: x * sigmoid(x)"""
return x * sigmoid(x)
def swiglu(x, W_gate=None):
"""
SwiGLU: (x @ W) * swish(x @ W_gate)
GLU(Gated Linear Unit)にSwishを組み合わせた活性化関数
パラメータ:
x: 入力 (batch, seq_len, d_model)
W_gate: ゲート用の重み(ここでは簡略化)
"""
# 拡張層の出力を半分に分割
split = x.shape[-1] // 2
x_main = x[:, :, :split] # 値として機能
x_gate = x[:, :, split:] # ゲートとして機能
# Swish活性化でゲートを計算
gate = swish(x_gate)
# 要素ごとの乗算(GLUメカニズム)
return x_main * gate
# 数値例
x = array([-2.0, -1.0, 0.0, 1.0, 2.0, -1.5, 0.5, 1.5, -0.5, 0.0])
print("Swish:", swish(x)) # [-0.15, -0.27, 0.0, 0.73, 1.76, ...]
print("SwiGLU:", swiglu(x)) # (値とゲートの要素積)SwiGLUの特性:
- Swish活性化とGLU(Gated Linear Unit)の組み合わせ
- FFNの拡張次元を2倍に増やす必要がない(ゲート分割で効率化)
- 計算効率とモデル性能のバランスでLLaMA等の最新モデルで採用
- GELUより計算コストが低い
FFNの役割と重要性
Attention vs FFNの役割分担
Attentionの「文脈」とFFNの「記憶」
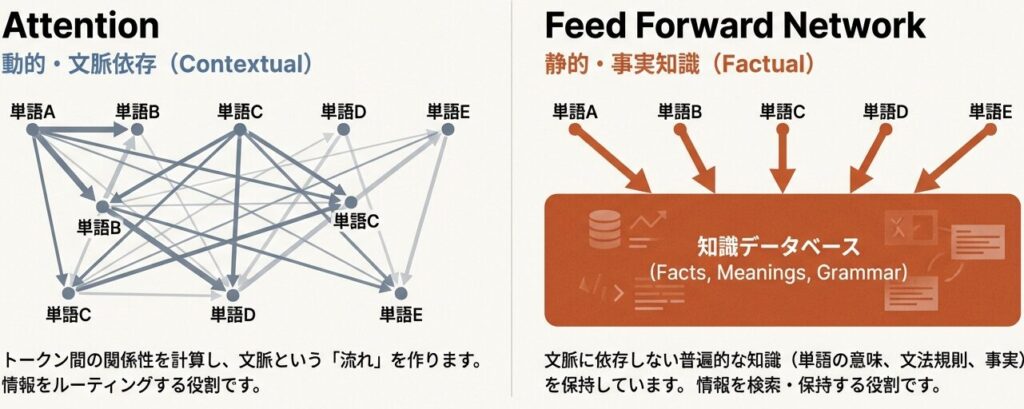
協調動作:
Attentionが「検索クエリ」を作成し、FFNがそのクエリに応答して「知識」を提供する、というサイクルを繰り返します。
【Attention層の役割】
- トークン間の「関係性」を発見
- 「どの情報に注目すべきか」を学習
- 長距離依存関係の捕捉
【FFN層の役割】
- 各トークンの「特徴変換」
- 「情報をどう変換すべきか」を学習
- 非線形な知識の格納
- 「メモリ」としての機能FFNは「メモリ」として機能する
最近の研究では、FFN層が事実知識を格納するメモリとして機能することが示されています。
つまり、FFNの巨大なパラメータ空間こそが、AIが世界を記述するための「記憶」そのものです。
例:「パリはフランスの首都である」
この知識は:
- Attentionで「パリ」と「フランス」の関係を認識
- FFNで「首都」という属性を呼び出し
- 出力層で「首都」を生成
FFNの大きさ ≈ 格納できる知識量📖 参考文献
主要論文
- Hendrycks, D., & Gimpel, K. (2016): “Gaussian Error Linear Units (GELUs)”, arXiv
- Geva, M., Schvartz, R., Shalev-Shwartz, S., & Schwartz, R. (2021): “Transformer Feed-Forward Layers Are Key-Value Memories”, EMNLP 2021
- Lepikhin, D., et al. (2021): “Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity”, JMLR 2022


コメント