Embedding層と入出力形状の追跡:BPEからベクトル化まで
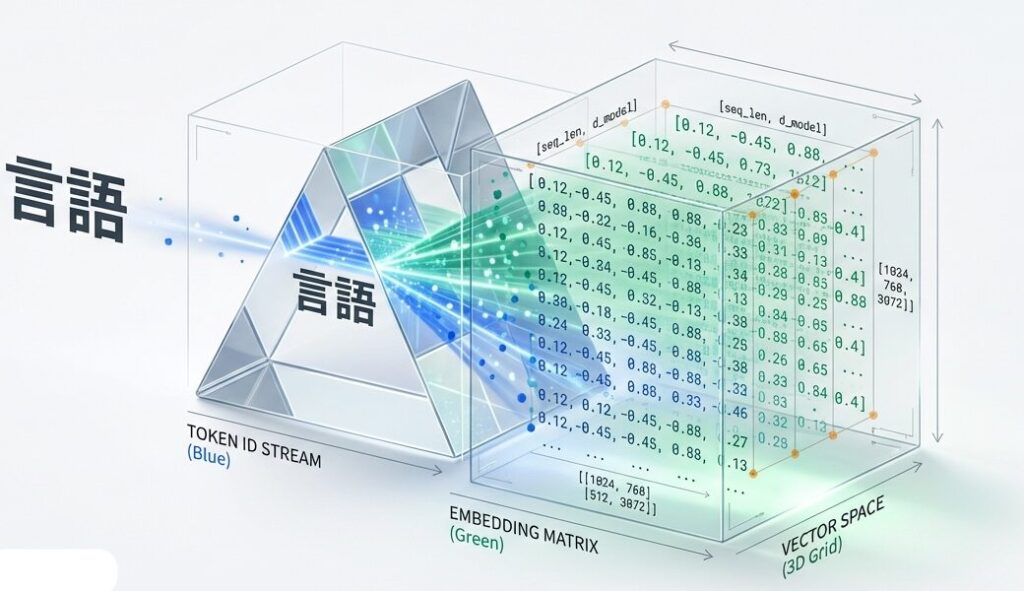
ブログA(基礎理論)では、Transformerの全体構造を学びました。ここからは、各コンポーネントの実装詳細を深掘りしていきます。
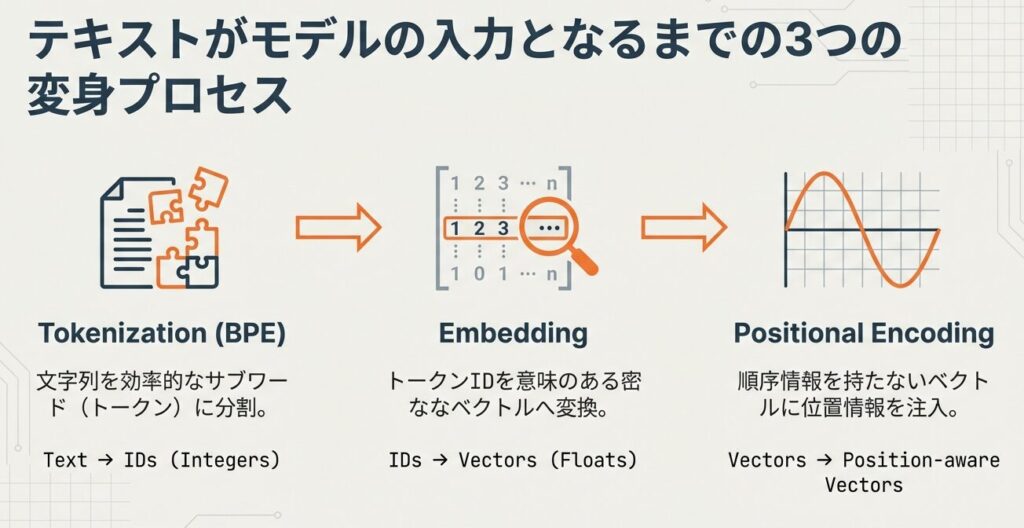
まずは、テキストをモデルが処理できる形式に変換するEmbedding層から始めます。
Byte Pair Encoding (BPE) の詳細実装アルゴリズム
【BPEの詳細】

アルゴリズムの全体像

BPEは、テキストを適切なサイズのトークンに分割するアルゴリズムです。
ステップ1:初期化
入力コーパス:
('hug', 10回)
('pug', 5回)
('pun', 12回)
('bun', 4回)
('hugs', 5回)
文字レベルへの分割:
('h' 'u' 'g', 10) → 出現回数×3 = 30回分のペア
('p' 'u' 'g', 5) → 出現回数×3 = 15回分のペア
('p' 'u' 'n', 12) → 出現回数×3 = 36回分のペア
('b' 'u' 'n', 4) → 出現回数×3 = 12回分のペア
('h' 'u' 'g' 's', 5) → 出現回数×4 = 20回分のペア
単語終了記号を追加(</w>):
('h' 'u' 'g</w>', 10)
('p' 'u' 'g</w>', 5)
... などステップ2:頻出ペアの統合
反復1: 最頻出ペア 'u' + 'g' をマージ → 'ug'
反復2: 最頻出ペア 'u' + 'n' をマージ → 'un'
反復3: 最頻出ペア 'h' + 'ug' をマージ → 'hug'
...ステップ3:語彙サイズに達するまで繰り返し
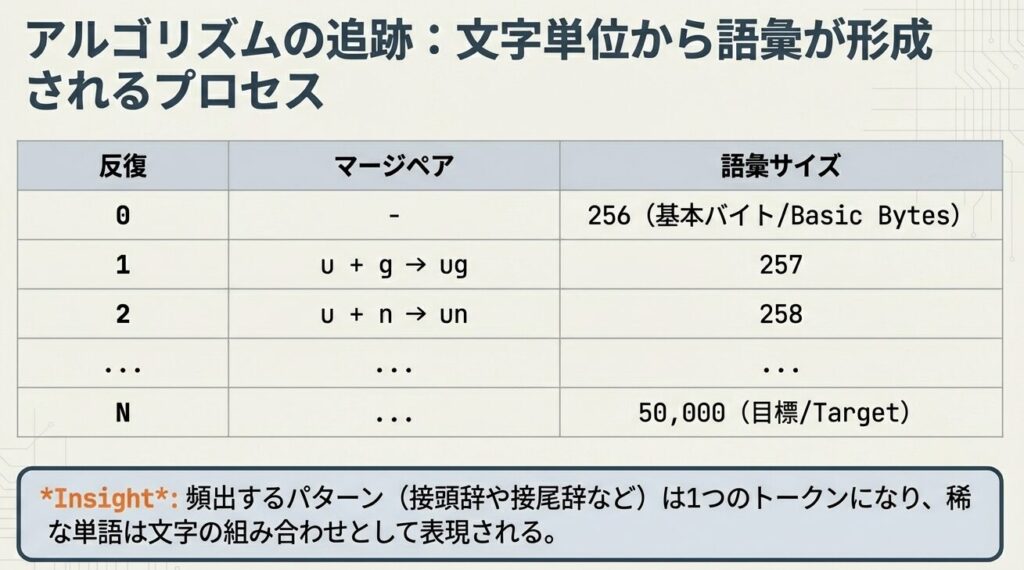
ステップ4:トークン化の結果トークンIDとして表現される
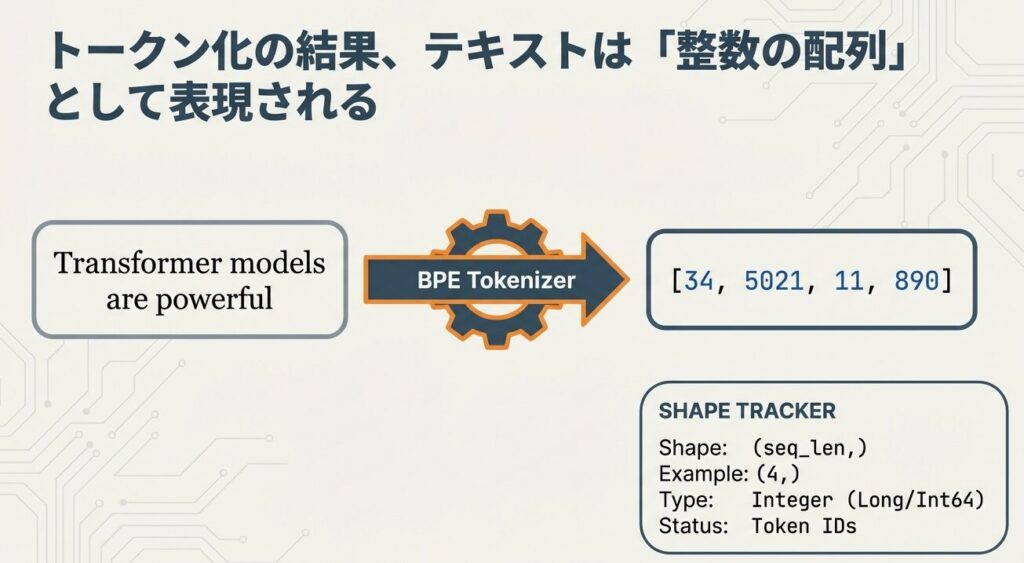
ワードエンベディングの学習と初期化
ワードエンベディングとは?
各トークンIDを、学習可能な数値ベクトルに変換します。学習を通じて、意味的に似た単語は近い位置に配置されます。
単語の意味がベクトルに含まれているという意味
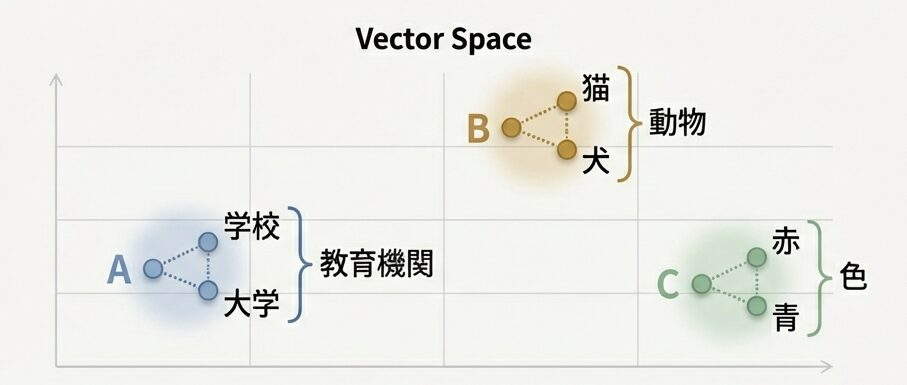
【ワードエンベディングの詳細】

ランダム初期化 vs 事前訓練エンベディング
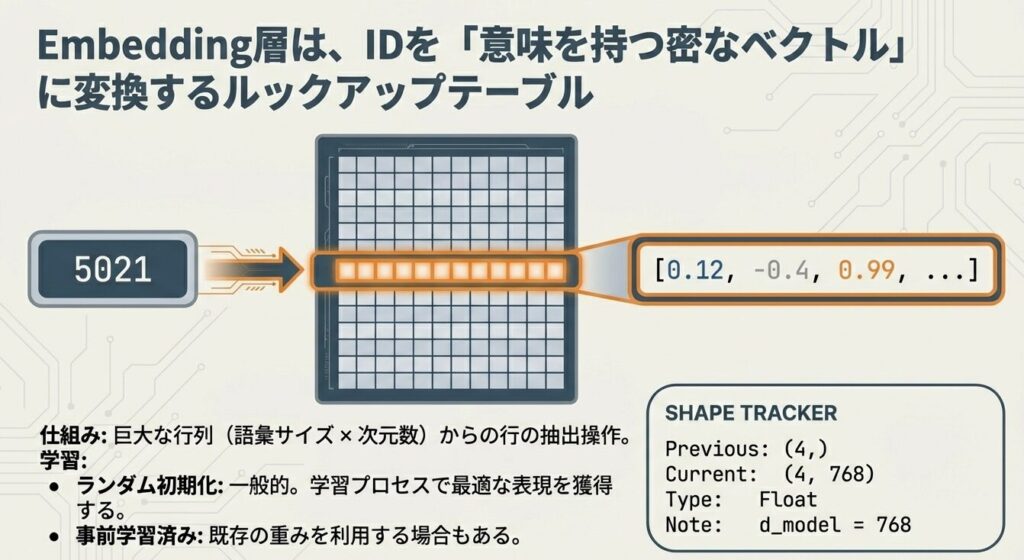
方法1:ランダム初期化(一般的)
# 疑似コード
embedding_matrix = random_normal(vocab_size, embedding_dim)
# 例:vocab_size=50257(GPT-2/3レベル)
# embedding_dim=768
# → パラメータ数:50257 × 768 ≈ 38.6M(約39百万)方法2:事前訓練エンベディングの利用
# Word2Vec, GloVe等の既訓練エンベディングを初期値とする
pretrained_embedding = load_pretrained_embeddings()
embedding_matrix = pretrained_embeddingトークンIDから実ベクトルへの変換

入力テキスト:「私は学校へ」
↓ トークン化
トークン ID:[1050, 80, 2450, 94]
↓ Embedding層を通す
埋め込みベクトル:
[[-0.2, 0.5, 0.1, ...], # 「私」のベクトル(768次元)
[ 0.1, -0.3, 0.8, ...], # 「は」のベクトル
[ 0.3, 0.2, -0.5, ...], # 「学校」のベクトル
[-0.1, 0.4, 0.2, ...]] # 「へ」のベクトル
出力形状: (4, 768) = (系列長, モデル次元)位置エンコーディング(Positional Encoding)の計算
位置エンコーディングとは?
Transformerは各トークンを「同時に」処理するため、トークンの順序情報 をモデルに明示的に与える必要があります。
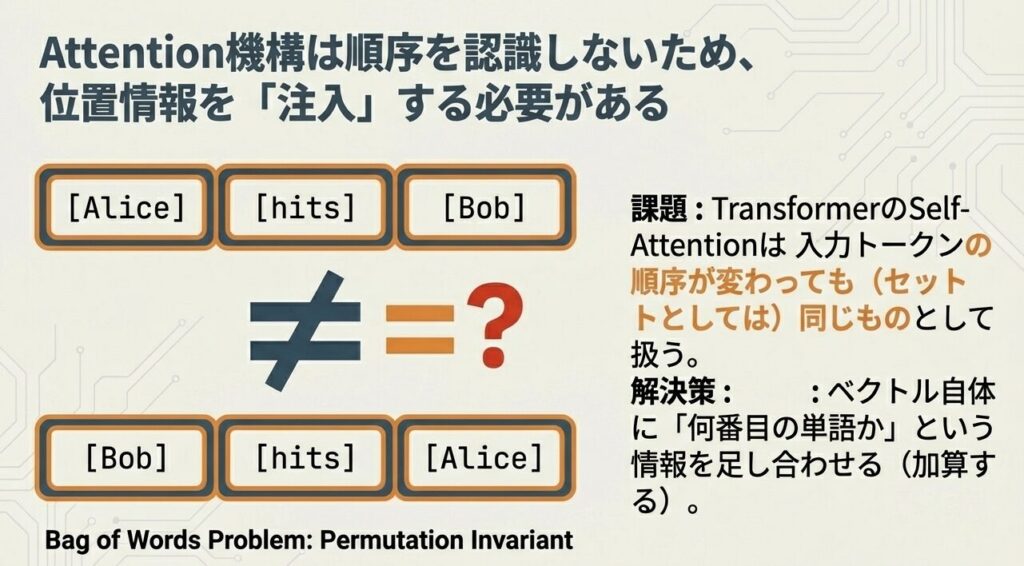
【位置エンコーディングの詳細】

Sinusoidal Positional Encoding の数式

| 記号 | 意味 | 例 |
|---|---|---|
| pos | トークンの位置 | 0, 1, 2, … |
| i | ベクトル次元のインデックス | 0, 1, 2, … |
| dmodel | モデル次元 | 768 |
具体計算例
位置0、モデル次元768の場合:
$i=0$ (偶数) $$ \begin{aligned} PE[0,0] &= \sin\left(\frac{0}{10000^{0/768}}\right) = \sin(0) = 0 \\ PE[0,1] &= \cos\left(\frac{0}{10000^{0/768}}\right) = \cos(0) = 1 \end{aligned} $$
$i=1$ (奇数) $$ \begin{aligned} PE[0,2] &= \sin\left(\frac{0}{10000^{2/768}}\right) = \sin(0) = 0 \\ PE[0,3] &= \cos\left(\frac{0}{10000^{2/768}}\right) = \cos(0) = 1 \end{aligned} $$
位置1の場合:
$i=0$ $$ \begin{aligned} PE[1,0] &= \sin\left(\frac{1}{10000^0}\right) = \sin(1) \approx 0.841 \\ PE[1,1] &= \cos\left(\frac{1}{10000^0}\right) = \cos(1) \approx 0.540 \end{aligned} $$
$i=100$ $$ PE[1,200] = \sin\left(\frac{1}{10000^{200/768}}\right) \approx \dots $$
位置エンコーディングの可視化
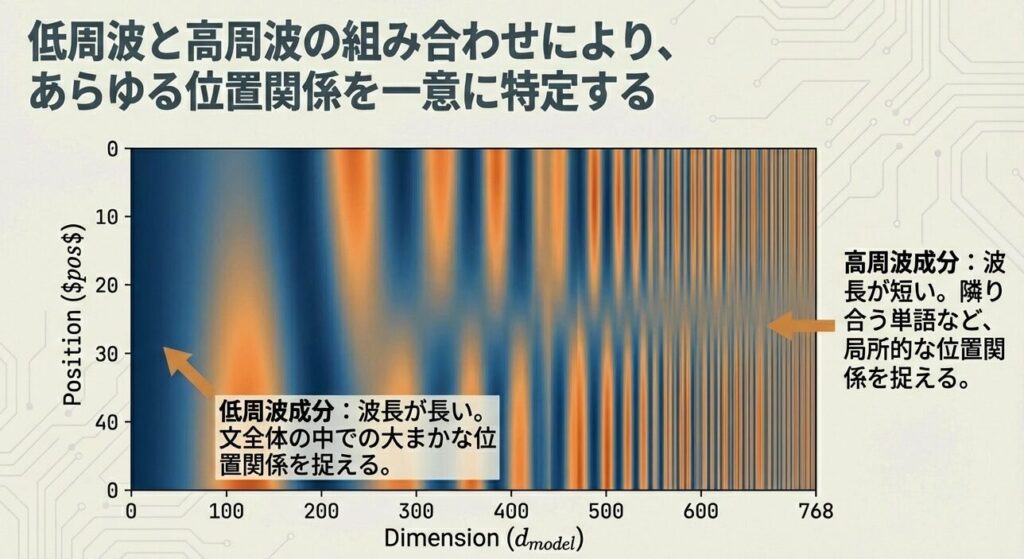
次元 0 次元 1 次元 2 ...
位置0: [0, 1, 0, ...]
位置1: [0.841, 0.540, 0.032, ...]
位置2: [0.909, -0.416, 0.063, ...]
位置3: [0.141, -0.990, 0.095, ...]💡 ポイント
- 低周波成分(次元0-100):位置の大きな変化を捉える
- 高周波成分(次元600-768):位置の細かい変化を捉える
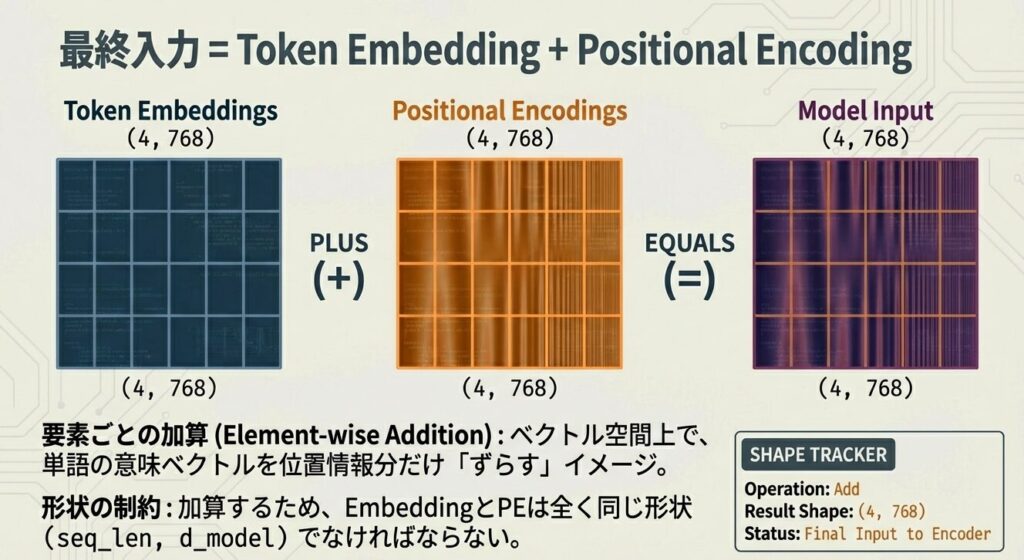
Embedding + Positional Encoding の統合
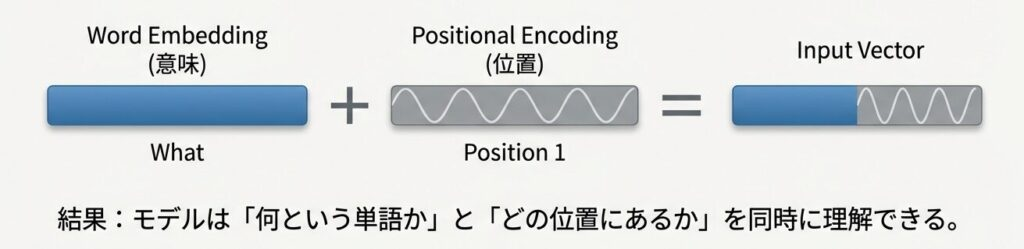
処理フロー
ステップ1:トークン化
入力文 → トークンID列
ステップ2:Embeddingベクトル化
[1050, 80, 2450, 94] → [v_1, v_2, v_3, v_4]
(各v_iは768次元)
ステップ3:位置エンコーディング計算
PE_0, PE_1, PE_2, PE_3(各768次元)
ステップ4:統合(加算)
最終入力 = [v_1 + PE_0,
v_2 + PE_1,
v_3 + PE_2,
v_4 + PE_3]形状の追跡
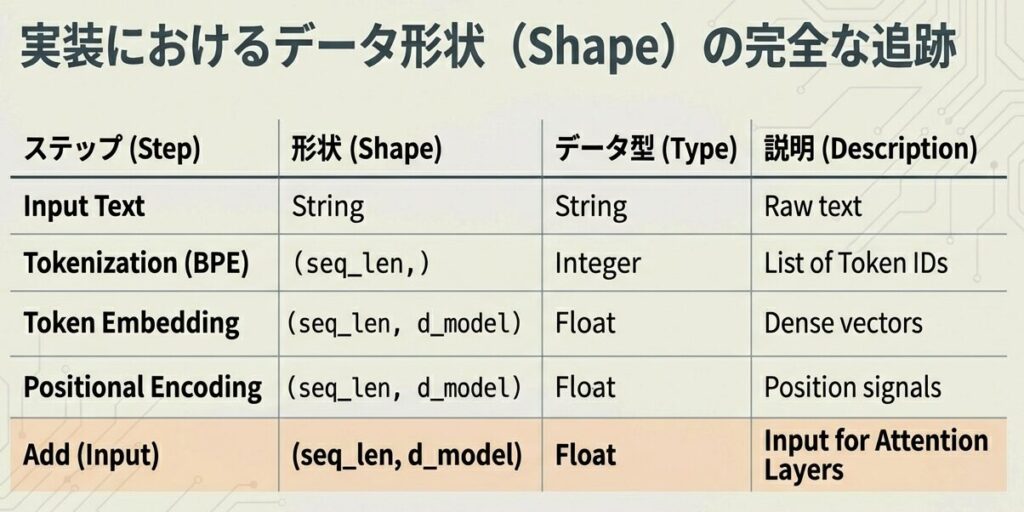
| ステップ | 形状 | 説明 |
|---|---|---|
| トークンID | (4,) | 整数の列 |
| Embedding後 | (4, 768) | 浮動小数点行列 |
| PE | (4, 768) | 位置エンコーディング |
| 統合後 | (4, 768) | 最終入力 |
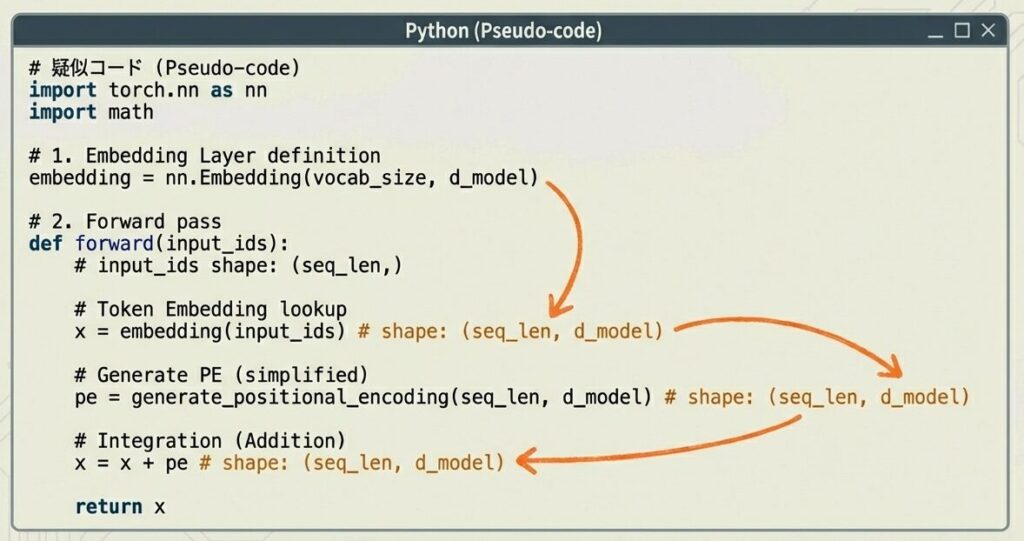
実装例:PyTorch疑似コード
このコードは、Transformer モデルの入力層を実装しています。
具体的には:
- トークン ID → ベクトル変換:語彙内の各トークンを固定次元のベクトル(d_model)に変換
- 位置情報の追加:sin/cos 関数を用いた位置エンコーディングを計算し、トークンの位置情報をベクトルに付与
- 統合:トークン埋め込みと位置エンコーディングを加算し、最終的な入力表現
(batch_size, seq_len, d_model)を出力
つまり、事前学習の全体像としては、テキストのトークン列をニューラルネットワークが処理できる形式に変換するための前処理層が行なっている工程です。
import torch
import torch.nn as nn
import math
class TransformerEmbedding(nn.Module):
def __init__(self, vocab_size, d_model, max_len=5000):
super().__init__()
self.token_embedding = nn.Embedding(vocab_size, d_model)
self.position_encoding = self._create_pe(max_len, d_model)
self.d_model = d_model
def _create_pe(self, max_len, d_model):
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(
torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model)
)
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
return pe.unsqueeze(0) # (1, max_len, d_model)
def forward(self, x):
# x: (batch_size, seq_len) のトークンID
seq_len = x.size(1)
# トークンEmbedding
token_emb = self.token_embedding(x) # (batch, seq_len, d_model)
# スケーリング(オリジナル論文の設定)
token_emb = token_emb * math.sqrt(self.d_model)
# 位置エンコーディングを加算
output = token_emb + self.position_encoding[:, :seq_len, :]
return output # (batch, seq_len, d_model)まとめ
この記事では、Embedding層の実装詳細を解説しました:
| コンポーネント | 役割 | 出力形状 |
|---|---|---|
| BPE | テキスト → トークンID | (seq_len,) |
| Token Embedding | トークンID → ベクトル | (seq_len, d_model) |
| Positional Encoding | 位置情報の追加 | (seq_len, d_model) |
| 統合 | 加算 | (seq_len, d_model) |
次回は、Multi-Head Attentionの詳細アルゴリズムを実装レベルで解説します。
📖 参考文献
主要論文
- Mikolov, T., et al. (2013): “Efficient Estimation of Word Representations in Vector Space”, ICLR 2013
- Sennrich, R., Haddow, B., & Birch, A. (2016): “Neural Machine Translation of Rare Words with Subword Units”, ACL 2016
- Kudo, T., & Richardson, J. (2018): “SentencePiece: A simple and language agnostic approach to subword segmentation”, ACL 2018
📚 シリーズ案内
この記事は「LLM事前学習シリーズ」の一部です。
次に読む
- B-2: Multi-Head Attentionの詳細アルゴリズム – Attention計算の実装


コメント