大規模言語モデル入門【Transformer：実装詳細B-2】

実装詳細

Multi-Head Attentionの詳細アルゴリズム：行列演算の完全追跡

前回はEmbedding層の実装を学びました。今回は、Transformerの心臓部であるMulti-Head Attentionの計算フローを、行列形状とともに完全に追跡します。

Scaled Dot-ProductAttentionの各ステップ、ヘッドの分割と統合プロセスを実装レベルで解説します。大規模言語モデル入門【Transformer：基礎理論A-3】を確認しながら取り組んでみてください。

Scaled Dot-Product Attention の完全な計算フロー

Scaled Dot-Product Attentionとは、Attentionメカニズムの具体的な計算アルゴリズムであり、入力シーケンス内の単語間の関連性を動的に計算する仕組みです。

【Scaled Dot-Product Attentionの詳細】

大規模言語モデル入門【Transformer：基礎理論A-3】
Multi-Head Attentionの詳細メカニズム：文脈理解の核心前回は、Transformerの全体構造を学びました。今回は、その心臓部であるAttentionメカニズムを詳しく解説します。以前のブログでもTransformerにつ...
shion.blog
2026.01.22
【第10回】時系列データ解析と自然言語処理の基礎（後編）
【今回の主な内容】時系列データから言語理解まで、Transformerの可能性を探る今回のテーマは自然言語処理、時系列データ解析、音声認識における技術進化の流れと、Transformerモデルの登場が果たした革新について解説します。まず、自...
shion.blog
2025.02.15

入力の形状

Query (Q):   (batch, seq_len, d_model) = (32, 100, 768)
Key (K):     (batch, seq_len, d_model) = (32, 100, 768)
Value (V):   (batch, seq_len, d_model) = (32, 100, 768)

前提条件と設定パラメータ

パラメータ値説明
batch32バッチサイズ
seq_len100シーケンス長
d_model768モデル次元
num_heads8ヘッド数
d_h96ヘッド次元（768/8）

💡 解説：各次元の意味

（batch=32）：32個のテキスト（文書）を同時に処理しています。バッチ処理により、GPUの計算を効率化します。

（seq_len=100）：各テキストは100個のトークンで構成されています。例えば「I love natural language processing」は5トークンですが、この例では最大100トークンまで処理可能です。

（d_model=768）：各トークンは768次元のベクトルで表現されています。これはGPT-2レベルのモデルの標準的なサイズです。

具体的なイメージ：

バッチ内の1つのテキスト：
  トークン1: [0.1, -0.3, 0.5, ..., 0.2]  （768個の数値）
  トークン2: [0.2, 0.4, -0.1, ..., 0.8]  （768個の数値）
  ...
  トークン100: [0.3, 0.1, 0.6, ..., -0.4] （768個の数値）

これが32個分あるので、合計は 32 × 100 × 768 = 2,457,600個の数値

形状表記の意味：

表記意味
(batch, seq_len, d_model)数学的な一般形。実際の値は状況により変わる
(32, 100, 768)具体例。この場合、バッチサイズ32、シーケンス長100、次元768

💡 形状がなぜ重要か

深層学習では、計算前に形状が正しく一致しているか確認することが重要です。

  • 行列乗算 A @ B では、Aの最後の次元がBの最初の次元と一致する必要があります
  • 形状のミスマッチはエラーの原因になります
  • デバッグ時は形状を追跡することが最も大切です

Q, K, Vが同じ形状である理由：

入力テキスト：「猫は可愛い」（4トークン）

同じ入力から3つのベクトルが生成される：
  Q（クエリ）: [0.1, 0.2, ..., 0.8]  →「この単語の意味を理解したい」
  K（キー）  : [0.3, -0.1, ..., 0.5]  →「この単語の関連情報」
  V（値）    : [0.5, 0.4, ..., 0.2]  →「この単語の実データ」

3つとも同じ形状 (batch, seq_len, d_model) を持ちます

💡 計算効率の観点

Q, K, Vに同じ形状を使うことで、Self-Attention が実現されます。 これにより、トークン間の関係性を双方向で捉えることができます。

ステップ1：Q, K, Vの線形変換（ヘッドごと）

入力埋め込み表現に対し、3つの異なる重み行列を掛けて、Query （Q）， Key （K）， Value （V）を生成します。

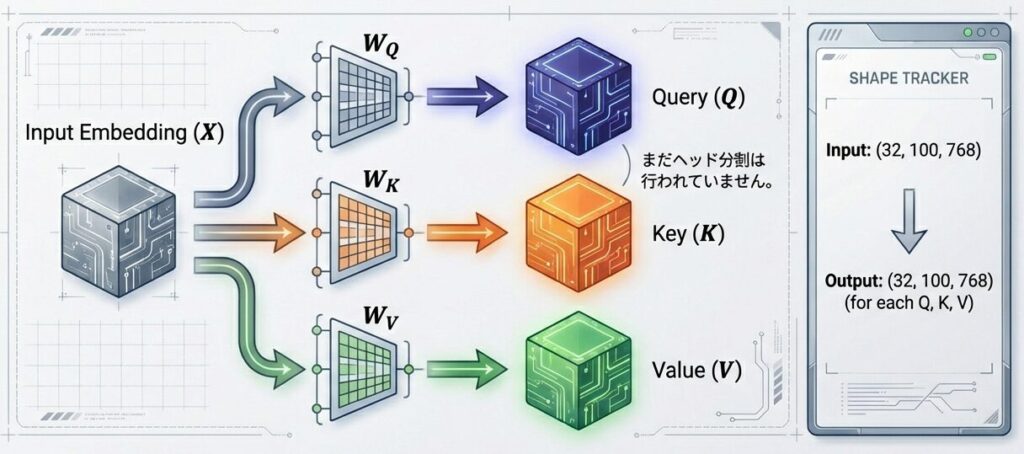
各ヘッド（例：ヘッド0）について：

モデル次元（768）をヘッド数（8）で分割し、ヘッド次元（96）を持つ独立した部分空間を作成します。これにより、8つの独立した「脳」がシーケンスの異なる特徴に同時に注目できるようになります。

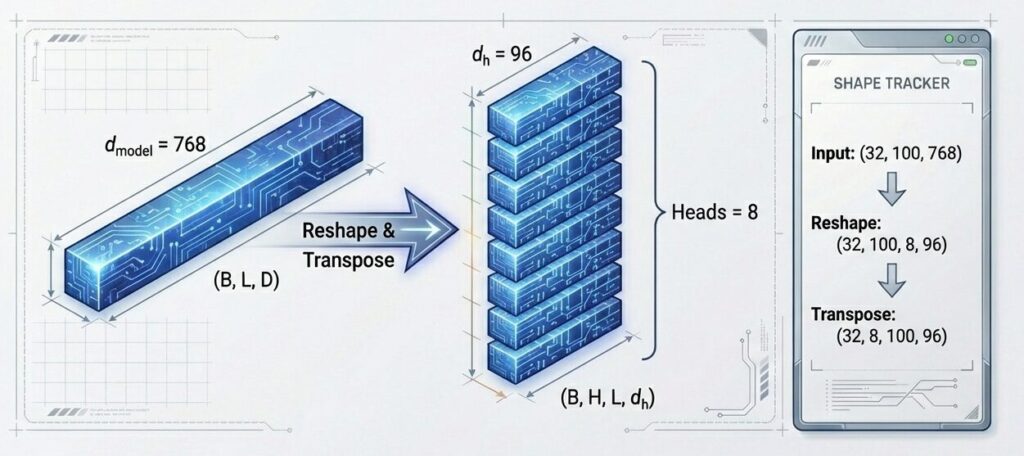
d_h = d_model / num_heads = 768 / 8 = 96

Q_head0 = Input_Q @ W_Q[head0]
        形状：(32, 100, 768) @ (768, 96) = (32, 100, 96)

K_head0 = Input_K @ W_K[head0]
        形状：(32, 100, 768) @ (768, 96) = (32, 100, 96)

V_head0 = Input_V @ W_V[head0]
        形状：(32, 100, 768) @ (768, 96) = (32, 100, 96)

【Q, K, Vの線形変換の詳細】

大規模言語モデル入門【Transformer：基礎理論A-3】
Multi-Head Attentionの詳細メカニズム：文脈理解の核心前回は、Transformerの全体構造を学びました。今回は、その心臓部であるAttentionメカニズムを詳しく解説します。以前のブログでもTransformerにつ...
shion.blog
2026.01.22

ステップ2：スコア計算（行列乗算）

Queryと転置したKeyの内積をとります。これは「100個のトークンx100個のトークン」の関連度を表すマトリクスです。結果の形状の末尾が（100,100）になることに注目。

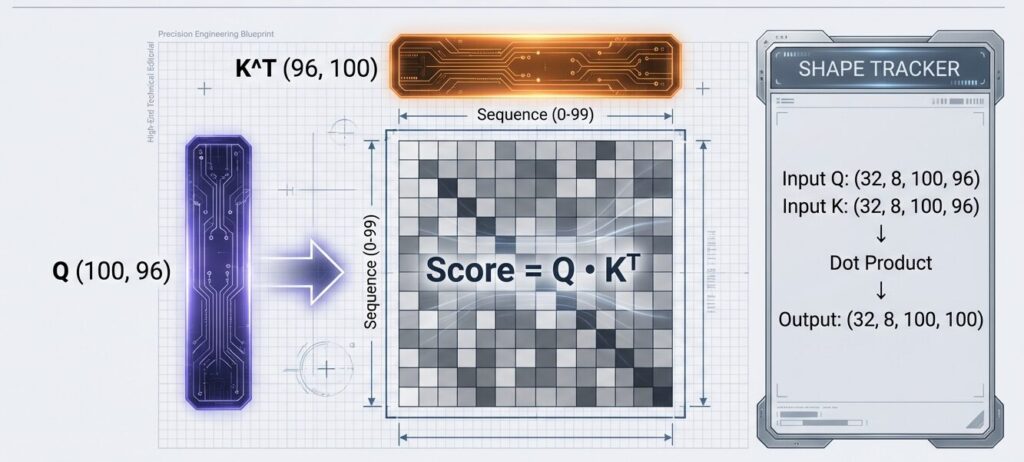
Score_head0 = Q_head0 @ K_head0^T
            形状：(32, 100, 96) @ (32, 96, 100)
                 = (32, 100, 100)

💡 ポイント
これは「100個のトークン × 100個のトークン」の相互注目マトリクスです。

【スコア計算の詳細】

大規模言語モデル入門【Transformer：基礎理論A-3】
Multi-Head Attentionの詳細メカニズム：文脈理解の核心前回は、Transformerの全体構造を学びました。今回は、その心臓部であるAttentionメカニズムを詳しく解説します。以前のブログでもTransformerにつ...
shion.blog
2026.01.22

ステップ3：スケーリング


内積の値を、$\sqrt{d_h}$で割ります。次数が大きくなると内積値が増大し、Softmaxの勾配消失を招くのを防ぐためです。

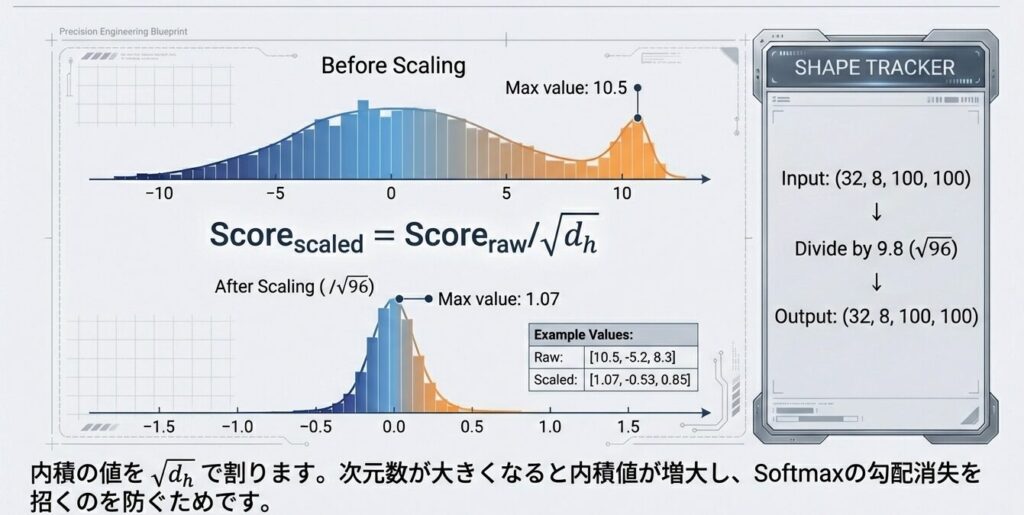
Scaled_Score_head0 = Score_head0 / √(d_h)
                   = Score_head0 / √96
                   = Score_head0 / 9.8

数値例：

状態値の例
スケーリング前[10.5, -5.2, 8.3, …]
スケーリング後[1.07, -0.53, 0.85, …]

【スケーリングの詳細】

大規模言語モデル入門【Transformer：基礎理論A-3】
Multi-Head Attentionの詳細メカニズム：文脈理解の核心前回は、Transformerの全体構造を学びました。今回は、その心臓部であるAttentionメカニズムを詳しく解説します。以前のブログでもTransformerにつ...
shion.blog
2026.01.22

ステップ4：Softmax による正規化

行ごとにSoftmax関数を適用します。これにより、各トークンが「他のどのトークンにどれだけ注目すべきか」が確率（0.0～1.0）として表現されます。各行の合計値は必ず1.0になります。

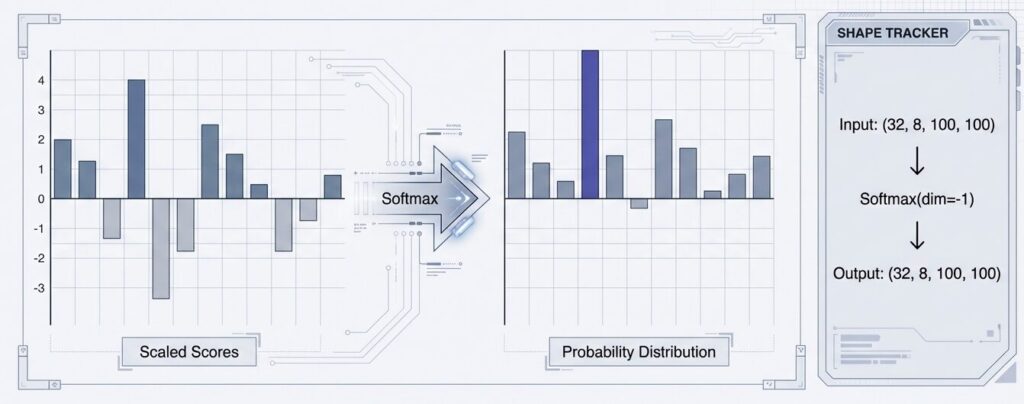
Attention_Weights_head0 = Softmax(Scaled_Score_head0, dim=-1)

結果：各行の合計が1.0になる確率分布

例（5トークンの場合）：[0.35, 0.12, 0.28, 0.15, 0.10]
                      合計 = 1.0

ステップ5：出力計算（加重平均）

算出された確率（Attention Weights）を使って、Valueベクトルの加重平均をとります。関連度の高いトークンの情報は強く、そうでない情報は弱く取り込まれます。

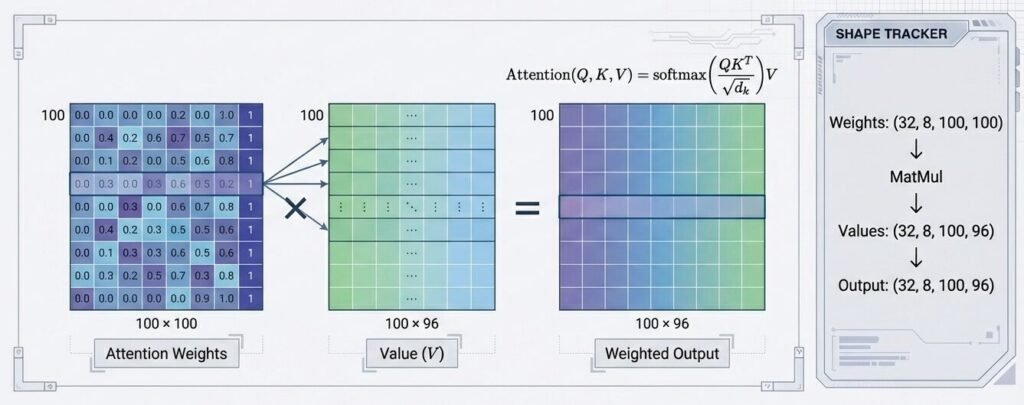
Attention_Output_head0 = Attention_Weights_head0 @ V_head0
                        形状：(32, 100, 100) @ (32, 100, 96)
                             = (32, 100, 96)

意味： 各トークンが、全トークンのValueベクトルをAttention Weightsで重み付けした加重平均

Multi-Head Attentionの全ヘッド統合

8つのヘッドの出力を連結（Concat）し、元のモデル次元d_model （768）の形状に戻します。

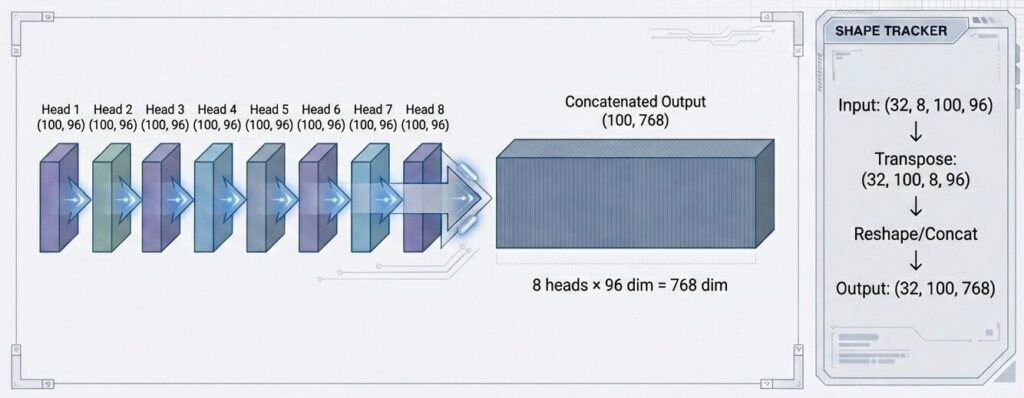
複数ヘッドの並列実行

ヘッド1: (32, 100, 96) → (32, 100, 96)
ヘッド2: (32, 100, 96) → (32, 100, 96)
...
ヘッド8: (32, 100, 96) → (32, 100, 96)

すべて並列で計算（GPUで効率的）

ヘッド出力の連結

Concatenate([head1_output, head2_output, ..., head8_output])

結果：(32, 100, 96×8) = (32, 100, 768)

最終線形変換

連結されたベクトルに、学習可能な重み行列W。を掛けます。これにより、別々のヘッドで収集された情報が相互に混合・統合され、次の層へ渡されます。

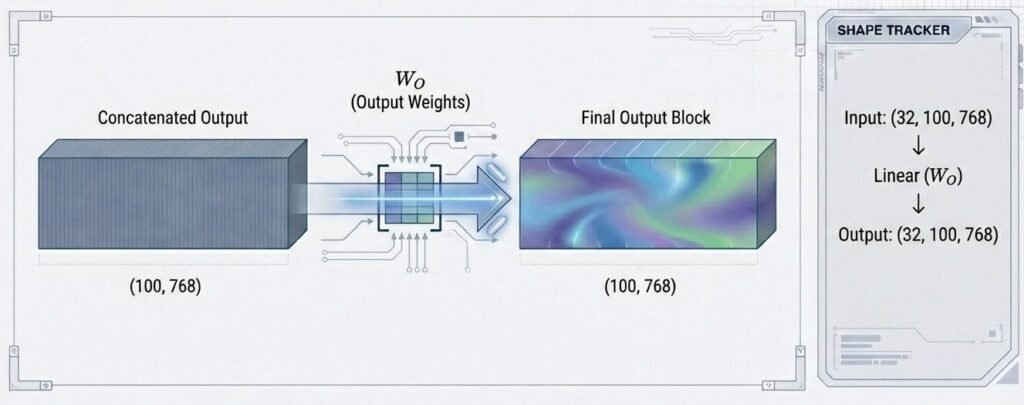
MHA_Output = Concatenated_Outputs @ W_O
           形状：(32, 100, 768) @ (768, 768)
                = (32, 100, 768)

💡 ポイント
W_Oは学習可能な重み行列で、複数ヘッドの情報を統合・圧縮します。

全体の計算グラフ

[入力 (32, 100, 768)]
    ↓ (W_Q, W_K, W_V で分割)
[Q, K, V各(32, 100, 768)]
    ↓ (8ヘッドに分割：各768→96)
[8つのヘッド、各(32, 100, 96)]
    ↓ (並列計算：Scaled Dot-Product Attention)
[8つの出力、各(32, 100, 96)]
    ↓ (連結：8×96 = 768)
[連結結果 (32, 100, 768)]
    ↓ (W_Oで統合)
[MHA出力 (32, 100, 768)]

実装例：PyTorch疑似コード

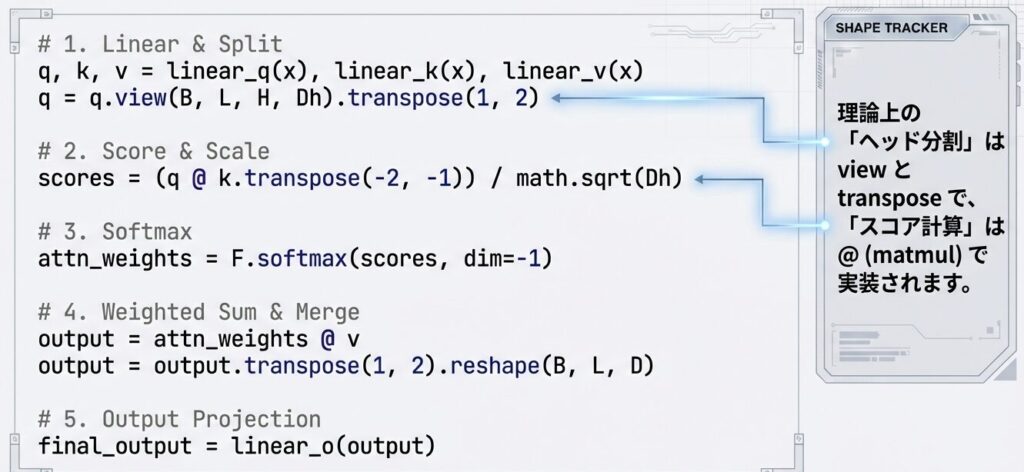
このコードは、Multi-Head Attentionの完全な実装です。

具体的には：

  1. Q, K, V生成：入力を線形変換して Query、Key、Value ベクトルを生成
  2. 複数ヘッドに分割：d_model次元を num_heads 個に分割し、各ヘッドが独立して計算できる形に整形
  3. Scaled Dot-Product Attention：各ヘッドで Q・K内積 → スケーリング → Softmax → 加重平均を実行
  4. ヘッド統合：複数ヘッドの出力を連結
  5. 最終出力変換：W_O で統合ベクトルに変換

結果として、異なる視点から同時に文脈を捉えた、より豊かな表現ベクトルを出力します。

【詳細実装】

import torch
import torch.nn as nn
import math

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.d_h = d_model // num_heads
        
        # Q, K, V の線形変換
        self.W_Q = nn.Linear(d_model, d_model)
        self.W_K = nn.Linear(d_model, d_model)
        self.W_V = nn.Linear(d_model, d_model)
        
        # 出力の線形変換
        self.W_O = nn.Linear(d_model, d_model)
    
    def forward(self, Q, K, V, mask=None):
        batch_size = Q.size(0)
        
        # 1. 線形変換
        Q = self.W_Q(Q)  # (batch, seq, d_model)
        K = self.W_K(K)
        V = self.W_V(V)
        
        # 2. ヘッドに分割
        Q = Q.view(batch_size, -1, self.num_heads, self.d_h).transpose(1, 2)
        K = K.view(batch_size, -1, self.num_heads, self.d_h).transpose(1, 2)
        V = V.view(batch_size, -1, self.num_heads, self.d_h).transpose(1, 2)
        # 形状: (batch, num_heads, seq, d_h)
        
        # 3. Scaled Dot-Product Attention
        scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_h)
        
        if mask is not None:
            scores = scores.masked_fill(mask == 0, -1e9)
        
        attention_weights = torch.softmax(scores, dim=-1)
        attention_output = torch.matmul(attention_weights, V)
        
        # 4. ヘッドを連結
        attention_output = attention_output.transpose(1, 2).contiguous()
        attention_output = attention_output.view(batch_size, -1, self.d_model)
        
        # 5. 最終線形変換
        output = self.W_O(attention_output)
        
        return output

形状変化のまとめ

シーケンス長（n）が増えると、スコア計算と加重平均の計算量が二乗で増加します。

ステップ操作形状
入力–(batch, seq, d_model)
線形変換W_Q, W_K, W_V(batch, seq, d_model)
ヘッド分割reshape + transpose(batch, heads, seq, d_h)
スコア計算$Q @ K^T$(batch, heads, seq, seq)
スケーリング/ √d_h(batch, heads, seq, seq)
Softmaxsoftmax(batch, heads, seq, seq)
加重平均$weights @ V$(batch, heads, seq, d_h)
連結concat(batch, seq, d_model)
出力変換W_O(batch, seq, d_model)

まとめ

この記事では、Multi-Head Attentionの計算フローを完全に追跡しました。

処理計算量特徴
ヘッド分割O(n)並列化可能
スコア計算O(n²d)ボトルネック
SoftmaxO(n²)行ごとに独立
加重平均O(n²d)ボトルネック
連結・統合O(nd²)線形

次回は、Causal Maskingと並列学習の実装を解説します。

📖 参考文献

主要論文

  1. Vaswani, A., et al. (2017): “Attention Is All You Need”, NeurIPS 2017
  2. Dao, T., Fu, D. Y., Ermon, S., Rudra, A., & Ré, C. (2022): “FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness”, NeurIPS 2022
  3. Shazeer, N. (2019): “Fast Transformer Decoding: One Write-Head is All You Need”, arXiv

📚 シリーズ案内

次に読む

コメント

タイトルとURLをコピーしました