前編の目標:データのクラスタリングと分類
データのラベルがない状態でも、クラスタリングによってデータのグループを見つけ、分類する力を養います。K-meansや階層型クラスタリングといった手法を通じて、データをどのように分割・構造化できるかを学び、以下の成果を目指します。
- グループの発見: データ間の類似性や共通性を見つけ、データをクラスター化できる。
- クラスタリングの数式的理解:各アルゴリズムの数式やメカニズムを理解し、数学的に説明できるようにする。
- 実践的な応用:K-meansや階層型クラスタリングを用いて、顧客セグメンテーションやデータグルーピングに応用する。
クラスタリング手法
クラスタリングは、教師なし学習の中でも特に重要な分野で、データ間のパターンを探すための基本的な手法です。各手法の強みや弱みを理解し、どのようなデータセットに適用するのが効果的かを判断することが求められます。また、K-meansではエルボー法を用いた最適なクラスタ数の決定、階層型クラスタリングではデンドログラムによるクラスタの視覚化が重要です。
K-平均法 (K-means Clustering)
K-平均法は、データを事前に指定した$K$個のクラスタに分割するクラスタリング手法です。各クラスタの中心点(重心)見つけるために繰り返し計算し、データ間の類似性を反映します。
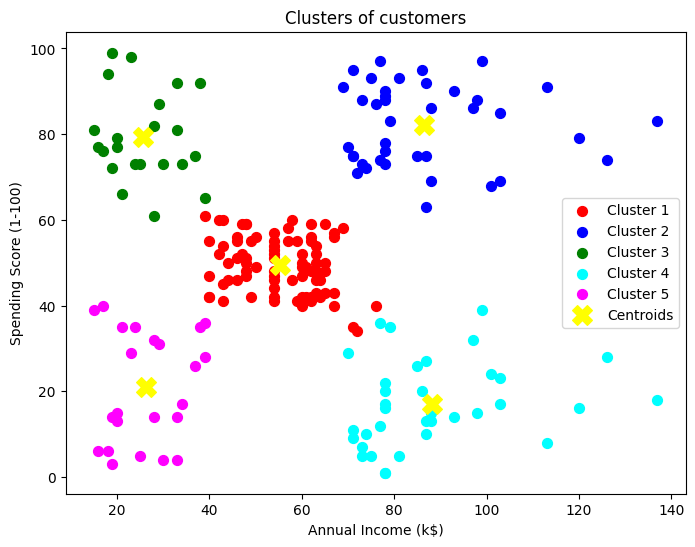
図はK=5のクラスタリングで各々5分類の色分けの中心である黄色の×印が各クラスタの中心点(重心)です。これは既に学習が終わって描画したグラフですが、この描画に至るまでに反復計算を繰り返しています。
クラスタリングの手順
初期設定
- データの中から、クラスタの中心点(重心)となる位置をランダムに $K$ 個選びます。

データの割り当て
- 各データ点に対して、最も近い中心点(重心)を探し、そのクラスタに割り当てます。
- ここでコサイン類似度という指標を使うことができます。コサイン類似度についてはもう少し先でお話しします。

距離の計算:
データ点$x_i$と重心$\mu_j$との距離は通常、ユークリッド距離で計算します。
$$d(x_i, \mu_j) = \sum_{l=1}^{n} (x_{il} – \mu_{jl})^2$$
- $n$は特徴量の数です。
新しい中心点の計算
- 割り当てられたデータ点を基に、各クラスタの重心を再計算し、新たな中心点(重心)とします。

目的関数(損失関数):
K-平均法は、以下の目的関数を最小化することを目指します。
$$J = \sum_{j=1}^{K} \sum_{x_i \in C_j} \|x_i – \mu_j\|^2$$
- $C_j$:クラスタ
- $j$に属するデータ点の集合
- $\mu_j$:クラスタ$j$の重心
繰り返し処理
- 手順2と手順3を繰り返し、データ点の割り当てが変わらなくなるまで続けます。
- 注: 繰り返しの回数が設定された上限 $N$ に達した場合、その時点で処理を終了します。
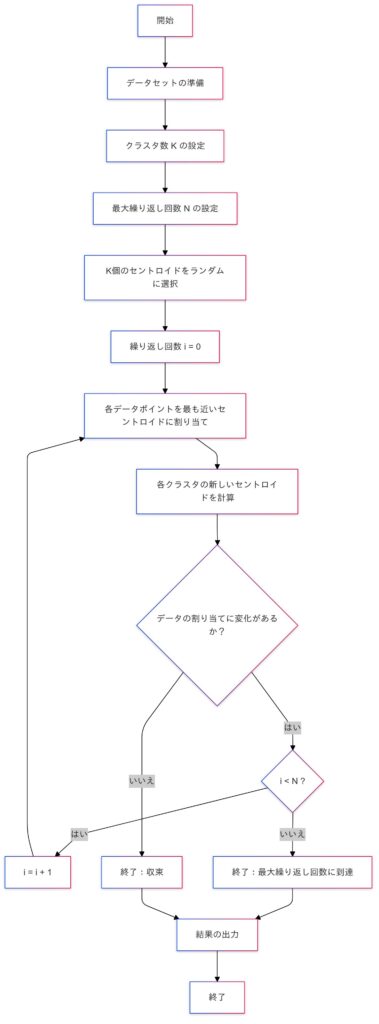
クラスタリングの手順をフローチャートで説明
クラスタリングの特徴
| 特徴 | 説明 |
|---|---|
| ラベルなしデータからパターンを発見 | クラスタリングはラベルのないデータに適用され、データの自然なグループを発見します。 |
| クラスタ数 ( K ) の指定 | ユーザーがクラスタ数 ( K ) を事前に指定し、それに基づいてデータを ( K ) 個のグループに分類。 |
| データ間の類似性に基づく分類 | 各データ点が最も近いクラスタの重心に割り当てられ、データ点間の類似性(距離)をもとに分類します。 |
| 反復的な最適化プロセス | クラスタの重心とデータ点の割り当てが繰り返し更新され、誤差が最小化されるまで反復します。 |
| 中心点の更新による収束性 | 各クラスタの重心が反復的に更新され、一定の条件でクラスタが安定(収束)します。 |
| 効率性とスケーラビリティ | K-means法は計算コストが比較的低く、大規模データにも適していますが、クラスタ数が多すぎると負荷増。 |
| クラスタの形状に依存 | 球状のクラスタに適していますが、非球状や密度が異なるデータには適しません。 |
| エルボー法やシルエットスコアでの最適クラスタ数 | エルボー法やシルエットスコアを用いて、データの構造に適したクラスタ数を推定します。 |
K-means++
K-meansの問題点
K-meansには初期値によって結果が大きく変わってしまうことがあるという問題点があります。
特に、悪い初期値を選んでしまうと、収束が遅くなったり、局所最適解に陥ったりする可能性があり注意が必要です。そんな背景からK-means++は開発されました。
K-means++とは?
最初の中心点をランダムに選んだ後、次の中心点は既存の中心点からの距離が最大になるように選ばれます。この方法により、初期中心点がより均等に分布し、収束が早く、結果が改善されることが期待されます。
K-means++の実装
K-means++の実装はscikitlearnのK-meansのデフォルトで実装可能です。
データセットについて
顧客セグメンテーションのデータセットを使ってクラスタリングのアルゴリズムであるK-means法の説明をします。
このデータセットは自分がスーパーマーケットモールを経営しており、会員カードを通じて顧客 ID、年齢、性別、年収、支出スコアなどの顧客に関する基本データを持っています。
支出スコアは、顧客の行動や購入データなどの定義したパラメータに基づいて顧客に割り当てるものです。
問題の説明
あなたはショッピングモールを所有しており、簡単に収束できる顧客(ターゲット顧客)を理解して、マーケティングチームにその意味を伝え、それに応じて戦略を計画したいと考えています。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeansデータの読み込み、 Mall_Customers.csv からデータを読み込み、ショッピングモールの年収と支出スコアを特徴量として選択します。
# データの読み込み
data = pd.read_csv('Mall_Customers.csv')
# 必要な特徴量の選択
X = data[['Annual Income (k$)', 'Spending Score (1-100)']].values最適なクラスタ数の決定(エルボー法):
wcss = []
for k in range(1, 11):
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(X)
wcss.append(kmeans.inertia_) # クラスタにおける慣性を表すkmeans.inertia_ は、K-meansクラスタリングにおける慣性を表し、クラスタ内のデータポイントとそのクラスタ中心との距離の合計を示します。
# エルボー法のプロット
plt.figure(figsize=(8, 4))
plt.plot(range(1, 11), wcss, marker='o')
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('Within-cluster Sum of Squares')
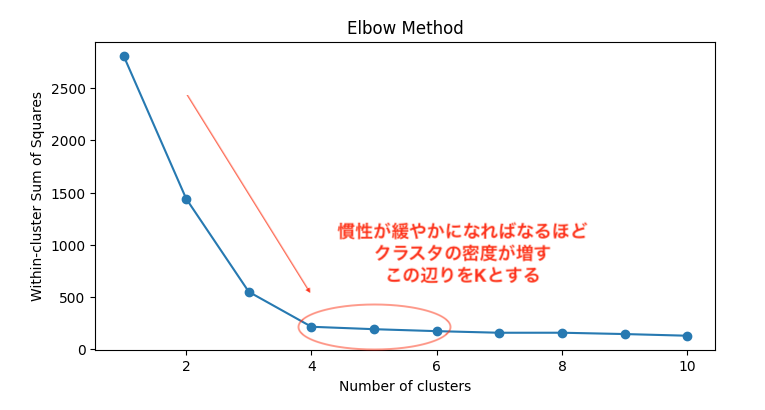
plt.show()慣性とは?:
慣性が小さいほど、データポイントがクラスタ中心に近いことを示し、クラスタが密集していることを意味します。逆に、慣性が大きい場合は、データポイントがクラスタ中心から遠く離れていることを示し、クラスタが散らばっていることを意味します。
# 最適なクラスタ数を5と仮定
kmeans = KMeans(n_clusters=5, random_state=42)
y_kmeans = kmeans.fit_predict(X)# クラスタの可視化
plt.figure(figsize=(8, 6))
colors = ['red', 'blue', 'green', 'cyan', 'magenta']
labels = ['Cluster 1', 'Cluster 2', 'Cluster 3', 'Cluster 4', 'Cluster 5']
for i in range(5):
plt.scatter(X[y_kmeans == i, 0], X[y_kmeans == i, 1],
s=50, c=colors[i], label=labels[i])
# 重心のプロット
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
s=200, c='yellow', label='Centroids', marker='X')
plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()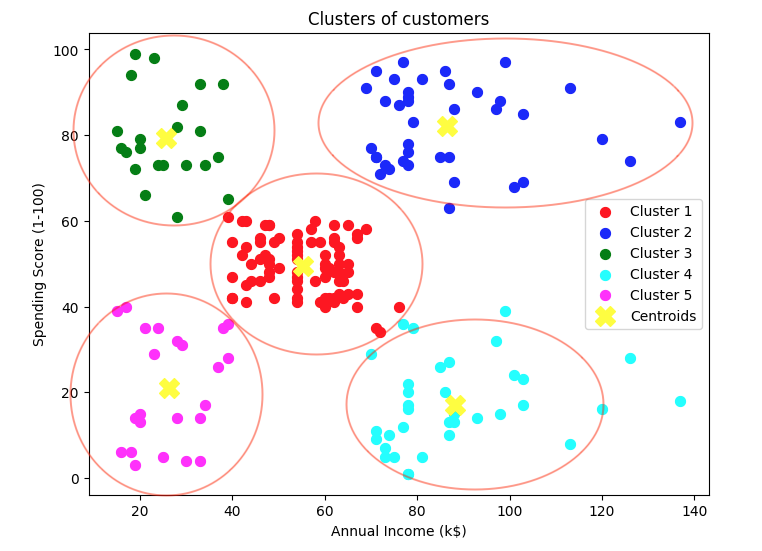
クラスタの集合と重心から読み取れるデータを参考に顧客データによるマーケティングや経営の改善計画を考えることができます。以下はその参考事例です。
| 改善項目 | 内容 |
|---|---|
| ターゲットマーケティングの強化 | 各セグメントに合わせたプロモーションを実施し、効果的にマーケティングを行います。 |
| 商品配置と在庫管理の最適化 | 各顧客層が好む商品を分析し、店舗内の商品配置を改善して購買意欲を向上させます。 |
| 顧客体験の向上 | パーソナライズされたサービスを提供し、顧客満足度を高めます。 |
| 新規顧客の獲得 | ターゲット広告を活用し、特定の顧客層に効果的にアプローチして新規顧客を増やします。 |
| 顧客ロイヤルティプログラムの導入 | 各セグメントに合わせたロイヤルティプログラムを設計し、リピート購入を促進します。 |
| データの継続的な分析 | 顧客データを定期的に更新し、常に最新のセグメントに基づいた戦略を維持します。 |
K-meansの実装
先ほどはK-meansよりも精度の良いK-means++の実装を行いましたが、ここでは一応、K-meansの実装についても触れておきます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# K-meansアルゴリズムの実装
class KMeansManual:
def __init__(self, n_clusters=3, max_iter=100, tol=1e-4):
self.n_clusters = n_clusters
self.max_iter = max_iter
self.tol = tol
self.centroids = None
def fit(self, X):
# ランダムに初期クラスタ中心を選択
random_indices = np.random.choice(X.shape[0], self.n_clusters, replace=False)
self.centroids = X[random_indices]
for _ in range(self.max_iter):
# 各データポイントに最も近いクラスタ中心を割り当てる
distances = self._compute_distances(X)
labels = np.argmin(distances, axis=1)
# 新しいクラスタ中心を計算
new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(self.n_clusters)])
# 中心の変化を確認
if np.all(np.abs(new_centroids - self.centroids) < self.tol):
break
self.centroids = new_centroids
return labels
def _compute_distances(self, X):
# 各データポイントとクラスタ中心との距離を計算
return np.linalg.norm(X[:, np.newaxis] - self.centroids, axis=2)
# データの読み込み
data = pd.read_csv('Mall_Customers.csv')
# 必要な特徴量の選択
X = data[['Annual Income (k$)', 'Spending Score (1-100)']].values
# エルボー法の実行
wcss = []
for k in range(1, 11):
kmeans = KMeansManual(n_clusters=k)
kmeans.fit(X)
# 各クラスタの慣性を計算
distances = kmeans._compute_distances(X)
inertia = np.sum(np.min(distances, axis=1)**2)
wcss.append(inertia)
# エルボー法のプロット
plt.figure(figsize=(8, 4))
plt.plot(range(1, 11), wcss, marker='o')
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('Within-cluster Sum of Squares')
plt.show()
# 最適なクラスタ数を5と仮定
kmeans = KMeansManual(n_clusters=5)
y_kmeans = kmeans.fit(X)
# クラスタの可視化
plt.figure(figsize=(8, 6))
colors = ['red', 'blue', 'green', 'cyan', 'magenta']
labels = ['Cluster 1', 'Cluster 2', 'Cluster 3', 'Cluster 4', 'Cluster 5']
for i in range(5):
plt.scatter(X[y_kmeans == i, 0], X[y_kmeans == i, 1],
s=50, c=colors[i], label=labels[i])
# 重心のプロット
plt.scatter(kmeans.centroids[:, 0], kmeans.centroids[:, 1],
s=200, c='yellow', label='Centroids', marker='X')
plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()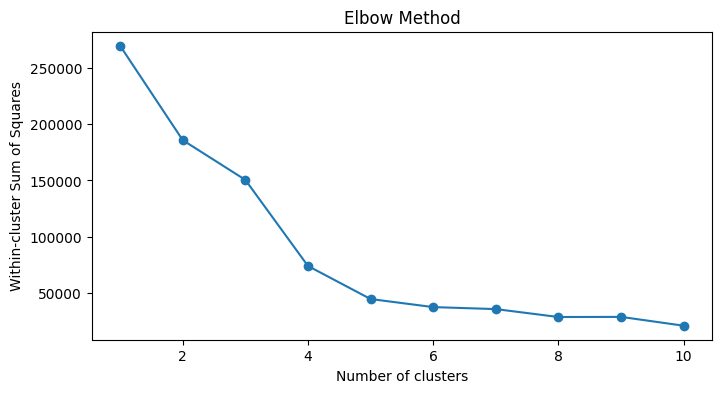
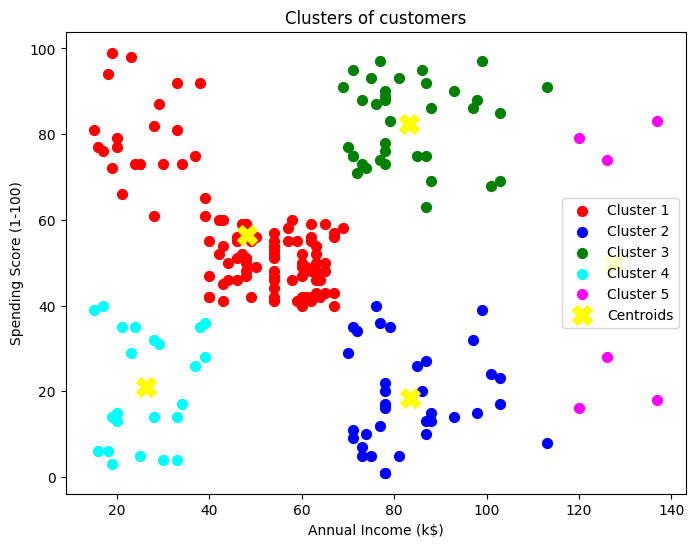
クラスタリングの精度はやはりK-means++の方が上です。
コサイン類似度
コサイン類似度は、2つのベクトルがどれだけ同じ方向を向いているかを測る方法です。具体的には、ベクトルの内積(角度のコサイン値)を使って計算します。この値は -1 から 1 の範囲を取り、以下のように解釈します。
| コサイン類似度の値 | 解釈 |
|---|---|
| 1 に近い | 顧客の年収と支出スコアが非常に似ており、類似した購買行動を持っている可能性が高い。 |
| 0 に近い | 顧客の年収と支出スコアにほとんど関係がなく、異なる購買行動を持っている可能性が高い。 |
| -1 に近い | 顧客の年収と支出スコアが正反対の傾向にあることを示し、通常は稀だが、特定の条件下で発生する可能性がある。 |
コサイン類似度を使用することで、顧客間の類似性を分析し、マーケティング戦略やサービスの向上に役立てることができます。K-meansクラスタリングと組み合わせることで、より詳細な顧客セグメンテーションや推薦システムの構築が可能になります。
$$\text{コサイン類似度} = \frac{x \cdot y}{|x| |y|} = \frac{\sum_{i=1}^{n} x_i y_i}{\sqrt{\sum_{i=1}^{n} x_i^2 \cdot \sum_{i=1}^{n} y_i^2}}$$
- $x$ と $y$ は2つのベクトル。
- $x$・$y$ は2つのベクトルの内積で、対応する要素同士を掛け合わせたものの合計です。
- $|x|$ と $|y|$ は、それぞれのベクトルの大きさ(ノルム)で、要素の二乗和の平方根です。
K-meansとコサイン類似度の違い
- K-means:データを複数のクラスタに分類し、重心ごとの特徴を明らかにするために使われるクラスタリング手法です。
- コサイン類似度:データ間の向き(類似性)を角度で測り、2つのデータがどれだけ似ているかを評価するための指標です。
コサイン類似度の実装
先ほどと同じデータを使って実装を行います。
from sklearn.metrics.pairwise import cosine_similarity
import seaborn as sns
# データの読み込み
data = pd.read_csv('Mall_Customers.csv')
# 必要な特徴量の選択
X = data[['Annual Income (k$)', 'Spending Score (1-100)']].values
# コサイン類似度の計算
cosine_sim = cosine_similarity(X)
# コサイン類似度行列の表示
print("Cosine Similarity Matrix (scikit-learn):")
print(cosine_sim)
# コサイン類似度行列の可視化
plt.figure(figsize=(10, 8))
sns.heatmap(cosine_sim, cmap='viridis', square=True, cbar=True, annot=False)
plt.title('Cosine Similarity Matrix')
plt.xlabel('Customers')
plt.ylabel('Customers')
plt.show()Cosine Similarity Matrix (scikit-learn):
[[1. 0.98310817 0.66384211 ... 0.7822092 0.4775046 0.79065371]
[0.98310817 1. 0.51574885 ... 0.65496849 0.30862716 0.66523831]
[0.66384211 0.51574885 1. ... 0.9852 0.97409054 0.98276449]
...
[0.7822092 0.65496849 0.9852 ... 1. 0.92090845 0.99990654]
[0.4775046 0.30862716 0.97409054 ... 0.92090845 1. 0.91549348]
[0.79065371 0.66523831 0.98276449 ... 0.99990654 0.91549348 1. ]]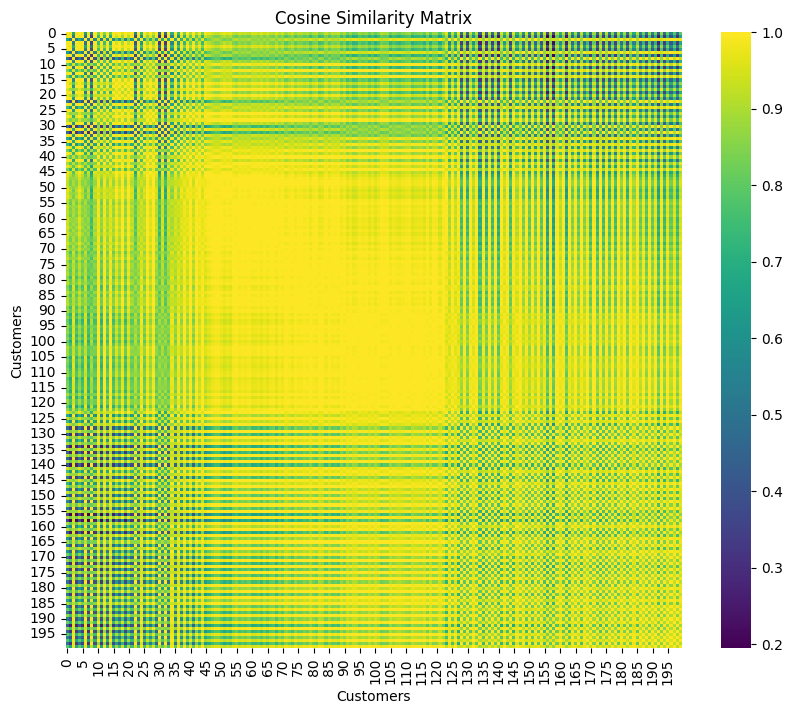
ベクトルの内積によって算出されたコサイン類似度によって顧客間の類似度をヒートマップによって可視化することができます。以下にヒートマップから導き出せる事柄をまとめてみました。
| 分析項目 | 説明 |
|---|---|
| 顧客間の類似性 | ヒートマップの色の濃さが顧客間の類似度の強さを示し、色が濃いほど類似度が高く、顧客間の特徴(年収や支出スコア)が似ていることを意味します。 |
| クラスタの特定 | ヒートマップで特定の行や列が似ている場合、同様の購買行動や嗜好を持つ顧客グループが視覚的に確認できます。 |
| マーケティング戦略の策定 | 類似した顧客をグループ化し、特定のクラスタに属する顧客に対して、ターゲットを絞ったプロモーションやキャンペーンを実施します。 |
| 異常値の検出 | ヒートマップで色が薄い顧客を見つけることで、異常な購買行動や嗜好を持つ顧客を特定し、特別な対応が必要な顧客を見つけられます。 |
| データの全体的な傾向 | ヒートマップを通じて、顧客群間の全体的な傾向やパターンを把握し、どの顧客群が似ているか、または異なるかを視覚的に理解できます。 |
階層型クラスタリング (Hierarchical Clustering)
階層クラスタリングは、データを階層的にグループ化するクラスタリング手法です。クラスタ間の関係を「デンドログラム」という樹形図で視覚化できる点が特徴で、データ間の類似度に応じたグループ化を視覚的に理解するのに役立ちます。
階層型クラスタリングには主に以下の2種類があります。
- 凝集型(Agglomerative): 各データ点を個別のクラスタとし、近いクラスタ同士を逐次結合していくボトムアップ方式。
- 分割型(Divisive): データ全体を1つのクラスタとみなし、類似度の低い部分から逐次分割していくトップダウン方式。
本記事では一般的に使用される「凝集型(Agglomerative)」に焦点を当てます。
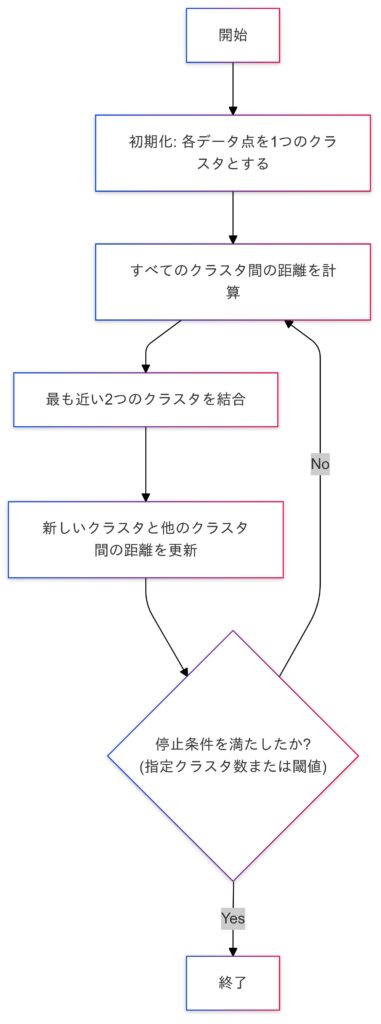
階層型クラスタリングの手順
- 初期化:各データ点を一つのクラスタとする。
- 距離の計算:すべてのクラスタ間の距離(類似度)を計算する。
- クラスタの結合:最も近い(類似度が高い)二つのクラスタを結合する。
- 距離の更新:新たに形成されたクラスタと他のクラスタ間の距離を再計算する。
- 停止条件の判定:クラスタ数が指定の数になるまで、または一定の条件を満たすまで2から4の手順を繰り返す。
デンドログラムの役割
デンドログラムは階層クラスタリングの結果を視覚化するためのツールで、データがどのようにグループ化されていくか、クラスタ間の距離がどの程度かを示します。分岐の高さはクラスタ間の距離を示し、特定の高さで分割することで、最適なクラスタ数(K)を決定する手がかりになります。
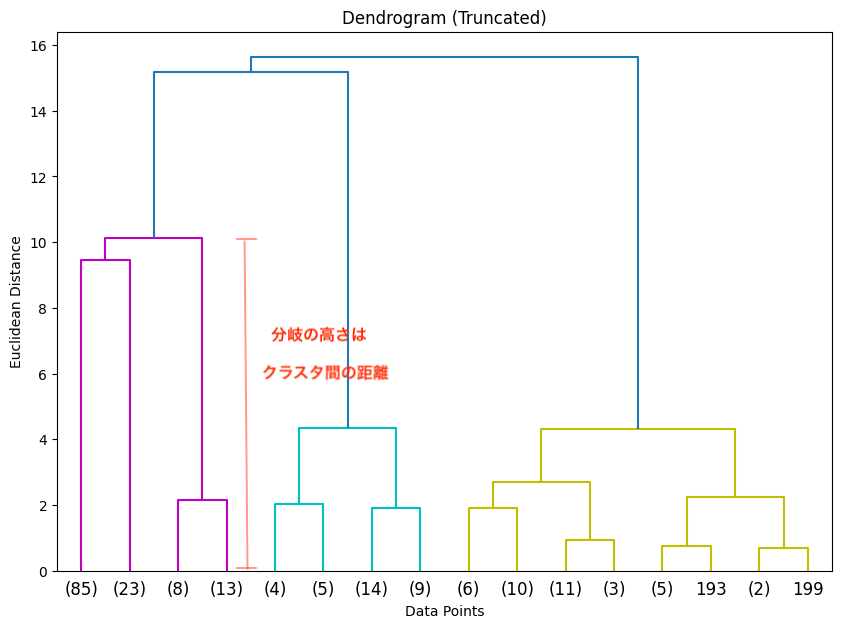
今回の図では、約10〜12あたりの高さで大きく分岐しているのがわかります。この高さに水平線を引くと、左、中、右の3つの大きなクラスタに分割されます。故にK=3となります。
距離(類似度)の計算方法
類似度の計算方法によって可視化されるクラスタリングのグラフが変わってきます。
距離(類似度)計算方法の違いにより、階層クラスタリングの結果が変わる理由は、データのグループ化に対する「捉え方」が異なるためです。たとえば、単一リンク法は「連続性」を重視してつながりを重視するのに対し、完全リンク法は「密度」を重視して、よりコンパクトなクラスタを形成します。
適切な計算方法を選ぶことで、データの本質に沿ったグループ化が可能になり、得られるインサイトがより的確になります。
Single(単一リンク法)
二つのクラスタ間の最近接点の距離をクラスタ間距離とする。
$$d(A, B) = \min_{a \in A, b \in B} d(a, b)$$
Complete(完全リンク法)
二つのクラスタ間の最遠点の距離をクラスタ間距離とする。
$$d(A, B) = \max_{a \in A, b \in B} d(a, b)$$
Average(平均リンク法)
二つのクラスタ間の全ての点の距離の平均をクラスタ間距離とする。
$$d(A, B) = \frac{1}{|A||B|} \sum_{a \in A} \sum_{b \in B} d(a, b)$$
Ward(ウォード法)
クラスタ内の分散の増加を最小化するようにクラスタを結合する。計算量が多いが精度が良いためよく使われる。
$$d(A, B) = \frac{n_A + n_B}{n_A n_B} \| \bar{x}_A – \bar{x}_B \|^2$$
- $n_A$ および $n_B$ : クラスタ $A$ とクラスタ $B$ のデータ点数
- $\bar{x}_A$ および $\bar{x}_B$ : クラスタ $A$ とクラスタ $B$ の重心(平均ベクトル)
- $| \bar{x}_A – \bar{x}_B |^2$ : クラスタの重心間のユークリッド距離の2乗。
階層クラスタリングの実装
先ほどと同じ顧客セグメンテーションのデータセットを使って実装を行います。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.preprocessing import StandardScaler# データの読み込み
data = pd.read_csv('Mall_Customers.csv')
# 必要な特徴量の選択
X = data[['Annual Income (k$)', 'Spending Score (1-100)']].values
# スケーリング(必要に応じて)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 階層型クラスタリングのための連結行列を計算
linked = linkage(X_scaled, method='ward') # ウォード法
# デンドログラムのプロット
plt.figure(figsize=(10, 7))
dendrogram(linked,
orientation='top',
distance_sort='descending',
show_leaf_counts=True)
plt.title('Dendrogram')
plt.xlabel('Data Points')
plt.ylabel('Euclidean Distance')
plt.show()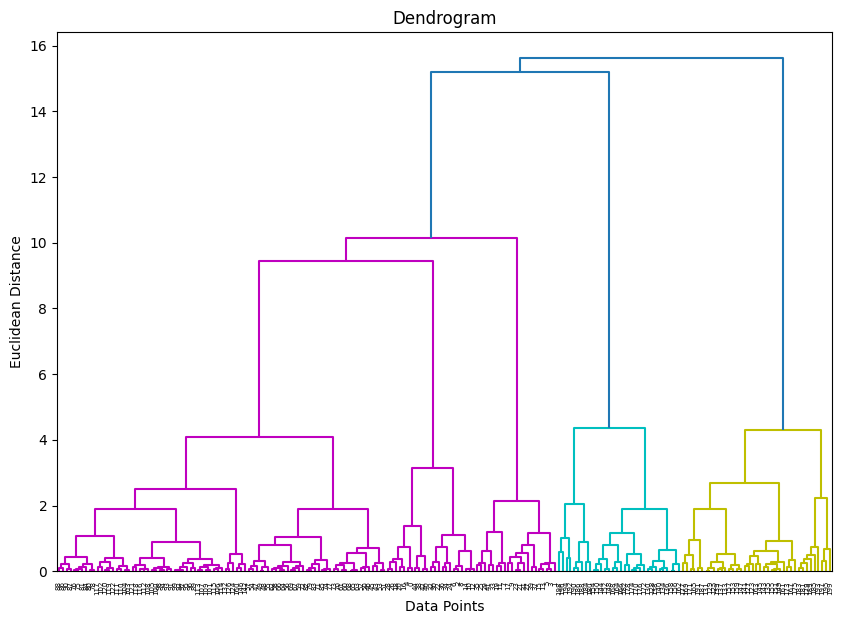
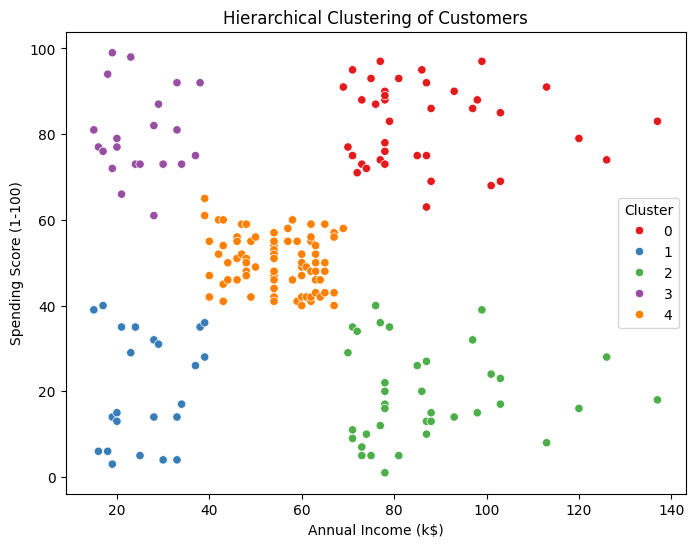
図では、約10〜12あたりの高さで大きく分岐しているのがわかります。この高さに水平線を引くと、
5つの大きなクラスタに分割されます。故にK=5となります。
特定の部分を表示させる方法:
# デンドログラムのプロット
plt.figure(figsize=(10, 7))
dendrogram(linked,
orientation='top',
distance_sort='descending',
show_leaf_counts=True,
truncate_mode='level', # 特定のレベルで切り捨て
p=3) # 最上位3つのレベルを表示
plt.title('Dendrogram (Truncated)')
plt.xlabel('Data Points')
plt.ylabel('Euclidean Distance')
plt.show()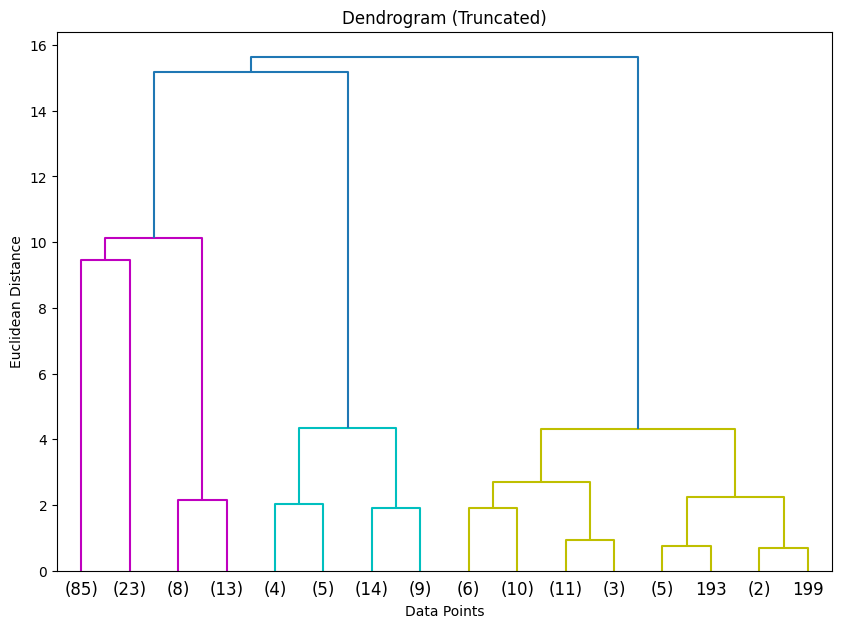
# 階層型クラスタリングのモデル定義
cluster = AgglomerativeClustering(n_clusters=5, linkage='ward') # 最適なK=5
# モデルの訓練と予測
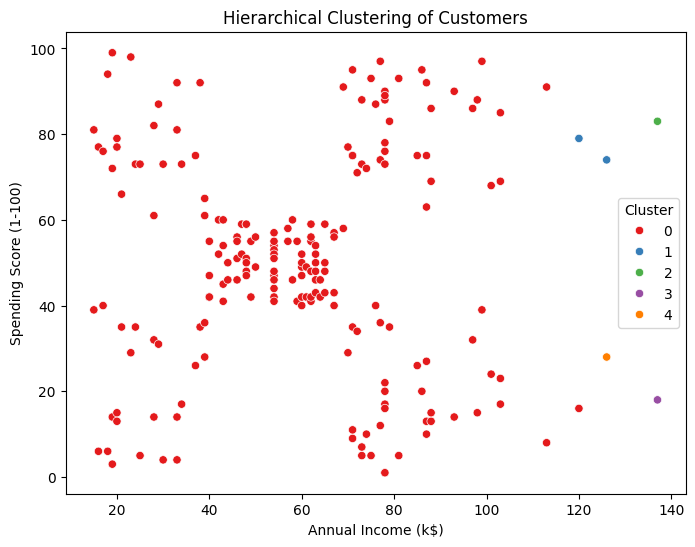
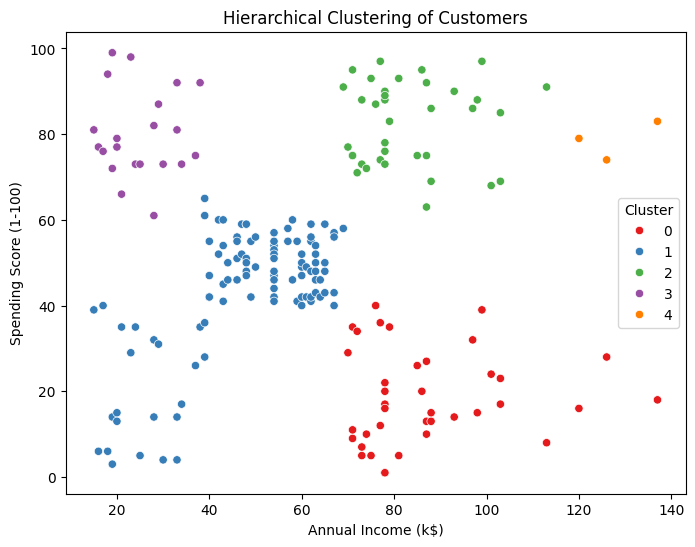
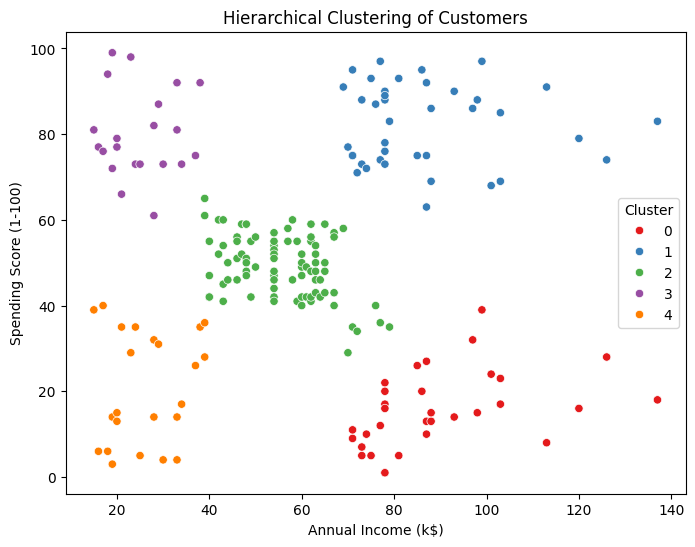
labels = cluster.fit_predict(X_scaled)# クラスタの可視化
plt.figure(figsize=(8, 6))
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=labels, palette='Set1')
plt.title('Hierarchical Clustering of Customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend(title='Cluster')
plt.show()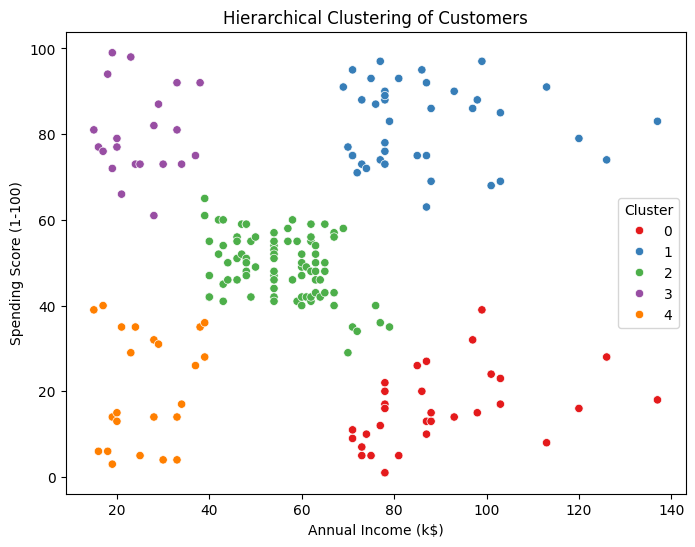
# 最短距離法(Single Linkage)
cluster_single = AgglomerativeClustering(n_clusters=5, linkage='single')
labels_single = cluster_single.fit_predict(X_scaled)
# 最長距離法(Complete Linkage)
cluster_complete = AgglomerativeClustering(n_clusters=5, linkage='complete')
labels_complete = cluster_complete.fit_predict(X_scaled)
# 可視化
fig, axes = plt.subplots(1, 2, figsize=(15, 6))
axes[0].scatter(X[:, 0], X[:, 1], c=labels_single, cmap='Set1')
axes[0].set_title('Single Linkage')
axes[0].set_xlabel('Annual Income (k$)')
axes[0].set_ylabel('Spending Score (1-100)')
axes[1].scatter(X[:, 0], X[:, 1], c=labels_complete, cmap='Set1')
axes[1].set_title('Complete Linkage')
axes[1].set_xlabel('Annual Income (k$)')
axes[1].set_ylabel('Spending Score (1-100)')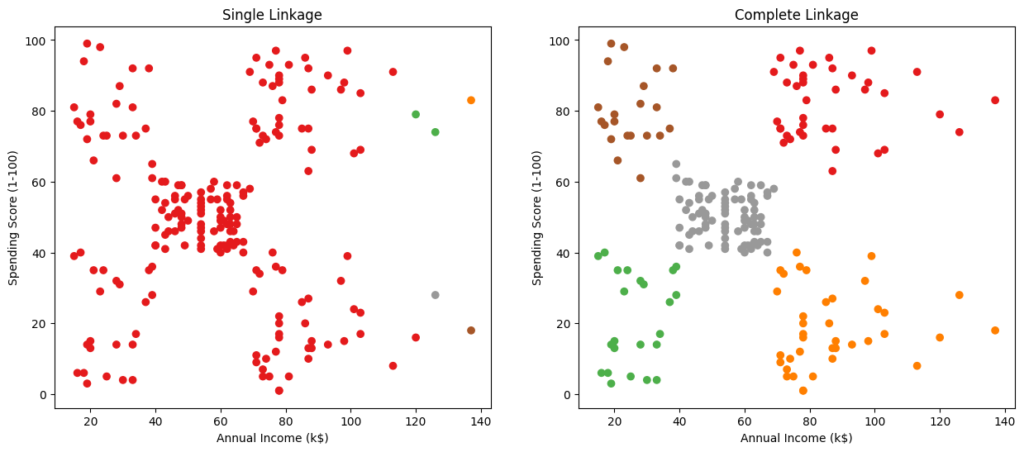
from sklearn.metrics import silhouette_score
# ウォード法によるクラスタリング
cluster_ward = AgglomerativeClustering(n_clusters=2, linkage='ward')
labels_ward = cluster_ward.fit_predict(X_scaled)
# シルエットスコアの計算
score = silhouette_score(X_scaled, labels_ward)
print(f'Silhouette Score (n_clusters=2): {score:.3f}')Silhouette Score (n_clusters=2): 0.554シルエットスコアは-1から1の値を取り、値が大きいほどクラスタリングの結果が良いことを示します。異なるクラスタ数でシルエットスコアを計算し、最適なクラスタ数を選択することができます。
# カラーパレットの設定
from scipy.cluster.hierarchy import set_link_color_palette
set_link_color_palette(['m', 'c', 'y', 'k'])
# デンドログラムのプロット(クラスタ数を指定)
plt.figure(figsize=(10, 7))
dendrogram(linked,
truncate_mode='lastp',
p=5,
show_leaf_counts=False,
leaf_rotation=90.,
leaf_font_size=12.,
show_contracted=True,
color_threshold=40)
plt.title('Truncated Dendrogram')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.show()Kaggleコンペティションへの応用
階層型クラスタリングは、Kaggleのデータ探索や前処理の段階で有用です。例えば、データの潜在的なグループを発見し、モデルの改善につなげることができます。
具体例:
- 顧客分析:顧客データをクラスタリングし、特徴的なセグメントを見つける。
- 画像解析:特徴量の類似性に基づいて画像をグループ化し、ラベルなしデータの構造を理解する。
- テキストマイニング:文書間の類似性を評価し、トピックの分類やキーワード抽出に役立てる。
階層クラスタリングの学習の整理
階層型クラスタリングは、データの階層的な関係を理解するための強力な手法です。デンドログラムを用いることで、データ間の結合過程を視覚的に把握でき、適切なクラスタ数の選択やデータの構造理解に役立ちます。
- 手法の選択:凝集型クラスタリングはデータの詳細な構造を捉えるのに適している。
- 距離計算方法:ウォード法はバランスの良いクラスタリング結果を得やすい。
- 可視化の重要性:デンドログラムや散布図を用いて結果を解釈する。
- 実装の工夫:大規模データでは計算効率を考慮し、必要に応じてデータをサンプリングする。
k-means法と階層クラスタリングの違い
| 比較項目 | K-means法 | 階層クラスタリング |
|---|---|---|
| 目的 | 両方とも、データを似た特性を持つグループ(クラスタ)に分け、データの構造を理解しやすくすることが目的。 | 両方とも、データを似た特性を持つグループ(クラスタ)に分け、データの構造を理解しやすくすることが目的。 |
| データの分割 | データポイントをクラスタに分けて、データのパターンや関係性を明らかにする。 | データポイントをクラスタに分けて、データのパターンや関係性を明らかにする。 |
| アルゴリズムのアプローチ | 指定したクラスタ数(K)に基づき、ランダムに選ばれた初期中心に近いデータを割り当て、中心を更新するプロセスを繰り返す。 | データポイントを階層的にグループ化し、凝集型または分割型アプローチでクラスタを形成。デンドログラムで視覚化される。 |
| クラスタ数の決定 | クラスタ数を事前に指定し、エルボー法などで適切なクラスタ数を選択する。 | クラスタ数を事前に指定する必要はなく、デンドログラムで視覚的にクラスタ数を決定できる。 |
| 計算の複雑さ | 比較的速く、大規模データにも効率的に動作する。 | 計算が複雑で、データが多い場合は計算時間が長くなることがある。 |
次回予告
次回は、教師なし学習のさらなる応用として、非線形次元削減手法や生成モデルについて学びます。これらの手法は、データの複雑な構造を理解し、新たなデータの生成や高度な特徴量抽出に役立ちます。ぜひお楽しみに。



コメント