【第2回】確率統計と最適化手法による機械学習の深化

このブログの目的

機械学習はさまざまな分野で活用されており、その基礎となる数学の理解が重要視されています。本シリーズでは、日本の高校生でも理解できる範囲で、機械学習を支える数学の基礎を3回にわたって解説します。

機械学習を理解するための基礎作り
このシリーズでは、機械学習を学ぶために必要な数学の基礎をわかりやすく紹介します。数式をただ覚えるのではなく、「なぜこの数学が必要なのか」を一緒に考えていきます。

難しい概念もゆっくりサポート
難しそうな数式や考え方が出てきても、安心してください。各トピックごとに、例を交えながら一歩ずつ進んでいきます。例えば、微分がどうして重要なのか、行列がどう使われるのかなど、学ぶ意味がわかるように説明します。

自分のペースで学べる工夫
急ぐ必要はありません。このシリーズは、わからないところがあっても気にせず、自分のペースで学べるようにサポートする内容になっています。例題を多く使い、実際に使える知識にしていきます。

前回の振り返り

前回は、機械学習の基礎となる線形代数と微分積分について学びました。これらの数学的概念が、どのようにして機械学習アルゴリズムの設計や解析に活用されるのかを理解することができたと思います。

今回のテーマは「確率統計と最適化手法による機械学習の深化」です。機械学習のモデルは、データの不確実性を扱う確率統計の知識と、モデルを最適化するための手法に大きく依存しています。本稿では、これらの数学的基礎について詳しく説明し、機械学習への応用例を紹介します。

第2回の目標

確率統計と最適化手法に焦点を当て、これらの数学的な概念がどのようにして機械学習の理解を深め、実際のデータ分析に役立つのかを探っていきます。これからの学習を通じて、データに対する見方をより広げ、実践的なスキルを身につけていくことができるでしょう。

確率と統計の基本を理解する：確率論やさまざまな確率分布について学び、データの不確実性をどのように表現するのかを把握します。
ベイズ推論を活用する：ベイズの定理の概念を理解し、ナイーブベイズ分類器やベイジアンネットワークなどの具体的な応用方法を探ります。
データの関係を数学的に分析する：共分散や相関の概念を使って、データ間の関係をどのように分析し、洞察を得るかを学びます。
最適化手法の基礎をマスターする：勾配降下法や確率的勾配降下法などの最適化手法を学び、これらが機械学習モデルのトレーニングにどのように役立つかを理解します。
統計的推論を実践する：推測統計や仮説検定の技術を習得し、データから得られる情報をどのように評価し、信頼性を確保するかを学びます。

このような目標を通じて、機械学習における数学的な基盤をしっかりと築いていくことができるでしょう。次のステップに進む準備を整え、知識を深めていくことに期待が高まります。

確率と統計

機械学習では、データの不確実性を理解し、適切にモデル化することが重要です。ここでは、確率論と統計学の基本概念について学びます。

確率論

確率論は、ランダムな現象の発生確率を数学的に扱う分野です。機械学習では、データの不確実性をモデル化するために確率論が用いられます。

データの不確実性のモデリング

例題：コインを10回投げて表が出る回数の確率を求める。

計算例：コイン投げはベルヌーイ試行であり、表が出る確率を $p=0.5$ とします。10回中 $k$ 回表が出る確率は二項分布で表されます。

$$P(X = k) = \binom{10}{k} p^k (1 – p)^{10 – k}$$

例えば、5回表が出る確率は

$$P(X = 5) = \binom{10}{5} (0.5)^5 (0.5)^5 = 252 \times \frac{1}{1024} \approx 0.246$$

計算の仕方

組み合わせの公式：組み合わせは選択の順序を無視し、特定のアイテムのグループを選ぶ際に使います。

$$C(n, r) = \frac{n!}{r!(n – r)!}$$

組み合わせは、n個のアイテムからr個を選ぶ方法の数を示します。この際、選ぶ順序は考慮されません。たとえば、5種類の果物から3つを選ぶ場合、りんご、バナナ、オレンジを選んだとき、バナナ、オレンジ、りんごを選んだ場合と同じとみなされます。

順列とその公式

順列の公式：順列は選択の順序を重視し、特定のアイテムの並びを考える場合に用います。

$$P(n, r) = \frac{n!}{(n – r)!}$$

順列は、n個のアイテムからr個を選び、選んだアイテムの順序を考慮して並べる方法の数を示します。たとえば、5種類の果物から3つを選ぶ場合、りんご、バナナ、オレンジの組み合わせと、バナナ、オレンジ、りんごの組み合わせは異なる順列としてカウントされます。

組み合わせの計算を以下に詳細に示します。特定の数値を用いて、組み合わせ$\binom{5}{10}$を計算します。

計算手順：

$$C(n, r) = \frac{n!}{r!(n – r)!}$$

この場合、$n=10$ および $r=5$です。

階乗の計算：

$$n!=10!=10×9×8×7×6×5×4×3×2×1=3628800$$

$$r!=5!=5×4×3×2×1=120$$

$$(n−r)!=(10−5)!=5!=120$$

組み合わせの計算：

$$\binom{10}{5} = \frac{10!}{5!(10-5)!} = \frac{3628800}{120 \times 120} = \frac{3628800}{14400} = 252$$

成功の確率：

$$(0.5)^5 = 0.5 \times 0.5 \times 0.5 \times 0.5 \times 0.5 = \frac{1}{32} \approx 0.03125$$

失敗の確率：

$$(0.5)^5 = 0.5 \times 0.5 \times 0.5 \times 0.5 \times 0.5 = \frac{1}{32} \approx 0.03125$$

全体の確率計算：

$$P(X = 5) = \binom{10}{5} \times (0.5)^5 \times (0.5)^5 = 252 \times \left(\frac{1}{32}\right) \times \left(\frac{1}{32}\right) = 252 \times \frac{1}{1024} \approx 0.246$$

確率論の実装

import math

# 二項確率関数の定義
def binomial_probability(n, k, p):  # 試行回数n、成功回数k、成功確率p
    comb = math.comb(n, k)  # n回の試行からk回成功する組み合わせの数を計算
    return comb * (p ** k) * ((1 - p) ** (n - k))

# 変数の設定
n = 10
p = 0.5
k = 5

# 確率の計算と出力
prob = binomial_probability(n, k, p)
print(f"P(X={k}) = {prob:.4f}")

P(X=5) = 0.2461

ベイズ推論

ベイズ推論は、観測データをもとに未知のパラメータの確率分布を更新する方法です。ベイズの定理を用いて、事後確率を計算します。

$$P(\theta|X) = \frac{P(X|\theta) P(\theta)}{P(X)}$$

$P(θ∣X)$ は事後確率
$P(X∣θ)$ は尤度
$P(θ)$ は事前確率
$P(X)$ は証拠

ベイズ推論の使い方

使用局面	説明
分類問題	ナイーブベイズ分類器を使用して、特徴量が独立であると仮定し、新しいデータポイントの所属クラスを予測します。
パラメータ推定	モデルのパラメータを事前分布とデータからの尤度を組み合わせて事後分布を求め、最も可能性の高いパラメータを特定します。
不確実性の扱い	データの不確実性や変動を考慮しながら予測を行うため、リスク評価や意思決定の場面で有用です。
異常検知	正常なデータの分布をモデル化し、新しいデータがその分布から外れているかどうかを評価して異常値を特定します。

例題

ある病気の事前確率が1%で、検査の正確性が99%（陽性の場合、病気である確率も99%）の場合、検査が陽性だったときの病気である確率を求める。

計算例：ベイズの定理を用いて計算

$$P(\text{病気}|\text{陽性}) = \frac{P(\text{陽性}|\text{病気})P(\text{病気})}{P(\text{陽性})}$$

$$P(\text{陽性}) = P(\text{陽性}|\text{病気})P(\text{病気}) + P(\text{陽性}|\text{健康})P(\text{健康})$$

数値を代入すると：

$$P(\text{陽性}) = 0.99 \times 0.01 + 0.01 \times 0.99 = 0.0198$$

$$P(\text{病気}|\text{陽性}) = \frac{0.99 \times 0.01}{0.0198} \approx 0.5$$

ベイズ推論の実装

def bayes_theorem(P_A, P_B_given_A, P_B_given_not_A):
    P_not_A = 1 - P_A
    P_B = P_B_given_A * P_A + P_B_given_not_A * P_not_A
    return (P_B_given_A * P_A) / P_B  # ベイズの定理

P_disease = 0.01
P_positive_given_disease = 0.99
P_positive_given_health = 0.01

posterior = bayes_theorem(P_disease, P_positive_given_disease, P_positive_given_health)
print(f"検査が陽性だったときの病気である確率: {posterior:.2f}")

# P_A: 事象A（病気である確率）の事前確率。
# P_B_given_A: 事象Aが真であるときの事象B（検査が陽性である確率）= 事後確率
# P_B_given_not_A: 事象Aが偽であるときの事象Bの確率 = 尤度
# P_B：陽性の確率 = 全確率

検査が陽性だったときの病気である確率: 0.50

確率分布

確率分布は、ランダム変数が取りうる値とその確率を記述します。代表的な分布には以下のものがあります。

正規分布

正規分布は、自然現象や測定誤差の分布をモデル化するために広く用いられ、中心極限定理により多くの統計的手法や推測において基盤となります。

正規分布の確率密度関数（PDF）

$$f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{(x – \mu)^2}{2\sigma^2}\right)$$

平均 $μ$ と分散 $σ^2 $を持ち、自然現象や測定誤差によく適用されます。

例題

平均 $μ=0$ 分散 $σ_2=1$ の正規分布における $x=1$ の確率密度を求める。

計算例

$$f(1) = \frac{1}{\sqrt{2\pi \times 1}} \exp \left( -\frac{(1-0)^2}{2 \times 1} \right) \approx 0.24197$$

正規分布の実装

import math
import numpy as np
import matplotlib.pyplot as plt  

# 正規分布の確率密度関数の定義
def normal_distribution(x, mu, sigma_sq):
    return (1 / math.sqrt(2 * math.pi * sigma_sq)) * math.exp(-((x - mu) ** 2) / (2 * sigma_sq))

mu = 0
sigma_sq = 1
x = 1
density = normal_distribution(x, mu, sigma_sq)
print(f"正規分布 N(0,1) における x=1 の確率密度: {density:.5f}")

# 可視化のためのコードを追加
x_values = np.linspace(-4, 4, 100)  # xの範囲を設定
y_values = [normal_distribution(x_val, mu, sigma_sq) for x_val in x_values]  # 確率密度を計算

plt.plot(x_values, y_values)  # グラフを描画
plt.title('正規分布 N(0,1)')  # タイトル
plt.xlabel('x')  # x軸ラベル
plt.ylabel('確率密度')  # y軸ラベル
plt.grid()  # グリッドを表示
plt.show()  # グラフを表示

正規分布 N(0,1) における x=1 の確率密度: 0.24197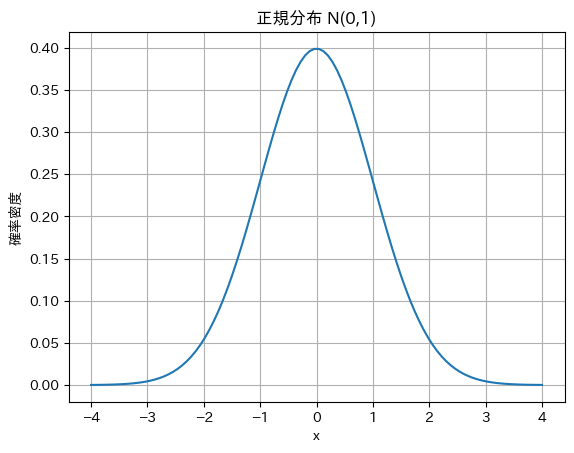

$f(x)$ は確率密度関数であるため、特定の範囲内の曲線下の面積は、その範囲内の値を観測する確率として解釈できます。

ベルヌーイ分布

ベルヌーイ分布は、成功確率 $( p )$ を持つ二項試行における結果を表し、成功（1）または失敗（0）のいずれかの結果が得られる確率分布です。

$$P(X=1)=p,P(X=0)=1−p$$

成功確率 $p$ の二項分布で、二値分類問題に適用されます。

例題

成功確率 $p=0.3$ のベルヌーイ試行において、成功（1）が起こる確率を求める。

計算例

$$P(X = 1) = 0.3, \quad P(X = 0) = 0.7$$

ベルヌーイの実装

def bernoulli_pmf(k, p):
    if k == 1:
        return p
    elif k == 0:
        return 1 - p
    else:
        return 0

p = 0.3
k = 1
prob_success = bernoulli_pmf(k, p)
print(f"P(X={k}) = {prob_success:.2f}")

P(X=1) = 0.30

ポアソン分布

ポアソン分布は確率質量関数（PMF）を用いて定義されます。ポアソン分布の確率質量関数は、特定のイベントが一定の時間または空間内に何回発生するかの確率を計算するための数式です。

ポアソン分布は、単位時間または単位空間内に発生する稀なイベントの発生回数をモデル化する確率分布で、平均発生率 $λ$ に基づいて定義されます。

$$P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}$$

$λ$ は平均発生率、$k$ は発生回数、$e$ は自然対数の底です。

例題

平均発生率 $λ=4$ のポアソン分布において、ちょうど $k=3$ 回のイベントが発生する確率を求める。

計算例

$$P(X = 3) = \frac{4^3 e^{-4}}{3!} = \frac{64 \times e^{-4}}{6} \approx 0.1954$$

計算手順

$λ^k$ の計算

$$λ^3=4^3=64$$

$e^{−λ}$ の計算

$$e^{−4}≈0.0183156 (計算機を使用して評価)$$

$k!$ の計算

$$3!=3×2×1=6$$

確率の計算

$$P(X = 3) = \frac{64 \times e^{-4}}{6} = \frac{64 \times 0.0183156}{6} \approx \frac{1.1721584}{6} \approx 0.1953668$$

したがって、ポアソン分布において、ちょうど3回のイベントが発生する確率 $P(X=3)$は約 0.1954 です。この確率は、平均発生率が4の状況下での特定のイベントの発生をモデル化したものです。

ポアソン分布の実装

import math
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

# ポアソン分布の確率質量関数（PMF）を計算する関数を定義
def poisson_pmf(k, lambd):
    return (lambd ** k * math.exp(-lambd)) / math.factorial(k)

lambd = 4  # 平均発生率
k = 3  # 成功の回数
k_values = np.arange(0, 15)  # kの範囲を設定（0から14まで）

prob = poisson_pmf(k, lambd)
print(f"P(X={k}) = {prob:.4f}")

# 各kに対するポアソンPMFを計算
probabilities = [poisson_pmf(k, lambd) for k in k_values]

# 可視化
plt.bar(k_values, probabilities, color='blue', alpha=0.7)
plt.title('ポアソン分布 PMF (λ=4)')
plt.xlabel('成功の回数 (k)')
plt.ylabel('確率 P(X=k)')
plt.xticks(k_values)  # x軸の目盛りを設定
plt.grid(axis='y')  # y軸のグリッドを表示
plt.show()  # グラフを表示

P(X=3) = 0.1954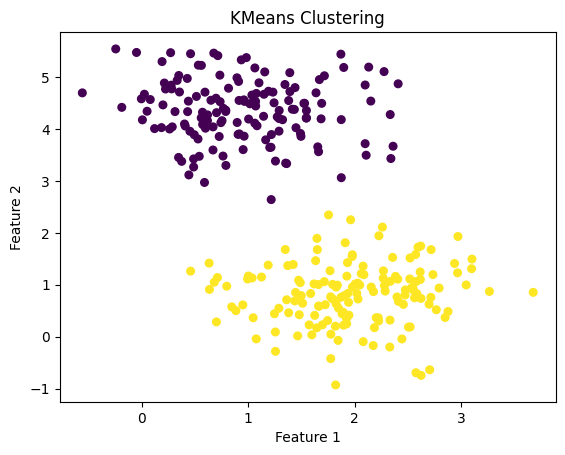

ベイズの定理

ナイーブベイズ分類器

特徴量が互いに独立であると仮定し、事後確率を計算してクラスを予測します。

ベイズの定理

ベイズの定理は、事前情報と新しい証拠を統合して事後確率を更新する方法です。ベイズ的アプローチは、以下のように機械学習モデルに応用されます。

ベイズの定理は、先ほどの病気の例で説明しました。ここでは、ナイーブベイズ分類器の具体例を示します。

例題

スパムメール分類において、あるメールがスパムである確率を求める。

計算例

スパムメールの事前確率 $P$(スパム)=0.4
単語 “無料” がスパムメールに含まれる確率 $P$(“無料”∣スパム)=0.6
単語 “無料” が非スパムメールに含まれる確率$P$(“無料”∣非スパム)=0.1

メールに “無料” が含まれている場合のスパムである確率$P$(スパム∣”無料”)を求めます。

$P(\text{スパム} | \text{無料}) = \frac{P(\text{無料} | \text{スパム}) P(\text{スパム})}{P(\text{無料})}$

$P(\text{無料}) = P(\text{無料} | \text{スパム}) P(\text{スパム}) + P(\text{無料} | \text{非スパム})P(\text{非スパム}) =$
$0.6 \times 0.4 + 0.1 \times 0.6 = 0.24 + 0.06 = 0.3$

$P(\text{スパム} | \text{無料}) = \frac{0.6 \times 0.4}{0.3} = 0.8$

ナイーブベイズ分類器の実装

def naive_bayes(spam_prior, word_given_spam, word_given_not_spam):
    P_spam = spam_prior
    P_not_spam = 1 - P_spam
    P_word = word_given_spam * P_spam + word_given_not_spam * P_not_spam
    P_spam_given_word = (word_given_spam * P_spam) / P_word
    return P_spam_given_word

spam_prior = 0.4
P_word_given_spam = 0.6
P_word_given_not_spam = 0.1

posterior = naive_bayes(spam_prior, P_word_given_spam, P_word_given_not_spam)
print(f"メールに '無料' が含まれている場合のスパムである確率: {posterior:.2f}")

メールに '無料' が含まれている場合のスパムである確率: 0.80

ナイーブベイズ分類器の応用

ナイーブベイズ分類器を用いて簡単なデータセットを分類する。

from sklearn.naive_bayes import GaussianNB
import numpy as np

# サンプルデータ: [特徴1, 特徴2]
X = np.array([[1.0, 2.1],
              [1.5, 1.8],
              [5.0, 8.0],
              [6.0, 9.0],
              [1.2, 0.9],
              [5.5, 8.5]])

# ラベル: 0 = 非スパム, 1 = スパム
y = np.array([0, 0, 1, 1, 0, 1])

# ナイーブベイズ分類器の訓練
model = GaussianNB()
model.fit(X, y)

# 新しいデータの予測
new_data = np.array([[1.1, 1.0],
                     [5.2, 9.0]])
predictions = model.predict(new_data)
print(f"新しいデータの予測ラベル: {predictions}")

新しいデータの予測ラベル: [0 1]

ベイジアンネットワーク

複数の確率変数間の依存関係をグラフ構造で表現し、複雑な依存関係をモデル化します。

ベイジアンネットワークは、確率変数間の因果関係を有向非循環グラフで表現するモデルです。このネットワークは、条件付き独立性の概念を利用して、複雑な確率分布を簡潔に記述します。各ノードは確率変数を表し、エッジはその変数間の依存関係を示します。ベイジアンネットワークを使用すると、観測データに基づいて確率を更新し、推論を行うことができます。

$$P(X_1, X_2, \ldots, X_n) = \prod_{i=1}^{n} P(X_i \mid \text{Pa}(X_i))$$

$P(X_i∣Pa(X_i))$ はノード $X_i$ の親ノードに基づく条件付き確率です。
$n$ はネットワーク内の変数の数です。

例題

雨が降っている場合、交通渋滞の確率がどのように変化し、その影響で事故が発生する確率はどのようになるか？

モデルの定義

$R$：雨が降る（1）または降らない（0）
$T$：交通渋滞が発生する（1）または発生しない（0）
$A$：事故が発生する（1）または発生しない（0）

条件付き確率の設定

$P(R=1)=0.3$：雨が降る確率は30%
$P(T=1∣R=1)=0.8$：雨が降るときの交通渋滞発生確率は80%
$P(T=1∣R=0)=0.4$：雨が降らないときの交通渋滞発生確率は40%
$P(A=1∣T=1)=0.9$：交通渋滞があるときの事故発生確率は90%
$P(A=1∣T=0)=0.1$：交通渋滞がないときの事故発生確率は10%

計算式

雨が降っている場合の事故が発生する確率を計算します。

交通渋滞が発生する確率：

$$P(T=1∣R=1)=0.8$$

事故が発生する確率：

$$P(A=1∣T=1)=0.9$$

雨が降る場合の事故発生確率：

$$(A=1∣R=1)=P(A=1∣T=1)⋅P(T=1∣R=1)=0.9⋅0.8=0.72$$

ベイジアンネットワーク実装

# 必要なライブラリのインポート
from pgmpy.models import BayesianModel
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
import matplotlib.pyplot as plt

# ベイジアンネットワークのモデルを定義
model = BayesianModel([('Rain', 'Traffic'), ('Traffic', 'Accident')])

# 条件付き確率分布（CPD）の定義
cpd_rain = TabularCPD(variable='Rain', variable_card=2, values=[[0.7], [0.3]])  # P(Rain)
cpd_traffic = TabularCPD(variable='Traffic', variable_card=2,
                         values=[[0.6, 0.2], [0.4, 0.8]],  # P(Traffic | Rain)
                         evidence=['Rain'], evidence_card=[2])
cpd_accident = TabularCPD(variable='Accident', variable_card=2,
                          values=[[0.1, 0.9], [0.9, 0.1]],  # P(Accident | Traffic)
                          evidence=['Traffic'], evidence_card=[2])

# モデルにCPDを追加
model.add_cpds(cpd_rain, cpd_traffic, cpd_accident)

# モデルが正しく定義されているか確認
assert model.check_model()

# 変数間の推論を行う
inference = VariableElimination(model)
result = inference.query(variables=['Accident'], evidence={'Rain': 1})  # 雨が降っている場合の事故の確率

# 結果の表示
accident_prob = result.values[1]  # 事故が発生する確率
print(f"雨が降っている場合の事故の確率: {accident_prob:.2f}")

# 可視化のためのコードを追加
labels = ['事故が発生しない', '事故が発生する']
probabilities = [result.values[0], accident_prob]  # 事故が発生しない確率と発生する確率

plt.bar(labels, probabilities, color=['green', 'red'], alpha=0.7)
plt.title('雨が降っている場合の事故の確率')
plt.ylabel('確率')
plt.ylim(0, 1)  # y軸の範囲を設定
plt.show()  # グラフを表示

雨が降っている場合の事故の確率: 0.26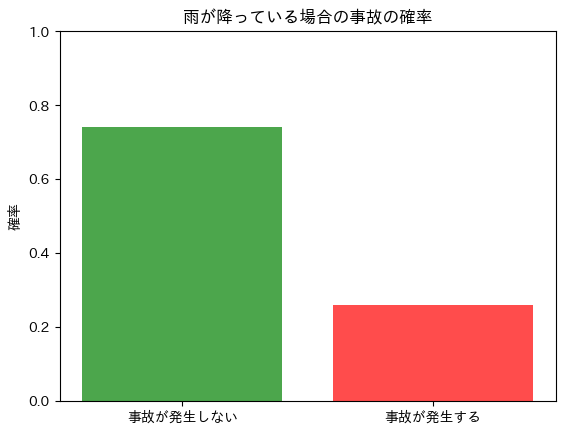

期待値と分散

期待値は確率変数の平均、分散はデータのばらつきを表します。

これらの指標は、特徴量の中心傾向と分散を理解するために使用されます。

$$E[X] = \mu = \sum_{i} x_i P(x_i)$$

$$Var(X) = \sigma^2 = E[X^2] – (E[X])^2$$

特徴量の平均とばらつきの理解

例題

データセット [2,4,6,8,10] の期待値（平均）と分散を計算する。

計算例

$$E[X] = \mu = \frac{2 + 4 + 6 + 8 + 10}{5} = 6$$

$$Var(X) = \sigma^2 = \frac{(2 – 6)^2 + (4 – 6)^2 + (6 – 6)^2 + (8 – 6)^2 + (10 – 6)^2}{5} = \frac{16 + 4 + 0 + 4 + 16}{5} = 8$$

import numpy as np

data = np.array([2, 4, 6, 8, 10])
mean = np.mean(data)
variance = np.var(data)
print(f"平均 (期待値): {mean}")
print(f"分散: {variance}")

平均 (期待値): 6.0
分散: 8.0

共分散と相関

共分散は二つの変数の同時変動を測定し、相関はその関係の強さと方向を示します。

$$\text{Cov}(X, Y) = E[(X – E[X])(Y – E[Y])]$$

$$\rho_{X,Y} = \frac{\text{Cov}(X,Y)}{\sigma_X \sigma_Y}$$

データ間の相関関係の分析方法

例題

データセット [1,2,3,4,5] と [2,4,6,8,10] の共分散と相関係数を計算する。

計算例

$$\text{Cov}(X, Y) = E[(X – \mu_X)(Y – \mu_Y)] = \frac{(1 – 3)(2 – 6) + (2 – 3)(4 – 6) + \cdots + (5 – 3)(10 – 6)}{5} = 8$$

$$\rho_{X,Y} = \frac{\text{Cov}(X,Y)}{\sigma_X \sigma_Y} = \frac{8}{\sqrt{2} \times \sqrt{8}} = 1$$

$\text{Cov}(X, Y)$= 共分散
$\rho_{X,Y}$ = 相関係数

共分散と相関

import numpy as np

X = np.array([1, 2, 3, 4, 5])
Y = np.array([2, 4, 6, 8, 10])

cov_matrix = np.cov(X, Y, bias=True)
cov_xy = cov_matrix[0, 1]
correlation = np.corrcoef(X, Y)[0, 1]

print(f"共分散: {cov_xy}")
print(f"相関係数: {correlation}")

共分散: 4.0
相関係数: 0.9999999999999999

推測統計

推測統計は、サンプルデータから母集団の特性を推定する方法です。代表的な手法には点推定や区間推定があります。

サンプルから母集団を推測する方法

例題

サンプルデータ [5,7,8,9,10] から母集団の平均を推定する。

計算例：サンプル平均を用いて母集団の平均を推定します。

$$\hat{\mu} = \frac{5 + 7 + 8 + 9 + 10}{5} = 7.8$$

import numpy as np

sample = np.array([5, 7, 8, 9, 10])
sample_mean = np.mean(sample)
print(f"推定された母集団の平均: {sample_mean}")

推定された母集団の平均: 7.8

平均の区間推定の例

例題：サンプルデータ [5,7,8,9,10] の95%信頼区間を求める。

計算例：サンプル平均 $\hat{\mu} = 7.8$、サンプル標準偏差 $s=1.923$、サンプルサイズ $n=5$ です。t分布を用いて信頼区間を計算します。

$$\text{信頼区間} = \hat{\mu} \pm t_{\alpha/2, n-1} \times \frac{s}{\sqrt{n}}$$

自由度 $df=4$、95%信頼区間のt値 $t_{0.025,4}≈2.776$

$$7.8 \pm 2.776 \times \frac{1.923}{\sqrt{5}} \approx 7.8 \pm 2.396$$
$$\text{信頼区間} \approx [5.404, 10.196]$$

平均区間推定の実装

import numpy as np
from scipy import stats

sample = np.array([5, 7, 8, 9, 10])
confidence = 0.95
n = len(sample)
mean = np.mean(sample)
std_err = stats.sem(sample)
t_critical = stats.t.ppf((1 + confidence) / 2, df=n-1)
margin_of_error = t_critical * std_err
confidence_interval = (mean - margin_of_error, mean + margin_of_error)

print(f"95% 信頼区間: {confidence_interval}")

95% 信頼区間: (5.411611611900016, 10.188388388099984)

仮説検定

仮説検定は、統計的仮説の妥当性を評価する方法です。機械学習では、モデルのパフォーマンス評価やデータの有意性検定に用いられます。

モデルのパフォーマンス評価

例題：二つのモデルの精度が統計的に有意に異なるかを検定する。

計算例：モデルAの精度が80%、モデルBの精度が85%で、サンプルサイズが100の場合、二項検定を行います。

仮説の設定

帰無仮説 $H_0$：モデルAとモデルBの精度に差はない（$p_A=p_B$）。
対立仮説 $H_1$：モデルAとモデルBの精度に差がある（$p_A≠p_B$）。

精度とサンプルサイズの定義

モデルAの精度： $p_A=0.80$
モデルBの精度： $p_B=0.85$
サンプルサイズ： $n=100$

二項検定の計算

モデルAの成功数（正しく予測した数）とモデルBの成功数を計算します。

モデルAの成功数

$$k_A = n_A \cdot p_A = 100 \cdot 0.80 = 80$$

モデルBの成功数

$$k_B = n_B \cdot p_B = 100 \cdot 0.85 = 85$$

プールされた成功率の計算

プールされた成功率 $p$ を計算します。これは、二つのモデルの成功数を合計し、全サンプルサイズで割った値です。

$$p = \frac{k_A + k_B}{n_A + n_B} = \frac{80 + 85}{100 + 100} = \frac{165}{200} = 0.825$$

標準誤差の計算

成功率の標準誤差 $SE$ は次のように計算されます

$$SE = \sqrt{p(1 – p) \left( \frac{1}{n_A} + \frac{1}{n_B} \right)} = \sqrt{0.825 \times (1 – 0.825) \left( \frac{1}{100} + \frac{1}{100} \right)} = 0.0537$$

Zスコアの計算

次に、Zスコアを計算します。Zスコアは、モデルAとモデルBの成功率の差を標準誤差で割ったものです。

$$Z = \frac{(p_A – p_B)}{SE} = \frac{(0.80 – 0.85)}{0.0537} = 0.93$$

仮説検定を実装

from scipy import stats

# モデルAとモデルBの正解数
success_a = 80
n_a = 100
success_b = 85
n_b = 100

# 精度の差を検定
prop_a = success_a / n_a
prop_b = success_b / n_b
pooled_prop = (success_a + success_b) / (n_a + n_b)
std_error = math.sqrt(pooled_prop * (1 - pooled_prop) * (1/n_a + 1/n_b))
z = (prop_b - prop_a) / std_error
p_value = 2 * (1 - stats.norm.cdf(abs(z)))

print(f"Z値: {z:.2f}")
print(f"P値: {p_value:.4f}")

Z値: 0.93
P値: 0.3521

解釈：P値が0.3521であり、通常の有意水準（例えば0.05）より大きいため、モデルAとモデルBの精度の差は統計的に有意ではないと結論付けられます。帰無仮説は棄却できない。

データの有意性検定の手法（片側t検定の説明）

例題：学生の試験点数が平均70点より有意に高いかを検定する。

計算例：サンプルデータ [72,75,78,80,85] の平均が70点より高いかを片側t検定で検証します。

片側t検定は、特定の仮説（例えば、平均がある値よりも高いまたは低いか）を検証するための統計的手法です。この場合、学生の試験点数が平均70点より有意に高いかどうかを検証します。

仮説の設定

帰無仮説 $H_0$：学生の平均点は70点である（$μ=70$）。
対立仮説 $H_1$：学生の平均点は70点より高い（$μ>70$）。

t検定の数式

片側t検定のt値は、次の数式で計算されます。

$$t = \frac{\bar{x} – \mu_0}{s / \sqrt{n}}$$

$\bar{x}$ はサンプルの平均
$μ_0$ は帰無仮説での平均（この場合は70点）
$s$ はサンプルの標準偏差
$n$ はサンプルサイズ

片側t検定の実装

import numpy as np
from scipy import stats

sample = np.array([72, 75, 78, 80, 85])
mu = 70
n = len(sample)
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1)
std_err = sample_std / math.sqrt(n)
t_stat = (sample_mean - mu) / std_err
p_value = 1 - stats.t.cdf(t_stat, df=n-1)

print(f"t統計量: {t_stat:.2f}")
print(f"P値: {p_value:.4f}")

t統計量: 3.61
P値: 0.0112

解釈： P値が0.0112であり、通常の有意水準（0.05）より小さいため、学生の試験点数は平均70点より有意に高いと結論付けられます。帰無仮説は棄却できる。

期待値と分散、共分散、相関、推測統計、仮説検定、t検定などは詳しくは以下を参照して下さい。

最適化

機械学習モデルの訓練は、損失関数を最小化する最適化問題として定式化されます。ここでは、代表的な最適化手法について具体的な計算例とPythonコードを用いて説明します。

詳しくは以下を参照。

勾配降下法

例題：損失関数 $J(θ)=θ^2$ の最小値を勾配降下法で求める。

計算例：初期値 θ_0=10 、学習率 $η=0.1$ とします。

更新式

$$\theta_{n+1} = \theta_n – \eta \nabla_\theta J(\theta_n) = \theta_n – \eta \times 2 \theta_n = \theta_n (1 – 2 \eta)$$

例えば、1ステップ目

$$θ_1=10−0.1×2×10=10−2=8$$

import numpy as np
import matplotlib.pyplot as plt

# 損失関数の定義
def J(theta):
    return theta**2

# 勾配の定義
def gradient(theta):
    return 2 * theta

# 勾配降下法の実行
theta = 10.0  # 初期値
eta = 0.1     # 学習率
theta_values = [theta]
for _ in range(20):
    theta = theta - eta * gradient(theta)
    theta_values.append(theta)

# 損失関数のグラフ
theta_range = np.linspace(-12, 12, 400)
plt.plot(theta_range, J(theta_range), label='J(theta)')
plt.scatter(theta_values, [J(t) for t in theta_values], color='red')
plt.title('Gradient Descent on J(theta) = theta^2')
plt.xlabel('theta')
plt.ylabel('J(theta)')
plt.legend()
plt.grid(True)
plt.show()

確率的勾配降下法 (SGD)

SGDでは、全データセットではなく、ランダムに選ばれた1つのデータポイント（または小さなバッチ）に基づいてパラメータを更新します。これにより、計算が大幅に軽減され、収束が早くなることがあります。

$$\theta_{n+1} = \theta_n – \eta \nabla_\theta J_i(\theta_n)$$

$J_i(θ)$a は、選択したデータポイント $i$ に対する損失関数（例: 二乗誤差や交差エントロピー）です。
$∇J_i(θ)$ は、この損失関数の勾配を示します。

SGDの流れ

データポイントの選択：訓練データからランダムに1つのデータポイント $x_i$ を選びます。
勾配の計算：損失関数 $J_i$ を計算し、その勾配 $∇J_i(θ)$ を求めます。
パラメータの更新：上記のSGDの数式を用いて、パラメータ $θ$ を更新します。

特徴と利点

計算効率：SGDは各ステップで1つのデータポイントのみを使用するため、計算量が少なく、特に大規模データセットにおいて迅速に学習を行えます。
収束の速度：更新が頻繁に行われるため、パラメータが迅速に適応し、ローカルミニマムから脱出しやすい特徴があります。

大規模データへの適用と効率化

例題：大規模なデータセットに対して確率的勾配降下法を適用する。

簡単な線形回帰問題を例に、SGDを用いてパラメータを最適化します。

import numpy as np
import matplotlib.pyplot as plt

# サンプルデータの生成
np.random.seed(0)
X = 2 * np.random.rand(1000, 1)
y = 4 + 3 * X[:, 0] + np.random.randn(1000)

# ハイパーパラメータ
learning_rate = 0.01
n_iterations = 50
m = 1000

# パラメータの初期化
theta_0 = 0.0  # スカラーとして初期化
theta_1 = 0.0  # スカラーとして初期化

theta_0_history = []
theta_1_history = []
loss_history = []

for epoch in range(n_iterations):
    for i in range(m):
        random_index = np.random.randint(m)
        xi = X[random_index]
        yi = y[random_index]
        prediction = theta_0 + theta_1 * xi
        error = prediction - yi
        theta_0 -= learning_rate * error
        theta_1 -= learning_rate * error * xi[0]  # xiをスカラーとして扱う
    # 訓練後の損失を記録
    loss = np.mean((theta_0 + theta_1 * X[:, 0] - y) ** 2)
    theta_0_history.append(theta_0)
    theta_1_history.append(theta_1)
    loss_history.append(loss)
    print(f"Epoch {epoch+1}: Loss = {loss:.4f}")

# 結果のプロット
plt.plot(range(1, n_iterations+1), loss_history, marker='o')
plt.title('SGDによる損失の推移')
plt.xlabel('エポック')
plt.ylabel('損失')
plt.grid(True)
plt.show()

# bestθの表示
best_theta = (theta_0, theta_1)
print(f"bestθ: {best_theta}")

# bestθの可視化
plt.scatter(X, y, color='blue', label='データポイント')  # データポイントのプロット
X_fit = np.array([[0], [2]])  # 回帰直線のx範囲
y_fit = best_theta[0] + best_theta[1] * X_fit  # 回帰直線のy値
plt.plot(X_fit, y_fit, color='red', label='回帰直線')  # 回帰直線のプロット
plt.title('最適な回帰直線')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

Epoch 1: Loss = 0.9408
Epoch 2: Loss = 0.9544
Epoch 3: Loss = 0.9376
Epoch 4: Loss = 0.9442
Epoch 5: Loss = 0.9780
Epoch 6: Loss = 0.9452
Epoch 7: Loss = 0.9336
Epoch 8: Loss = 0.9355
Epoch 9: Loss = 0.9376
Epoch 10: Loss = 0.9583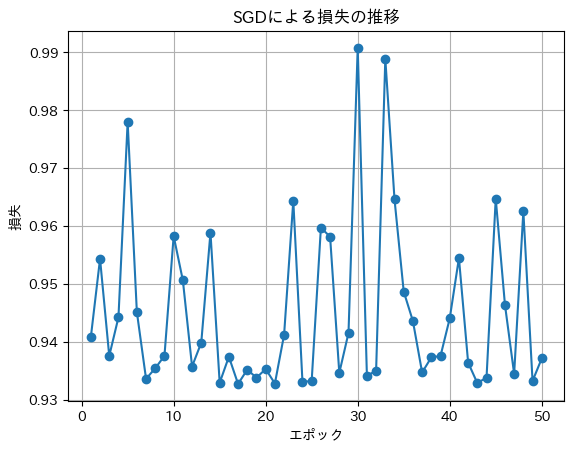

bestθ: (array([4.06731559]), array([3.01681403]))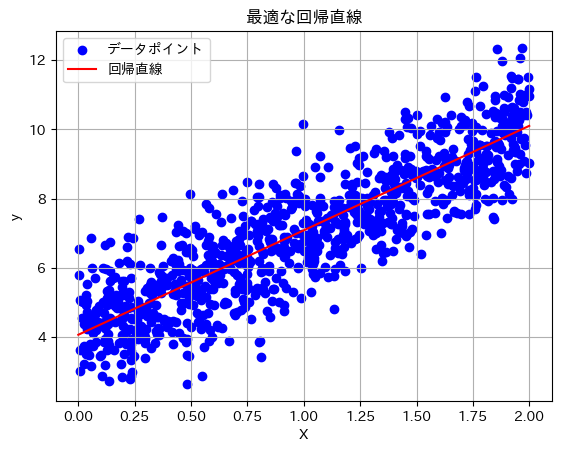

ラグランジュ最適化

ラグランジュ乗数法は、制約条件付きの最適化問題を解く方法です。例えば、サポートベクターマシン（SVM）では、マージンを最大化するためにラグランジュ最適化が用いられます。

制約条件付きの最適化問題の解法

例題：制約条件 $x+y=10$ の下で関数 $f(x, y) = x^2 + y^2$ を最小化する。

計算例：ラグランジュ関数を設定します。

$$\mathcal{L}(x, y, \lambda) = x^2 + y^2 + \lambda(10 – x – y)$$

各変数について偏微分し、ゼロとおきます。

$$\begin{align}
\frac{\partial L}{\partial x} &= 2x – \lambda = 0 \quad (1) \\
\frac{\partial L}{\partial y} &= 2y – \lambda = 0 \quad (2) \\
\frac{\partial L}{\partial \lambda} &= 10 – x – y = 0 \quad (3)
\end{align}$$

(1) と (2) より、$x=y$。(3) より、 $2x=10$ より $x=5$、$y=5$。

from sympy import symbols, Eq, solve

# シンボルの定義
x, y, lam = symbols('x y lambda')

# ラグランジュ関数の定義
L = x**2 + y**2 + lam * (10 - x - y)

# 偏微分
eq1 = Eq(L.diff(x), 0)
eq2 = Eq(L.diff(y), 0)
eq3 = Eq(L.diff(lam), 0)

# 方程式の解
solution = solve((eq1, eq2, eq3), (x, y, lam))
print(f"最適解: x = {solution[x]}, y = {solution[y]}, lambda = {solution[lam]}")

最適解: x = 5, y = 5, lambda = 10

サポートベクターマシン（SVM）

詳しくは以下を参照。

例題：制約条件付きでSVMのマージンを最大化する。

計算例：SVMでは、データポイントが線形に分離可能である場合、以下の最適化問題を解きます。

$$\begin{align}
\min_{w,b} \quad & \frac{1}{2} \| w \|^2 \\
\text{subject to} \quad & y_i (w \cdot x_i + b) \geq 1 \quad \forall i
\end{align}$$

from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt

# サンプルデータの生成
X = np.array([[2, 3],
              [3, 3],
              [3, 4],
              [5, 5],
              [1, 1],
              [2, 1],
              [1, 2],
              [2, 2]])
y = np.array([1, 1, 1, 1, -1, -1, -1, -1])

# SVMモデルの訓練
model = svm.SVC(kernel='linear')
model.fit(X, y)

# サポートベクターの取得
sv = model.support_vectors_

# 決定境界の取得
w = model.coef_[0]
b = model.intercept_[0]
x_plot = np.linspace(0, 6, 100)
y_plot = -(w[0] * x_plot + b) / w[1]

# プロット
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='bwr')
plt.scatter(sv[:, 0], sv[:, 1], s=100, facecolors='none', edgecolors='k', label='Support Vectors')
plt.plot(x_plot, y_plot, 'k-', label='Decision Boundary')
plt.title('SVMによる分類')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(True)
plt.show()

print(f"決定境界の式: {w[0]:.2f}x + {w[1]:.2f}y + {b:.2f} = 0")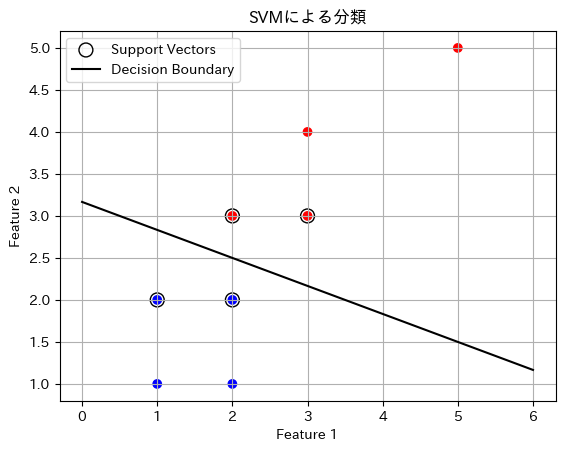

決定境界の式: 0.40x + 1.20y + -3.80 = 0

モーメント法

勾配降下法の安定化手法

例題：勾配降下法において、一階モーメント（移動平均）を用いて学習率を調整する。

計算例：Adamオプティマイザーの簡易版を実装します。

Adamは、勾配降下法を拡張したアルゴリズムで、学習率を各パラメータごとに調整します。過去の勾配を考慮し、勾配の一次モーメント（平均）と二次モーメント（分散）を利用します。

一次モーメントの更新式：

$$m_t = \beta_1 m_{t-1} + (1 – \beta_1) g_t$$

バイアス補正された一次モーメント：

$$\hat{m}_t = \frac{m_t}{1 – \beta_1^t}$$

二次モーメントの推定値：

$$v_t = \beta_2 v_{t-1} + (1 – \beta_2) g_t^2$$

バイアス補正を考慮した推定値：

$$\hat{v}_t = \frac{v_t}{1 – \beta_2^t}$$

重みの更新式

$$θ_{t+1} = θ_t – \alpha \frac{\hat{m}}{\sqrt{\hat{v} + \epsilon}}$$

今回は下記の二乗誤差（または二乗損失）と呼ばれる損失関数の一例を使ってAdamでパラメータ更新を行ってみます。この関数は最適化問題を理解する際によく用いられる関数です。

$J(θ)=θ^2$

import numpy as np
import matplotlib.pyplot as plt

# 損失関数の定義
def J(theta):
    return theta**2

# 勾配の定義
def gradient(theta):
    return 2 * theta

# Adamオプティマイザーのパラメータ
theta = 10.0  # 初期値
eta = 0.1     # 学習率
beta1 = 0.9
beta2 = 0.999
epsilon = 1e-8
m = 0
v = 0
theta_values = [theta]

for t in range(1, 21):
    g = gradient(theta)
    m = beta1 * m + (1 - beta1) * g
    v = beta2 * v + (1 - beta2) * (g ** 2)
    m_hat = m / (1 - beta1 ** t)
    v_hat = v / (1 - beta2 ** t)
    theta = theta - eta * m_hat / (np.sqrt(v_hat) + epsilon)
    theta_values.append(theta)

# 損失関数のグラフ
theta_range = np.linspace(-12, 12, 400)
plt.plot(theta_range, J(theta_range), label='J(theta)')
plt.scatter(theta_values, [J(t) for t in theta_values], color='red')
plt.title('Adam OptimizerによるJ(theta) = theta^2の最小化')
plt.xlabel('theta')
plt.ylabel('J(theta)')
plt.legend()
plt.grid(True)
plt.show()

print(f"最終的なtheta: {theta:.5f}")

最終的なtheta: 8.02666

正則化

過学習防止のためのL1・L2正則化の紹介

例題：L1正則化とL2正則化を用いて回帰モデルを訓練し、その効果を比較する。

計算例：Lasso回帰（L1正則化）とリッジ回帰（L2正則化）を実装。

from sklearn.linear_model import LinearRegression, Lasso, Ridge
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt

# サンプルデータの生成
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X[:, 0] + np.random.randn(100)

# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# 通常の線形回帰
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_pred_lin = lin_reg.predict(X_test)

# Lasso回帰（L1正則化）
lasso = Lasso(alpha=0.1)
lasso.fit(X_train, y_train)
y_pred_lasso = lasso.predict(X_test)

# リッジ回帰（L2正則化）
ridge = Ridge(alpha=0.1)
ridge.fit(X_train, y_train)
y_pred_ridge = ridge.predict(X_test)

# 結果のプロット
plt.scatter(X_test, y_test, color='black', label='Test Data')
plt.plot(X_test, y_pred_lin, color='blue', label='Linear Regression')
plt.plot(X_test, y_pred_lasso, color='green', label='Lasso Regression')
plt.plot(X_test, y_pred_ridge, color='red', label='Ridge Regression')
plt.title('正則化手法の比較')
plt.xlabel('Feature')
plt.ylabel('Target')
plt.legend()
plt.show()

# パラメータの比較
print("通常の線形回帰の係数:", lin_reg.coef_)
print("Lasso回帰の係数:", lasso.coef_)
print("Ridge回帰の係数:", ridge.coef_)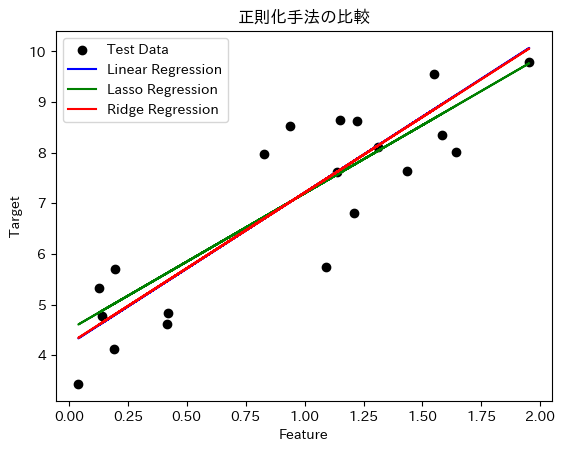

通常の線形回帰の係数: [2.99990042]
Lasso回帰の係数: [2.69828312]
Ridge回帰の係数: [2.98863263]

L1とL2の違い：L1正則化（Lasso）は係数をよりスパースにし、特徴量選択の効果があります。L2正則化（Ridge）は係数を小さく抑え、モデルの複雑さを制御します。

学習の振り返りと次回予告

今回は、確率統計と最適化手法が機械学習にどのように応用されるかを具体的な計算例とPythonコードを通じて学びました。確率統計はデータの不確実性をモデル化し、最適化手法はモデルのパラメータを効果的に調整するために不可欠です。これらの数学的基礎を理解することで、機械学習アルゴリズムの設計や解析がより深く行えるようになります。

次回は「情報理論と離散数学、さらなる数学的概念の応用」について探求します。情報理論はデータの情報量やエントロピーを扱い、離散数学はグラフ理論や組み合わせ論を通じて機械学習の複雑な問題にアプローチします。お楽しみに！