【第9回】ディープラーニングの基礎とCNNの仕組み（中編)

機械学習
2024.12.26
  1. 目的
    1. 【今回の主な内容】バッチ処理・最適化アルゴリズム
    2. 今回の学習の目標
    3. 前回の振り返り
  2. バッチ学習とオンライン学習
    1. オンライン学習と人間の脳の類似点
    2. バッチ学習と人間の脳の類似点
    3. 「オンライン学習」「バッチ学習」「ミニバッチ学習」の違い
      1. オンライン学習（Online Learning）
        1. オンライン学習の実装例
      2. バッチ学習（Batch Learning）
        1. バッチ学習の実装例
  3. ミニバッチ学習
    1. ミニバッチ学習と人間の脳の類似点
      1. ミニバッチ学習（Mini-Batch Learning）
      2. バッチサイズの調整方法
        1. 実験的にバッチサイズを調整
        2. 学習率とバッチサイズのスケーリング
          1. バッチサイズが学習に与える影響
        3. ミニバッチ学習の実装例
  4. GPU並列処理の活用術
    1. GPU並列処理の仕組み
    2. GPUの有効化と設定
      1. NVIDIA GPUの有効化と設定
      2. Apple Silicon GPUの有効化と設定
      3. Intel GPUの有効化と設定
        1. GPU活用のベストプラクティス（Apple Silicon）
  5. バッチ正規化 (Batch Normalization)
    1. バッチ正規化の背景と目的
      1. バッチ正規化の処理ステップと数式
        1. バッチ正規化のメリット
        2. バッチ正規化の図解
      2. 他の正規化手法との違い
        1. バッチ正規化
        2. レイヤー正規化
        3. インスタンス正規化
        4. グループ正規化
  6. 最適化アルゴリズムの選択と活用
    1. 最適化アルゴリズムとは？
      1. 最適化アルゴリズムの紹介（最急降下法・SGD）
      2. Momentum
      3. AdaGrad
      4. RMSprop
    2. Adam
      1. AdamW
    3. AdaBelief (2020)
    4. RAdam (2019)
    5. LookAhead Optimizer(2019)
    6. Ranger (2019)
    7. Lamb (2019)
    8. Sophia (2023)
    9. 学習率の調整
      1. コサインスケジューラー
      2. 線形スケジューラー
  7. データ拡張による汎化性能の向上
    1. データ拡張とは？
      1. 画像の回転 (Rotation)
      2. 平行移動 (Translation)
      3. 反転 (Flipping)
      4. ズーム (Scaling/Zooming)
      5. 色調変化 (Color Jittering)
      6. 切り抜き (Cropping)
  8. 正則化手法による汎化性能の向上
    1. L２正則化
    2. ドロップアウト
    3. 様々なドロップアウトの手法
      1. SpatialDropout
      2. Variational Dropout（変分ドロップアウト）
      3. DropConnect
      4. Concrete Dropout
      5. AlphaDropout
        1. 活性化関数としてのSELU
          1. 重みの初期化（LeCun正規化）
      6. Zoneout
  9. 学習プロセスの制御と改善
    1. 蒸留
    2. 蒸留の派生アルゴリズムと類似法
      1. FitNets
      2. Attention Transfer (AT)
      3. Soft Targets
      4. RKD
      5. CRD
      6. Self-Distillation（自己蒸留）
      7. TinyTL (Tiny Transfer Learning)
      8. Data-Free Knowledge Distillation（DFKD）
    3. 枝刈り（Pruning）
      1. 要素レベルの Pruningの実装例
      2. 構造化 Pruningの実装例
      3. 動的 Pruningの実装例
        1. Puring（枝刈り）に類似したモデル
    4. 量子化
      1. PTQの実装例
        1. 様々な量子化モデル
        2. 最近の研究からのモデル
    5. Early Stopping（早期終了）
        1. Early Stopping の派生手法と関連手法
    6. 学習の振り返りと次回予告

目的

このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用できる力を養うことが目的です。この過程で、実践的な演習やプロジェクトを通じて、手を動かしながら学ぶ姿勢を大切にしていきます。

【今回の主な内容】バッチ処理・最適化アルゴリズム

今回のテーマでは、「効率的な学習」を実現するために欠かせない バッチ処理 と 最適化アルゴリズム の基礎に焦点を当てます。これらは、ディープラーニングモデルが高次元で膨大なデータを効率よく処理し、実用的な性能を獲得するための土台です。学習プロセスを通じて、ニューロンの結合強度を意味する「重み」がどのように最適化されるかを理解することは、より精密で効果的なモデル構築に直結します。

今回の学習の目標

ディープラーニングモデルの学習プロセスを効果的に設計・実行するためのテクニックを深く理解し、実践に活用できるスキルを習得することを目指します。特に、モデルの性能や汎化能力を向上させる学習アルゴリズムやトレーニングテクニックを体系的に学びます。以下の4つのポイントを柱に、効率的かつ安定した学習方法を習得します。

  1. バッチ処理とバッチ正規化の活用
    • ミニバッチ学習
      • データを小さなバッチに分割し、計算リソースの効率的活用と学習の安定性を実現します。バッチサイズの選定がモデルの学習速度や性能に与える影響についても学びます。
    • GPU並列処理
      • GPUの高速並列処理能力を活用して、バッチ処理を効率化します。大規模データセットの学習時間短縮と計算資源の最適活用を目指します。
    • バッチ正規化（Batch Normalization）
      • 各バッチ内でデータを正規化することで、勾配消失問題を緩和し、学習速度と収束の安定性を向上させます。
  2. 最適化アルゴリズムの選択と活用
    • 確率的勾配降下法（SGD）とその派生手法
      • SGDの基礎を学び、MomentumやAdamなどの派生手法が収束速度や勾配の安定性にどのように寄与するかを解説します。これらのアルゴリズムを実践的に選択し、適用する技術を身につけます。
    • 学習率の調整
      • 学習率の適切な設定が収束性やモデル性能に与える影響を理解し、ステップスケジューラーやコサインスケジューラーを用いた動的な調整手法を実践します。
  3. データ拡張と正則化による汎化性能の向上
    • データ拡張
      • 画像の回転、平行移動、反転、ズームなどのテクニックを用いてデータセットを拡張し、モデルの過学習を防ぎます。
    • 正則化手法
      • L1/L2正則化やドロップアウトを活用して、モデルの複雑さを制御しつつ汎化性能を向上させる実践的なスキルを習得します。
  4. 学習プロセスの制御と改善
    • 蒸留（Knowledge Distillation）
      • 大規模なティーチャーモデルから小規模なスチューデントモデルへ知識を転移し、モデルの軽量化を図ります。
    • 枝刈り（Pruning）
      • 不要なパラメータや接続を削減して計算量を抑え、推論速度を向上させる手法を学びます。
    • 量子化（Quantization）
      • モデルパラメータを低精度フォーマットに変換することで、メモリ使用量の削減と推論速度の向上を実現します。
    • Early Stopping（早期終了）
      • 検証データの損失が一定期間改善しない場合に学習を停止することで、過学習の防止と計算リソースの効率的利用を実現します。

ゴール

  • 最適なトレーニングループ構築
    • 最適化アルゴリズムやバッチ処理を活用して、効率的で安定した学習プロセスを設計します。
  • 汎化性能の向上
    • データ拡張や正則化手法を駆使し、未知データへの対応力を高めます。
  • 計算効率の最適化
    • GPU並列処理とモデルの軽量化技術を組み合わせて、トレーニングと推論の効率化を実現します。
  • 過学習の防止
    • Early Stoppingなどの手法を活用し、モデルの性能を最大化しつつ無駄なリソース消費を防ぎます。
  • 次回の学びへの応用力強化
    • 得られた知識を基盤として、さらなる高度なトレーニング手法やモデル設計に進む準備を整えます。

前回の振り返り

ディープラーニングは、私たちの脳のニューロンとその相互作用を模倣したニューラルネットワークを通じて、データから学び、複雑な問題を解決する技術です。これまでの学びでは、ディープラーニングの基本構造や、誤差逆伝播法による重みの調整の仕組みについて深く掘り下げました。そして前回は、損失関数と活性化関数がどのように学習を導く役割を果たすかを探りました。

【前回のブログ】

【第9回】ディープラーニングの基礎とCNNの仕組み（前編)
目的 このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用...
shion.blog
2024.11.23

モデル学習の基本プロセス

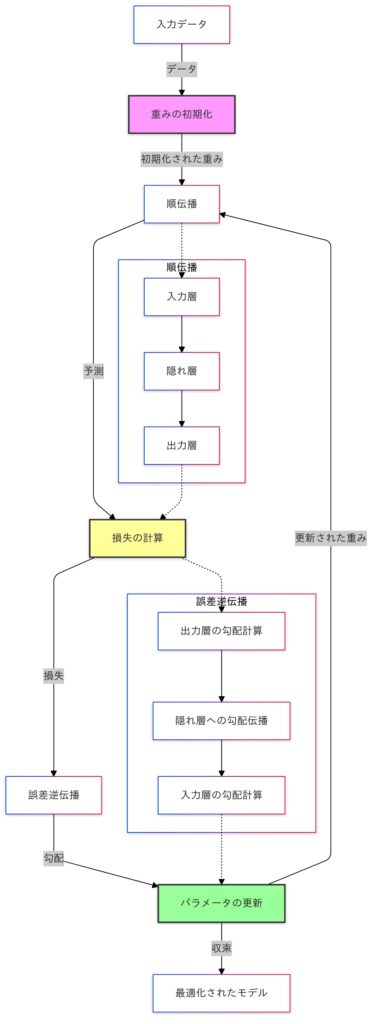
  1. 入力データ: モデルのトレーニングは、入力データの提供から始まります。
  2. 重みの初期化: ネットワーク内のパラメータ（重みとバイアス）がランダムに初期化されます。
  3. 順伝播: データは、入力層から隠れ層、出力層へと伝播され、予測値が生成されます。
  4. 損失の計算: 予測値と実際の値との差異（損失）を計算します。
  5. 誤差逆伝播: 損失を基に勾配を計算し、誤差を出力層から入力層まで逆方向に伝播します。
  6. パラメータの更新: 勾配を用いて重みを更新し、モデルを最適化します。

このプロセスを繰り返すことで、モデルは徐々に精度を向上させ、最適化されたネットワークが得られます。この図は、ディープラーニングにおけるモデル学習の全体像を簡潔に示しています。

バッチ学習とオンライン学習

ディープラーニングモデルの学習を効率化し、精度を向上させる鍵となる技術に「バッチ処理」があります。膨大なデータを扱う場面で、すべてのデータを一度に処理するのではなく、バッチ（小分けのデータ）に分割することで、計算リソースを効率的に活用します。まずはそれぞれの学習方法と人間の脳の類似点について考えてみましょう。

オンライン学習と人間の脳の類似点

オンライン学習は、データを逐次処理し、新しい情報を学びながらモデルを更新する手法です。これは、人間の脳が日常生活で行う逐次学習と非常に似ています。たとえば、会話中に相手の意図を理解しながら新しい知識を得たり、仕事中に発生した問題を解決しながらスキルを学んだりするプロセスが該当します。脳は一度に全情報を学習するのではなく、得られる情報をリアルタイムで処理し、必要に応じて適応的に更新していきます。また、オンライン学習は過去のデータにとらわれず、新しいデータに基づいて柔軟に判断するため、環境の変化に対応する脳の適応力とも共通します。一方で、ノイズの多い情報に影響を受けやすい点は、人間の判断の揺らぎとも関連しています。

バッチ学習と人間の脳の類似点

バッチ学習は、大量のデータを一括処理して学習する手法であり、人間の脳が行う記憶統合や集中学習と似ています。たとえば、脳は睡眠中に日中の経験を整理し、重要な情報を長期記憶として保存します。この過程では、大量の情報を一度にまとめて処理し、全体のパターンや関係性を見出します。また、試験前に集中して学ぶような場面でも、大量の知識を短期間で吸収し、統合的に理解するプロセスはバッチ学習の一括処理と共通しています。ただし、バッチ学習はリアルタイム性がなく、計算リソースを大量に必要とするため、エネルギー効率に優れた脳の動きとは異なります。それでも、大局的な学習能力という点で、人間の脳とバッチ学習は共通性を持っています。

「オンライン学習」「バッチ学習」「ミニバッチ学習」の違い

まずはそれぞれの学習の違いを見ていきましょう。

手法特徴使用シナリオ数式
オンライン学習データを逐次処理。リアルタイム性が高いが、勾配が不安定になる可能性。ストリーミングデータの処理（例：株価予測）。$ L = l(y_t, \hat{y}_t)$
バッチ学習データ全体を一括で処理。計算精度が高いが、リソース消費が大きい。画像分類タスクなど、大量のデータが事前に揃っている場合。$ L =$$ \frac{1}{N} \sum_{i=1}^{N} l(y_i, \hat{y}_i)$
ミニバッチ学習バッチサイズでトレードオフを取りつつ処理を効率化。一般的なディープラーニングのトレーニングで主流。$ L =$$ \frac{1}{B} \sum_{i=1}^{B} l(y_i, \hat{y}_i)$

オンライン学習（Online Learning）

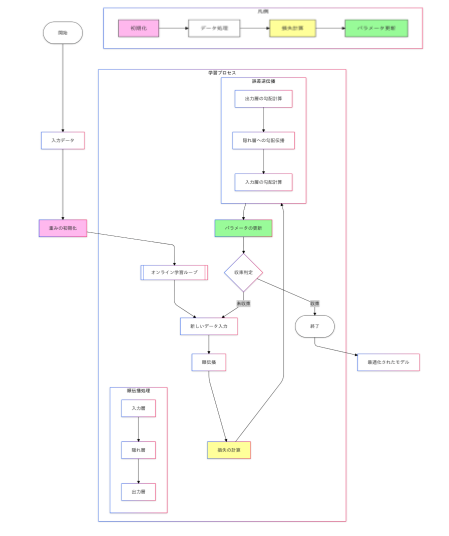
データ処理方法：

データが1つずつ（または少量ずつ）リアルタイムに与えられ、それに応じてモデルが逐次更新されます。

特徴：

  • リアルタイム性
    • 新しいデータが到着するたびにモデルを更新可能。
  • リソース効率
    • 一度に処理するデータ量が少ないため、メモリ消費が少ない。
  • デメリット
    • 勾配が不安定になりやすい。
    • ノイズの多いデータに過剰適応（過学習）しやすい。

使用例：

  • 株価予測システム
    • ストリーミングデータを用い、次の瞬間の株価を予測。
  • リアルタイムチャットボット
    • 会話ログを使って即時にモデルを更新。

損失関数：オンライン学習の損失関数は単一データ点に基づいて計算されます。

$$ L = l(y_t, \hat{y}_t)$$

$y_t​$は真のラベル。$\hat{y}_t$はモデルの予測。

利点と課題

  • 利点
    • データが随時到着するシステムに適している。
    • リアルタイムでモデルを更新可能。
  • 課題
    • 勾配の不安定性が原因で、収束が遅くなる場合がある。
    • 過去のデータ情報を効率的に保持する仕組みが必要（例: メモリ効率の良い勾配保存法）。
オンライン学習の実装例

PyTorchを使用して線形回帰モデルを使ってオンライン学習（逐次学習）でトレーニングする例を実装してみます。PyTorchを使った詳細説明も行いますので手を動かせる場合は手を動かして実際にコードを記述して学んでみてください。

データセットはカリフォルニア州の住宅価格に関するデータセットを使います。

ライブラリのインポート

import torch
import torch.nn as nn
import torch.optim as optim
import random
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split

非線形モデルの定義の定義

class NonLinearRegressionModel(nn.Module):
    def __init__(self):
        super(NonLinearRegressionModel, self).__init__()
        self.fc1 = nn.Linear(8, 64)  # 8入力、64出力
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(64, 1)  # 64入力、1出力

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x

ここではnn.Module を継承することで、PyTorchのモデルとして動作するための基本的な機能を持つことができます。

  • super(LinearRegressionModel, self).__init__() は、親クラス（nn.Module）のコンストラクタを呼び出しています。これにより、親クラスの初期化処理が行われます。
  • self.fc1 = nn.Linear(8, 64) は、8つの入力ユニットと64の出力ユニットを持つ全結合層（線形層）を定義しています。
  • self.fc2 = nn.Linear(64, 1) は、64の入力ユニットと1つの出力ユニットを持つ全結合層（線形層）を定義しています。
  • forward メソッドは、順伝播（フォワードパス）を定義しています。このメソッドは、入力データ x を受け取り、モデルの出力を計算します。

データセットの読み込みと前処理

# データセットの読み込み
housing = fetch_california_housing()
X, y = housing.data, housing.target

# データをpandasのDataFrameに変換
df = pd.DataFrame(X, columns=housing.feature_names)
df['target'] = y

# NaN値を削除
df = df.dropna()

# 特徴量とターゲットに分割
X = df.drop('target', axis=1).values
y = df['target'].values

# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# データをPyTorchのテンソルに変換
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32).view(-1, 1)
y_test = torch.tensor(y_test, dtype=torch.float32).view(-1, 1)

このコードでは前処理を行い、PyTorchのテンソルに変換する一連の手順を示しています。データセットの読み込み、標準化、データの分割、テンソルへの変換を行うことで、モデルのトレーニングと評価に使用できるデータを準備します。これにより、PyTorchを使用して線形回帰モデルをオンライン学習でトレーニングする準備が整います。

PyTorchのテンソル変換の説明

  • torch.tensor 関数を使用して、NumPy配列をPyTorchのテンソルに変換します。
  • dtype=torch.float32 は、データ型を32ビット浮動小数点数に指定します。
  • view(-1, 1) は、ターゲットデータ y_train と y_test を2次元テンソルに変換します。ここで、-1 は自動的に適切なサイズに調整されることを意味します。
  • つまり、y_train と y_test データに対して .view(-1, 1) を使用して2次元テンソルに変換する理由は、PyTorchの線形回帰モデルが期待するターゲットデータの形状に合わせるためです。具体的には、PyTorchの nn.Linear レイヤーは、入力データとターゲットデータが特定の形状を持つことを期待しています。
  • 入力データ (X_train, X_test) の形状：
    • X_train と X_test は、各サンプルが複数の特徴量を持つ2次元テンソルです。例えば、X_train の形状は (num_samples, num_features) です。ここで、num_samples はサンプルの数、num_features は特徴量の数を示します。
  • ターゲットデータ (y_train, y_test) の形状：
    • y_train と y_test は、各サンプルに対して1つのターゲット値を持つ必要があります。これを2次元テンソルとして表現するために、形状を (num_samples, 1) に変換します。
    • .view(-1, 1) を使用することで、1次元のターゲットデータを2次元テンソルに変換します。ここで、-1 は自動的に適切なサイズに調整されることを意味し、1 は各サンプルに対して1つのターゲット値を持つことを示します。

モデル、損失関数、最適化アルゴリズムの初期化

model = NonLinearRegressionModel()
criterion = nn.MSELoss()  # 平均二乗誤差損失
optimizer = optim.SGD(model.parameters(), lr=0.01)
  • LinearRegressionModel クラスは、PyTorchの nn.Module を継承しています。
  • nn.MSELoss() は、予測値と実際の値の間の平均二乗誤差を計算するための損失関数です。
  • optim.SGD は、PyTorchの最適化アルゴリズムの一つで、モデルのパラメータを更新するために使用されます。

オンライン学習ループ

# オンライン学習ループの開始
for step in range(1000):  # 1000回更新を想定
    # ランダムなデータポイントの選択
    idx = random.randint(0, X_train.shape[0] - 1)
    x, y = X_train[idx].view(1, -1), y_train[idx].view(1, -1)

    # モデルの予測
    y_pred = model(x)
    # 損失の計算
    loss = criterion(y_pred, y)
    # 勾配のリセット
    optimizer.zero_grad()
    # バックプロパゲーション:勾配の計算とパラメータの更新
    loss.backward()
    # パラメータの更新
    optimizer.step()

    # ログ出力と評価
    if step % 100 == 0:  # 100ステップごとにログを出力
        # 評価
        model.eval()  # 評価モード
        with torch.no_grad():
            Y_train_pred = model(X_train).view(-1).tolist()
            Y_test_pred = model(X_test).view(-1).tolist()
            
            # NaN値のチェック
            if np.any(np.isnan(Y_train_pred)) or np.any(np.isnan(Y_test_pred)):
                print(f"NaN values found at step {step}")
                break
            
            r2_train = r2_score(y_train, Y_train_pred)
            r2_test = r2_score(y_test, Y_test_pred)
        model.train()  # 訓練モードに戻す

        print(f"Step {step}: Loss = {loss.item()}, R-squared (Train) = {r2_train}, R-squared (Test) = {r2_test}")
Step 0: Loss = 1.497462272644043, R-squared (Train) = -2.8930491520356845, R-squared (Test) = -2.8979675132366345
Step 100: Loss = 0.11681777238845825, R-squared (Train) = 0.2683064067169121, R-squared (Test) = 0.20201395903497776
...
Step 700: Loss = 0.38664156198501587, R-squared (Train) = 0.25707681839085983, R-squared (Test) = 0.10102724438822674
Step 800: Loss = 0.44846442341804504, R-squared (Train) = 0.6007633390263472, R-squared (Test) = 0.5709814493083019
Step 900: Loss = 1.531463384628296, R-squared (Train) = 0.5758513261169051, R-squared (Test) = 0.5419270109690251
  1. オンライン学習ループの開始:
    • 1000回の更新を想定してオンライン学習を行います。range(1000) は、0から999までの整数を生成します。
  2. ランダムなデータポイントの選択:
    • トレーニングデータからランダムに1つのデータポイントを選択します。random.randint(0, X_train.shape[0] - 1) は、トレーニングデータからランダムに1つのデータポイントのインデックスを選択し、選択されたインデックスに対応する入力データ(X_train[idx]) とターゲットデータ(y_train[idx])を取得します。
  3. モデルの予測:
    • モデルを使用して、入力データ x に対する予測値 y_pred を計算します。
  4. 損失の計算:
    • 損失関数を使用して、予測値 y_pred と実際の値 y の間の損失 loss を計算します。
  5. 勾配のリセット:
    • 前回の勾配をリセットします。これにより、前回の勾配が次の計算に影響を与えないようにします。
  6. バックプロパゲーション:
    • 損失 loss に基づいて勾配を計算します。
  7. パラメータの更新:
    • 計算された勾配を使用して、モデルのパラメータを更新します。
  8. ログ出力と評価:
    • 100ステップごとにログを出力し、モデルの性能を評価します。
    • model.eval() は、モデルを評価モードに切り替えます。これにより、ドロップアウトやバッチ正規化などのレイヤーが評価モードで動作します。
    • with torch.no_grad() ブロック内では、勾配計算を無効にします。これにより、評価時の計算が効率的になります。
    • r2_score(y_test, Y_pred) を使用して、決定係数（R-squared）を計算します。R-squared は、モデルの予測性能を評価する指標です。
    • np.any(np.isnan(Y_train_pred)) と np.any(np.isnan(Y_test_pred)) を使用して、予測値に NaN 値が含まれているかどうかをチェックします。NaN 値が含まれている場合、エラーメッセージを出力し、ループを終了します。
    • import pandas as pd
    • model.train() は、モデルを訓練モードに戻します。
    • print(f"Step {step}: Loss = {loss.item()}, R-squared (Train) = {r2_train}, R-squared (Test) = {r2_test}") は、現在のステップ、損失、トレーニングデータとテストデータの決定係数をログに出力します。
  • 決定係数について
状況説明判断基準
トレーニングデータの決定係数が高く、テストデータの決定係数が低い過学習が発生している可能性が高い。モデルがトレーニングデータに過度に適合しており、テストデータでの汎化性能が低い。
トレーニングデータとテストデータの決定係数がほぼ同じ過学習が発生していないと考えられる。モデルがデータ全体の分散を適切に説明しており、汎化性能が高い。
トレーニングデータとテストデータの決定係数がどちらも低いモデルがデータを十分に学習できていない可能性がある（アンダーフィットの可能性）。モデルの容量不足、特徴量不足、または不適切なハイパーパラメータが原因。


最終的なモデルのパラメータを出力

for name, param in model.named_parameters():
    print(f"{name}: {param.data}")
fc1.weight: tensor([[ 0.1038, -0.2549, -0.2534, -0.2532, -0.2381, -0.0308, -0.2129, -0.0486],
        [-0.2793,  0.0695, -0.1803,  0.3256, -0.2593,  0.3121, -0.1401, -0.2626],
        [ 0.0227, -0.2128,  0.0705, -0.2593,  0.3119, -0.0848,  0.3080,  0.2504],
...
          0.1933,  0.4457, -0.2168,  0.3370, -0.1079,  0.1026,  0.2219,  0.1265,
          0.0422,  0.0718, -0.1204, -0.0770, -0.0084,  0.1158, -0.0554,  0.1743,
          0.0972, -0.0305, -0.0323,  0.0205, -0.0200, -0.1119,  0.1084,  0.0947]])
fc2.bias: tensor([0.9751])

8つの入力値の重みとバイアスはオンライン学習を経て更新され、最終的な値が出力されます。

  • model.named_parameters() は、モデルの全てのパラメータ（重みとバイアス）とその名前を取得します。
  • param.data は、パラメータの値を取得します。param はPyTorchのテンソルであり、data 属性を使用してその値を取得します。

バッチ学習（Batch Learning）

データ処理方法：

全データを一括で処理し、損失を計算してからパラメータを更新します。

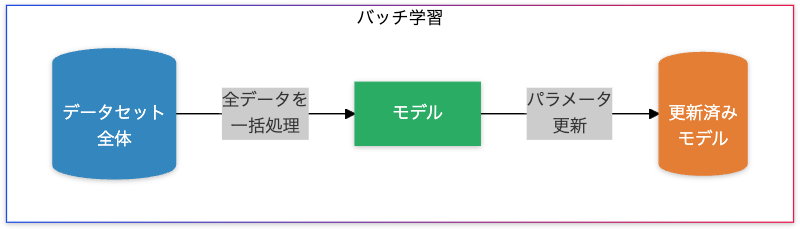
特徴

  • 精度が高い勾配計算
    • 全データを使用するため、勾配の推定が正確。
  • デメリット
    • 必要なメモリ量が膨大。
    • データ量が増えると計算コストが急増。

使用例：

  • 画像分類タスク
    • データセット全体を使い、精密な分類モデルを構築。
  • 文書分類
    • 固定された大量のデータセットを一括で学習。

損失関数：バッチ学習では、データ全体にわたる平均損失が計算されます。

$$ L = \frac{1}{N} \sum_{i=1}^{N} l(y_i, \hat{y}_i)$$

$N$：データの総数。

利点と課題

  • 利点
    • 正確な勾配計算により、安定した収束が期待できる。
  • 課題
    • 計算資源の制約が大きく、リアルタイム性には適さない。
    • データセット全体を収集しておく必要がある。
バッチ学習の実装例

今回はIrisのデータセットを使ってバッチ学習の実装を行います。Irisのデータセットは150サンプルしかなく、非常に小さいデータセットであるため、全てのデータを一度にメモリにロードして処理することが容易であり、バッチ学習が適していると言えます。

ライブラリのインポート

import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

シンプルな非線形分類モデル（多層パーセプトロン）の定義

class NeuralNetworkModel(nn.Module):
    def __init__(self, input_dim):
        super(NeuralNetworkModel, self).__init__()
        self.model = nn.Sequential(
            nn.Linear(input_dim, 64),    # 入力層から隠れ層1
            nn.ReLU(),                    # 活性化関数
            nn.Linear(64, 32),            # 隠れ層1から隠れ層2
            nn.ReLU(),                    # 活性化関数
            nn.Linear(32, 3)              # 隠れ層2から出力層（3クラス分類）
        )
    
    def forward(self, x):
        return self.model(x)
  • super(NeuralNetworkModel, self).__init__() は、親クラス（nn.Module）のコンストラクタを呼び出しています。これにより、親クラスの初期化処理が行われます。
  • self.model = nn.Sequential(...) は、モデルの層を順番に定義するためのコンテナです。nn.Sequential を使用することで、層を順番に適用することができます。
  • nn.Linear(input_dim, 64) は、入力層から最初の隠れ層への全結合層（線形層）を定義しています。input_dim は入力の次元数、64 は隠れ層のユニット数です。
  • nn.ReLU() は、ReLU（Rectified Linear Unit）活性化関数を定義しています。これは、非線形性を導入するために使用されます。
  • nn.Linear(64, 32) は、最初の隠れ層から次の隠れ層への全結合層を定義しています。64 は前の層のユニット数、32 は次の隠れ層のユニット数です。
  • nn.Linear(32, 3) は、最後の隠れ層から出力層への全結合層を定義しています。32 は前の層のユニット数、3 は出力のクラス数です（Irisデータセットの場合、3クラス分類）。

データの読み込みと前処理

アイリスのデータセットを読み込み、データの標準化、データの分割を行います。

iris = load_iris()
X = iris.data
y = iris.target

# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# データの分割
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.2, random_state=42, stratify=y
)

データをPyTorchのテンソルに変換

X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.long)
y_test = torch.tensor(y_test, dtype=torch.long)

デバイスの設定

GPUが利用可能な場合はGPUを使用し、そうでない場合はCPUを使用します。

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f'Using device: {device}')

モデル、損失関数、最適化アルゴリズムの初期化

このコードは、モデル、損失関数、および最適化アルゴリズムの初期化を行っています。

input_dim = X_train.shape[1]
model = NeuralNetworkModel(input_dim).to(device)
criterion = nn.CrossEntropyLoss()  # クロスエントロピー損失
optimizer = optim.Adam(model.parameters(), lr=0.001)  # Adamオプティマイザ
  • X_train.shape[1] は、トレーニングデータの特徴量の数を取得します。
  • input_dim には、Irisデータセットの特徴量の数（4）が格納されます。
  • NeuralNetworkModel クラスのインスタンスを作成します。input_dim は入力層の次元数を指定します。
  • nn.CrossEntropyLoss は、分類タスクにおいてよく使用される損失関数です。クロスエントロピー損失は、モデルの予測と実際のラベルとの間の誤差を計算します。
  • この損失関数は、ソフトマックス関数と負の対数尤度損失を組み合わせたもので、多クラス分類タスクに適しています。https://shion.blog/the-9th-machine-learning-workshop_1/#toc43

データをデバイスに転送

このコードは、トレーニングデータとテストデータを指定されたデバイス（GPUまたはCPU）に転送する処理を行っています。これにより、データがモデルと同じデバイス上で処理されるようになります。

X_train = X_train.to(device)
y_train = y_train.to(device)
X_test = X_test.to(device)
y_test = y_test.to(device)

バッチ学習ループ

このコードは、Irisデータセットを使用してシンプルな多層パーセプトロン（MLP）モデルをバッチ学習でトレーニングする部分です。

# バッチ学習ループ
num_epochs = 100  # エポック数

for epoch in range(num_epochs):
    model.train()  # 訓練モード
    
    # 勾配をリセット
    optimizer.zero_grad()
    
    # モデルの予測
    outputs = model(X_train)
    
    # 損失の計算
    loss = criterion(outputs, y_train)
    
    # 勾配の計算とパラメータの更新
    loss.backward()
    optimizer.step()
    
    # ログ出力と評価
    if (epoch + 1) % 10 == 0:  # 10エポックごとにログを出力
        model.eval()  # 評価モード
        with torch.no_grad():
            # 訓練データの予測
            train_outputs = model(X_train)
            _, train_preds = torch.max(train_outputs, 1)
            accuracy_train = (train_preds == y_train).sum().item() / y_train.size(0)
            
            # テストデータの予測
            test_outputs = model(X_test)
            _, test_preds = torch.max(test_outputs, 1)
            accuracy_test = (test_preds == y_test).sum().item() / y_test.size(0)
        
        print(f"Epoch {epoch + 1}: Loss = {loss.item():.4f}, "
              f"Accuracy (Train) = {accuracy_train:.4f}, "
              f"Accuracy (Test) = {accuracy_test:.4f}")
Using device: cpu
Epoch 10: Loss = 0.9473, Accuracy (Train) = 0.8083, Accuracy (Test) = 0.8000
Epoch 20: Loss = 0.7984, Accuracy (Train) = 0.8583, Accuracy (Test) = 0.8000
Epoch 30: Loss = 0.6504, Accuracy (Train) = 0.8833, Accuracy (Test) = 0.7667
Epoch 40: Loss = 0.5238, Accuracy (Train) = 0.8667, Accuracy (Test) = 0.8000
Epoch 50: Loss = 0.4285, Accuracy (Train) = 0.8750, Accuracy (Test) = 0.8000
Epoch 60: Loss = 0.3594, Accuracy (Train) = 0.8917, Accuracy (Test) = 0.7667
Epoch 70: Loss = 0.3056, Accuracy (Train) = 0.9250, Accuracy (Test) = 0.8333
Epoch 80: Loss = 0.2603, Accuracy (Train) = 0.9250, Accuracy (Test) = 0.8667
Epoch 90: Loss = 0.2193, Accuracy (Train) = 0.9250, Accuracy (Test) = 0.9000
Epoch 100: Loss = 0.1821, Accuracy (Train) = 0.9583, Accuracy (Test) = 0.9000

最終的なモデルのパラメータを出力

for name, param in model.named_parameters():
    print(f"{name}: {param.data}")
model.0.weight: tensor([[ 5.3092e-01,  3.0507e-01, -3.2453e-01,  4.1645e-01],
        [-4.3171e-01,  3.9466e-01,  2.6941e-01,  2.2325e-01],
        [ 3.3881e-01, -5.1786e-01,  3.6361e-01, -3.1159e-01],
        [ 4.9230e-01, -1.9013e-01,  3.0597e-03, -3.6174e-01],
...
          0.2088, -0.0961,  0.1437,  0.1756, -0.1813, -0.2467, -0.1940, -0.0985,
          0.1204,  0.2737, -0.1081, -0.1735,  0.1655,  0.0301,  0.1918,  0.0942,
         -0.1395, -0.0965, -0.1541,  0.1781, -0.0656,  0.0986,  0.1466, -0.2550]])
model.4.bias: tensor([-0.1315,  0.1318, -0.1750])

ミニバッチ学習

ミニバッチ学習と人間の脳の類似点

ミニバッチ学習は、大量のデータを一度に処理するバッチ学習と、逐次処理を行うオンライン学習の中間的な手法です。人間の脳においては、段階的な学習や反復的なトレーニングに似ています。たとえば、スポーツや音楽の練習では、全体のスキルを一度に学ぶのではなく、部分的な動作を繰り返し練習して統合するアプローチがとられます。このように、分割された情報を効率的に処理し、それを統合的な理解に結びつけるプロセスが、ミニバッチ学習の分割処理と類似しています。また、ミニバッチ学習ではデータのランダム性を利用して多様なパターンを学ぶため、人間が異なる状況で知識を応用しながら学ぶ「経験の蓄積」にも対応します。一方で、バッチサイズ（学習単位）の選択による効果の違いは、人間の注意力や集中時間の変化と関連付けて考えられます。ミニバッチ学習は効率性と柔軟性を両立した学習法として、脳の段階的適応をうまく模倣しています。

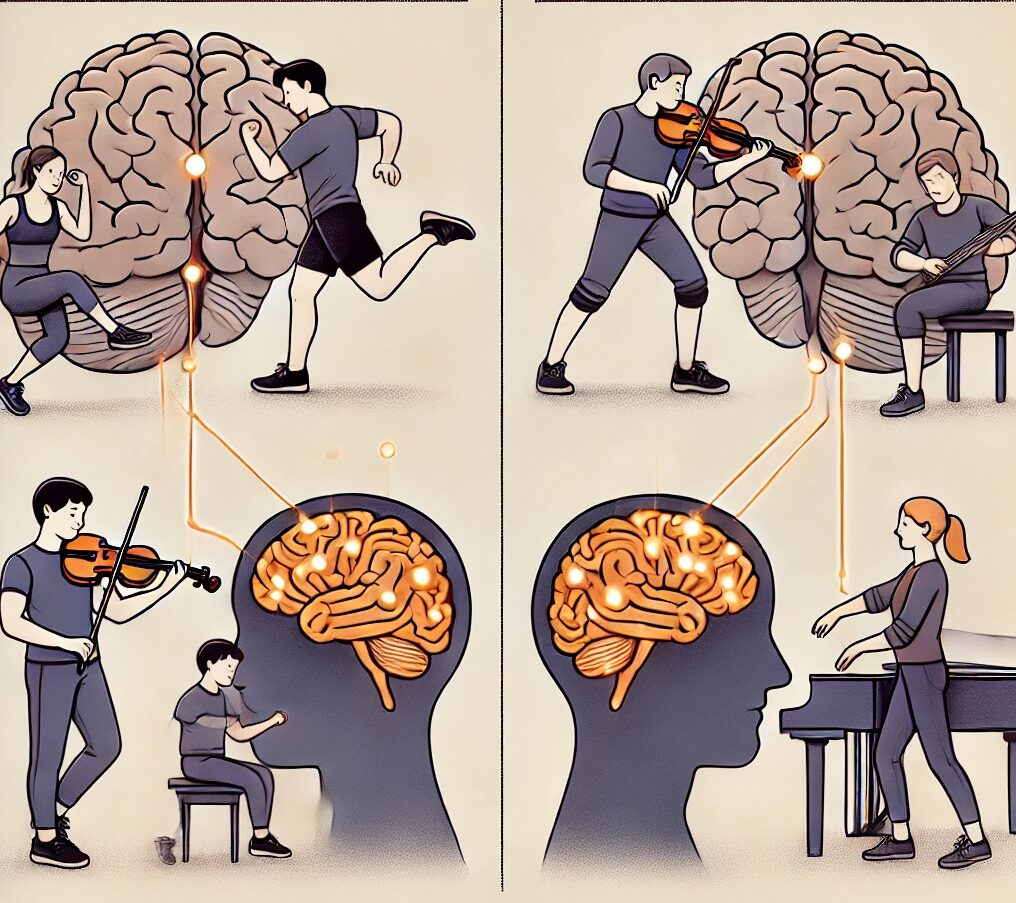
ミニバッチ学習（Mini-Batch Learning）

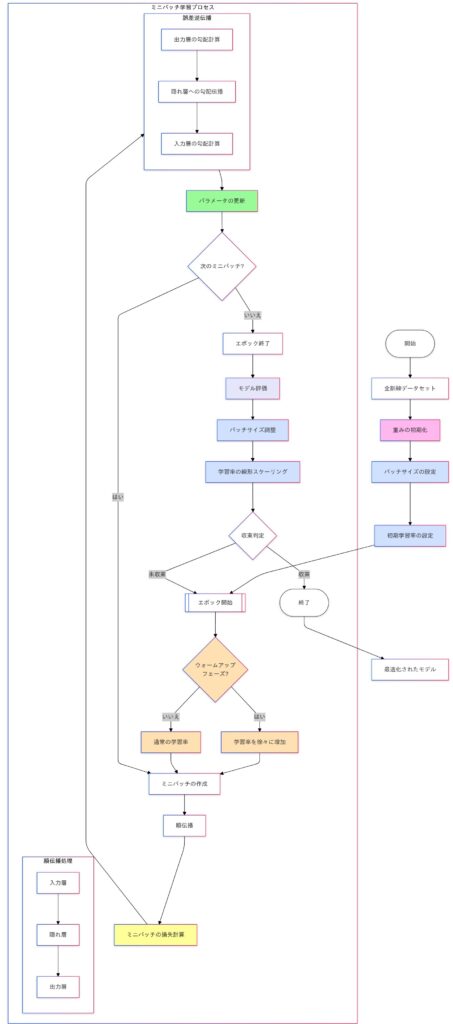
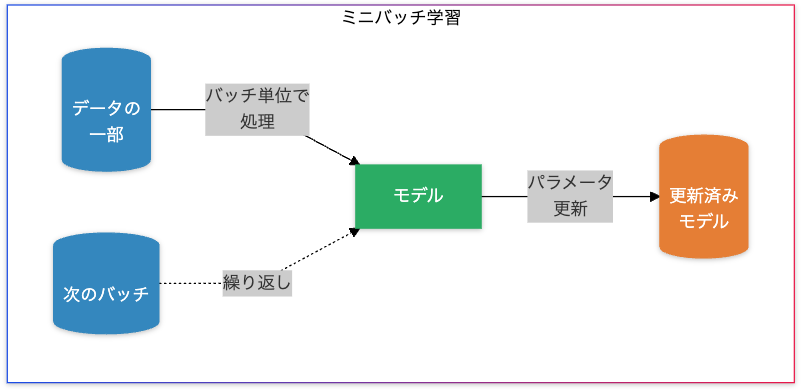
データ処理方法：

データを小さなバッチ（部分集合）に分割し、各バッチごとに損失を計算・更新します。

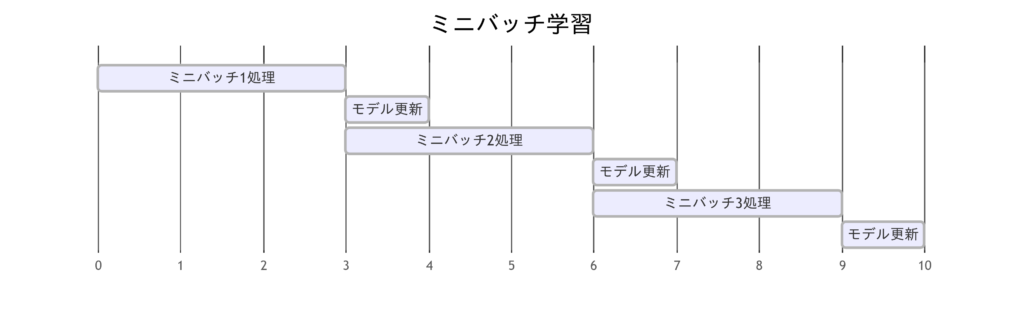
特徴：

  • トレードオフの優位性
    • バッチ学習とオンライン学習の中間的な方法。
  • 安定性と効率性
    • 小さなバッチにより、勾配計算の安定性と計算効率を両立。

使用例：

  • 一般的なディープラーニング：GPUの並列処理を活用する。
  • 大規模データセット：全体を処理せずとも学習可能。

損失関数：ミニバッチサイズ $B$ を用いた場合の損失関数は次のように表されます。

$$ L = \frac{1}{B} \sum_{i=1}^{B} l(y_i, \hat{y}_i)$$

$B$：バッチサイズ。

利点と課題

  • 利点
    • バッチサイズに応じた柔軟性。
    • 計算リソースの効率的利用。
  • 課題
    • 適切なバッチサイズの選択が必要（小さすぎると収束が不安定、大きすぎると一般化性能が低下）

バッチサイズの調整方法

実験的にバッチサイズを調整
バッチサイズ特徴メリットデメリット適用シナリオ
小さいサイズ（例: 16, 32）勾配ノイズが多く、モデル更新が頻繁。メモリ使用量が少ない。– メモリ効率が良い
– ロバスト性が向上する可能性- 小型GPUで処理可能		– 勾配ノイズが大きく、収束が不安定になる場合がある- 訓練時間が長くなる場合がある– 小型データセット
– モバイル環境や軽量モデルの訓練
中程度サイズ（例: 64, 128）小さすぎず、大きすぎないバランス。勾配のばらつきを抑えながらもメモリ使用量を節約。– トレードオフが最適化されやすい
– 訓練の安定性と速度のバランスが良い		– 最適化に調整が必要な場合がある– 一般的な設定
– モデルの検証段階
大きいサイズ（例: 256, 512）勾配のばらつきが少なく、計算効率が高い。ただし、メモリ消費が多い。– 計算効率が向上
– 勾配が安定し、収束がスムーズ		– 大型メモリが必要
– 局所解に陥るリスク
– 汎化性能が低下する場合がある		– 大型データセット
– ハイパフォーマンスGPU環境
非常に大きいサイズ（例: 1024以上）ほぼ完全なバッチ学習に近く、計算効率は最大。ただし汎化性能が大幅に低下するリスクがある。– 安定した勾配
– 効率的なGPU利用		– 過剰なメモリ使用量
– 過学習のリスクが高まる		– バッチ学習を意図した特殊なシナリオ
– 高性能サーバー環境

実験プロセス

  1. 小さいバッチサイズで開始:
    • 初期の収束挙動と勾配ノイズの影響を評価。
    • 訓練時間の長短を記録し、損失曲線の安定性を観察。
  2. 中程度のサイズを試す:
    • トレードオフのバランスを評価。
    • 初期学習率を調整し、収束の速度を観察。
  3. 大きいサイズでテスト:
    • 訓練の高速化を目指し、汎化性能を評価。
    • 訓練後、検証データで過学習がないかチェック。
  4. 性能の比較と最適化:
    • 損失曲線、収束速度、検証精度を比較して最適なサイズを選択。
学習率とバッチサイズのスケーリング

バッチサイズが大きくなるほど、学習率を適切に増加させる必要があります。これは、大きなバッチサイズでは計算される勾配がより安定するためです。

  • 線形スケーリングルール

$$\eta_{\text{new}} = \eta_{\text{original}} \times \frac{\text{batch size}_{\text{new}}}{\text{batch size}_{\text{original}}}$$

$η_{new​}$：新しい学習率、$η_{original}​$：元の学習率

実装例）

  • 元の学習率が 0.01 で、元のバッチサイズが 32、新しいバッチサイズが 128 の場合

$$\eta_{\text{new}} = 0.01 \times \frac{128}{32} = 0.04$$

# 学習率とバッチサイズをスケーリングする関数
def scale_learning_rate(original_lr, original_batch_size, new_batch_size):
    """
    学習率をバッチサイズに応じてスケーリングします。

    Parameters:
        original_lr (float): 元の学習率
        original_batch_size (int): 元のバッチサイズ
        new_batch_size (int): 新しいバッチサイズ

    Returns:
        float: 新しい学習率
    """
    return original_lr * (new_batch_size / original_batch_size)

# 元の学習率とバッチサイズ
original_lr = 0.01  # 元の学習率
original_batch_size = 32  # 元のバッチサイズ

# 新しいバッチサイズ
new_batch_size = 128

# 新しい学習率の計算
new_lr = scale_learning_rate(original_lr, original_batch_size, new_batch_size)

# 結果の表示
print(f"元の学習率: {original_lr}")
print(f"新しい学習率: {new_lr}")

結果の例）

元の学習率: 0.01
新しい学習率: 0.04
  • ウォームアップスケジュール
    • 最初は学習率を小さく設定し、一定エポックごとに学習率を増加させて安定化を図る。

実装例）

import matplotlib.pyplot as plt

# ウォームアップスケジュールを定義する関数
def warmup_schedule(total_epochs, base_lr, max_lr, warmup_epochs):
    """
    ウォームアップスケジュールを生成します。

    Parameters:
        total_epochs (int): 総エポック数
        base_lr (float): 初期学習率
        max_lr (float): 最大学習率
        warmup_epochs (int): ウォームアップ期間（エポック数）

    Returns:
        list: 各エポックの学習率
    """
    learning_rates = []
    for epoch in range(1, total_epochs + 1):
        if epoch <= warmup_epochs:
            # 線形増加
            lr = base_lr + (max_lr - base_lr) * (epoch / warmup_epochs)
        else:
            # ウォームアップ後は一定
            lr = max_lr
        learning_rates.append(lr)
    return learning_rates

# パラメータ設定
total_epochs = 20        # 総エポック数
base_lr = 0.001          # 初期学習率
max_lr = 0.01            # 最大学習率
warmup_epochs = 5        # ウォームアップ期間（エポック数）

# 学習率スケジュールの生成
learning_rates = warmup_schedule(total_epochs, base_lr, max_lr, warmup_epochs)

# 結果の表示
print("各エポックの学習率:")
for epoch, lr in enumerate(learning_rates, start=1):
    print(f"Epoch {epoch}: {lr:.6f}")

# 学習率スケジュールをプロット
plt.plot(range(1, total_epochs + 1), learning_rates, marker='o')
plt.title("Learning Rate Warmup Schedule")
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.grid()
plt.show()

結果の例）

各エポックの学習率:
Epoch 1: 0.002800
Epoch 2: 0.004600
Epoch 3: 0.006400
Epoch 4: 0.008200
Epoch 5: 0.010000
Epoch 6: 0.010000
バッチサイズが学習に与える影響
バッチサイズ特徴影響メリットデメリット
小バッチサイズ– 学習ノイズが多い
– 勾配が多様に変化		– 収束速度が遅くなる可能性
– モデルの一般化性能が向上		– 過学習を抑制- モデルの汎化性能向上
– メモリ効率が良い		– 学習が不安定になる場合がある
大バッチサイズ– 勾配の計算が正確
– 収束が安定		– 局所的最適解に陥りやすい
– 一般化性能が低下する場合がある		– 収束速度が速い
– 損失が滑らかに減少
– GPU効率が高い		– 過剰なメモリ使用
– 汎化性能が低下するリスク
ミニバッチ学習の実装例

今回は比較的大きなデータである、CIFAR-10データセットを使用してシンプルなCNN（畳み込みニューラルネットワーク）モデルをバッチ学習で実装します。

ライブラリのインポート

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader

シンプルなCNNモデルの定義

ここではまだ説明を行なっていませんが、CNNモデルを用いてモデルの定義を行います。CNNは次回のブログで詳細の説明を行います。

class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        self.conv1 = nn.Conv2d(3, 32, kernel_size=3, padding=1)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
        self.pool = nn.MaxPool2d(kernel_size=2, stride=2, padding=0)
        self.fc1 = nn.Linear(64 * 8 * 8, 512)
        self.fc2 = nn.Linear(512, 10)
        self.relu = nn.ReLU()
        self.dropout = nn.Dropout(0.5)
    
    def forward(self, x):
        x = self.pool(self.relu(self.conv1(x)))
        x = self.pool(self.relu(self.conv2(x)))
        x = x.view(-1, 64 * 8 * 8)
        x = self.relu(self.fc1(x))
        x = self.dropout(x)
        x = self.fc2(x)
        return x

データの前処理

transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
  • transforms.Compose
    • transforms.Composeは、複数の変換を順番に適用するためのコンテナです。この場合、2つの変換（transforms.ToTensor と transforms.Normalize）を順番に適用します。
  • transforms.ToTensor
    • transforms.ToTensorは、PIL画像またはNumPy配列をPyTorchのテンソルに変換します。つまり画像のピクセル値を [0, 255] の範囲から [0.0, 1.0] の範囲にスケーリングを行なっています。
  • transforms.Normalize
    • transforms.Normalizeは、テンソルの各チャンネル（RGB）を正規化します。この場合、各チャンネルの平均を 0.5、標準偏差を 0.5 として正規化します。

CIFAR-10データセットの読み込み

torchvision.datasets.CIFAR10を使用して、CIFAR-10データセットを読み込みます。DataLoaderを使用して、トレーニングデータとテストデータのバッチを作成します。

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = DataLoader(trainset, batch_size=64, shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = DataLoader(testset, batch_size=64, shuffle=False, num_workers=2)

デバイスの設定

GPUが利用可能な場合はGPUを使用し、そうでない場合はCPUを使用します。

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f'Using device: {device}')

モデル、損失関数、最適化アルゴリズムの初期化

シンプルなCNNモデルのインスタンスを作成し、損失関数と最適化アルゴリズムを設定します。

model = SimpleCNN().to(device)
criterion = nn.CrossEntropyLoss()  # クロスエントロピー損失
optimizer = optim.Adam(model.parameters(), lr=0.001)  # Adamオプティマイザ

ミニバッチ学習ループ

num_epochs = 10  # エポック数

for epoch in range(num_epochs):
    model.train()  # 訓練モード
    
　　# ミニバッチごとのトレーニングループ
    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        inputs, labels = data
        inputs, labels = inputs.to(device), labels.to(device)
        
        # 勾配をリセット
        optimizer.zero_grad()
        
        # 順伝播
        outputs = model(inputs)
        
        # 損失の計算
        loss = criterion(outputs, labels)
        
        # 勾配の計算とパラメータの更新
        loss.backward()
        optimizer.step()
        
        # 損失の累積
        running_loss += loss.item()
        if i % 100 == 99:    # 100ミニバッチごとにログを出力
            print(f'[Epoch {epoch + 1}, Batch {i + 1}] loss: {running_loss / 100:.3f}')
            running_loss = 0.0
    
    # テストデータでの評価
    model.eval()  # 評価モード
    correct = 0
    total = 0
    with torch.no_grad():
        for data in testloader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)
            outputs = model(images)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    
    print(f'Accuracy of the network on the 10000 test images: {100 * correct / total:.2f}%')

print('Finished Training')
トレーニング損失の減少
・各エポックごとにトレーニング損失が減少していることがわかります。
Using device: cpu
[Epoch 1, Batch 100] loss: 1.906
[Epoch 1, Batch 200] loss: 1.554
[Epoch 1, Batch 300] loss: 1.465

Accuracy of the network on the 10000 test images: 59.92%
[Epoch 2, Batch 100] loss: 1.110
[Epoch 2, Batch 200] loss: 1.082
[Epoch 2, Batch 300] loss: 1.080

テストデータの精度の向上
・各エポックの終わりにテストデータでの精度が計算され、精度が向上していることがわかります。
・モデルがトレーニングデータだけでなく、テストデータに対しても良い性能を示していることがわかります。
Accuracy of the network on the 10000 test images: 66.54%
[Epoch 3, Batch 100] loss: 0.912
[Epoch 3, Batch 200] loss: 0.895
[Epoch 3, Batch 300] loss: 0.931
  1. エポックごとのトレーニングループ:
    • 各エポックの開始時にモデルを訓練モードに設定します。
  2. ミニバッチごとのトレーニングループ:
    • trainloader からミニバッチを取得し、入力データとラベルに分け、デバイスに転送します。
    • 勾配をリセットし、順伝播、損失の計算、勾配の計算とパラメータの更新を行います。
    • 各ミニバッチの損失を累積し、100ミニバッチごとに平均損失をログに出力します。
  3. テストデータでの評価:
    • 各エポックの終わりにモデルを評価モードに設定し、テストデータでモデルを評価します。
    • torch.no_grad() ブロック内で勾配計算を無効にし、テストデータでモデルを評価します。
    • テストデータの予測値 outputs を計算し、正解数 correct と総数 total を累積します。
    • テストデータの精度を計算し、ログに出力します。
  4. トレーニングの終了:
    • トレーニングが終了したことをログに出力します。

GPU並列処理の活用術

GPU並列処理とバッチ学習は、効率的なモデルトレーニングにおいて密接に関連しています。バッチ学習はデータを一括で処理するため、行列演算が中心となります。この行列演算はGPUが得意とする大量の並列計算に最適化されており、計算速度を大幅に向上させます。また、大きなバッチサイズを選択することでGPUのリソースを最大限に活用でき、トレーニングの効率がさらに高まります。その結果、大規模データセットや複雑なモデルでも短時間での学習が可能になります。

GPU並列処理の仕組み

CPUとGPUの違い

  • CPU (Central Processing Unit)
    • 少数の強力なコアを持つ。
    • シリアルタスク（逐次処理）に優れる。

CPUの特徴

CPUは人間の脳で例えると「論理的な思考を行う部分」に相当します。少数の強力な「ニューロン」（コア）が存在し、複雑な計算や意思決定を順序立てて処理します。たとえば、難しい数学問題をじっくり解くような作業が得意です。計算処理では、逐次的なタスク（シングルスレッド処理）を素早く正確にこなします。ただし、同時に多くのタスクを処理する場合は限界があります。そのため、タスクが分散される並列処理には不向きです。

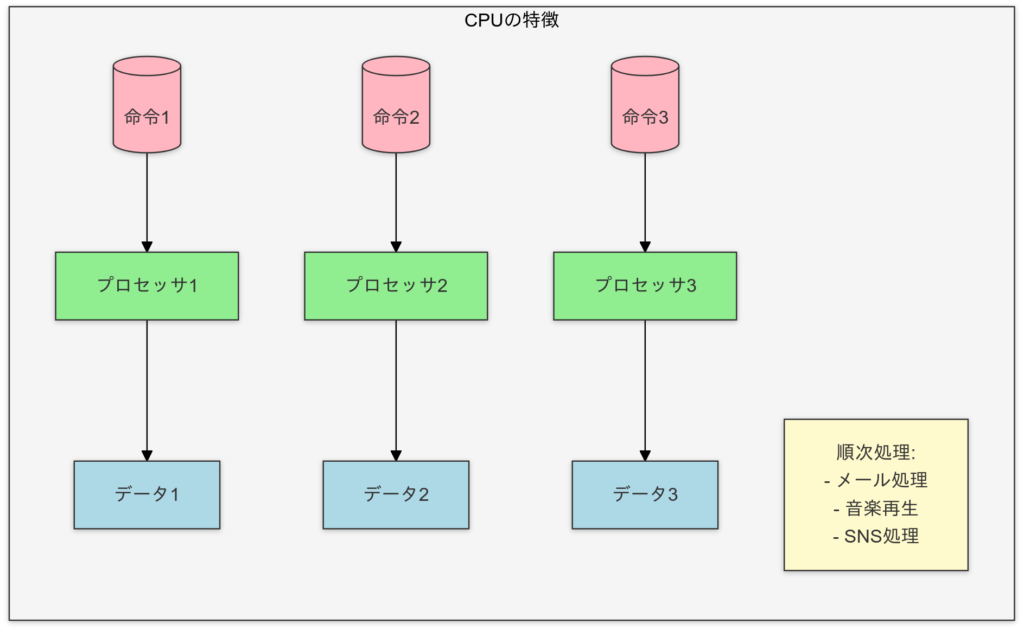
  • GPU(Graphics Processing Unit)
    • 数千のシンプルなコアを持つ。
    • 行列演算のようなデータ並列タスクに最適。

GPUの特徴

GPUは脳で例えると「視覚処理やパターン認識を行う部分」に相当します。多数の単純な「ニューロン」（コア）が並列に配置され、シンプルなタスクを一斉に処理します。計算処理では、行列演算や画像処理など、大量のデータを同時に計算する並列タスクが得意です。これは、人間が視覚情報を短時間で処理する働きに似ています。ただし、複雑で順序が必要な処理は苦手です。

GPUは、大量の数値演算を同時に実行できるため、ディープラーニングの行列演算（例: フォワード/バックプロパゲーション）において特に有利です。

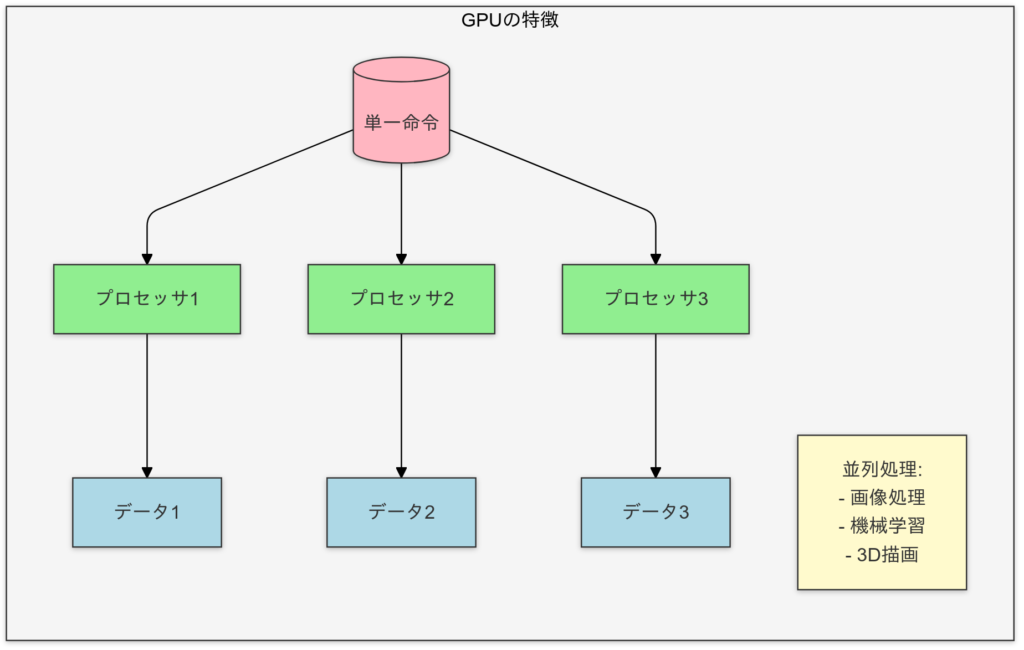
GPU並列処理の概要

  • データを小さな計算単位（スレッド）に分割し、それぞれを並列処理。
  • 高速なビデオメモリ（VRAM）にアクセスし、データ転送を効率化。
  • 行列の掛け算や畳み込み演算を専用のハードウェアで加速。

GPUを使うメリット

メリット詳細効果
高速化– 大規模データセットを短時間で処理可能- 複雑なモデル（例: トランスフォーマー）の学習時間を短縮– モデル学習の効率化
– 計算速度の向上
メモリ効率– VRAMを活用して大量データを保持可能- バッチサイズを増加させて学習効率を向上– メモリ制約を軽減- バッチ処理のスループット向上
柔軟性– モデルやデータをGPUに割り当てて並列実行可能– 複数のタスクを同時に実行
– ハードウェアの最大利用

GPUの有効化と設定

NVIDIA GPUの有効化と設定

NVIDIAのGPUはディープラーニングの主要な選択肢で、CUDA (Compute Unified Device Architecture) を利用します。CUDAはGPUを計算タスクに特化させたAPIとライブラリを提供します。

前提条件

  • 対応ハードウェア：NVIDIA製のGPU。
  • OS：Windows、Linux。
  • ソフトウェア：
    • NVIDIAドライバ
    • CUDA Toolkit
    • cuDNN (NVIDIAのディープラーニング向けライブラリ)

設定手順

  • NVIDIAドライバのインストール
    • NVIDIA公式サイト から、使用するGPUに対応する最新ドライバをダウンロードしてインストール。
  • CUDA Toolkitのインストール
    • CUDA Toolkit公式サイト から適切なバージョンをダウンロード。
    • ダウンロードしたファイルをCUDAインストールディレクトリに展開。
  • cuDNNのインストール
    • cuDNN公式サイト からCUDAバージョンに対応するcuDNNをダウンロード。
    • ダウンロードしたファイルをCUDAインストールディレクトリに展開。

PyTorchでの設定

import torch
print(torch.cuda.is_available())  # Trueなら有効

macの場合はこうなります。

GPUデバイスの使用

モデルやデータをGPUに転送して計算。GPUを使用するには、モデルとテンソル（データ）をGPUに移動する必要があります。

# デバイスの設定
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') 

# モデルをデバイスに転送
model = model.to(device)

# データをデバイスに転送
data = data.to(device)

pin_memory=True でデータ転送を高速化

pin_memory=True オプションを使用してデータの転送を高速化が可能です。以下はその例です。

# データローダーの作成
batch_size = 16
pin_memory = device.type == 'cuda'  # CUDAが利用可能な場合にのみpin_memory=Trueを設定
train_dataset = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True, pin_memory=pin_memory)

複数GPUの活用（データ並列化）

  • データ並列処理
    • 複数GPUを用いる場合、torch.nn.DataParallel または torch.nn.parallel.DistributedDataParallel を使用します。
      これにより、データを複数のGPUに分散して処理可能です。
# DataParallelを使用した例
model = nn.DataParallel(model)
model.to(device)

Apple Silicon GPUの有効化と設定

Apple Silicon (M1、M2) のGPUはMetal APIを活用し、Metal Performance Shaders (MPS) がPyTorch 1.12以降でサポートされています。

前提条件

  • 対応ハードウェア： M1、M2チップを搭載したMac。
  • OS：macOS Monterey 12.3以降。
  • ソフトウェア：
    • PyTorch 1.12以降
    • macOSに組み込まれたMetal API（別途インストール不要）

設定手順

  • PyTorchのインストール
    • Metalバックエンド対応のPyTorchをインストール。
pip install torch torchvision torchaudio

GPUデバイスの確認

  • Metalバックエンドが有効か確認。
import torch
print(torch.backends.mps.is_available())  # Trueなら有効

GPUデバイスの使用

  • Metal GPU (mps) を指定して計算。GPUを使用するには、モデルとテンソル（データ）をGPUに移動する必要があります。
# デバイスの設定
device = torch.device('mps' if torch.backends.mps.is_available() else 'cpu')

# モデルをデバイスに転送
model = model.to(device)

# データをデバイスに転送
data = data.to(device)

pin_memory=True でデータ転送を高速化

pin_memory=True オプションを使用してデータの転送を高速化が可能です。以下はその例です。

# データローダーの作成
batch_size = 16
train_dataset = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True, pin_memory=True)

注意点

  • 現在の所、Apple Silicon GPUでは複数GPUの活用は未対応でした。

Intel GPUの有効化と設定

Intel GPUは、OpenCLまたはoneAPIによって計算に利用できます。Intelは近年、oneAPIを推進しており、ディープラーニング向けライブラリとしてIntel Extension for PyTorchを提供しています。

前提条件

  • 対応ハードウェア：Intel製統合GPU（Iris Xeなど）。
  • OS：Windows、Linux。
  • ソフトウェア：
    • Intel oneAPI Base Toolkit
    • Intel Extension for PyTorch

設定手順

  • Intel oneAPI Base Toolkitのインストール
  • Intel Extension for PyTorchのインストール
    • oneAPI GPUで動作するPyTorch拡張をインストール。
pip install intel-extension-for-pytorch

PyTorchでの設定

  • Intel GPUを利用可能か確認します。GPUを使用するには、モデルとテンソル（データ）をGPUに移動する必要があります。
# デバイスの設定
device = torch.device('opencl' if torch.backends.opencl.is_available() else 'cpu')

# モデルをデバイスに転送
model = model.to(device)

# データをデバイスに転送
data = data.to(device)

最適化

  • Intel Extension for PyTorchを使用してモデルを最適化。
model = ipex.optimize(model)

それぞれのGPUの比較

GPUプラットフォームAPI / ライブラリ利点注意点
NVIDIACUDA, cuDNN高速・安定した性能、豊富なライブラリ対応GPUが必要、ドライバの管理が必要
Apple SiliconMetal, MPS統合メモリによる効率的なデータ転送一部未対応のPyTorch機能がある
InteloneAPI, OpenCL手軽に統合GPUが利用可能、oneAPIによる最適化性能はNVIDIAやAppleに劣る場合がある

Kaggle NotebookでのGPU有効化

  • Kaggle Notebookでは、GPUを有効にするために「Accelerator」を「GPU」に設定します。その後、torch.device('cuda') でデバイスを指定します。
GPU活用のベストプラクティス（Apple Silicon）
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from torch.utils.data import DataLoader, TensorDataset

# シンプルな非線形分類モデル（多層パーセプトロン）
class NeuralNetworkModel(nn.Module):
    def __init__(self, input_dim):
        super(NeuralNetworkModel, self).__init__()
        self.model = nn.Sequential(
            nn.Linear(input_dim, 64),    # 入力層から隠れ層1
            nn.ReLU(),                    # 活性化関数
            nn.Linear(64, 32),            # 隠れ層1から隠れ層2
            nn.ReLU(),                    # 活性化関数
            nn.Linear(32, 3)              # 隠れ層2から出力層（3クラス分類）
        )
    
    def forward(self, x):
        return self.model(x)

# データの読み込み
wine = load_wine()
X = wine.data
y = wine.target

# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# データの分割
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.2, random_state=42, stratify=y
)

# データをPyTorchのテンソルに変換
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.long)
y_test = torch.tensor(y_test, dtype=torch.long)

# デバイスの設定（Metalが利用可能ならMetalを使用）
device = torch.device('mps' if torch.backends.mps.is_available() else 'cpu')
print(f'Using device: {device}')

# モデルをデバイスに転送
model = NeuralNetworkModel(X_train.shape[1]).to(device)

# データをデバイスに転送
X_train = X_train.to(device)
y_train = y_train.to(device)
X_test = X_test.to(device)
y_test = y_test.to(device)

# モデル、損失関数、最適化アルゴリズムの初期化
criterion = nn.CrossEntropyLoss()  # クロスエントロピー損失
optimizer = optim.Adam(model.parameters(), lr=0.001)  # 学習率を0.001に設定

# データローダーの作成
batch_size = 16
train_dataset = TensorDataset(X_train, y_train)
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True, pin_memory=True)

# ミニバッチ学習ループ
num_epochs = 100  # エポック数

for epoch in range(num_epochs):
    model.train()  # 訓練モード
    
    for X_batch, y_batch in train_loader:
        X_batch, y_batch = X_batch.to(device), y_batch.to(device)
        
        # 勾配をリセット
        optimizer.zero_grad()
        
        # モデルの予測
        outputs = model(X_batch)
        
        # 損失の計算
        loss = criterion(outputs, y_batch)
        
        # 勾配の計算とパラメータの更新
        loss.backward()
        optimizer.step()
    
    # ログ出力と評価
    if (epoch + 1) % 10 == 0:  # 10エポックごとにログを出力
        model.eval()  # 評価モード
        with torch.no_grad():
            # 訓練データの予測
            train_outputs = model(X_train)
            _, train_preds = torch.max(train_outputs, 1)
            accuracy_train = (train_preds == y_train).sum().item() / y_train.size(0)
            
            # テストデータの予測
            test_outputs = model(X_test)
            _, test_preds = torch.max(test_outputs, 1)
            accuracy_test = (test_preds == y_test).sum().item() / y_test.size(0)
        
        print(f"Epoch {epoch + 1}: Loss = {loss.item():.4f}, "
              f"Accuracy (Train) = {accuracy_train:.4f}, "
              f"Accuracy (Test) = {accuracy_test:.4f}")

# 最終的なモデルのパラメータを出力
for name, param in model.named_parameters():
    print(f"{name}: {param.data}")

バッチ正規化 (Batch Normalization)

バッチ正規化 (Batch Normalization, BN) は、ディープラーニングにおいて学習を安定化し、収束速度を向上させる手法です。

バッチ正規化の背景と目的

ニューラルネットワークの学習時、各層の入力分布が変動する現象を「内部共変量シフト」と呼びます。この現象は、モデルの収束速度を低下させたり、勾配消失・爆発を引き起こす原因となります。

バッチ正規化の目的

バッチ正規化は、各バッチ内で入力特徴量を正規化することで、以下を実現します。

  • 各層の入力分布を一定に保つ。
  • 学習率を高く設定しても安定性を維持。
  • 勾配消失や爆発を防止。

バッチ正規化の処理ステップと数式

ミニバッチ内の平均と分散を計算

  • 入力特徴量 $x_i$ に対し、バッチ統計量を計算します。

$$\mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i, \quad \sigma_B^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i – \mu_B)^2$$

$m$：バッチサイズ。$x_i$​：バッチ内の $i$-番目のサンプル。

入力特徴量の正規化

バッチ内の特徴量を正規化して、平均0・分散1に調整します。

$$\hat{x}_i = \frac{x_i – \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$$

$ϵ$ は、分母がゼロになるのを防ぐための小さな定数です。

スケールとシフト

正規化された特徴量に学習可能なパラメータ $γ$（スケール）と $β$（シフト）を適用します。

$$y_i = \gamma \hat{x}_i + \beta$$

これにより、モデルが特徴量の分布を再調整可能になります。

バッチ正規化のメリット
メリット詳細
収束速度の向上学習率を高く設定可能になり、収束が速くなる。
勾配消失・爆発の緩和層間の勾配が安定し、深いネットワークでも学習が可能。
汎化性能の向上過学習の抑制効果も観察される。
バッチ正規化の図解

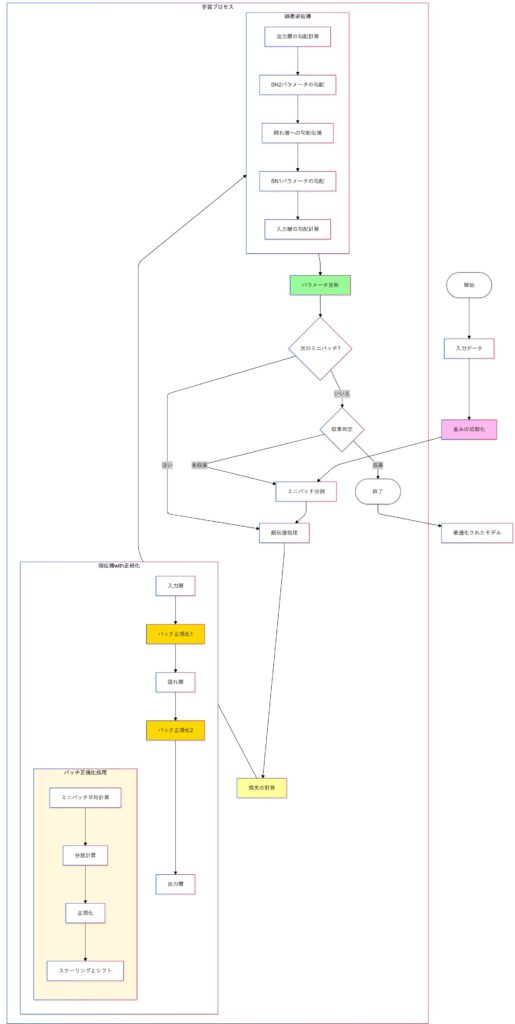
他の正規化手法との違い

バッチ正規化は、特にCNNにおいて広く使われる標準的な手法で、高速な収束と学習の安定性をもたらします。一方で、他の正規化手法には、それぞれ特定のタスクやモデル要件に適した特性があります。例えば、データの構造やバッチサイズの制約、モデルの設計に応じて適切な手法を選ぶことで、モデルの性能を最大限に引き出すことができます。そのため、使用する正規化手法を柔軟に選び分けることが、より効果的な学習を実現する鍵となります。

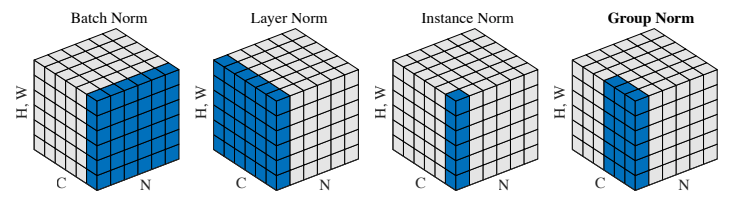
バッチ正規化
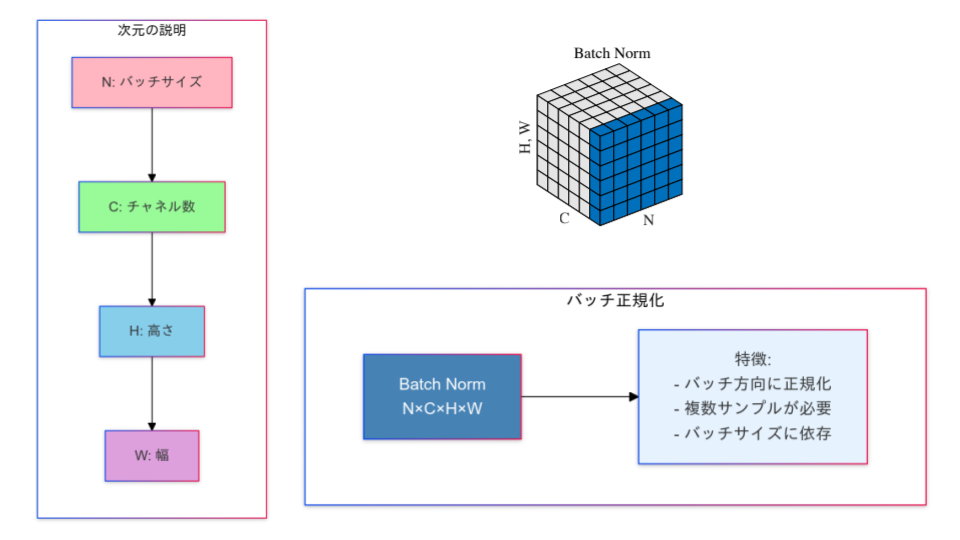
正規化手法正規化単位特徴適用例
バッチ正規化 (BN)バッチ全体の特徴ごと– バッチ内の統計を利用し、学習の安定性と収束速度を向上。
– 高い学習率を許容。
– バッチサイズに依存。		CNNや大規模データセットの学習。
正規化手法メリットデメリット
バッチ正規化 (BN)– 高い学習率を許容し、収束速度が速い。
– 深いネットワークでも勾配が安定。
– 過学習の抑制効果。		– バッチサイズが小さい場合、統計が不安定。
– トレーニングと推論で異なる統計を使用する複雑さ。

PyTorchによる正規化手法の実装例

import torch.nn as nn

# バッチ正規化層
bn_layer = nn.BatchNorm2d(32)  # 入力チャネル数を指定 (例: 32)
レイヤー正規化
正規化手法正規化単位特徴適用例
レイヤー正規化 (LN)各サンプルの層全体の特徴量– 各サンプルを独立に正規化。
– バッチサイズに依存しないため、小さなバッチサイズやシーケンシャルデータに適合。		NLPや時系列データ（RNN, Transformer）。
正規化手法メリットデメリット
レイヤー正規化 (LN)– バッチサイズに依存せず、小さなバッチサイズでの学習が可能。
– シーケンシャルデータやNLPに適合。		– CNNのような空間的な特徴を扱うタスクでは効果が限定的。

PyTorchによる正規化手法の実装例

# レイヤー正規化層
ln_layer = nn.LayerNorm([64, 64])  # 入力特徴量の形状 (例: 64x64)
インスタンス正規化
正規化手法正規化単位特徴適用例
インスタンス正規化 (IN)各サンプルのチャネルごと– 各サンプルのチャネルを独立に正規化。
– バッチ間の依存なし。
– 特にスタイル転移や画像生成タスクに適合。		画像生成やスタイル変換。
正規化手法メリットデメリット
インスタンス正規化 (IN)– 各サンプルを独立に正規化するため、スタイル転移や画像生成タスクに効果的。– 汎化性能が他の手法に劣る場合がある。
– バッチ間の特徴共有がないため、大規模データでの性能は限定的。

PyTorchによる正規化手法の実装例

# インスタンス正規化層
in_layer = nn.InstanceNorm2d(32)  # 入力チャネル数を指定 (例: 32)
グループ正規化
正規化手法正規化単位特徴適用例
グループ正規化 (GN)チャネルをいくつかのグループに分割– バッチサイズに依存せず、チャネルをグループ単位で正規化。
– 小バッチ環境や3D CNNで有用。		小バッチサイズや3Dデータの学習。
正規化手法メリットデメリット
グループ正規化 (GN)– 小バッチサイズや3Dデータで安定性を提供。
– バッチサイズに依存せず、CNNで高い性能を発揮。		– グループ数やチャネル数の選択に敏感で、モデル設計時に調整が必要。

PyTorchによる正規化手法の実装例

# グループ正規化層
gn_layer = nn.GroupNorm(num_groups=8, num_channels=32)  # グループ数とチャネル数を指定

最適化アルゴリズムの選択と活用

最適化アルゴリズムとは？

最適化アルゴリズムは、誤差逆伝播法（バックプロパゲーション）と連動して機械学習モデルの学習を支えています。この仕組みは、脳のニューロンがシナプスを通じて信号を伝達し、その強度を経験に基づいて調整するプロセスを模倣しています。誤差逆伝播法では、損失関数の勾配を計算し、その情報を最適化アルゴリズム（例: 勾配降下法やAdam）に渡してパラメータを更新します。ニューロンの学習のように、この反復的な更新によりモデルはデータのパターンを効率的に学習し、精度を高めていきます。この結びつきにより、誤差の伝達と最適化が一体となって機械学習の効果を発揮しています。

【第9回】ディープラーニングの基礎とCNNの仕組み（前編)
目的 このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用...
shion.blog
2024.11.23

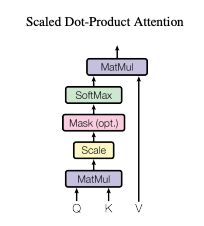
最適化アルゴリズムの紹介（最急降下法・SGD）

【第6回】線形回帰とロジスティック回帰の実装と最急降下法の役割で最適化アルゴリズムを紹介しましたが、今回はKaggleなどの実践的なデータサイエンスやディープラーニングのタスクで活用される最適化アルゴリズムを紹介してみようと思います。最急降下法やSGDについては【第6回】のブログを参照して下さい。

最急降下法：

https://shion.blog/the-6th-machine-learning-workshop/#toc8

SGD：

【第6回】線形回帰とロジスティック回帰の実装と最急降下法の役割
目的 このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用...
shion.blog
2024.10.29

Momentum

Momentumは、勾配降下法の収束速度を向上させるために考案されたアルゴリズムで、過去の勾配を考慮に入れながらパラメータ更新を行います。これにより、振動を抑えつつ効率的に収束することが可能になります。

更新式：

  • モーメントの計算：

$$v_t = \beta v_{t-1} + (1 – \beta) g_t$$

  • $v_t$： 時刻 $t$ のモーメント（速度）。
  • $g_t​$： 現在の勾配。
  • $β$： モーメントの減衰率（通常 $\beta = 0.9$）。

パラメータの更新：

$$w_{t+1} = w_t – \alpha v_t$$

  • $w_t$​： 時刻 $t$ のパラメータ。
  • $α$: 学習率。

特徴：

項目内容
速度（モーメント）の利用過去の勾配方向を蓄積して「慣性」を持たせ、更新方向をスムーズに調整。局所的な振動（例: 谷間での左右の揺れ）を抑制。
効率的な収束勾配が一貫した方向に向いている場合、モーメントによる加速効果で収束速度が向上。
スケーラブル簡単に計算可能で、さまざまなタスクに適用できる。

利点：

項目内容
振動の抑制勾配が急峻な谷の周辺（特に縦に急で横に緩い場合）での振動を低減。
収束の加速勾配が一貫して変化する場合、より高速に収束。

欠点：

項目内容
局所最適解の探索が難しい慣性が働きすぎると、細かい最適解を逃す可能性がある。
学習率の調整が必要モーメント係数（β）や学習率（α）の適切な設定が必要。

適用例：

  • 単純な勾配降下法が振動する場合：
    • 非対称なコスト関数（例: 長く狭い谷）において、収束速度を向上。
  • CNNや一般的なMLPモデル：
    • 深層学習モデルのトレーニングで広く使用。

動作イメージ

Momentumは、物理学の慣性運動を模倣しています。現在の勾配だけでなく、過去の勾配も考慮することで、最適解に向かってスムーズに進むよう設計されています。山や谷の形状に応じて加速や減速を調整しながら、効率的に最適化します。

import numpy as np
import matplotlib.pyplot as plt

def func(x, y):
    """二次関数（楕円形状）の定義"""
    return 0.1 * x**2 + y**2

def grad_func(x, y):
    """関数の勾配を計算"""
    grad_x = 0.2 * x
    grad_y = 2 * y
    return np.array([grad_x, grad_y])

def momentum_optimization(x_init, y_init, learning_rate=0.1, momentum=0.9, steps=50):
    """モメンタム最適化の実行"""
    x, y = x_init, y_init
    v = np.array([0.0, 0.0])
    trajectory = [(x, y)]
    velocity_history = [v.copy()]
    
    for _ in range(steps):
        grad = grad_func(x, y)
        v = momentum * v - learning_rate * grad  # モメンタム更新式
        x, y = x + v[0], y + v[1]
        trajectory.append((x, y))
        velocity_history.append(v.copy())
    
    return np.array(trajectory), np.array(velocity_history)

def plot_contour_with_trajectory(func, trajectory, velocity_history, levels=20):
    """等高線と最適化の軌跡をプロット"""
    x_range = np.linspace(-10, 10, 400)
    y_range = np.linspace(-10, 10, 400)
    X, Y = np.meshgrid(x_range, y_range)
    Z = func(X, Y)
    
    plt.figure(figsize=(10, 8))
    contour = plt.contour(X, Y, Z, levels=levels, cmap="cool")
    plt.clabel(contour, inline=True, fontsize=8)
    
    # 軌跡のプロット
    plt.plot(trajectory[:, 0], trajectory[:, 1], 'ro-', markersize=5, label="Momentum Path")
    
    # 初期点と最終点のマーカー
    plt.scatter(trajectory[0, 0], trajectory[0, 1], color='green', s=100, label='Start')
    plt.scatter(trajectory[-1, 0], trajectory[-1, 1], color='blue', s=100, label='End')
    
    # 矢印を追加して速度ベクトルを示す（間引いて表示）
    for i in range(0, len(trajectory), 5):
        plt.arrow(trajectory[i, 0], trajectory[i, 1],
                  velocity_history[i, 0], velocity_history[i, 1],
                  head_width=0.3, head_length=0.3, fc='k', ec='k')
    
    plt.title("Momentum Optimization Trajectory")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.grid(True)
    plt.show()

# パラメータの設定
learning_rate = 0.1
momentum = 0.9
steps = 50
x_init, y_init = -8.0, 4.0

# 最適化の実行
trajectory, velocity_history = momentum_optimization(x_init, y_init, learning_rate, momentum, steps)

# プロットの作成
plot_contour_with_trajectory(func, trajectory, velocity_history)

モメンタムのコーディング例（PyTorch）

モメンタムはPyTorchのtorch.optim.SGD（確率的勾配降下法）オプティマイザに対する設定として使用できます。モメンタムを利用することで、勾配の過去の情報を考慮に入れたパラメータの更新が可能となり、最適化の収束速度を向上させたり、局所的な振動を抑えたりする効果があります。

import torch.optim as optim

# モメンタム付きSGDオプティマイザの設定
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

AdaGrad

AdaGrad は、学習率を各パラメータに適応させる最適化アルゴリズムで、過去の勾配の履歴を利用してパラメータごとの学習率を動的に調整します。この手法は、スパースなデータや特徴量に基づくタスク（例: 自然言語処理）で特に効果的です。

更新式：

  • 勾配の累積平方和の計算：

$$r_t = r_{t-1} + g_t^2$$

  • $r_t$​：時刻 $t$ における累積勾配の平方和。
  • $g_t$​：現在の勾配。

パラメータの更新：

$$w_{t+1} = w_t – \frac{\alpha}{\sqrt{{r_t} + \epsilon}} g_t$$

  • $\epsilon$： ゼロ割りを防ぐための小さな値（通常 $10^{-8}$）。

特徴：

項目内容
パラメータごとの適応学習率過去の勾配の累積に基づき、各パラメータに個別の学習率を割り当て。頻繁に更新されるパラメータは学習率が減少し、スパースなパラメータは学習率が維持される。
スパースなデータへの適応性自然言語処理やスパースなデータが多い状況で優れた性能を発揮。

利点：

項目内容
スパースデータでの有効性更新頻度の少ないパラメータに大きな学習率を適用するため、スパースなデータセットに適している。
簡単な計算累積平方和と勾配の更新だけで動作するため、計算コストが低い。

欠点：

項目内容
学習率の極端な減少勾配の累積平方和が増加し、学習率が極端に小さくなることでモデルの収束が遅くなる可能性がある。
適応力の制限長期間の学習で更新が進まなくなる「停滞問題」が発生することがある。

適用例

  • 自然言語処理
    • 単語埋め込み（word embedding）やテキスト分類など、スパースな特徴量を持つタスク。
  • スパースデータのトレーニング
    • 行列分解、協調フィルタリング、レコメンデーションシステムなど。

動作イメージ

AdaGradは、学習の初期段階で大きな学習率を適用してパラメータを大まかに調整し、学習が進むにつれて頻繁に更新されるパラメータには小さな学習率を適用して微調整を行います。この仕組みにより、スパースな特徴を持つタスクでも、あまり更新されないパラメータが学習から取り残されるのを防ぎます。

import numpy as np
import matplotlib.pyplot as plt

def func(x, y):
    """二次関数（楕円形状）の定義"""
    return 0.1 * x**2 + y**2

def grad_func(x, y):
    """関数の勾配を計算"""
    grad_x = 0.2 * x
    grad_y = 2 * y
    return np.array([grad_x, grad_y])

def adagrad_optimization(x_init, y_init, learning_rate=0.1, epsilon=1e-8, steps=50):
    """AdaGrad最適化の実行"""
    x, y = x_init, y_init
    G = np.array([0.0, 0.0])  # 勾配の累積二乗和
    trajectory = [(x, y)]
    update_history = []
    
    for t in range(1, steps + 1):
        grad = grad_func(x, y)
        
        # 勾配の累積二乗和の更新
        G += grad ** 2
        
        # パラメータの更新
        adjusted_lr = learning_rate / (np.sqrt(G) + epsilon)
        update = adjusted_lr * grad
        x = x - update[0]
        y = y - update[1]
        
        # 経路と更新量の記録
        trajectory.append((x, y))
        update_history.append(update.copy())
        
    return np.array(trajectory), np.array(update_history)

def plot_contour_with_trajectory(func, trajectory, update_history, levels=20):
    """等高線と最適化の軌跡をプロット"""
    x_range = np.linspace(-10, 10, 400)
    y_range = np.linspace(-10, 10, 400)
    X, Y = np.meshgrid(x_range, y_range)
    Z = func(X, Y)
    
    plt.figure(figsize=(10, 8))
    contour = plt.contour(X, Y, Z, levels=levels, cmap="cool")
    plt.clabel(contour, inline=True, fontsize=8)
    
    # 軌跡のプロット
    plt.plot(trajectory[:, 0], trajectory[:, 1], 'mo-', markersize=5, label="AdaGrad Path")
    
    # 初期点と最終点のマーカー
    plt.scatter(trajectory[0, 0], trajectory[0, 1], color='green', s=100, label='Start')
    plt.scatter(trajectory[-1, 0], trajectory[-1, 1], color='blue', s=100, label='End')
    
    # 矢印を追加して更新ベクトルを示す（間引いて表示）
    for i in range(0, len(trajectory) - 1, 5):
        plt.arrow(trajectory[i, 0], trajectory[i, 1],
                  update_history[i, 0], update_history[i, 1],
                  head_width=0.3, head_length=0.3, fc='k', ec='k')
    
    plt.title("AdaGrad Optimization Trajectory")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.grid(True)
    plt.show()

# パラメータの設定
learning_rate = 1.0  # AdaGradでは比較的大きな学習率が使用されることが多い
epsilon = 1e-8
steps = 50
x_init, y_init = -8.0, 4.0

# 最適化の実行
trajectory, update_history = adagrad_optimization(
    x_init, y_init,
    learning_rate=learning_rate,
    epsilon=epsilon,
    steps=steps
)

# プロットの作成
plot_contour_with_trajectory(func, trajectory, update_history)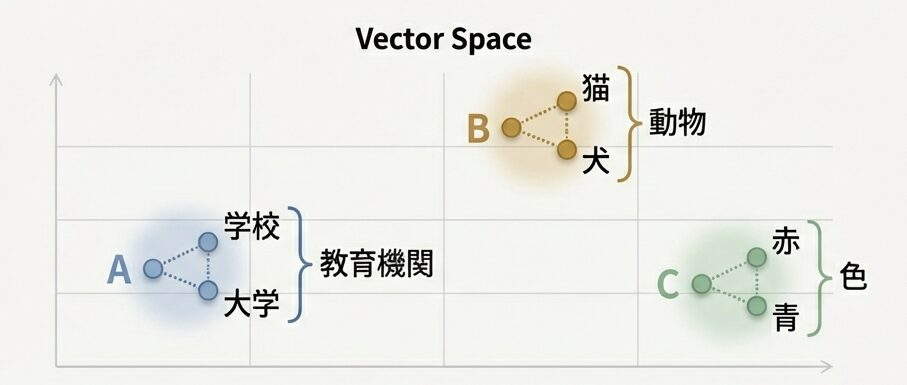

AdaGradのコーディング例（PyTorch）

import torch.optim as optim

# AdaGradオプティマイザの設定
optimizer = optim.Adagrad(model.parameters(), lr=0.01, lr_decay=0, weight_decay=0, eps=1e-10)

RMSprop

RMSprop は、AdaGradの改良版として提案された最適化アルゴリズムで、勾配の累積平方和が時間とともに増大し、学習率が極端に減少する問題を解決します。この手法は、オンライン学習やリカレントニューラルネットワーク（RNN）のトレーニングで特に効果的です。

更新式：

  • 指数移動平均による勾配の二乗の累積：

$$r_t = \beta r_{t-1} + (1 – \beta) g_t^2$$

  • $r_t$​：時刻 $t$ における勾配の二乗の移動平均。
  • $β$： 減衰率（通常 0.9）。
  • パラメータの更新

$$w_{t+1} = w_t – \frac{\alpha}{\sqrt{r_t} + \epsilon} g_t$$

特徴：

項目内容
移動平均の利用勾配の二乗の累積に指数移動平均を採用し、学習率の極端な減少を防止。古い勾配の影響を徐々に減少させる。
適応学習率勾配の大きさに基づいて各パラメータの学習率を調整。勾配が大きい場合は学習率を減少させ、小さい場合は学習率を増加。

利点：

項目内容
安定した学習勾配の変動が激しい場合でも安定した更新を提供。
長期学習への対応AdaGradで発生する学習率の極端な減少を解決し、長期間の学習でも効果を維持。
スパースデータへの有効性スパースな特徴量を持つタスクでも効果的に対応可能。

欠点：

項目内容
ハイパーパラメータ調整の必要性減衰率 $β$ や学習率 $α$ の適切な設定が重要で、パフォーマンスに大きく影響する。
局所最適解の探索が難しい学習率が小さくなりすぎる場合、収束が遅くなり、局所最適解の探索が困難になることがある。

適用例：

  • リカレントニューラルネットワーク (RNN)
    • 時系列データや自然言語処理での学習。
  • オンライン学習
    • ストリーミングデータや継続的なデータ処理。

動作イメージ

RMSpropは、勾配の変動が大きい場合でも安定した学習を可能にします。勾配の移動平均を利用して各パラメータの学習率を調整するため、スパースデータや連続データを扱うタスクで特に効果を発揮します。

import numpy as np
import matplotlib.pyplot as plt

def func(x, y):
    """二次関数（楕円形状）の定義"""
    return 0.1 * x**2 + y**2

def grad_func(x, y):
    """関数の勾配を計算"""
    grad_x = 0.2 * x
    grad_y = 2 * y
    return np.array([grad_x, grad_y])

def rmsprop_optimization(x_init, y_init, learning_rate=0.1, beta=0.9, epsilon=1e-8, steps=100):
    """RMSprop最適化の実行"""
    x, y = x_init, y_init
    Eg = np.array([0.0, 0.0])  # 勾配の二乗の移動平均
    trajectory = [(x, y)]
    update_history = []
    
    for t in range(1, steps + 1):
        grad = grad_func(x, y)
        
        # 勾配の二乗の移動平均を更新
        Eg = beta * Eg + (1 - beta) * grad ** 2
        
        # パラメータの更新
        update = (learning_rate / (np.sqrt(Eg) + epsilon)) * grad
        x = x - update[0]
        y = y - update[1]
        
        # 経路と更新量の記録
        trajectory.append((x, y))
        update_history.append(update.copy())
        
    return np.array(trajectory), np.array(update_history)

def plot_contour_with_trajectory(func, trajectory, update_history, levels=20):
    """等高線と最適化の軌跡をプロット"""
    x_range = np.linspace(-10, 10, 400)
    y_range = np.linspace(-10, 10, 400)
    X, Y = np.meshgrid(x_range, y_range)
    Z = func(X, Y)
    
    plt.figure(figsize=(10, 8))
    contour = plt.contour(X, Y, Z, levels=levels, cmap="cool")
    plt.clabel(contour, inline=True, fontsize=8)
    
    # 軌跡のプロット
    plt.plot(trajectory[:, 0], trajectory[:, 1], 'co-', markersize=3, label="RMSprop Path")
    
    # 初期点と最終点のマーカー
    plt.scatter(trajectory[0, 0], trajectory[0, 1], color='green', s=100, label='Start')
    plt.scatter(trajectory[-1, 0], trajectory[-1, 1], color='blue', s=100, label='End')
    
    # 矢印を追加して更新ベクトルを示す（間引いて表示）
    for i in range(0, len(trajectory) - 1, 10):
        plt.arrow(trajectory[i, 0], trajectory[i, 1],
                  update_history[i, 0], update_history[i, 1],
                  head_width=0.3, head_length=0.3, fc='k', ec='k')
    
    plt.title("RMSprop Optimization Trajectory")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.grid(True)
    plt.show()

# パラメータの設定
learning_rate = 0.1  # 学習率を0.1に増加
beta = 0.9
epsilon = 1e-8
steps = 100  # ステップ数を100に増加
x_init, y_init = -8.0, 4.0

# 最適化の実行
trajectory, update_history = rmsprop_optimization(
    x_init, y_init,
    learning_rate=learning_rate,
    beta=beta,
    epsilon=epsilon,
    steps=steps
)

# プロットの作成
plot_contour_with_trajectory(func, trajectory, update_history)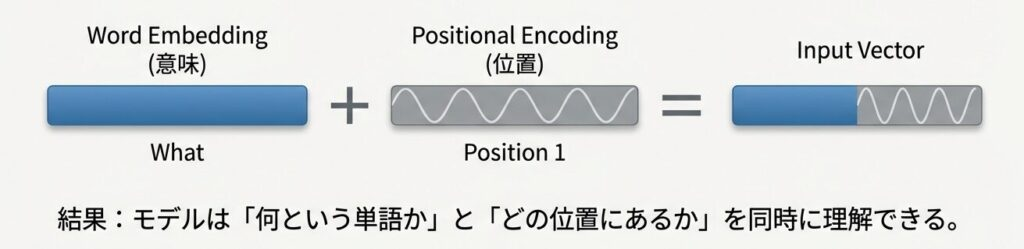

RMSpropのコーディング例（PyTorch）

import torch.optim as optim

# RMSpropオプティマイザの設定
optimizer = optim.RMSprop(model.parameters(), lr=0.001, alpha=0.9, eps=1e-8, weight_decay=0, momentum=0)

Adam

Adamは、勾配降下法を拡張したアルゴリズムで、学習率を各パラメータごとに調整します。過去の勾配を考慮し、勾配の一次モーメント（平均）と二次モーメント（分散）を利用します。

一次モーメントの更新式：

$$m_t = \beta_1 m_{t-1} + (1 – \beta_1) g_t$$

バイアス補正された一次モーメント：

$$\hat{m}_t = \frac{m_t}{1 – \beta_1^t}$$

二次モーメントの推定値：

$$v_t = \beta_2 v_{t-1} + (1 – \beta_2) g_t^2$$

バイアス補正を考慮した推定値：

$$\hat{v}_t = \frac{v_t}{1 – \beta_2^t}$$

重みの更新式

$$w_{t+1} = w_t – \alpha \frac{\hat{m}}{\sqrt{\hat{v} + \epsilon}}$$

特徴表記説明
勾配の一次モーメント$m_t$勾配の一次モーメント
勾配の二次モーメント$v_t$勾配の二次モーメント
現在の勾配$g_t$現在の勾配
モーメントの減衰率$\beta_1, \beta_2$モーメントの減衰率（通常 ($\beta_1 = 0.9,$ $\beta_2 = 0.999$)）
ゼロ割りを防ぐための小さな値$\epsilon$ゼロ割りを防ぐための小さな値（通常 ($1 \times 10^{-8})$）

このようにして、Adam最適化アルゴリズムでは、勾配の一次および二次モーメントを更新し、バイアス補正を行うことで、各パラメータに対する適応的な学習率を計算します。これにより、学習の安定性と効率が向上します。

利点：

特徴内容
自動的な学習率調整各パラメータに対する学習率を適応的に調整するため、収束が速く、安定性が向上します。
効果的な収束Adamは多くのデータセットで良い結果を得やすく、特に非定常な目的関数に対して効果的です。

適用例：

  • 幅広いディープラーニングタスク（例: CNN、RNN、NLP）での標準的な選択肢。
  • 画像認識、時系列データ処理、自然言語処理タスク（NLP）など汎用的。

動作イメージ

  • Adamでは、等高線プロット上で滑らかに最小値へ収束する経路が観察されます。各ステップの更新量は矢印で示され、パラメータの移動方向と大きさが視覚的に理解できます。一次および二次モーメントを利用し、各パラメータごとに適応的な学習率を調整することで、安定した収束が期待できます。
  • 平均的な道を進む車の運転。道路の凹凸や急カーブがあっても、ある程度一定の速度で進む。
import numpy as np
import matplotlib.pyplot as plt

def func(x, y):
    """二次関数（楕円形状）の定義"""
    return 0.1 * x**2 + y**2

def grad_func(x, y):
    """関数の勾配を計算"""
    grad_x = 0.2 * x
    grad_y = 2 * y
    return np.array([grad_x, grad_y])

def adam_optimization(x_init, y_init, learning_rate=0.1, beta1=0.9, beta2=0.999, epsilon=1e-8, steps=50):
    """Adam最適化の実行"""
    x, y = x_init, y_init
    m = np.array([0.0, 0.0])  # 一階モーメント (First Moment)
    v = np.array([0.0, 0.0])  # 二階モーメント (Second Moment)
    trajectory = [(x, y)]
    update_history = []
    
    for t in range(1, steps + 1):
        grad = grad_func(x, y)
        
        # モーメントの更新
        m = beta1 * m + (1 - beta1) * grad
        v = beta2 * v + (1 - beta2) * (grad ** 2)
        
        # バイアス補正
        m_hat = m / (1 - beta1 ** t)
        v_hat = v / (1 - beta2 ** t)
        
        # パラメータの更新
        update = learning_rate * m_hat / (np.sqrt(v_hat) + epsilon)
        x = x - update[0]
        y = y - update[1]
        
        # 軌跡と更新量の記録
        trajectory.append((x, y))
        update_history.append(update.copy())
    
    return np.array(trajectory), np.array(update_history)

def plot_contour_with_trajectory(func, trajectory, update_history, levels=20):
    """等高線と最適化の軌跡をプロット"""
    x_range = np.linspace(-10, 10, 400)
    y_range = np.linspace(-10, 10, 400)
    X, Y = np.meshgrid(x_range, y_range)
    Z = func(X, Y)
    
    plt.figure(figsize=(10, 8))
    contour = plt.contour(X, Y, Z, levels=levels, cmap="cool")
    plt.clabel(contour, inline=True, fontsize=8)
    
    # 軌跡のプロット
    plt.plot(trajectory[:, 0], trajectory[:, 1], 'mo-', markersize=5, label="Adam Path")
    
    # 初期点と最終点のマーカー
    plt.scatter(trajectory[0, 0], trajectory[0, 1], color='green', s=100, label='Start')
    plt.scatter(trajectory[-1, 0], trajectory[-1, 1], color='blue', s=100, label='End')
    
    # 矢印を追加して更新ベクトルを示す（間引いて表示）
    for i in range(0, len(trajectory) - 1, 5):
        plt.arrow(trajectory[i, 0], trajectory[i, 1],
                  update_history[i, 0], update_history[i, 1],
                  head_width=0.3, head_length=0.3, fc='k', ec='k')
    
    plt.title("Adam Optimization Trajectory")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.grid(True)
    plt.show()

# パラメータの設定
learning_rate = 0.1
beta1 = 0.9
beta2 = 0.999
epsilon = 1e-8
steps = 50
x_init, y_init = -8.0, 4.0

# 最適化の実行
trajectory, update_history = adam_optimization(
    x_init, y_init,
    learning_rate=learning_rate,
    beta1=beta1,
    beta2=beta2,
    epsilon=epsilon,
    steps=steps
)

# プロットの作成
plot_contour_with_trajectory(func, trajectory, update_history)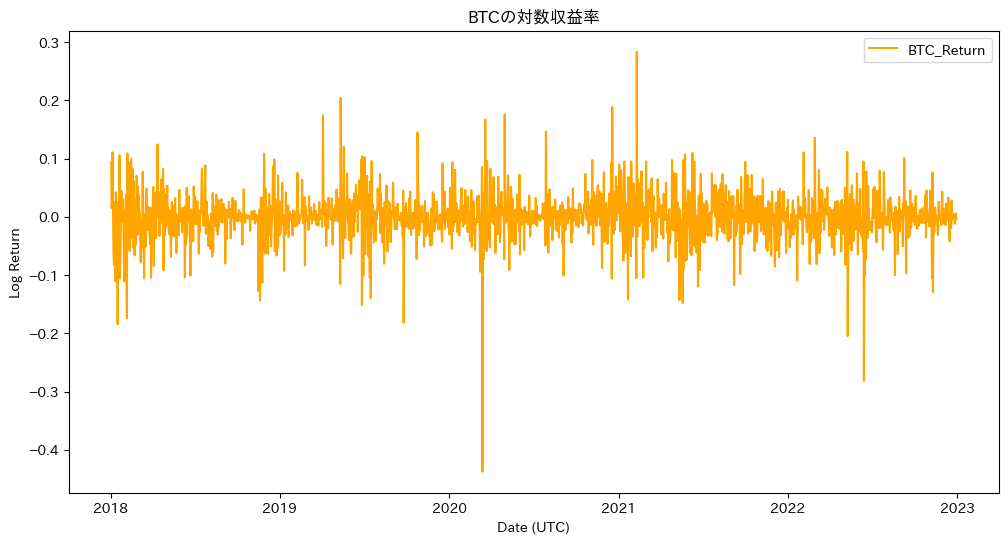

Adamのコーディング例（PyTorch）：

import torch.optim as optim

# Adamオプティマイザの設定
optimizer = optim.Adam(model.parameters(), lr=0.01)

AdamW

AdamW は、Adam最適化アルゴリズムの改良版であり、重み減衰 (Weight Decay) を正則化の手法として適切に導入したものです。重み減衰を「勾配更新」と独立して扱うことで、過学習を防ぎつつ、Adamの性能を保持しています。

Adamの元々の重み減衰問題：

  • 標準的なAdamでは、重み減衰を「L2正則化」として導入しますが、モーメントのスケーリングに影響されるため、理想的な正則化効果が得られない場合がありました。

解決策：

  • AdamWでは、重み減衰を勾配のモーメント計算に組み込まず、「パラメータ更新のステップ」において別途適用することで、この問題を解消しました。

アルゴリズムの詳細

  • 勾配のモーメント計算
    • Adamと同様に、一次モーメントと二次モーメントを計算します。

$$m_t = \beta_1 m_{t-1} + (1 – \beta_1) g_t$$

$$v_t = \beta_2 v_{t-1} + (1 – \beta_2) g_t^2$$

  • バイアス補正
    • モーメントのバイアス補正を行います。

$$\hat{m}_t = \frac{m_t}{1 – \beta_1^t}$$

$$\hat{v}_t = \frac{v_t}{1 – \beta_2^t}$$

  • 重み減衰 (Weight Decay)
    • AdamWでは、重み減衰をモーメント計算に含めず、更新式に直接加えます。

$$w_{t+1} = w_t – \alpha \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} – \eta \cdot \lambda \cdot w_t$$

特徴：

項目内容
重み減衰の分離正則化項を勾配計算と分離することで、理想的な正則化効果を実現。
汎化性能の向上過学習を抑制し、モデルの汎化性能を向上させます。
計算コストはAdamとほぼ同じ重み減衰の計算は単純なスケーリングであり、追加の計算コストがほとんど発生しません。

欠点：

  • 学習率と重み減衰係数の調整が必要
    • タスクに応じて適切な値を設定しないと、性能が十分に発揮されない可能性がある。

適用例：

  • Transformerベースのモデル
    • BERTやGPTなどの自然言語処理（NLP）の大規模モデル。
  • 画像認識タスク
    • CNNを用いた分類やセグメンテーションタスク。
  • 一般的なディープラーニングタスク
    • 汎化性能が重要な場合に有効。

論文：

Decoupled Weight Decay Regularization
L$_2$ regularization and weight decay regularization are equivalent for standard stochastic gradient descent (when resca...
arxiv.org
  • 従来のL2正則化では難しかった「学習率」と「重み減衰係数」を独立して調整できる手法として、分離型重み減衰を提案しました。この手法により、特にAdamのような適応型最適化手法でパフォーマンスが大幅に向上します。
  • 画像分類タスク（CIFAR-10やImageNet32x32）で、AdamWは従来のAdamより高いテスト精度を達成し、SGDとも互角に競える結果を示しました。特に、コサインアニーリングを併用することで汎化性能がさらに強化されました。
  • 提案された分離型重み減衰手法は、AdaGradやAMSGradなどの他の適応型最適化手法にも適用可能です。

動作イメージ

  • AdamWの動作イメージは、勾配更新（学習）と重み減衰（正則化）を分離して適用する点にあります。この設計により、パラメータが過剰に増大することを防ぎつつ、正確な学習を可能にします。
  • AdamWの役割
    • 勾配更新は「目的地に向かう最短ルートを計算する」作業。
    • 重み減衰は「荷物の重さを減らして動きやすくする」役割。
    • 両者を独立して処理することで、効率的かつ安定した移動が可能になります。
import numpy as np
import matplotlib.pyplot as plt
import torch

# 損失関数（例：楕円形）
def loss_function(x, y):
    return 0.1 * x**2 + y**2

# 損失関数の勾配
def gradient(x, y):
    return np.array([0.2 * x, 2 * y])

# AdamWのパラメータ更新関数
def adamw_update(x, y, m, v, m_hat, v_hat, grad, t, learning_rate, beta1, beta2, epsilon, weight_decay):
    m = beta1 * m + (1 - beta1) * grad
    v = beta2 * v + (1 - beta2) * (grad ** 2)

    m_hat = m / (1 - beta1 ** t)
    v_hat = v / (1 - beta2 ** t)

    x -= learning_rate * (m_hat[0] / (np.sqrt(v_hat[0]) + epsilon) + weight_decay * x)
    y -= learning_rate * (m_hat[1] / (np.sqrt(v_hat[1]) + epsilon) + weight_decay * y)

    return x, y, m, v, m_hat, v_hat

# パラメータ
x_start = -8
y_start = 9
learning_rate = 0.5  # 学習率
beta1 = 0.9  # 一次モーメントの減衰率
beta2 = 0.999  # 二次モーメントの減衰率
epsilon = 1e-8  # ゼロ除算を防ぐための小さな値
weight_decay = 0.1  # 重み減衰

# 初期位置
x = x_start
y = y_start

# モーメントの初期化
m = np.array([0.0, 0.0])
v = np.array([0.0, 0.0])
m_hat = np.array([0.0, 0.0])
v_hat = np.array([0.0, 0.0])

# 軌跡を保存するリスト
trajectory = [(x, y)]

# AdamWによる最適化
for t in range(1, 51):
    grad = gradient(x, y)
    x, y, m, v, m_hat, v_hat = adamw_update(x, y, m, v, m_hat, v_hat, grad, t, learning_rate, beta1, beta2, epsilon, weight_decay)
    trajectory.append((x, y))

# 等高線図の作成
x_range = np.linspace(-10, 10, 400)
y_range = np.linspace(-10, 10, 400)
X, Y = np.meshgrid(x_range, y_range)
Z = loss_function(X, Y)

plt.figure(figsize=(10, 8))
contour = plt.contour(X, Y, Z, levels=20, cmap='viridis')
plt.clabel(contour, inline=True, fontsize=8)

# 軌跡のプロット
trajectory = np.array(trajectory)
plt.plot(trajectory[:, 0], trajectory[:, 1], 'ro-', label='AdamW Path')

# 始点と終点をマーク
plt.plot(x_start, y_start, 'go', markersize=10, label='Start')
plt.plot(trajectory[-1, 0], trajectory[-1, 1], 'mo', markersize=10, label='End')

plt.title('AdamW Optimizer Behavior')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()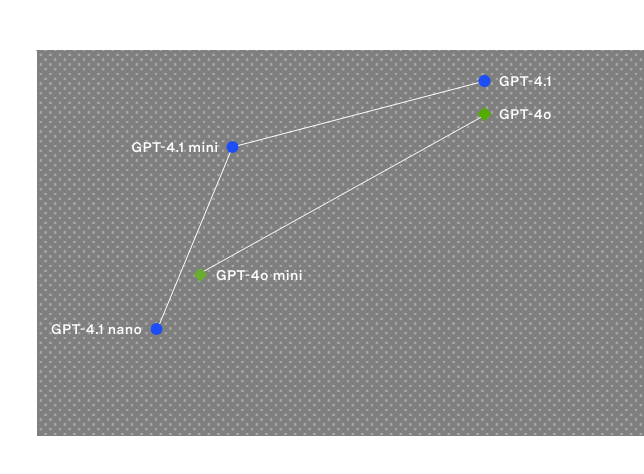

AdamWのコーディング例（PyTorch）：

import torch.optim as optim

# AdamWオプティマイザ
optimizer = optim.AdamW(
    net.parameters(),
    lr=1e-3,
    weight_decay=0.01,  # 重み減衰
    betas=(0.9, 0.999),
    eps=1e-8
)

AdaBelief (2020)

AdaBelief は、Adamのモーメント推定を改良し、勾配の分布をより厳密に反映することで性能を向上させたアルゴリズムです。

一次モーメントの更新式：

$$m_t = \beta_1 m_{t-1} + (1 – \beta_1) g_t$$

二次モーメントの更新式（勾配の差分ベース）：

$$s_t = \beta_2 s_{t-1} + (1 – \beta_2)(g_t – m_t)^2$$

正規化された更新：

$$w_{t+1} = w_t – \alpha \frac{m_t}{\sqrt{s_t} + \epsilon}$$

特徴：

項目内容
精密なモーメント計算勾配とその期待値との差分を活用し、標準的な勾配分散よりも勾配の変動を正確に捉える。
汎化性能の向上勾配の過剰適応（過学習）を抑制し、モデルの汎化性能を高める。
安定性Adamと同様の形式で簡単に利用可能であり、トレーニングの安定性を提供。

利点：

項目内容
過学習の抑制過剰適応を防ぎ、トレーニングデータに依存しすぎないモデルを構築。
適用範囲の広さCNNやRNNなど、多様なタスクに適用可能であり、幅広い応用分野で利用できる。

欠点：

  • AdaBeliefの欠点として、他の手法に比べて計算負荷が若干高く、タスクによってはAdamと同等または劣る場合がある点が挙げられます。また、ハイパーパラメータ調整が必要です。

適用例：

  • ディープラーニングでの使用
    • CNN、RNNに使用可能。
  • その他の特徴
    • 汎化性能を重視したタスク（例: 画像分類、テキスト分類）やスパースデータの学習に最適。
    • 過学習のリスクが高いタスクで効果的。
    • 勾配の変動を精密に捉えるため、安定性が求められるモデルで有用。

論文

AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients
Most popular optimizers for deep learning can be broadly categorized as adaptive methods (e.g. Adam) and accelerated sch...
arxiv.org
  • AdaBeliefは、勾配の予測値（EMA）と実際の値のズレを「信頼度」として評価し、その信頼度に応じてステップサイズを調整する新しい仕組みを提案しています。この方法により、Adamの速い収束性、SGDの優れた汎化性能、安定した学習の3つを同時に実現する画期的な手法です。
  • AdaBeliefは、Adamと比較して追加のハイパーパラメータを導入せず、計算コストもほぼ同等です。
  • AdaBeliefは、画像分類、言語モデリング、GANトレーニングなど幅広いタスクで優れた性能を発揮しました。特にGANの学習では、従来の手法に比べて高い安定性と生成品質を実現し、既存の課題を効果的に克服しています。

動作イメージ

  • AdaBeliefの動作イメージは、「勾配の変化を信頼度（Belief）として捉え、それに基づいて更新量を調整する」というものです。これにより、過学習を抑制しつつ、適応的で効率的な学習が可能になります。特に勾配の変化が多い不安定なタスクで効果を発揮します。
  • 凹凸や急カーブが多い道では慎重に、直線の滑らかな道ではスピードを上げる車の運転。環境の状況に応じて速度を調整をするようなイメージ
import numpy as np
import matplotlib.pyplot as plt

def func(x, y):
    """二次関数（楕円形状）の定義"""
    return 0.1 * x**2 + y**2

def grad_func(x, y):
    """関数の勾配を計算"""
    grad_x = 0.2 * x
    grad_y = 2 * y
    return np.array([grad_x, grad_y])

def adabelief_optimization(x_init, y_init, learning_rate=0.1, beta1=0.9, beta2=0.999, epsilon=1e-8, steps=50):
    """AdaBelief最適化の実行"""
    x, y = x_init, y_init
    m = np.array([0.0, 0.0])  # 一階モーメント
    s = np.array([0.0, 0.0])  # 二階モーメント
    trajectory = [(x, y)]
    update_history = []
    
    for t in range(1, steps + 1):
        grad = grad_func(x, y)
        
        # モーメントの更新
        m = beta1 * m + (1 - beta1) * grad
        s = beta2 * s + (1 - beta2) * (grad - m) ** 2
        
        # バイアス補正
        m_hat = m / (1 - beta1 ** t)
        s_hat = s / (1 - beta2 ** t)
        
        # パラメータの更新
        update = learning_rate * m_hat / (np.sqrt(s_hat) + epsilon)
        x = x - update[0]
        y = y - update[1]
        
        # 軌跡の記録
        trajectory.append((x, y))
        update_history.append(update.copy())
    
    return np.array(trajectory), np.array(update_history)

def plot_contour_with_trajectory(func, trajectory, update_history, levels=20):
    """等高線と最適化の軌跡をプロット"""
    x_range = np.linspace(-10, 10, 400)
    y_range = np.linspace(-10, 10, 400)
    X, Y = np.meshgrid(x_range, y_range)
    Z = func(X, Y)
    
    plt.figure(figsize=(10, 8))
    contour = plt.contour(X, Y, Z, levels=levels, cmap="cool")
    plt.clabel(contour, inline=True, fontsize=8)
    
    # 軌跡のプロット
    plt.plot(trajectory[:, 0], trajectory[:, 1], 'mo-', markersize=5, label="AdaBelief Path")
    
    # 初期点と最終点のマーカー
    plt.scatter(trajectory[0, 0], trajectory[0, 1], color='green', s=100, label='Start')
    plt.scatter(trajectory[-1, 0], trajectory[-1, 1], color='blue', s=100, label='End')
    
    # 矢印を追加して更新ベクトルを示す（間引いて表示）
    for i in range(0, len(trajectory) - 1, 5):
        plt.arrow(trajectory[i, 0], trajectory[i, 1],
                  update_history[i, 0], update_history[i, 1],
                  head_width=0.3, head_length=0.3, fc='k', ec='k')
    
    plt.title("AdaBelief Optimization Trajectory")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.grid(True)
    plt.show()

# パラメータの設定
learning_rate = 0.1
beta1 = 0.9
beta2 = 0.999
epsilon = 1e-8
steps = 50
x_init, y_init = -8.0, 4.0

# 最適化の実行
trajectory, update_history = adabelief_optimization(
    x_init, y_init,
    learning_rate=learning_rate,
    beta1=beta1,
    beta2=beta2,
    epsilon=epsilon,
    steps=steps
)

# プロットの作成
plot_contour_with_trajectory(func, trajectory, update_history)

AdaBeliefのコーディング例（PyTorch）：

pip install adabelief-pytorch
# AdaBeliefオプティマイザの設定
optimizer = AdaBelief(model.parameters(), lr=0.01)

AdaBeliefのコーディング例_2）

rangerとadabeliefを使うことができます。

pip install ranger-adabelief
from ranger_adabelief import Ranger, AdaBelief

# AdaBeliefの初期化
optimizer = AdaBelief(model.parameters(), lr=0.01, eps=1e-16, weight_decay=1e-4, rectify=False)

RAdam (2019)

RAdam は、Adamの適応的学習率を改良し、初期段階での学習の安定性を向上させた手法です。

学習率補正：

$$\rho_t = \frac{2}{1 – \beta_2} – 2t + 2$$

$$\text{修正学習率} = \alpha \sqrt{\frac{\rho_t – 4}{\rho_t (\rho_t – 2)}}$$

更新式：

$$w_{t+1} = w_t – \text{修正学習率} \cdot \frac{m_t}{\sqrt{v_t} + \epsilon}$$

特徴と利点：

項目内容
初期段階の安定性小さなバッチや不安定な学習初期段階でも収束を安定化し、勾配の不安定さを低減。
汎用性Adamを使用するタスクに容易に適用でき、深いネットワークにも効果的に適用可能。

欠点：

  • RAdamの欠点は、初期の学習安定化に特化しているため、収束速度が他の手法に劣る場合がある点です。また、大規模モデルでは性能改善が限定的な場合があります。

適用例：

  • ディープラーニングでの使用
    • CNN、RNNに使用可能。
  • その他の特徴
    • 深いネットワークや勾配の不安定性が課題となるモデル（例: GAN、BERTなどのNLPタスク）に適用。
    • 特に学習初期段階の不安定性を解消し、収束速度を向上させる。

論文：

On the Variance of the Adaptive Learning Rate and Beyond
The learning rate warmup heuristic achieves remarkable success in stabilizing training, accelerating convergence and imp...
arxiv.org
  • 本論文は、Adamなどの適応的最適化アルゴリズムが学習の初期段階で分散の大きさにより収束が不安定になる問題を明らかにしました。そして、ウォームアップがこの分散を抑える効果を持つことを理論と実験を通じて示しています。
  • 著者らは、適応学習率の分散を補正する新しい手法「RAdam」を提案しました。この手法はウォームアップを使わずに学習の安定性を確保し、言語モデリングや画像分類などの多様なタスクで従来のAdamを上回る成果を示しました。
  • RAdamは、他の学習安定化技術（例: 勾配クリッピング、学習率平滑化）とも組み合わせて使用可能です。

動作イメージ

  • RAdamの動作イメージは、「初期段階で慎重に進み、安定した段階でスムーズに加速する」最適化手法です。これにより、深いネットワークや不安定なタスクでも安定した収束を実現します。
import numpy as np
import matplotlib.pyplot as plt

# 損失関数（例：楕円形）
def loss_function(x, y):
    return 0.1 * x**2 + y**2

# 損失関数の勾配
def gradient(x, y):
    return np.array([0.2 * x, 2 * y])

# RAdamのパラメータ更新関数
def radam_update(x, y, m, v, m_hat, v_hat, grad, t, learning_rate, beta1, beta2, epsilon, weight_decay):
    # 重み減衰を適用した勾配
    grad_wd = grad + weight_decay * np.array([x, y])

    # 一次モーメントの更新
    m = beta1 * m + (1 - beta1) * grad_wd
    # 二次モーメントの更新
    v = beta2 * v + (1 - beta2) * (grad_wd ** 2)

    # バイアス補正
    m_hat = m / (1 - beta1 ** t)
    v_hat = v / (1 - beta2 ** t)

    # SMA計算
    rho_inf = 2 / (1 - beta2) - 1
    rho_t = rho_inf - 2 * t * beta2 ** t / (1 - beta2 ** t)

    # 更新量の計算
    if rho_t > 4:
        r = np.sqrt(((rho_t - 4) * (rho_t - 2) * rho_inf) / ((rho_inf - 4) * (rho_inf - 2) * rho_t))
        update = r * m_hat / (np.sqrt(v_hat) + epsilon)
    else:
        update = m_hat

    # パラメータの更新
    x -= learning_rate * update[0]
    y -= learning_rate * update[1]

    return x, y, m, v, m_hat, v_hat

# パラメータ
x_start = -8
y_start = 9
learning_rate = 0.5  # 学習率
beta1 = 0.9  # 一次モーメントの減衰率
beta2 = 0.999  # 二次モーメントの減衰率
epsilon = 1e-8  # ゼロ除算を防ぐための小さな値
weight_decay = 0.01  # 重み減衰

# 初期位置
x = x_start
y = y_start

# モーメントの初期化
m = np.array([0.0, 0.0])
v = np.array([0.0, 0.0])
m_hat = np.array([0.0, 0.0])
v_hat = np.array([0.0, 0.0])

# 軌跡を保存するリスト
trajectory = [(x, y)]

# RAdamによる最適化
for t in range(1, 51):
    grad = gradient(x, y)
    x, y, m, v, m_hat, v_hat = radam_update(x, y, m, v, m_hat, v_hat, grad, t, learning_rate, beta1, beta2, epsilon, weight_decay)
    trajectory.append((x, y))

# 等高線図の作成
x_range = np.linspace(-10, 10, 400)
y_range = np.linspace(-10, 10, 400)
X, Y = np.meshgrid(x_range, y_range)
Z = loss_function(X, Y)

plt.figure(figsize=(10, 8))
contour = plt.contour(X, Y, Z, levels=20, cmap='viridis')
plt.clabel(contour, inline=True, fontsize=8)

# 軌跡のプロット
trajectory = np.array(trajectory)
plt.plot(trajectory[:, 0], trajectory[:, 1], 'ro-', label='RAdam Path')

# 始点と終点をマーク
plt.plot(x_start, y_start, 'go', markersize=10, label='Start')
plt.plot(trajectory[-1, 0], trajectory[-1, 1], 'mo', markersize=10, label='End')

plt.title('RAdam Optimizer Behavior')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

RAdamのコーディング例（PyTorch）：

radam はPyTorchの標準ライブラリには含まれていないため、サードパーティの実装を使用する必要があります。まず、RAdamオプティマイザを自分で実装します。

別ファイルにradam.pyを作成し、from radam import RAdamを使用してradam.pyからRAdamクラスをインポートします。

  • radam.py
import torch
from torch.optim.optimizer import Optimizer
import math

class RAdam(Optimizer):
    def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), eps=1e-8, weight_decay=0, degenerated_to_sgd=True):
        if not 0.0 <= lr:
            raise ValueError("Invalid learning rate: {}".format(lr))
        if not 0.0 <= eps:
            raise ValueError("Invalid epsilon value: {}".format(eps))
        if not 0.0 <= betas[0] < 1.0:
            raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))
        if not 0.0 <= betas[1] < 1.0:
            raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))

        self.degenerated_to_sgd = degenerated_to_sgd
        if isinstance(params, (list, tuple)) and len(params) > 0 and isinstance(params[0], dict):
            for param in params:
                if 'betas' in param and (param['betas'][0] != betas[0] or param['betas'][1] != betas[1]):
                    param['buffer'] = [[None, None, None] for _ in range(10)]
        defaults = dict(lr=lr, betas=betas, eps=eps, weight_decay=weight_decay, buffer=[[None, None, None] for _ in range(10)])
        super(RAdam, self).__init__(params, defaults)

    def __setstate__(self, state):
        super(RAdam, self).__setstate__(state)

    def step(self, closure=None):

        loss = None
        if closure is not None:
            loss = closure()

        for group in self.param_groups:

            for p in group['params']:
                if p.grad is None:
                    continue
                grad = p.grad.data.float()
                if grad.is_sparse:
                    raise RuntimeError('RAdam does not support sparse gradients')

                p_data_fp32 = p.data.float()

                state = self.state[p]

                if len(state) == 0:
                    state['step'] = 0
                    state['exp_avg'] = torch.zeros_like(p_data_fp32)
                    state['exp_avg_sq'] = torch.zeros_like(p_data_fp32)
                else:
                    state['exp_avg'] = state['exp_avg'].type_as(p_data_fp32)
                    state['exp_avg_sq'] = state['exp_avg_sq'].type_as(p_data_fp32)

                exp_avg, exp_avg_sq = state['exp_avg'], state['exp_avg_sq']
                beta1, beta2 = group['betas']

                exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1 - beta2)
                exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)

                state['step'] += 1
                buffered = group['buffer'][int(state['step'] % 10)]
                if state['step'] == buffered[0]:
                    N_sma, step_size = buffered[1], buffered[2]
                else:
                    buffered[0] = state['step']
                    beta2_t = beta2 ** state['step']
                    N_sma_max = 2 / (1 - beta2) - 1
                    N_sma = N_sma_max - 2 * state['step'] * beta2_t / (1 - beta2_t)
                    buffered[1] = N_sma

                    # more conservative since it's an approximated value
                    if N_sma >= 5:
                        step_size = math.sqrt((1 - beta2_t) * (N_sma - 4) / (N_sma_max - 4) * (N_sma - 2) / N_sma * N_sma_max / (N_sma_max - 2)) / (1 - beta1 ** state['step'])
                    elif self.degenerated_to_sgd:
                        step_size = 1.0 / (1 - beta1 ** state['step'])
                    else:
                        step_size = -1
                    buffered[2] = step_size

                # more conservative since it's an approximated value
                if N_sma >= 5:
                    if group['weight_decay'] != 0:
                        p_data_fp32.add_(p_data_fp32, alpha=-group['weight_decay'] * group['lr'])
                    denom = exp_avg_sq.sqrt().add_(group['eps'])
                    p_data_fp32.addcdiv_(exp_avg, denom, value=-step_size * group['lr'])
                    p.data.copy_(p_data_fp32)
                elif step_size > 0:
                    if group['weight_decay'] != 0:
                        p_data_fp32.add_(p_data_fp32, alpha=-group['weight_decay'] * group['lr'])
                    p_data_fp32.add_(exp_avg, alpha=-step_size * group['lr'])
                    p.data.copy_(p_data_fp32)

        return loss
from radam import RAdam  # radam.pyからRAdamクラスをインポート

optimizer = RAdam(model.parameters(), lr=0.001)

その他の方法としてサードパーティのライブラリを使用することでRAdamをインポートし、使用することが可能です。

torch-optimizer：

GitHub - jettify/pytorch-optimizer: torch-optimizer -- collection of optimizers for Pytorch
torch-optimizer -- collection of optimizers for Pytorch - jettify/pytorch-optimizer
github.com
 
pip install torch_optimizer
import torch_optimizer as optim

# RAdamオプティマイザ
radam = RAdam(net.parameters(), lr=0.01)

LookAhead Optimizer(2019)

LookAhead Optimizerは、パラメータの更新に「現在の進行方向」と「過去の位置」の関係を取り入れることで、安定性と収束速度を向上させた最適化手法です。他の最適化アルゴリズム（例: Adam、RAdam）と組み合わせて使用することで、長期的な方向性を取り入れた更新が可能になります。

内側の更新式 (Inner Update)：

  • 内側の最適化アルゴリズム（例: Adam）を用いて $k$ ステップ進行。

$$w_{\text{interim}} = w_t + \Delta w \quad (\text{通常の最適化アルゴリズムによる更新})$$

外側の更新式 (Outer Update)：

  • 過去の位置 $w_t$​ と内側の更新結果 $w_{\text{interim}}$​ を組み合わせて最終的な更新を行います。

$$w_{t+1} = w_t + \alpha (w_{\text{interim}} – w_t)$$

  • $α$： LookAheadのステップサイズ（一般的には $\alpha = 0.5$ が使用される）。
  • $w_{\text{interim}}$：内側の更新結果（複数ステップ分のパラメータ更新の累積）。

特徴：

項目内容
長期的な方向性の活用短期的な更新だけでなく、過去の位置との比較を通じて方向性を安定化し、より効率的な更新を実現。
組み合わせ可能AdamやRAdam、SGDなど、他の最適化アルゴリズムに追加して使用することが可能。
安定性の向上局所的な振動を抑え、安定した収束を実現。

利点：

項目内容
収束速度の向上長期的な視点での更新により、より効率的に最適解へ到達。
安定性局所的な最適解に陥りにくく、勾配のばらつきを抑える効果がある。
汎用性他のアルゴリズムと簡単に統合可能で、幅広いタスクに適用できる。

欠点：

  • LookAhead Optimizerの欠点は、計算コストの増加、ハイパーパラメータ調整の難しさ、内側の最適化アルゴリズムへの依存、効果が限定的な場合があることです。

適用例：

  • ディープラーニングでの使用
    • 他の最適化手法（例: Adam、RAdam）と組み合わせてCNN、RNNで使用可能。
  • その他の特徴
    • 局所的な勾配の振動を抑え、収束を安定化させる。
    • 強化学習（RL）や不安定なタスク（例: GAN）で効果を発揮。
    • 長期的な学習方向を修正する手法として、より安定した学習を提供。

論文：

Lookahead Optimizer: k steps forward, 1 step back
The vast majority of successful deep neural networks are trained using variants of stochastic gradient descent (SGD) alg...
arxiv.org
  • Lookaheadは、2種類の重み（高速重みと低速重み）を使い分けることで、既存の最適化アルゴリズムの分散を抑え、学習を安定させる新しい手法です。既存の手法と組み合わせることで、収束速度も向上します。
  • Lookaheadは、SGDやAdamといった従来のアルゴリズムに適用できる汎用性の高い手法です。CIFARやImageNetなどのデータセットで、収束の速さと精度の向上が実証されており、ハイパーパラメータの調整が簡単で、実装コストも低いのが特徴です。
  • SWA（Stochastic Weight Averaging）やPolyak平均化といった手法よりも高速な収束と優れた汎化性能を実現しました。
  • ResNet-50やResNet-152などのさまざまなアーキテクチャおよびデータセットでテストされ、わずかな調整でパフォーマンス向上を達成しました。

動作イメージ

  • LookAhead Optimizerの動作イメージは、「内側の更新で進み、外側の更新で方向性を見直す」というものです。この2段階の更新により、収束速度と安定性が向上し、多くのタスクで性能を改善できます。他の最適化手法との併用が可能である点も、大きな利点です。
  • 登山者が時々振り返り、全体の進行方向を確認しながら進む。これにより、より効率的に目標に近づく。
    • 短期的な進行（内側の更新）: 局所的な勾配を利用してパラメータを更新。
    • 長期的な方向性の見直し（外側の更新）: 過去の位置を基に大局的な進行方向を調整。
import numpy as np
import matplotlib.pyplot as plt

def loss_function(x, y):
  """損失関数（例：楕円形）"""
  return 0.1 * x**2 + y**2

def gradient(x, y):
  """損失関数の勾配"""
  return np.array([0.2 * x, 2 * y])

def fast_optimizer_step(x, y, learning_rate):
  """高速オプティマイザのステップ（例：Adam）"""
  grad = gradient(x, y)
  # 簡略化のため、Adamの完全な実装ではなく、単純な勾配降下法を使用
  return x - learning_rate * grad[0], y - learning_rate * grad[1]

def slow_optimizer_step(x_fast, x_slow, alpha):
  """低速オプティマイザのステップ"""
  return x_slow + alpha * (x_fast - x_slow)

# パラメータ
x_start = -8
y_start = 9
learning_rate = 0.5  # 高速オプティマイザの学習率
alpha = 0.8  # 低速オプティマイザの更新率
k = 5  # 高速オプティマイザのステップ数

# 初期位置
x_slow = x_start
y_slow = y_start
x_fast = x_start
y_fast = y_start

# 軌跡を保存するリスト
slow_trajectory = [(x_slow, y_slow)]
fast_trajectory = [(x_fast, y_fast)]

# Lookaheadの動作
for i in range(20):  # Lookaheadの反復回数
  # 高速オプティマイザのステップをk回実行
  for _ in range(k):
    x_fast, y_fast = fast_optimizer_step(x_fast, y_fast, learning_rate)
    fast_trajectory.append((x_fast, y_fast))

  # 低速オプティマイザのステップを1回実行
  x_slow = slow_optimizer_step(x_fast, x_slow, alpha)
  y_slow = slow_optimizer_step(y_fast, y_slow, alpha)
  slow_trajectory.append((x_slow, y_slow))

  # 高速オプティマイザの位置を低速オプティマイザの位置にリセット
  x_fast = x_slow
  y_fast = y_slow

# 等高線図の作成
x = np.linspace(-10, 10, 400)
y = np.linspace(-10, 10, 400)
X, Y = np.meshgrid(x, y)
Z = loss_function(X, Y)

plt.figure(figsize=(10, 8))
contour = plt.contour(X, Y, Z, levels=20, cmap='viridis')
plt.clabel(contour, inline=True, fontsize=8)

# 軌跡のプロット
slow_trajectory = np.array(slow_trajectory)
fast_trajectory = np.array(fast_trajectory)
plt.plot(slow_trajectory[:, 0], slow_trajectory[:, 1], 'bo-', label='Slow Weights (Lookahead Path)')
plt.plot(fast_trajectory[:, 0], fast_trajectory[:, 1], 'ro-', label='Fast Weights (Inner Loop)', alpha=0.5)

# 矢印で方向を表示（低速オプティマイザのみ）
for i in range(len(slow_trajectory) - 1):
  plt.arrow(slow_trajectory[i, 0], slow_trajectory[i, 1],
            slow_trajectory[i+1, 0] - slow_trajectory[i, 0],
            slow_trajectory[i+1, 1] - slow_trajectory[i, 1],
            head_width=0.3, head_length=0.3, fc='b', ec='b')

# 始点と終点をマーク
plt.plot(x_start, y_start, 'go', markersize=10, label='Start')
plt.plot(slow_trajectory[-1, 0], slow_trajectory[-1, 1], 'mo', markersize=10, label='End')

plt.title('Lookahead Optimizer Behavior')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

LookAheadのコーディング例（PyTorch）：

LookAheadの場合もRAdam同様、サードパーティライブラリを使うか自分で実装するかです。今回はサードパーティライブラリを使います。

torch-optimizer：

GitHub - jettify/pytorch-optimizer: torch-optimizer -- collection of optimizers for Pytorch
torch-optimizer -- collection of optimizers for Pytorch - jettify/pytorch-optimizer
github.com
 
pip install torch_optimizer
import torch_optimizer as optim

# RAdamオプティマイザ
radam = RAdam(net.parameters(), lr=0.01)

# Lookaheadオプティマイザ (torch_optimizerを使用)
optimizer = optim.Lookahead(radam, k=5, alpha=0.5)

Ranger (2019)

Ranger は、RAdam (Rectified Adam) と LookAhead Optimizer を組み合わせた最適化アルゴリズムです。RAdamの安定性とLookAheadの長期的な方向性の改善を取り入れることで、学習の安定性と収束速度をさらに向上させます。

特徴：

項目内容
RAdamの安定性勾配の振動を抑え、特に初期段階での学習の安定性を向上。高い学習率を安全に設定可能。
LookAheadの長期視点局所的な振動や不安定性をさらに緩和し、長期的な方向性を加味することで局所最適解に陥りにくい。
汎用性CNNやRNN、NLPなど、多様なタスクで効果を発揮。

利点：

項目内容
収束速度の向上RAdamの高速収束特性に加え、LookAheadによる全体的な方向性の見直しでさらに速度を向上。
安定性勾配の変動が大きいタスクでも、スムーズな学習が可能。
過学習の抑制局所的な最適解への過剰適応を防ぎ、汎化性能が向上。

欠点：

  • Ranger Optimizerは、RAdamとLookAheadの組み合わせにより計算コストが増加し、ハイパーパラメータ（更新回数 $k$ やステップサイズ $\alpha$）の調整が必要です。学習が安定しているタスクでは利点が限定される場合があり、複雑なタスクでは過学習リスクが高まる可能性があるため、追加の正則化が求められることがあります。

適用例：

  • ディープラーニングでの使用
    • CNN、RNNに使用可能。
  • その他の特徴
    • 大規模データセットや複雑なモデルで優れた安定性と収束速度を発揮。
    • RAdamの安定性とLookAheadの長期視点を組み合わせており、NLPや画像認識など幅広いタスクに適用可能。
    • 高い汎化性能と安定性が求められる場面で最適。

論文：

GitHub - lessw2020/Ranger-Deep-Learning-Optimizer: Ranger - a synergistic optimizer using RAdam (Rectified Adam), Gradient Centralization and LookAhead in one codebase
Ranger - a synergistic optimizer using RAdam (Rectified Adam), Gradient Centralization and LookAhead in one codebase - l...
github.com
New Deep Learning Optimizer, Ranger: Synergistic combination of RAdam + LookAhead for the best of…
A new paper in part by the famed deep learning researcher Geoffrey Hinton introduces the LookAhead optimizer(“LookAhead ...
lessw.medium.com
  • Rangerは、FastAIのグローバルリーダーボードで12のトップパフォーマンスを記録するなど、実世界でのディープラーニングタスクでその性能が証明されています。
  • Rangerは、多様なディープラーニングタスクに適用可能で、特に大規模データセットや複雑なモデル構造で高い性能を発揮します。

動作イメージ

  • Rangerは、RAdamとLookAheadの連携により、短期的な学習の効率化と長期的な安定性を同時に実現するアルゴリズムです。この動作フローにより、モデルは局所的な最適解に陥りにくく、深いネットワークや不安定なタスクで優れた性能を発揮します。
  • RAdamの役割
    • 小刻みに進む登山者のように、短期的な方向性に基づいて慎重に進む。
  • LookAheadの役割
    • 時々立ち止まり、地図を見て全体の方向性を確認し、最適なルートを修正する。
import numpy as np
import matplotlib.pyplot as plt
import torch
from ranger import Ranger  # Ranger-Deep-Learning-Optimizerからインポート

# 損失関数（例：楕円形）
def loss_function(x, y):
    return 0.1 * x**2 + y**2

# 損失関数の勾配
def gradient(x, y):
    return np.array([0.2 * x, 2 * y])

# パラメータ
x_start = -8
y_start = 9
learning_rate = 0.5  # 高速オプティマイザの学習率
alpha = 0.8  # 低速オプティマイザの更新率
k = 5  # 高速オプティマイザのステップ数

# 初期位置（テンソルとして扱う）
x_slow = torch.tensor([x_start], dtype=torch.float32, requires_grad=True)
y_slow = torch.tensor([y_start], dtype=torch.float32, requires_grad=True)
x_fast = torch.tensor([x_start], dtype=torch.float32, requires_grad=True)
y_fast = torch.tensor([y_start], dtype=torch.float32, requires_grad=True)

# Rangerオプティマイザのセットアップ
params = [{'params': [x_fast, y_fast]}]
optimizer = Ranger(params, lr=learning_rate, alpha=alpha, k=k, betas=(0.95, 0.999))

# 軌跡を保存するリスト
slow_trajectory = [(x_slow.item(), y_slow.item())]
fast_trajectory = [(x_fast.item(), y_fast.item())]

# Lookaheadの動作
for i in range(20):  # Lookaheadの反復回数
    # 高速オプティマイザのステップをk回実行
    for _ in range(k):
        loss = loss_function(x_fast, y_fast)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()
        fast_trajectory.append((x_fast.item(), y_fast.item()))

    # 低速オプティマイザのステップを1回実行
    x_slow = x_slow + alpha * (x_fast - x_slow)
    y_slow = y_slow + alpha * (y_fast - y_slow)
    slow_trajectory.append((x_slow.item(), y_slow.item()))

    # 高速オプティマイザの位置を低速オプティマイザの位置にリセット
    x_fast.data.copy_(x_slow.data)
    y_fast.data.copy_(y_slow.data)

# 等高線図の作成
x = np.linspace(-10, 10, 400)
y = np.linspace(-10, 10, 400)
X, Y = np.meshgrid(x, y)
Z = loss_function(torch.tensor(X), torch.tensor(Y))

plt.figure(figsize=(10, 8))
contour = plt.contour(X, Y, Z.numpy(), levels=20, cmap='viridis')
plt.clabel(contour, inline=True, fontsize=8)

# 軌跡のプロット
slow_trajectory = np.array(slow_trajectory)
fast_trajectory = np.array(fast_trajectory)
plt.plot(slow_trajectory[:, 0], slow_trajectory[:, 1], 'bo-', label='Slow Weights (Lookahead Path)')
plt.plot(fast_trajectory[:, 0], fast_trajectory[:, 1], 'ro-', label='Fast Weights (Inner Loop)', alpha=0.5)

# 矢印で方向を表示（低速オプティマイザのみ）
for i in range(len(slow_trajectory) - 1):
    plt.arrow(slow_trajectory[i, 0], slow_trajectory[i, 1],
              slow_trajectory[i+1, 0] - slow_trajectory[i, 0],
              slow_trajectory[i+1, 1] - slow_trajectory[i, 1],
              head_width=0.3, head_length=0.3, fc='b', ec='b')

# 始点と終点をマーク
plt.plot(x_start, y_start, 'go', markersize=10, label='Start')
plt.plot(slow_trajectory[-1, 0], slow_trajectory[-1, 1], 'mo', markersize=10, label='End')

plt.title('Ranger Optimizer Behavior')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

Rangerのコーディング例（PyTorch）：

Rangerのサードパーティライブラリは下記からインポートします。

pip install git+https://github.com/lessw2020/Ranger-Deep-Learning-Optimizer.git
from ranger import Ranger  # ライブラリからRangerをインポート

# Ranger Optimizerの設定
optimizer = Ranger(model.parameters(), lr=0.01)

Rangerのコーディング例_2（PyTorch）：

rangerとadabeliefのどちらかを使うことができます。

pip install ranger-adabelief
from ranger_adabelief import Ranger, AdaBelief

# Rangerの初期化
ranger_optimizer = Ranger(model.parameters(), lr=0.01)

# AdaBeliefの初期化
optimizer = AdaBelief(model.parameters(), lr=0.01, eps=1e-16, weight_decay=1e-4, rectify=False)

Lamb (2019)

Lamb（Layer-wise Adaptive Moments for Batch Training）は、大規模バッチトレーニング向けに設計された最適化アルゴリズムで、各層のパラメータスケールに応じた学習率を調整することで、安定性と収束速度を両立します。特に、BERTやGPTなどの大規模言語モデルで効果を発揮します。

アルゴリズムの詳細

  • 勾配のモーメント計算
    • Lambは、Adamと同様に勾配の一次モーメントと二次モーメントを計算します。

$$m_t = \beta_1 m_{t-1} + (1 – \beta_1) g_t$$

$$v_t = \beta_2 v_{t-1} + (1 – \beta_2) g_t^2$$

  • モーメントのバイアス補正
    • Adamと同様にバイアス補正を行います。

$$\hat{m}_t = \frac{m_t}{1 – \beta_1^t}$$

$$\hat{v}_t = \frac{v_t}{1 – \beta_2^t}$$

  • 勾配の正規化
    • 更新方向を正規化して、層ごとに勾配のスケールを調整します。

$$r_t = \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}$$

  • パラメータの正規化
    • Lambでは、更新方向 $r_t$​ とパラメータ $w_t$​ の両方を正規化し、それらの比率を取ることでスケールに基づいた更新を行います。

$$\lambda_t = \frac{\|w_t\|}{\|r_t\|}$$

  • 重み更新

$$w_{t+1} = w_t – \alpha \cdot \lambda_t \cdot r_t$$

特徴表記説明
勾配の一次モーメント$m_t$勾配の一次モーメント
勾配の二次モーメント$v_t$勾配の二次モーメント
現在の勾配$g_t$現在の勾配
モーメントの減衰率$\beta_1, \beta_2$モーメントの減衰率（通常 ($\beta_1 = 0.9,$ $\beta_2 = 0.999$)）
ゼロ割りを防ぐための小さな値$\epsilon$ゼロ割りを防ぐための小さな値（通常 ($1 \times 10^{-8})$）

特徴：

項目内容
スケール調整各層のパラメータに適応的なスケール調整を行い、層ごとの学習率を自動的に調整。
大規模バッチ対応大規模バッチサイズ（例: 数千以上）でのトレーニングに適し、分散トレーニングでの収束速度を向上。
安定性の向上勾配とパラメータを正規化することで過剰な更新を防ぎ、安定した学習を実現。

利点：

項目内容
大規模分散トレーニングに適用可能BERTやGPTのような大規模モデルで高い収束速度と安定性を発揮。
スケール不変性パラメータのスケールに依存せず、各層が適切に学習できるよう調整。
Adamとの互換性Adamをベースにしているため、既存のディープラーニングタスクに簡単に導入可能。

欠点：

  • Lamb Optimizerの欠点は、計算コストの増加や小バッチサイズでの性能低下、ハイパーパラメータ調整の難しさが挙げられます。また、大規模モデルや分散トレーニングに特化しているため、小規模データセットや単一GPUでは恩恵が少なく、実装の複雑さから初心者には扱いにくい可能性があります。

適用例：

  • ディープラーニングでの使用
    • CNN、RNNに使用可能。
  • その他の用途
    • BERTやGPTなどの大規模言語モデルの学習。
    • 大規模データセットを用いたCNNトレーニング。
    • 複数GPUやTPUを用いた大規模トレーニング。

論文：

Large Batch Optimization for Deep Learning: Training BERT in 76 minutes
Training large deep neural networks on massive datasets is computationally very challenging. There has been recent surge...
arxiv.org
  • LAMBオプティマイザの導入により、BERTのトレーニング時間が3日からわずか76分に短縮されました。さらに、大規模なバッチサイズ（最大32,868）でも性能を維持しながら効率的に学習を進められるようになりました。
  • LAMBはレイヤーごとに適応する学習率を採用し、従来の手法で問題となっていたBERTなどの注意機構モデルの性能低下を解消しました。この方法により、さまざまなモデルで使える汎用性と安定した収束性が実現しました。
  • LARSのような既存手法はタスクごとに性能が一貫しない問題がありましたが、LAMBはこれを克服しました。

動作イメージ

Lambの動作イメージは、層ごとのスケールを考慮して学習率を調整する点にあります。この仕組みは、大規模バッチトレーニングや複雑なモデルでの安定性向上と高速収束を可能にします。層の特性を活かした柔軟な学習を実現する最適化アルゴリズムです。

import numpy as np
import matplotlib.pyplot as plt
import torch

# 損失関数（例：楕円形）
def loss_function(x, y):
    return 0.1 * x**2 + y**2

# 損失関数の勾配
def gradient(x, y):
    return np.array([0.2 * x, 2 * y])

# LAMBのパラメータ更新関数
def lamb_update(x, y, m, v, m_hat, v_hat, grad, t, learning_rate, beta1, beta2, epsilon, weight_decay):
    grad = grad + weight_decay * np.array([x, y])

    m = beta1 * m + (1 - beta1) * grad
    v = beta2 * v + (1 - beta2) * (grad ** 2)

    m_hat = m / (1 - beta1 ** t)
    v_hat = v / (1 - beta2 ** t)

    w = np.array([x, y])
    w_norm = np.linalg.norm(w)
    update_norm = np.linalg.norm(m_hat / (np.sqrt(v_hat) + epsilon))
    
    trust_ratio = 1.0
    if w_norm > 0 and update_norm > 0:
        trust_ratio = w_norm / update_norm

    x -= learning_rate * trust_ratio * m_hat[0] / (np.sqrt(v_hat[0]) + epsilon)
    y -= learning_rate * trust_ratio * m_hat[1] / (np.sqrt(v_hat[1]) + epsilon)

    return x, y, m, v, m_hat, v_hat

# パラメータ
x_start = -8
y_start = 9
learning_rate = 0.1  # 学習率
beta1 = 0.9  # 一次モーメントの減衰率
beta2 = 0.999  # 二次モーメントの減衰率
epsilon = 1e-8  # ゼロ除算を防ぐための小さな値
weight_decay = 0.01  # 重み減衰

# 初期位置
x = x_start
y = y_start

# モーメントの初期化
m = np.array([0.0, 0.0])
v = np.array([0.0, 0.0])
m_hat = np.array([0.0, 0.0])
v_hat = np.array([0.0, 0.0])

# 軌跡を保存するリスト
trajectory = [(x, y)]

# LAMBによる最適化
for t in range(1, 51):
    grad = gradient(x, y)
    x, y, m, v, m_hat, v_hat = lamb_update(x, y, m, v, m_hat, v_hat, grad, t, learning_rate, beta1, beta2, epsilon, weight_decay)
    trajectory.append((x, y))

# 等高線図の作成
x_range = np.linspace(-10, 10, 400)
y_range = np.linspace(-10, 10, 400)
X, Y = np.meshgrid(x_range, y_range)
Z = loss_function(X, Y)

plt.figure(figsize=(10, 8))
contour = plt.contour(X, Y, Z, levels=20, cmap='viridis')
plt.clabel(contour, inline=True, fontsize=8)

# 軌跡のプロット
trajectory = np.array(trajectory)
plt.plot(trajectory[:, 0], trajectory[:, 1], 'ro-', label='LAMB Path')

# 始点と終点をマーク
plt.plot(x_start, y_start, 'go', markersize=10, label='Start')
plt.plot(trajectory[-1, 0], trajectory[-1, 1], 'mo', markersize=10, label='End')

plt.title('LAMB Optimizer Behavior')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

LAMBのコーディング例（PyTorch）：

pip install pytorch-optimizer
from pytorch_optimizer import Lamb

# Lambオプティマイザ
optimizer = Lamb(
    net.parameters(),
    lr=1e-3,
    weight_decay=0.01,
    betas=(0.9, 0.999),
    eps=1e-8,
)

LAMBのコーディング例2）

pip install git+https://github.com/cybertronai/pytorch-lamb.git
from pytorch_lamb import Lamb

# Lambオプティマイザ（Lookaheadは使用しない）
optimizer = Lamb(
    net.parameters(),
    lr=1e-3,
    weight_decay=0.01,
    betas=(0.9, 0.999),
    eps=1e-8,
)

# Lookaheadオプティマイザでラップする
optimizer = Lookahead(optimizer, k=5, alpha=0.5)

pytorch-lamb リポジトリの Lamb オプティマイザは、Lookahead と併用することで、収束の安定化、ハイパーパラメータ調整の簡略化、汎化性能の向上などの効果が期待できます。

Sophia (2023)

Sophiaは、大規模言語モデル（LLMs）や高度なディープラーニングタスクに特化した最適化アルゴリズムです。2次情報（Hessian行列）を効率的に活用し、勾配更新の方向を正確に調整しながら、計算コストを抑えることに成功しています。

アルゴリズムの詳細

  • 勾配の計算：
    • まず、標準的な勾配降下法と同様に、現在の損失関数 $L$ の勾配 $g_t$​ を計算します。

$$g_t ​= ∇L(w_t)$$

  • Hessian行列の近似
    • Sophiaでは、Hessian行列 $H$ を直接計算するのではなく、効率的な近似を用いて2次情報を取得します。これにより、曲率情報を反映した更新方向が得られます。
    • $\hat{H}$ はヘッセ行列のスケールを簡易化した近似。

$$H \approx \hat{H}$$

  • 勾配更新の方向を調整
    • Hessian行列の近似を利用して、更新方向を次のように計算します
    • $r_t$​: 調整された更新方向。$ϵ$：数値安定性のための小さな値。

$$r_t = \frac{g_t}{\hat{H} + \epsilon}$$

  • 勾配クリッピング
    • 勾配の振動や過大な更新を防ぐため、更新方向 $r_t$​ を一定範囲にクリッピングします。
    • $c$：クリッピング範囲の上限値。

$$r_t = \text{clip}(r_t, -c, c)$$

  • 重みの更新
    • クリッピングされた更新方向に基づいて、パラメータを更新します。

$$w_{t+1} = w_t – \alpha \cdot r_t$$

特徴：

項目内容
効率的な2次情報の利用Hessian行列を直接計算する代わりに近似を使用し、2次情報を活用。
勾配クリッピング勾配の過大な振動を抑え、学習の安定性を向上。
計算コストの低減Hessian行列の近似により、従来の2次最適化手法に比べて計算負荷が軽減。
適応的更新方向2次情報を反映した更新方向により、モデルの収束が高速化。

利点：

項目内容
高速収束2次情報の利用により、少ないステップで損失が収束。
安定性の向上勾配クリッピングにより、過大な更新を防止し学習の安定性を向上。
汎化性能の改善過学習を抑えた更新が可能で、モデルの汎化性能を向上。

欠点：

  • 実装の複雑性
    • 2次情報の近似計算やクリッピング処理の導入が必要。
  • 特定のタスク向け
    • 小規模モデルや単純なタスクでは効果が限定的。

適用例：

  • ディープラーニングでの使用
    • CNN、RNNに使用可能。
  • その他の用途
    • GPT、BERTなど、トランスフォーマーベースの大規模モデル。
    • 画像生成（例: Stable Diffusion）、高度なコンピュータビジョンタスク。
    • 大規模バッチサイズやマルチGPU/TPU環境でのトレーニング。

論文：

Sophia: A Scalable Stochastic Second-order Optimizer for Language Model Pre-training
Given the massive cost of language model pre-training, a non-trivial improvement of the optimization algorithm would lea...
arxiv.org
  • Sophiaは、対角ヘッセ行列の軽量な推定を利用することで、学習スピードをAdamの2倍に向上させました。同時に、ステップ数を半分に抑えながら同等の性能を達成し、大規模言語モデルの事前学習に必要な計算コストと時間を大幅に削減しています。
  • Sophiaは、パラメータごとに異なる曲率にも柔軟に適応し、非凸な問題やヘッセ行列の急激な変化にも対応できます。さらに、損失関数の条件数に依存しない堅実な理論基盤を持ち、安定性と効率性を両立しています。
  • 特に大規模なGPT-2モデルにおいて、AdamWやAdaHessianを上回る性能を発揮。
  • 本研究は言語モデルに焦点を当てていますが、Sophiaはさらなる研究によって、コンピュータビジョンや強化学習などの分野への応用も期待されています。

動作イメージ

  • Sophiaの動作イメージは、損失関数の曲率情報を反映して更新方向を調整し、勾配クリッピングで学習を安定化する点にあります。この設計により、大規模モデルのトレーニングにおいて、高速収束と高い汎化性能を両立しています。
  • Sophiaは、曲がりくねった山道を登る際に、地形の傾斜（曲率）を考慮しながら歩幅（更新方向）を調整する登山者に例えられます。
    • 傾斜が急な場所では歩幅を狭めて慎重に進み、緩やかな場所では歩幅を広げて効率よく進みます。
    • 勾配クリッピングは、滑り落ち（振動）を防ぐための安全装置の役割を果たします。
import numpy as np
import matplotlib.pyplot as plt

# 損失関数（例：楕円形）
def loss_function(x, y):
    return 0.1 * x**2 + y**2

# 損失関数の勾配
def gradient(x, y):
    return np.array([0.2 * x, 2 * y])

# Sophiaのパラメータ更新関数（改善版）
def sophia_update(x, y, h, m, grad, t, learning_rate, beta1, beta2, rho, epsilon, weight_decay):
    # 重み減衰を適用した勾配
    grad_wd = grad + weight_decay * np.array([x, y])

    # Hessian情報の推定（簡略化）
    hessian_diag_estimate = np.abs(grad_wd)
    h = beta2 * h + (1 - beta2) * hessian_diag_estimate

    # 一次モーメントの更新
    m = beta1 * m + (1 - beta1) * grad_wd

    # 更新量の計算
    update = m / np.maximum(rho * h, epsilon)

    # ノルム比の計算（要素ごとに計算）
    w = np.array([x, y])
    w_norm = np.linalg.norm(w)
    update_norm = np.linalg.norm(update)

    trust_ratio = 1.0
    if w_norm > 0 and update_norm > 0:
        trust_ratio = w_norm / update_norm

    # パラメータの更新
    x -= learning_rate * trust_ratio * update[0]
    y -= learning_rate * trust_ratio * update[1]

    return x, y, h, m

# パラメータ
x_start = -8
y_start = 9
learning_rate = 0.05  # 学習率を小さめに設定
beta1 = 0.9  # 一次モーメントの減衰率
beta2 = 0.999  # 二次モーメント（Hessian情報の推定）の減衰率
rho = 0.05  # 更新量のスケーリング係数
epsilon = 1e-8  # ゼロ除算を防ぐための小さな値
weight_decay = 0.01  # 重み減衰

# 初期位置
x = x_start
y = y_start

# Hessian情報の推定値と一次モーメントの初期化
h = np.array([0.0, 0.0])
m = np.array([0.0, 0.0])

# 軌跡を保存するリスト
trajectory = [(x, y)]

# Sophiaによる最適化
for t in range(1, 201):  # ステップ数を増やす
    grad = gradient(x, y)
    x, y, h, m = sophia_update(x, y, h, m, grad, t, learning_rate, beta1, beta2, rho, epsilon, weight_decay)
    trajectory.append((x, y))

# 等高線図の作成
x_range = np.linspace(-10, 10, 400)
y_range = np.linspace(-10, 10, 400)
X, Y = np.meshgrid(x_range, y_range)
Z = loss_function(X, Y)

plt.figure(figsize=(10, 8))
contour = plt.contour(X, Y, Z, levels=20, cmap='viridis')
plt.clabel(contour, inline=True, fontsize=8)

# 軌跡のプロット
trajectory = np.array(trajectory)
plt.plot(trajectory[:, 0], trajectory[:, 1], 'ro-', label='Sophia Path')

# 矢印を追加して更新ベクトルを示す
for i in range(0, len(trajectory)-1, 10):  # 間引いて表示
    plt.arrow(trajectory[i, 0], trajectory[i, 1],
              trajectory[i+1, 0] - trajectory[i, 0],
              trajectory[i+1, 1] - trajectory[i, 1],
              head_width=0.3, head_length=0.3, fc='k', ec='k')

# 始点と終点をマーク
plt.plot(x_start, y_start, 'go', markersize=10, label='Start')
plt.plot(trajectory[-1, 0], trajectory[-1, 1], 'mo', markersize=10, label='End')

plt.title('Sophia Optimizer Behavior')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

Sophiaのコーディング例（PyTorch）：

# Sophia-H オプティマイザ
class SophiaH(torch.optim.Optimizer):
    def __init__(self, params, lr=1e-3, betas=(0.9, 0.999), rho=0.05, weight_decay=0.01, *, maximize=False):
        if not 0.0 <= lr:
            raise ValueError("Invalid learning rate: {}".format(lr))
        if not 0.0 <= betas[0] < 1.0:
            raise ValueError("Invalid beta parameter at index 0: {}".format(betas[0]))
        if not 0.0 <= betas[1] < 1.0:
            raise ValueError("Invalid beta parameter at index 1: {}".format(betas[1]))
        if not 0.0 <= rho:
            raise ValueError("Invalid rho parameter at index 1: {}".format(rho))
        defaults = dict(lr=lr, betas=betas, rho=rho, weight_decay=weight_decay, maximize=maximize)
        super(SophiaH, self).__init__(params, defaults)

    @torch.no_grad()
    def step(self, closure=None):
        loss = None
        if closure is not None:
            with torch.enable_grad():
                loss = closure()

        for group in self.param_groups:
            params_with_grad = []
            grads = []
            exp_avgs = []
            exp_avg_sqs = []
            state_sums = []
            max_exp_avg_sqs = []
            state_steps = []
            beta1, beta2 = group['betas']

            for p in group['params']:
                if p.grad is not None:
                    params_with_grad.append(p)
                    if p.grad.is_sparse:
                        raise RuntimeError('Adam does not support sparse gradients, please consider SparseAdam instead')
                    grads.append(p.grad)

                    state = self.state[p]

                    # State initialization
                    if len(state) == 0:
                        state['step'] = 0
                        # Exponential moving average of gradient values
                        state['exp_avg'] = torch.zeros_like(p, memory_format=torch.preserve_format)
                        # Exponential moving average of squared gradient values
                        state['exp_avg_sq'] = torch.zeros_like(p, memory_format=torch.preserve_format)

                    exp_avgs.append(state['exp_avg'])
                    exp_avg_sqs.append(state['exp_avg_sq'])

                    # update the steps for each param group update
                    state['step'] += 1
                    # record the step after step update
                    state_steps.append(state['step'])

            self.sophia(params_with_grad,
                   grads,
                   exp_avgs,
                   exp_avg_sqs,
                   state_steps,
                   beta1,
                   beta2,
                   group['rho'],
                   group['lr'],
                   group['weight_decay'],
                   group['maximize'])
        return loss

    def sophia(self, params,
                grads,
                exp_avgs,
                exp_avg_sqs,
                state_steps,
                beta1: float,
                beta2: float,
                rho: float,
                lr: float,
                weight_decay: float,
                maximize: bool):
        
        for i, param in enumerate(params):
            grad = grads[i]
            exp_avg = exp_avgs[i]
            exp_avg_sq = exp_avg_sqs[i]
            step = state_steps[i]

            bias_correction1 = 1 - beta1 ** step
            bias_correction2 = 1 - beta2 ** step

            if weight_decay != 0:
                grad = grad.add(param, alpha=weight_decay)

            # Decay the first and second moment running average coefficient
            exp_avg.mul_(beta1).add_(grad, alpha=1 - beta1)
            exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1 - beta2)
            
            # HUT
            h = exp_avg_sq
            h_clipped = torch.max(h, torch.full_like(h, rho))
            denom = (h_clipped/bias_correction2).sqrt().add_(1e-15)

            update = (exp_avg/bias_correction1).div(denom)

            if maximize:
                param.add_(update, alpha=lr)
            else:
                param.add_(update, alpha=-lr)

optimizer = SophiaH(
    net.parameters(),
    lr=1e-3,
    betas=(0.9, 0.999),
    rho=0.05,
    weight_decay=0.01
)

学習率の調整

コサインスケジューラー

学習率平滑化は、学習率をスムーズに変化させることで、学習の安定性を向上させる手法です。急激な学習率の変化を避け、モデルが損失関数の谷間を効果的に探索できるようにします。

数式

学習率平滑化は、一般的にコサインスケジューラーや線形スケジューラーで実現されます。

  • コサインスケジューラーは、ほとんどの最適化アルゴリズムで精度を向上させる傾向にあります。特に、SGD系やAdam系アルゴリズムで高い効果を発揮し、学習の安定性や収束速度を大幅に向上させます。ただし、タスクの特性やモデル設計に応じて効果が変動するため、適切なスケジューラーを選択することが重要です。
  • コサインスケジューラー

$$\alpha_t = \alpha_{\text{min}} + (\alpha_{\text{max}} – \alpha_{\text{min}}) \cdot \frac{1}{2} \left( 1 + \cos \left( \frac{t}{T} \pi \right) \right)$$

  • $α_t$：時刻 $t$ における学習率。
  • $\alpha_{\text{max}}, \alpha_{\text{min}}$：大・最小学習率。
  • $T$：スケジューラーの周期。

コーディング例_1（PyTorch ）：

  • 初期学習率の設定
    • 学習率の調整は、モデルの性能を最大限に引き出すために重要なステップです。コサインスケジューラーを使用する際でも、まず適切な初期学習率を学習率レンジテストを通して見つけることが成功の鍵となります。
    • 学習レンジテストとは？
      • 学習率レンジテストは、異なる学習率を試しながらモデルの損失関数の挙動を観察し、最適な学習率の範囲を特定する手法です。このテストを通じて、モデルが効果的に収束する学習率を見つけることができます。

初期学習の設定：

  • 損失の最小値に基づく方法(Min Loss)と損失の勾配に基づく方法(Gradient)の対数スケールでの平均(Averaged)を検討し、微調整を行う方法。
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
from scipy.signal import savgol_filter
from torch.optim.lr_scheduler import CosineAnnealingLR

# モデルと損失関数の準備
model = nn.Linear(10, 1)
criterion = nn.MSELoss()

# 学習率レンジテスト関数
def learning_rate_range_test(model, criterion, start_lr=1e-6, end_lr=10, num_iter=100, device="cpu"):
    model.to(device)
    optimizer = optim.SGD(model.parameters(), lr=start_lr)
    lrs = []
    losses = []
    
    lr = start_lr
    for i in range(num_iter):
        optimizer.param_groups[0]['lr'] = lr
        lrs.append(lr)
        
        inputs = torch.randn(32, 10).to(device)
        targets = torch.randn(32, 1).to(device)
        
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, targets)
        loss.backward()
        optimizer.step()
        
        losses.append(loss.item())
        
        lr = start_lr * (end_lr / start_lr) ** (i / num_iter)
    
    model.to("cpu")
    return lrs, losses

# 学習率レンジテストの実行
device = "mps" if torch.backends.mps.is_available() else "cpu"
lrs, losses = learning_rate_range_test(model, criterion, device=device)

# 損失の平滑化
window_length = 21
polyorder = 3
smoothed_losses = savgol_filter(losses, window_length, polyorder)

# 損失の勾配の計算
loss_gradients = np.gradient(smoothed_losses)

# プロットの作成
plt.figure(figsize=(12, 8))

# 損失のプロット
plt.subplot(2, 1, 1)
plt.plot(lrs, losses, label='Loss')
plt.plot(lrs, smoothed_losses, label='Smoothed Loss', linestyle='--')
plt.xscale('log')
plt.xlabel('Learning Rate')
plt.ylabel('Loss')
plt.title('Learning Rate Range Test')
plt.grid(True)
plt.legend()

# 損失の勾配のプロット
plt.subplot(2, 1, 2)
plt.plot(lrs, loss_gradients, label='Loss Gradient')
plt.xscale('log')
plt.xlabel('Learning Rate')
plt.ylabel('Loss Gradient')
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()

# 適切な初期学習率の決定 (損失の勾配が最も急な箇所)
max_grad_idx = np.argmax(loss_gradients)
optimal_lr_grad = lrs[max_grad_idx]

# 適切な初期学習率の決定 (損失が最小になる箇所)
min_loss_idx = np.argmin(losses)
optimal_lr_min = lrs[min_loss_idx]

# 対数スケールでの平均
optimal_lr = 10**((np.log10(optimal_lr_grad) + np.log10(optimal_lr_min)) / 2)

# 微調整 (例として、1/10にする)
optimal_lr = optimal_lr / 10

print(f"Optimal Learning Rate (Gradient): {optimal_lr_grad:.6f}")
print(f"Optimal Learning Rate (Min Loss): {optimal_lr_min:.6f}")
print(f"Optimal Learning Rate (Averaged): {optimal_lr:.6f}")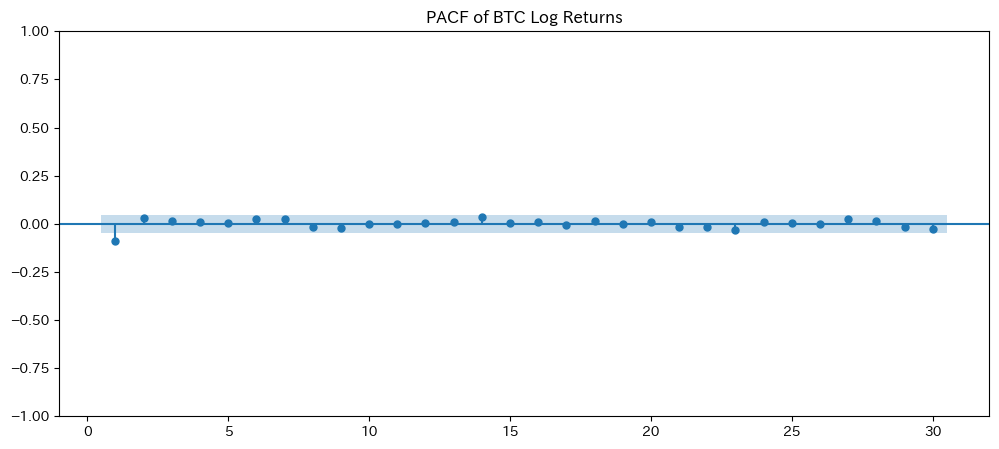
Optimal Learning Rate (Gradient): 7.244360
Optimal Learning Rate (Min Loss): 0.011482
Optimal Learning Rate (Averaged): 0.028840
  • 損失の最小値に基づく方法(Min Loss)と損失の勾配に基づく方法(Gradient)の対数スケールでの平均(Averaged)による微調整により、初期学習率は0.028840と算出。
  • 微調整の係数 (ここでは 1/10) は、データセットやモデルに応じて調整が必要な場合があります。
  • 学習率レンジテストのパラメータ (start_lr, end_lr, num_iter) や、平滑化のパラメータ (window_length, polyorder) も、データセットに応じて調整が必要な場合があります。

コサインスケジューラーの設定と適用（上記で算出した初期学習率を代入）

# コサインアニーリングスケジューラを用いた学習
model = nn.Linear(10, 1)
optimizer = optim.SGD(model.parameters(), lr=optimal_lr)
scheduler = CosineAnnealingLR(optimizer, T_max=50, eta_min=0.001)

lr_history = []
num_epochs = 100
for epoch in range(num_epochs):
    inputs = torch.randn(32, 10)
    targets = torch.randn(32, 1)
    
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    loss.backward()
    optimizer.step()
    
    scheduler.step()
    lr_history.append(scheduler.get_last_lr()[0])
    print(f"Epoch {epoch+1}, Learning Rate: {scheduler.get_last_lr()[0]:.6f}")

# 学習率の推移をプロット
plt.figure(figsize=(10, 6))
plt.plot(lr_history)
plt.title('Cosine Annealing Learning Rate Scheduler')
plt.xlabel('Epoch')
plt.ylabel('Learning Rate')
plt.grid(True)

# T_max ごとに縦線を追加
for i in range(num_epochs // 50):
    plt.axvline(x=(i + 1) * 50, color='r', linestyle='--')

plt.show()
Epoch 1, Learning Rate: 0.028813
Epoch 2, Learning Rate: 0.028731
Epoch 3, Learning Rate: 0.028594
…
Epoch 98, Learning Rate: 0.028731
Epoch 99, Learning Rate: 0.028813
Epoch 100, Learning Rate: 0.028840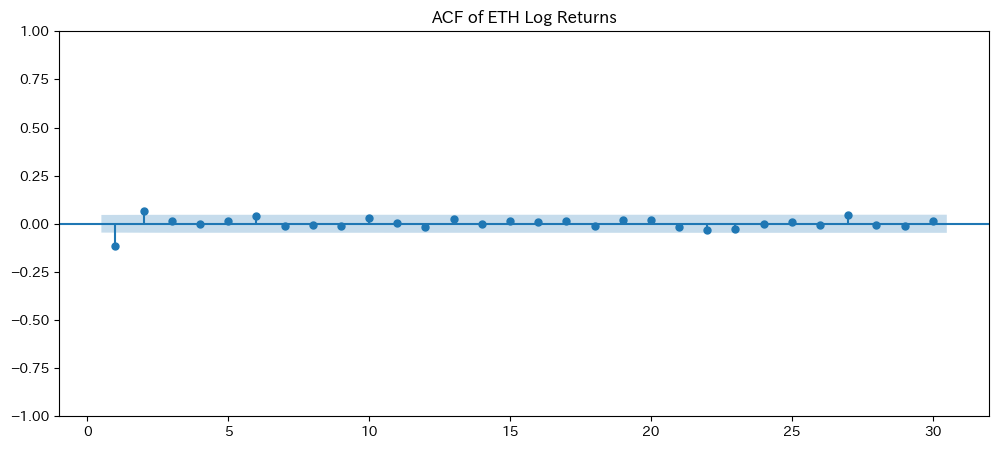

学習率は、T_maxエポックごとにコサインカーブに沿って初期値からeta_minまで減少し、再び初期値に戻ります。赤い破線はT_maxエポックの区切りを示しており、コサインアニーリングスケジューラの学習率調整を視覚的に示しています。

初期学習率の算出の仕方を選ぶ場合は、状況や目的に応じて判断する必要があります。

なぜコサインスケジューラーが効果的か？

  • 急激な変化を避ける
    • 学習率が滑らかに減少するため、学習が安定しやすく、最適化の終盤で微細な調整が可能。
  • 過学習を抑制
    • 終盤で学習率を低く保つため、過剰なフィッティングを防ぎ、汎化性能を向上。

どの最適化アルゴリズムで効果的か？

アルゴリズムカテゴリ効果が高い理由/特徴タスク例初期学習率の標準設定
Adam系 (Adam, AdamW, AdaBelief など)適応的な学習率によりスケジューリングの効果が反映されやすく、終盤の学習率調整が損失関数の谷間への収束を助ける。大規模言語モデル（BERT, GPT）や画像認識タスク。$1 \times 10^{-3}$
SGD系 (SGD, SGD with Momentum)固定学習率やシンプルなスケジューリングに依存しやすく、コサインスケジューラーの滑らかな調整が収束を安定化。モーメントとの併用で収束速度と最終性能が改善。ImageNetなどの大規模画像分類タスクやResNet系モデル。$1 \times 10^{-2}$
RAdam, Ranger, LookAhead初期段階の不安定性を軽減する機能を持ち、スケジューラーとの相性が良い。特にRangerは収束速度と汎化性能の両方で恩恵を受けやすい。分散トレーニングや大規模モデルの最適化タスク。$1 \times 10^{-3}$
LAMB, LARS大規模バッチトレーニング向けで固定学習率が前提。コサインスケジューラーの効果は限定的だが、特定のモデルで効果を発揮する場合もある。大規模分散トレーニング（例: BERTなどの言語モデル）。$1 \times 10^{-3}$
RMSProp収束速度を高める特性が強く、タスク依存でコサインスケジューラーの恩恵を受ける。複雑な損失関数を持つタスクでは安定性が向上することがある。リカレントニューラルネットワーク（RNN）や時間的データ解析タスク。$1 \times 10^{-3}$
Sophia効率的な2次情報の利用により、損失の高速収束と安定性を両立。大規模モデルや複雑なタスクで特に有効。BERTやGPTなどの大規模言語モデル、大規模画像認識タスク。$1 \times 10^{-3}$

効果が限定的なケースは？

  • 極小バッチサイズ
    • バッチサイズが極端に小さい場合、学習率調整の効果が勾配のノイズに埋もれる。
  • 短期間のトレーニング
    • トレーニング期間が短い場合、スケジューラーの効果が十分に発揮されない。

線形スケジューラー

線形スケジューラーは、学習率を一定の期間で線形に増加または減少させる手法です。ディープラーニングのトレーニングでは、初期段階で学習率を段階的に上昇させる「ウォームアップ」や、トレーニングの後半で徐々に減少させる用途でよく使用されます。

ウォームアップのための学習率増加

  • トレーニングの初期段階では、学習率を低く設定してから段階的に増加させ、モデルの安定性を向上させる。
  • 勾配が爆発しないようにしながら、適切な学習率へ到達させる。

学習の終盤での収束促進

  • トレーニングが進むにつれ、学習率を線形に減少させることで、損失関数の谷間をより正確に探索。

線形スケジューラーの数式

  • 線形スケジューラーは、学習率 $\alpha$ を以下のように調整します。
  • ウォームアップ (増加)

$$\alpha_t = \alpha_{\text{init}} + \frac{t}{T_{\text{warmup}}} (\alpha_{\text{max}} – \alpha_{\text{init}})$$

  • 線形減衰 (減少)

$$\alpha_t = \alpha_{\text{max}} \cdot \left( 1 – \frac{t – T_{\text{warmup}}}{T – T_{\text{warmup}}} \right)$$

記号説明
$\alpha_t$時刻 $t$ における学習率。
$\alpha_{init}$初期学習率。
$\alpha_{max}$最大学習率。
$T_{warmup}$ウォームアップ期間。
$T$総エポック数。
学習率の特徴トレーニングの終盤で学習率がゼロに近づく。

コーディング例_1（PyTorch ）：

初期学習の設定：

  • コサインスケジューラーの時と同様に、損失の最小値に基づく方法(Min Loss)と損失の勾配に基づく方法(Gradient)の対数スケールでの平均(Averaged)を検討し、微調整を行う方法を用います。
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
from scipy.signal import savgol_filter
from torch.optim.lr_scheduler import LinearLR

# モデルと損失関数の準備
model = nn.Linear(10, 1)
criterion = nn.MSELoss()

# 学習率レンジテスト関数
def learning_rate_range_test(model, criterion, start_lr=1e-6, end_lr=10, num_iter=100, device="cpu"):
    model.to(device)
    optimizer = optim.Adam(model.parameters(), lr=start_lr)
    lrs = []
    losses = []
    
    lr = start_lr
    for i in range(num_iter):
        optimizer.param_groups[0]['lr'] = lr
        lrs.append(lr)
        
        inputs = torch.randn(32, 10).to(device)
        targets = torch.randn(32, 1).to(device)
        
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, targets)
        loss.backward()
        optimizer.step()
        
        losses.append(loss.item())
        
        lr = start_lr * (end_lr / start_lr) ** (i / num_iter)
    
    model.to("cpu")
    return lrs, losses

# 学習率レンジテストの実行
device = "mps" if torch.backends.mps.is_available() else "cpu"
lrs, losses = learning_rate_range_test(model, criterion, device=device)

# 損失の平滑化
window_length = 21
polyorder = 3
smoothed_losses = savgol_filter(losses, window_length, polyorder)

# 損失の勾配の計算
loss_gradients = np.gradient(smoothed_losses)

# プロットの作成
plt.figure(figsize=(12, 8))

# 損失のプロット
plt.subplot(2, 1, 1)
plt.plot(lrs, losses, label='Loss')
plt.plot(lrs, smoothed_losses, label='Smoothed Loss', linestyle='--')
plt.xscale('log')
plt.xlabel('Learning Rate')
plt.ylabel('Loss')
plt.title('Learning Rate Range Test')
plt.grid(True)
plt.legend()

# 損失の勾配のプロット
plt.subplot(2, 1, 2)
plt.plot(lrs, loss_gradients, label='Loss Gradient')
plt.xscale('log')
plt.xlabel('Learning Rate')
plt.ylabel('Loss Gradient')
plt.grid(True)
plt.legend()

plt.tight_layout()
plt.show()

# 適切な初期学習率の決定 (損失の勾配が最も急な箇所)
max_grad_idx = np.argmax(loss_gradients)
optimal_lr_grad = lrs[max_grad_idx]

# 適切な初期学習率の決定 (損失が最小になる箇所)
min_loss_idx = np.argmin(losses)
optimal_lr_min = lrs[min_loss_idx]

# 対数スケールでの平均
optimal_lr = 10**((np.log10(optimal_lr_grad) + np.log10(optimal_lr_min)) / 2)

# 微調整 (例として、1/10にする)
optimal_lr = optimal_lr / 10

print(f"Optimal Learning Rate (Gradient): {optimal_lr_grad:.6f}")
print(f"Optimal Learning Rate (Min Loss): {optimal_lr_min:.6f}")
print(f"Optimal Learning Rate (Averaged): {optimal_lr:.6f}")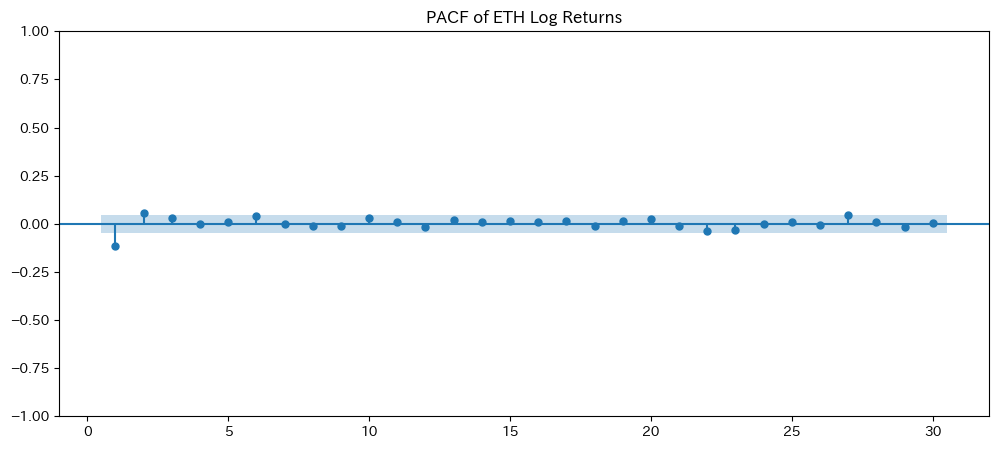
Optimal Learning Rate (Gradient): 7.244360
Optimal Learning Rate (Min Loss): 0.018621
Optimal Learning Rate (Averaged): 0.036728

線形スケジューラー（ウォームアップと線形減衰の組み合わせ）：

# ウォームアップと線形減衰を組み合わせた線形スケジューラ
model = nn.Linear(10, 1)
optimizer = optim.Adam(model.parameters(), lr=optimal_lr)

num_epochs = 100
warmup_steps = 20  # ウォームアップステップ数
total_steps = num_epochs # 総ステップ数

def lr_lambda(current_step):
    if current_step < warmup_steps:
        return float(current_step) / float(max(1, warmup_steps))
    else:
        return max(0.0, float(total_steps - current_step) / float(max(1, total_steps - warmup_steps)))

scheduler = LambdaLR(optimizer, lr_lambda=lr_lambda)

lr_history = []
for epoch in range(num_epochs):
    inputs = torch.randn(32, 10)
    targets = torch.randn(32, 1)
    
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    loss.backward()
    optimizer.step()
    
    scheduler.step()
    lr_history.append(scheduler.get_last_lr()[0])
    print(f"Epoch {epoch+1}, Learning Rate: {scheduler.get_last_lr()[0]:.6f}")

# 学習率の推移をプロット
plt.figure(figsize=(10, 6))
plt.plot(lr_history)
plt.title('Warmup and Linear Decay Learning Rate Scheduler')
plt.xlabel('Epoch')
plt.ylabel('Learning Rate')
plt.grid(True)
plt.show()
Epoch 1, Learning Rate: 0.001836
Epoch 2, Learning Rate: 0.003673
Epoch 3, Learning Rate: 0.005509
…
Epoch 98, Learning Rate: 0.000918
Epoch 99, Learning Rate: 0.000459
Epoch 100, Learning Rate: 0.000000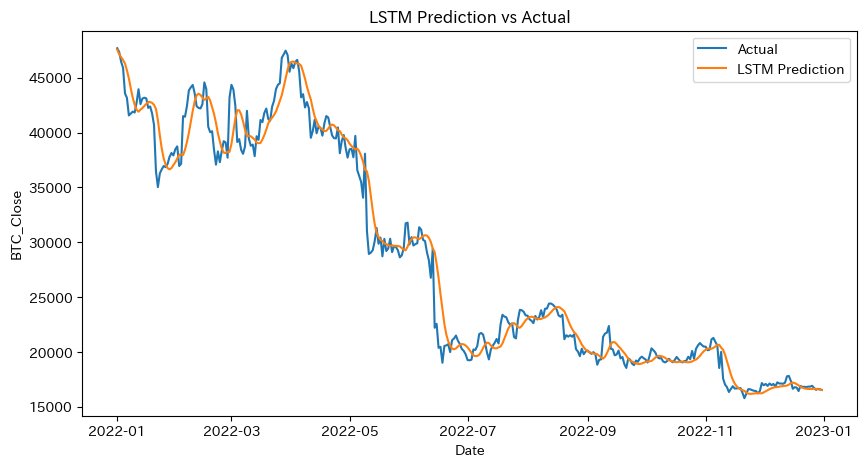
  • warmup_steps は、ウォームアップ期間のステップ数を指定します。データセットやモデルに応じて調整が必要な場合があります。
  • total_steps は、学習の総ステップ数を指定します。ここでは、エポック数と同じに設定しています。
  • 学習率レンジテストのパラメータ (start_lr, end_lr, num_iter) や、平滑化のパラメータ (window_length, polyorder) も、データセットに応じて調整が必要な場合があります。

なぜ線形スケジューラーが効果的か？

  • ウォームアップで学習の安定化
    • トレーニング初期の不安定な勾配を抑えるため、学習率を徐々に増加させ、モデルが安定して学習を始められるようにします。
  • 線形減衰で精密な収束
    • トレーニング後半では学習率を徐々に減少させ、損失関数の谷間（最適解付近）を細かく探索し、収束精度を高めます。
  • 広範なタスクで有効
    • 大規模言語モデル（BERT, GPT）や画像認識モデル（ResNet, EfficientNet）など、幅広いディープラーニングタスクで安定した性能向上を実現します。

どの最適化アルゴリズムで効果的か？

アルゴリズムカテゴリ効果が高い理由/特徴タスク例初期学習率の標準設定
Adam系 (Adam, AdamW, AdaBelief など)学習率の動的調整を活かし、ウォームアップで安定性、線形減衰で損失関数の谷間への精密な収束を助ける。大規模言語モデル（BERT, GPT）や画像認識タスク。$1 \times 10^{-3}$
SGD系 (SGD, SGD with Momentum)固定学習率を活用する特性があり、ウォームアップで勾配の安定性を確保、線形減衰で汎化性能を向上。ImageNetなどの大規模画像分類タスクやResNet系モデル。$1 \times 10^{-2}$
RAdam, Ranger, LookAhead初期段階の不安定性を抑制し、線形スケジューラーで収束速度と汎化性能が向上。Rangerは特に効果が大きい。大規模分散トレーニングや最適化タスク。$1 \times 10^{-3}$
LAMB, LARS大規模バッチトレーニングに特化し、ウォームアップが初期収束を助ける。線形減衰の効果は限定的。大規模分散トレーニング（例: GPT、BERTなどの言語モデル）。$1 \times 10^{-3}$
RMSPropリカレントタスクや複雑な損失関数の安定性を補強。ウォームアップで初期勾配を抑え、線形減衰で収束を加速。リカレントニューラルネットワーク（RNN）や時間的データ解析タスク。$1 \times 10^{-3}$
Sophia効率的な2次情報と線形スケジューラーの組み合わせで、特に大規模モデルの安定性と収束速度を両立。BERTやGPTなどの大規模言語モデル、大規模画像認識タスク。$1 \times 10^{-3}$

効果が限定的なケースは？

  • 短期間のトレーニング
    • 線形スケジューラーは長期的な学習率調整を目的としているため、エポック数が少ないタスクではウォームアップや減衰の効果が十分に発揮されません。
  • 極小バッチサイズ
    • バッチサイズが非常に小さい場合、勾配にノイズが多くなるため、学習率の変化が効果的に作用せず、モデルの収束が遅れることがあります。この場合、固定学習率や他のスケジューラー（例: ステップスケジューラー）が適する場合もあります。

データ拡張による汎化性能の向上

データ拡張とは？

データ拡張は、トレーニングデータを人工的に多様化させ、モデルの汎化性能を向上させる手法です。

データ拡張の目的

  • 過学習の防止
    • データセットのサイズを増やし、モデルが特定のパターンに過度に適合するのを防ぎます。
  • データの多様性
    • 実世界のデータに近づけるため、さまざまなバリエーションを導入します。これにより、モデルが見たことのないデータにも適応できるようになります。

画像の回転 (Rotation)

  • 画像をランダムな角度で回転させます。
  • 例：$-10^\circから+10^\circ$の範囲で回転。

効果：

  • 被写体の位置や姿勢の変化に対応する能力を向上させます。
  • 例：画像分類モデルが、傾いた文字や異なる視点の物体を正確に認識。

画像の各ピクセル座標 $(x, y)$ を角度 $θ$ だけ回転させる変換は次のように表されます。

$$\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}$$

$(x′,y′)$：回転後の座標。$θ$：回転角度（ラジアン単位）。

回転のコード例）

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
import torchvision.transforms.functional as TF

# 画像ファイルのパスを指定
original_image_path = 'pngファイルの画像パスを入力'

try:
    # 画像を開いて読み込み
    img = Image.open(original_image_path)
    img = img.convert('RGBA')  # PNG互換の形式に変換（必要に応じて）
    
    # 指定された角度での回転
    angles = [0, 90, 180, 270]
    rotated_images = [TF.rotate(img, angle) for angle in angles]

    # プロットを作成
    fig, axs = plt.subplots(1, len(angles), figsize=(15, 5))

    for ax, img, angle in zip(axs, rotated_images, angles):
        ax.imshow(img)
        ax.set_title(f"{angle}° Rotation")
        ax.axis('off')

    plt.tight_layout()
    plt.show()
except Exception as e:
    print(f"Error during processing: {e}")
  • transforms.functional.rotate を使用して指定された角度で画像を回転させています。

平行移動 (Translation)

  • 画像を上下左右に移動します。
  • 例：水平方向に±10ピクセル移動。

効果：

  • 被写体が異なる位置にある場合でも、モデルがその特徴を捉えられるようになります。
  • 例：被写体の位置が揺れるデータセット（顔検出、車両検出）。

平行移動は、各ピクセルの座標を固定量 $(t_x, t_y)$ だけ移動させる操作です。

$$\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
x + t_x \\
y + t_y
\end{pmatrix}$$

  • $t_x​,t_y​$：水平方向および垂直方向の移動距離。

平行移動のコード例）

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
import torchvision.transforms as transforms

# 画像ファイルのパスを指定
original_image_path = 'pngファイルの画像パスを入力'

try:
    # 画像を開いて読み込み
    img = Image.open(original_image_path)
    img = img.convert('RGBA')  # PNG互換の形式に変換（必要に応じて）
    
    # torchvision.transformsを使用してランダムに平行移動
    transform = transforms.RandomAffine(degrees=0, translate=(0.1, 0.1))
    
    # 平行移動画像を生成
    translated_images = [transform(img) for _ in range(2)]

    # プロットを作成
    fig, axs = plt.subplots(1, len(translated_images), figsize=(10, 5))

    for ax, img, i in zip(axs, translated_images, range(2)):
        ax.imshow(img)
        ax.set_title(f"Translation {i+1}")
        ax.axis('off')

    plt.tight_layout()
    plt.show()
except Exception as e:
    print(f"Error during processing: {e}")

transforms.RandomAffine を使用して画像をランダムに平行移動させています。

反転 (Flipping)

  • 画像を水平または垂直に反転します。
  • 例：水平反転は、左右を入れ替えた画像を生成。

効果：

  • 左右対称性が存在するデータ（例：動物、風景画像）で有効。
  • データの対称性に基づいてモデルの柔軟性を向上。

水平反転 (Horizontal Flip)

  • 画像の水平方向の反転は、座標の $x$軸を反転する操作で次のように表されます。

$$x′=W−1−x, y′=y$$

  • $W$：画像の幅。

垂直反転 (Vertical Flip)

  • 垂直方向の反転は、次のように表されます。

$$x′=x, y′=H−1−y$$

  • $H$：画像の高さ。

反転のコード例）

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
import torchvision.transforms as transforms

# 画像ファイルのパスを指定
original_image_path = 'pngファイルの画像パスを入力'

try:
    # 画像を開いて読み込み
    img = Image.open(original_image_path)
    img = img.convert('RGBA')  # PNG互換の形式に変換（必要に応じて）
    
    # torchvision.transformsを使用して水平反転と垂直反転
    horizontal_flip = transforms.RandomHorizontalFlip(p=1.0)  # 常に水平反転
    vertical_flip = transforms.RandomVerticalFlip(p=1.0)      # 常に垂直反転
    
    # 反転画像を生成
    flipped_images = [horizontal_flip(img), vertical_flip(img)]

    # プロットを作成
    fig, axs = plt.subplots(1, len(flipped_images), figsize=(10, 5))

    titles = ['Horizontal Flip', 'Vertical Flip']
    for ax, img, title in zip(axs, flipped_images, titles):
        ax.imshow(img)
        ax.set_title(title)
        ax.axis('off')

    plt.tight_layout()
    plt.show()
except Exception as e:
    print(f"Error during processing: {e}")

transforms.RandomHorizontalFlip と transforms.RandomVerticalFlip を使用して画像を水平反転および垂直反転させています。

ズーム (Scaling/Zooming)

  • 画像を拡大または縮小します。
  • 例：$80\%$から$100\%$のスケール範囲でランダムにリサイズ。

効果：

  • 被写体が異なる距離にある場合でも、重要な特徴を抽出する能力を向上。
  • 特に、顔認識や物体検出などで有効。

画像の拡大や縮小は、拡大率（スケール） $s$ を適用して座標を変換する操作です。

$$\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
s \cdot x \\
s \cdot y
\end{pmatrix}$$

$s>1$：画像を拡大。$0<s<1$：画像を縮小。

ズームのコード例）

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
import torchvision.transforms as transforms

# 画像ファイルのパスを指定
original_image_path = 'pngファイルの画像パスを入力'

try:
    # 画像を開いて読み込み
    img = Image.open(original_image_path)
    img = img.convert('RGBA')  # PNG互換の形式に変換（必要に応じて）
    
    # torchvision.transformsを使用してランダムにズーム
    transform = transforms.RandomResizedCrop(size=img.size[0], scale=(0.4, 0.6, 0.8, 1.0))
    
    # ズーム画像を生成
    zoomed_images = [transform(img) for _ in range(4)]

    # プロットを作成
    fig, axs = plt.subplots(1, len(zoomed_images), figsize=(10, 5))

    for ax, img, i in zip(axs, zoomed_images, range(4)):
        ax.imshow(img)
        ax.set_title(f"Zoom {i+1}")
        ax.axis('off')

    plt.tight_layout()
    plt.show()
except Exception as e:
    print(f"Error during processing: {e}")

transforms.RandomResizedCrop を使用して画像をランダムにズームしています。

色調変化 (Color Jittering)

  • 画像の明るさ、コントラスト、彩度、色相をランダムに変更。
  • 例: 明るさを$±10\%$、コントラストを$±20\%$調整。

効果：

  • 照明条件や環境が異なるデータに対するロバスト性を向上。
  • 例：屋内と屋外での物体認識。

明るさの調整 (Brightness)

  • 明るさの調整は、各ピクセル値 $I(x, y)$ に定数 $b$ を加算する操作です。

$$I'(x, y) = I(x, y) + b$$

$b>0$：画像を明るく。$b<0$：画像を暗く。

コントラストの調整 (Contrast)

  • コントラストの調整は、ピクセル値の平均値 $\mu$ に対してスケール $c$ を適用します。

$$I'(x, y) = \mu + c \cdot (I(x, y) – \mu)$$

$c>1$：コントラストを増加。$0<c<1$：コントラストを減少。

彩度の調整 (Saturation)

  • 彩度の調整は、各ピクセルの色成分 (R,G,B)(R, G, B)(R,G,B) にスケール $s$ を適用します。

$$R’ = R \cdot s, \quad G’ = G \cdot s, \quad B’ = B \cdot s$$

$s>1$：彩度を増加。$0<s<1$：彩度を減少。

色調変化のコード例）

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
import torchvision.transforms as transforms

# 画像ファイルのパスを指定
original_image_path = 'pngファイルの画像パスを入力'

try:
    # 画像を開いて読み込み
    img = Image.open(original_image_path)
    img = img.convert('RGBA')  # PNG互換の形式に変換（必要に応じて）
    
    # torchvision.transformsを使用して色調変化
    transform = transforms.ColorJitter(brightness=0.3, contrast=0.3, saturation=0.2, hue=0.1)
    
    # 色調変化画像を生成
    jittered_images = [transform(img) for _ in range(4)]

    # プロットを作成
    fig, axs = plt.subplots(1, len(jittered_images), figsize=(15, 5))

    for ax, img, i in zip(axs, jittered_images, range(4)):
        ax.imshow(img)
        ax.set_title(f"Color Jitter {i+1}")
        ax.axis('off')

    plt.tight_layout()
    plt.show()
except Exception as e:
    print(f"Error during processing: {e}")

transforms.ColorJitter を使用して画像の明るさ、コントラスト、彩度、色相をランダムに調整しています。

切り抜き (Cropping)

  • 画像の一部をランダムに切り抜いて再スケール。
  • 例：ランダムに中央部分を拡大して切り抜く。

効果：

  • 被写体の一部が欠損していても認識可能なモデルを作成。
  • 特に、部分的に遮蔽された物体認識タスクで有効。

画像の一部を $x_0, y_0$​ を左上座標として切り抜き、幅 $w$、高さ $h$ を得る操作です。

$$I'(x, y) = I(x + x_0, y + y_0), \quad 0 \leq x < w, \quad 0 \leq y < h$$

切り抜きのコード例）

import matplotlib.pyplot as plt
import numpy as np
from PIL import Image
import torchvision.transforms as transforms

# 画像ファイルのパスを指定
original_image_path = 'pngファイルの画像パスを入力'

try:
    # 画像を開いて読み込み
    img = Image.open(original_image_path)
    img = img.convert('RGBA')  # PNG互換の形式に変換（必要に応じて）
    
    # torchvision.transformsを使用してランダムに切り抜き
    transform = transforms.Compose([
        transforms.RandomCrop(size=(28, 28)),
        transforms.Resize(img.size)  # 元のサイズにリサイズ
    ])
    
    # 切り抜き画像を生成
    cropped_images = [transform(img) for _ in range(4)]

    # プロットを作成
    fig, axs = plt.subplots(1, len(cropped_images), figsize=(15, 5))

    for ax, img, i in zip(axs, cropped_images, range(4)):
        ax.imshow(img)
        ax.set_title(f"Crop {i+1}")
        ax.axis('off')

    plt.tight_layout()
    plt.show()
except Exception as e:
    print(f"Error during processing: {e}")

画像がぼやける原因は、transforms.RandomCrop が画像を指定されたサイズ（ここでは28×28）に切り抜くためです。これにより、元の画像が小さくなり、プロット時に拡大されるため、ぼやけて見えることがあります。

このコードでは、transforms.RandomCrop を使用してランダムに切り抜いた後、元のサイズにリサイズしてプロットすることで、ぼやけを軽減します。

CIFAR-10データセットを使ったデータ拡張の実装）

  • CIFAR-10データセットとは？
    • 機械学習とコンピュータビジョンの分野で広く使用される画像データセットです。
    • CIFAR-10データセットは、10種類のクラスに分類された60,000枚のカラー画像で構成されています。
    • 各クラスには6,000枚の画像が含まれています。
    • 10種類のクラス内容
      • 飛行機 (airplane)
      • 自動車 (automobile)
      • 鳥 (bird)
      • 猫 (cat)
      • 鹿 (deer)
      • 犬 (dog)
      • カエル (frog)
      • 馬 (horse)
      • 船 (ship)
      • トラック (truck)
import torch
import torchvision.transforms as transforms
import torchvision.datasets as datasets
import matplotlib.pyplot as plt
import numpy as np

# Apple SiliconのGPUを使用するためのデバイス設定
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
print(f"Using device: {device}")

# データ拡張の定義
transform = transforms.Compose([
    transforms.RandomHorizontalFlip(),
    transforms.RandomVerticalFlip(),
    transforms.RandomResizedCrop(size=32, scale=(0.8, 1.0)),
    transforms.ColorJitter(brightness=0.2, contrast=0.2, saturation=0.2, hue=0.1),
    # transforms.RandomCrop(size=(28, 28)),
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))
])

# データセットの定義（例としてCIFAR-10を使用）
train_dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=5, shuffle=True)

# サンプルデータの取得
data_iter = iter(train_loader)
images, labels = next(data_iter)

# デバイスに転送
images = images.to(device)
labels = labels.to(device)

# 拡張された画像を表示
fig, axes = plt.subplots(1, 5, figsize=(12, 2))
for idx in range(5):
    img = images[idx].cpu().numpy().transpose((1, 2, 0))
    img = np.clip(img * 0.5 + 0.5, 0, 1)  # 正規化を戻す
    axes[idx].imshow(img)
    axes[idx].axis('off')
plt.show()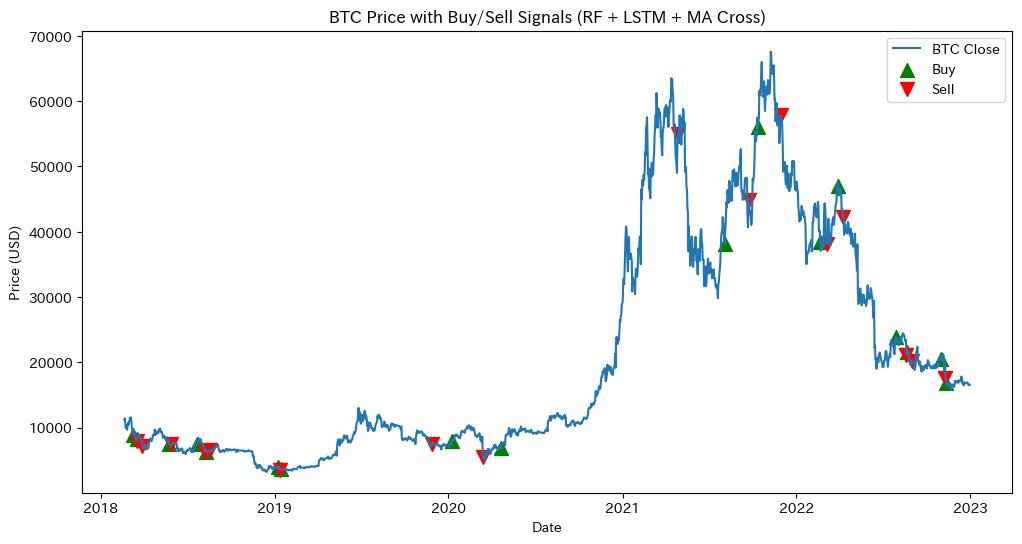

正則化手法による汎化性能の向上

正則化の必要性

  • ディープラーニングモデルは高い表現力を持つため、トレーニングデータに過度に適合（過学習）しやすい。
  • 過学習とは？
    • トレーニングデータでは高い精度を示すが、テストデータでは性能が低下すること。

正則化の目的

  • モデルの複雑さを抑えることで、汎化性能を向上。
  • 過剰適合を防ぎ、未知のデータに対する予測性能を高める。

L２正則化

L2正則化（別名ウェイトデケイ）は、過学習を防ぐためにモデルの重みの大きさを抑制する手法です。モデルの複雑さを抑制し、過学習を防止しています。

このアルゴリズムは【第5回】モデル評価と最適化（後編）でL1正則化とともに説明していますが、今回はニューラルネットワークでPyTorchを使った実装を紹介しておきます。復習として下記URLを確認しておいてください。

【第5回】モデル評価と最適化（後編）
目的 このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用...
shion.blog
2024.10.27

L2正則化はすべての特徴量を使用しつつ重みを抑えることで、モデルの汎化能力を狙い、特徴量を外すことなく過学習を抑えます。

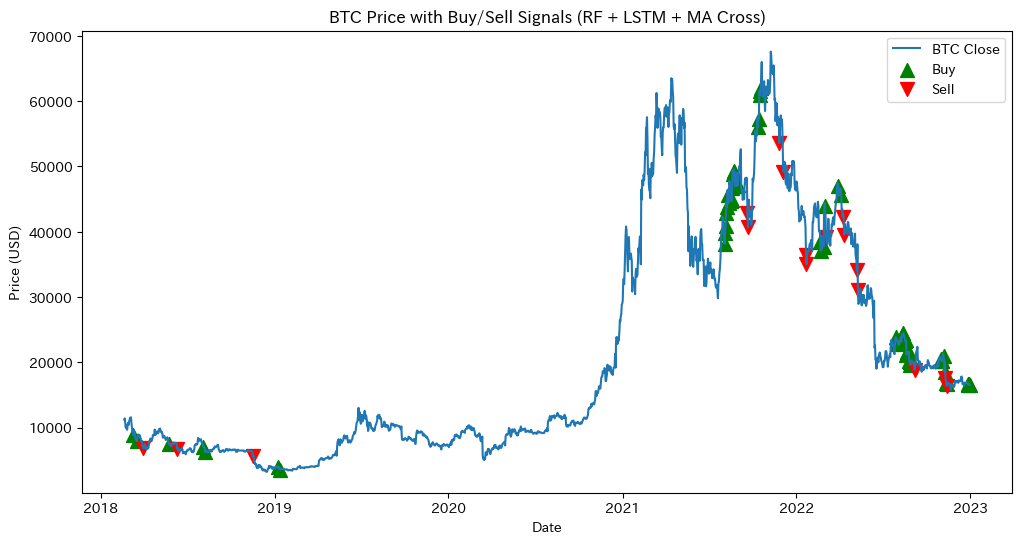
L2正則化（PyTorch）：

import torch.optim as optim

# オプティマイザの設定（L2正則化を適用）
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=0.0005)

L1正則化（PyTorch）：

L1正則化は、モデルの重みの絶対値の合計を損失関数に追加することで、過学習を防ぐ手法です。PyTorchでは、L1正則化を直接オプティマイザに設定することはできませんが、カスタム損失関数を定義することで実装できます。

L1正則化は最終的に特徴量の重みが0に近づくため、特徴量の選択がしやすくなります。


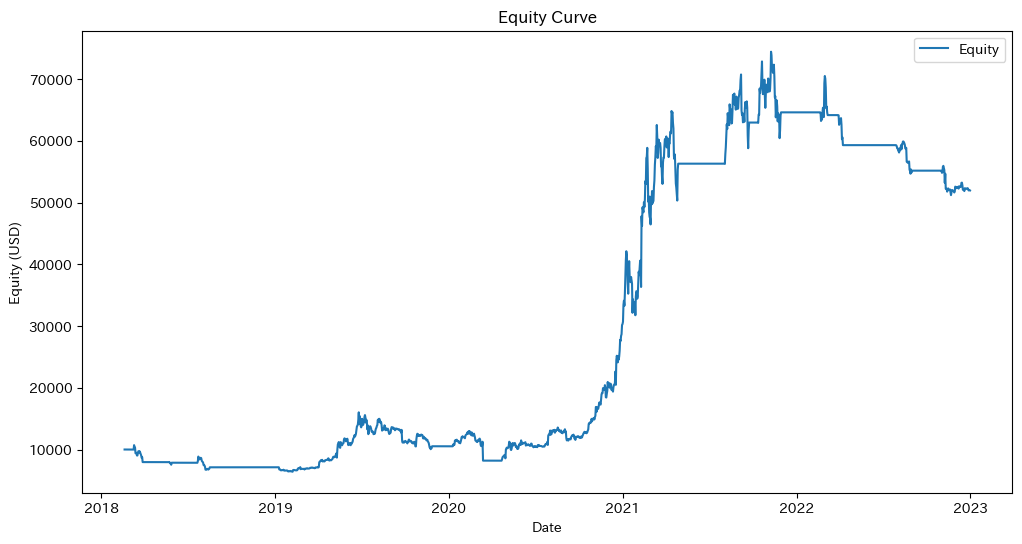
# オプティマイザの設定
optimizer = optim.SGD(model.parameters(), lr=0.01)

# カスタム損失関数（L1正則化を含む）
def l1_regularization(model, lambda_l1):
    l1_norm = sum(p.abs().sum() for p in model.parameters())
    return lambda_l1 * l1_norm

# トレーニングループ
def train(model, device, train_loader, optimizer, epoch, lambda_l1):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = nn.CrossEntropyLoss()(output, target)
        loss += l1_regularization(model, lambda_l1)  # L1正則化を追加
        loss.backward()
        optimizer.step()
        if batch_idx % 100 == 0:
            print(f'Train Epoch: {epoch} [{batch_idx * len(data)}/{len(train_loader.dataset)} ({100. * batch_idx / len(train_loader):.0f}%)]\tLoss: {loss.item():.6f}')

Elastic Net（PyTorch）：

Elastic Netは、L1正則化とL2正則化を組み合わせた正則化手法です。これにより、L1正則化のスパース性とL2正則化のリッジ回帰の特性を同時に持つことができます。PyTorchを使用してElastic Netを実装するには、カスタム損失関数を定義し、L1正則化とL2正則化の両方を含める必要があります。

# オプティマイザの設定
optimizer = optim.SGD(model.parameters(), lr=0.01)

# カスタム損失関数（Elastic Net正則化を含む）
def elastic_net_regularization(model, lambda_l1, lambda_l2):
    l1_norm = sum(p.abs().sum() for p in model.parameters())
    l2_norm = sum(p.pow(2).sum() for p in model.parameters())
    return lambda_l1 * l1_norm + lambda_l2 * l2_norm

# トレーニングループ
def train(model, device, train_loader, optimizer, epoch, lambda_l1, lambda_l2):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = nn.CrossEntropyLoss()(output, target)
        loss += elastic_net_regularization(model, lambda_l1, lambda_l2)  # Elastic Net正則化を追加
        loss.backward()
        optimizer.step()
        if batch_idx % 100 == 0:
            print(f'Train Epoch: {epoch} [{batch_idx * len(data)}/{len(train_loader.dataset)} ({100. * batch_idx / len(train_loader):.0f}%)]\tLoss: {loss.item():.6f}')

ドロップアウト

ドロップアウトは、トレーニング中に一部のニューロンをランダムに無効化（0に設定）する手法で、ニューロン間の相互依存を減少させ、より一般化された特徴表現を学習します。この手法も【第5回】モデル評価と最適化（後編）で詳しく説明していますので確認してみて下さい。

【第5回】モデル評価と最適化（後編）
目的 このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用...
shion.blog
2024.10.27

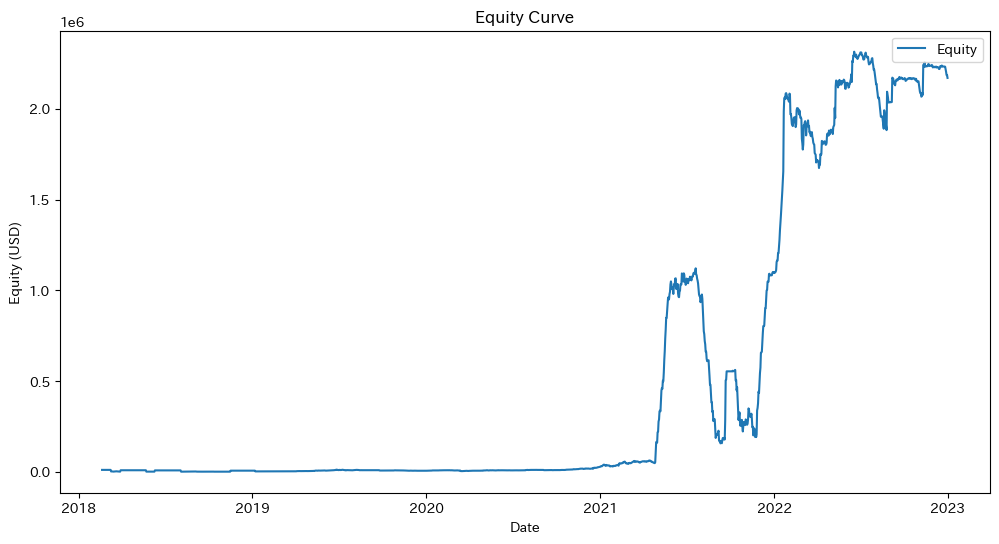
ドロップアウトの利点と欠点：

利点：

利点詳細
過学習の防止ニューロンをランダムに無効化することで、特定のニューロンに依存しすぎるのを防ぐ。
汎化性能の向上トレーニング中に多様なサブネットワークを学習し、未知のデータへの適応力が向上。

欠点：

欠点詳細
トレーニング時間増加ニューロンを無効化することで収束までにより多くのエポックが必要。
一部タスクで非効率RNNや時系列タスクでは、他の正則化手法（例: 勾配クリッピング）が有効な場合がある。

ドロップアウトと他の正則化手法の比較

正則化手法特徴ドロップアウトとの関係
L2正則化重みの大きさを直接制御。ドロップアウトと組み合わせることでさらなる性能向上が可能。
バッチ正規化各バッチ内でのデータ分布を調整し、学習の安定性を向上。ドロップアウトと併用する場合、効果が打ち消されることもある。

ドロップアウト（PyTorch）：

ドロップアウトを含むニューラルネットワークモデルの定義

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# 通常のドロップアウトを含むニューラルネットワークモデルの定義
class DropoutModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout_rate=0.5):
        super(DropoutModel, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.dropout = nn.Dropout(p=dropout_rate)  # 通常のドロップアウト層
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.dropout(x)  # 通常のドロップアウトを適用
        x = self.fc2(x)
        return x

# モデルのインスタンス化
model = DropoutModel(input_dim=256, hidden_dim=128, output_dim=10)

# 損失関数とオプティマイザ
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# ダミーデータ
inputs = torch.randn(32, 256)  # バッチサイズ32, 入力次元256
targets = torch.randint(0, 10, (32,))  # 10クラス分類

# トレーニングループ
for epoch in range(5):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    loss.backward()
    optimizer.step()

    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")
Epoch 1, Loss: 2.3080
Epoch 2, Loss: 2.2948
Epoch 3, Loss: 2.1137
Epoch 4, Loss: 2.0096
Epoch 5, Loss: 1.7940

シンプルな構造のニューラルネットワークにはドロップアウトが有効です。

様々なドロップアウトの手法

SpatialDropout

SpatialDropoutは、従来のドロップアウト（Dropout）を拡張した手法で、CNN（畳み込みニューラルネットワーク）に特化した正則化技術です。
従来のドロップアウトでは、各ニューロン（スカラー値）をランダムに無効化しますが、SpatialDropoutでは特徴マップ全体（チャンネル単位）を無効化します。

動作原理

  • SpatialDropoutの主な特徴は、畳み込み層の出力である特徴マップ内の空間的な連続性を保つ点です。

数式：

各チャンネル全体を無効化するため、ある特徴マップの出力を $X \in \mathbb{R}^{C \times H \times W}$ とすると、SpatialDropoutの動作は次のように定義されます。

$$X'_c =
\begin{cases} 
X_c & \text{with probability } 1 - p, \\
0 & \text{with probability } p.
\end{cases}$$
  • $X_c$​：チャンネル $c$ の特徴マップ。
  • $p$：ドロップアウト率（無効化するチャンネルの確率）。
  • $X’_c$​：SpatialDropout後のチャンネル $c$ の出力。

$$X’ = X \odot M$$

  • $M∈{0,1}^C: Bernoulli$分布に従うランダムマスク（チャンネルごとに生成）。
  • $\odot$：要素ごとの積。

特徴：

  • 空間的な連続性（各チャンネル内の $H×W$ ピクセル）は維持。
  • チャンネルごとの無効化により、CNNが過剰に特定の特徴マップに依存することを防止。

SpatialDropoutの効果と利点

項目内容
過学習防止特徴マップ全体を無効化することで、特定の特徴マップへの依存を減少。
空間的な連続性の保持ピクセル単位で無効化する従来のドロップアウトとは異なり、空間的な情報を失わない。
汎化性能の向上特徴マップごとの冗長性を排除し、モデルの未知データへの適応力を向上。

SpatialDropout（PyTorch）：

CNNでSpatialDropoutを使って定義を行います。

import torch.nn as nn

# CNNモデルの定義
class CNNModel(nn.Module):
    def __init__(self):
        super(CNNModel, self).__init__()
        self.conv1 = nn.Conv2d(3, 64, kernel_size=3, padding=1)  # 入力チャンネル3, 出力チャンネル64
        self.dropout = nn.Dropout2d(p=0.5)  # SpatialDropoutの適用
        self.conv2 = nn.Conv2d(64, 128, kernel_size=3, padding=1)
        self.fc1 = nn.Linear(128 * 32 * 32, 256)
        self.fc2 = nn.Linear(256, 10)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = self.dropout(x)  # チャンネル単位でドロップアウト
        x = F.relu(self.conv2(x))
        x = x.view(x.size(0), -1)  # フラット化
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

トレーニングループ

# モデル定義
model = CNNModel()

# 損失関数とオプティマイザ
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# ダミーデータでのトレーニング例
inputs = torch.randn(16, 3, 32, 32)  # バッチサイズ16, 入力チャンネル3, 高さ32, 幅32
targets = torch.randint(0, 10, (16,))  # 10クラス分類タスク

# トレーニングステップ
for epoch in range(5):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    loss.backward()
    optimizer.step()
    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")

モデルの実装

import matplotlib.pyplot as plt
import numpy as np

# サンプルデータ
sample_input = torch.randn(1, 3, 32, 32)  # 1画像、3チャンネル

# ドロップアウト適用前後の出力
model = CNNModel()
with torch.no_grad():
    before_dropout = model.conv1(sample_input)
    after_dropout = model.dropout(before_dropout)

# 特徴マップの可視化（1チャンネル目を表示）
def visualize_feature_map(feature_map, title):
    feature_map = feature_map.squeeze(0)[0].numpy()  # チャンネル1を取得
    plt.imshow(feature_map, cmap='viridis')
    plt.title(title)
    plt.axis('off')
    plt.show()

visualize_feature_map(before_dropout, "Before SpatialDropout")
visualize_feature_map(after_dropout, "After SpatialDropout")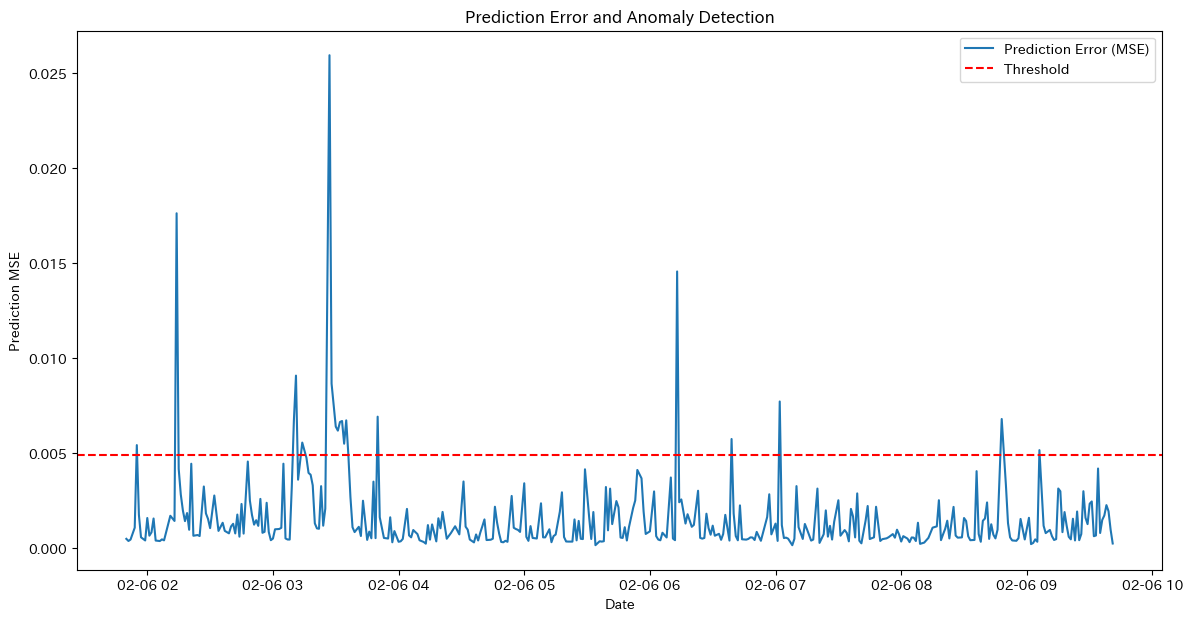

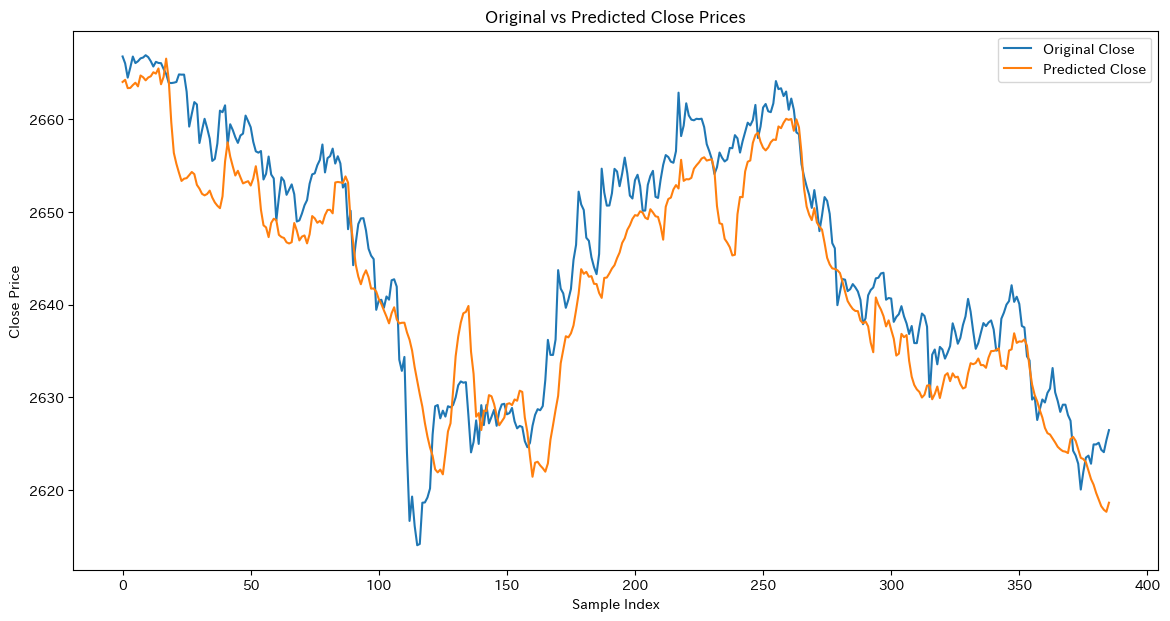
このコードは、SpatialDropout を適用する前後の特徴マップを可視化することで、SpatialDropout の効果を視覚的に確認するものです。SpatialDropout を適用することで、特定のチャンネル全体が無効化され、モデルが特定のチャンネルに過度に依存することを防ぎ、過学習を防ぐ効果があります。

Variational Dropout（変分ドロップアウト）

Variational Dropoutは、従来の固定値ドロップアウトを拡張し、ドロップアウト率をパラメータとして学習可能にする手法です。この手法では、各ニューロンごとに無効化確率を動的に調整し、タスクに応じて効率的に不要なニューロンを除去します。ドロップアウトに比べ高度なモデルや大規模なデータセットに対して効果的です。

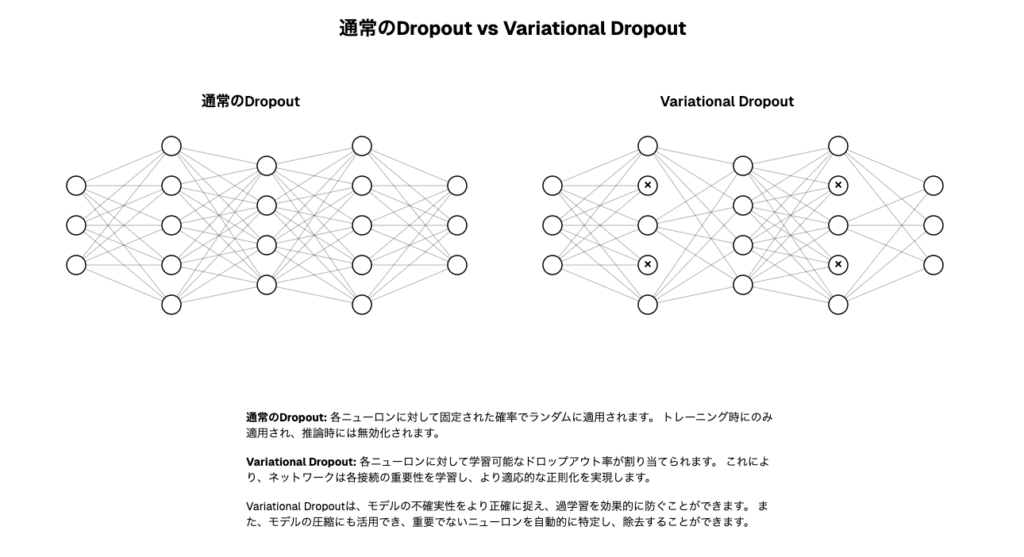
動作原理

数式：Variational Dropoutは、確率的モデルを基盤としています。

  • ドロップアウト率の定義：
    • ドロップアウトの確率 $\pi_i$​ をニューロン $i$ に対するパラメータとして定義します。

$$π_i = σ_{(z_i)}$$

  • $z_i$​：ニューロン $i$ の学習可能なパラメータ。
  • $σ$：シグモイド関数（確率値を0から1の範囲にスケーリング）。
  • マスク生成：
    • 各ニューロンに対してベルヌーイ分布に基づくマスク $m_i$​ を生成します。

$$m_i \sim \text{Bernoulli}(1 – \pi_i)$$

  • $m_i$​=0: 無効化されたニューロン。
  • $m_i$​=1: 有効なニューロン。
  • ドロップアウト後の出力：
    • ニューロンの出力 $x_i’$​ は次のように計算されます。

$$x’_i=m_i⋅x_i$$
​

  • $x_i$：ドロップアウト前のニューロンの出力。
  • 再スケール：
    • ドロップアウト後の値をスケール補正して、出力の期待値を一定に保ちます。

$$x’_i = \frac{m_i \cdot x_i}{1 – \pi_i}$$

学習可能性

  • ドロップアウト率 $\pi_i$​ は、他のモデルパラメータと同様に勾配降下法を用いて学習されます。この特性により、特定のニューロンを動的に「重要でない」と判断し、効率的なモデルを構築できます。

Variational Dropoutの利点と応用

利点：

利点説明
学習可能なドロップアウト率各ニューロンに最適な無効化確率を動的に調整。
不要なニューロンの除去ニューロンの重要度に基づいてモデルを簡素化。
汎化性能の向上過学習防止と効率的な特徴抽出を実現。

欠点：

欠点説明
計算コストの増加各ニューロンのドロップアウト率を学習するため、計算負荷が高くなる。
実装の複雑性通常のドロップアウトよりも高度な実装が必要であり、初心者には扱いづらい場合がある。
収束の遅延学習可能なドロップアウト率の最適化により、収束までに時間がかかることがある。

適用例：

  • モデルが複雑で、通常のドロップアウトでは十分な正則化が得られない場合に効果的。
  • 各重みに対して異なるドロップアウト率を適用することで、より細かい制御が可能。
  • 高度なモデルや大規模なデータセットに対して効果的。

用途：

  • 自然言語処理（NLP）；RNNやTransformerモデルで有効。
  • ベイズニューラルネットワーク：不確実性推定に利用可能。

Variational Dropout（PyTorch）：

Variational Dropoutを適用するための定義

import torch
import torch.nn as nn
import torch.nn.functional as F

# Variational Dropoutを含むニューラルネットワークモデルの定義
class VariationalDropout(nn.Module):
    def __init__(self, input_dim, initial_dropout_rate=0.5):
        super(VariationalDropout, self).__init__()
        self.logit_dropout_rate = nn.Parameter(torch.full((input_dim,), initial_dropout_rate))
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        # ドロップアウト率をシグモイド関数でスケーリング
        dropout_rate = self.sigmoid(self.logit_dropout_rate)
        
        # Bernoulli分布に基づいてマスクを生成
        mask = torch.bernoulli(1 - dropout_rate).to(x.device)
        
        # 出力のスケーリング補正
        output = x * mask / (1 - dropout_rate + 1e-8)  # 1e-8でゼロ割りを防止
        return output

Variational Dropoutを適用したモデルを定義

class VariationalModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, initial_dropout_rate=0.5):
        super(VariationalModel, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.variational_dropout = VariationalDropout(hidden_dim, initial_dropout_rate)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.variational_dropout(x)  # Variational Dropoutを適用
        x = self.fc2(x)
        return x

トレーニングループ

import torch.optim as optim

# モデルのインスタンス化
model = VariationalModel(input_dim=256, hidden_dim=128, output_dim=10)

# 損失関数とオプティマイザ
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# ダミーデータ
inputs = torch.randn(32, 256)  # バッチサイズ32, 入力次元256
targets = torch.randint(0, 10, (32,))  # 10クラス分類

# トレーニングループ
for epoch in range(5):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    loss.backward()
    optimizer.step()

    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")
Epoch 1, Loss: 2.4494
Epoch 2, Loss: 2.2814
Epoch 3, Loss: 2.2337
Epoch 4, Loss: 2.1980
Epoch 5, Loss: 1.9698

Variational Dropoutは、各重みに対して異なるドロップアウト率を適用することで、より柔軟な正則化を実現します。複雑なモデルや大規模なデータセットに対して効果的です。今回の様なシンプルな構造のニューラルネットワークの場合は通常のドロップアウトの方が適していると言えます。

DropConnect

DropConnectは、従来のドロップアウト（Dropout）がニューロンの出力を無効化するのに対して、重み（接続）を無効化する手法です。言い換えるとドロップコネクトではノードを不活性化させるのではなく、代わりにノード間の結合をランダムに切ります。
これにより、重みのスパース性を高め、モデルが特定の重みに依存するのを防ぎます。

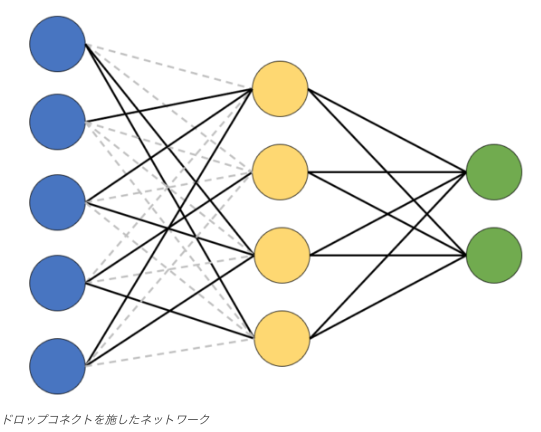
https://zero2one.jp/learningblog/drop-outs-and-drop-connections/?srsltid=AfmBOopawx-vbj0PkQh-1l1PhOzeLH10h4QNo9rrhaXCn4vBc3BdSqPP

動作原理

数式：

  • 重みマスクの生成
    • 各重みに対して、無効化確率 $p$ に基づきBernoulli分布からマスク $m_{ij}$​ を生成します。

$$m_{ij} \sim \text{Bernoulli}(1 – p)$$

  • $m_{ij}$​：重み $w_{ij}$​ に対応するマスク（0または1）。
  • $p$：無効化の確率。
  • 重みのスパース化
    • マスクを重みに適用し、DropConnect後の重み $\tilde{w}_{ij}$ を計算します。
  • 再スケール（期待値の補正）
    • ドロップアウトと同様に、トレーニング中に無効化された重みがあるため、スケール補正を行い出力の期待値を一定に保ちます。

$$\widetilde{w}_{ij} = \frac{m_{ij} \cdot w_{ij}}{1 – p}$$

  • 出力の計算
    • ドロップ接続後の出力 $y_i$ は以下で定義されます。

$$y_i = \sigma \left( \sum_{j} \widetilde{w}_{ij} x_{j} + b_{i} \right)$$

$x_j$：入力値。$σ$：活性化関数。$b_i​$：バイアス項。

DropConnectの利点と欠点

利点：

利点説明
重みのスパース性重みを無効化することで、モデルが特定の重みに依存するのを防ぎます。
汎化性能の向上過学習を抑制し、未知のデータに対する適応能力を向上させます。
CNNや全結合層での有効性高次元データや複雑なモデルで特に効果を発揮し、優れたパフォーマンスを実現します。

欠点：

欠点説明
計算コストの増加重みごとにマスクを生成するため、ドロップアウトよりも計算量が増加します。
実装の複雑さニューロン単位の無効化と比較して、実装が複雑で初心者には扱いにくい場合があります。

適用例：

適用例説明
画像分類高次元の特徴マップを扱うCNNで、スパース性を高め、モデルの汎化性能を向上。
回帰タスク全結合層を含むタスクで、過学習を防ぎつつ精度を維持。
物体検出特定の特徴抽出器への過剰依存を防止し、モデルの安定性を向上。

論文：

Regularization of Neural Networks using DropConnect
We introduce DropConnect, a generalization of DropOut, for regularizing large fully-connected layers within neural netwo...
proceedings.mlr.press
  • DropConnectの新規性
    • DropConnectは、Dropoutを改良した新しい手法で、重み行列の一部をランダムに無効化します。この仕組みにより、トレーニング時にサンプルごとに異なる接続構造を作り出し、過学習を抑えつつ、より高い正則化効果を得られる点が特徴です。
  • 実験結果の優位性
    • DropConnectは、MNISTやCIFAR-10といったベンチマークデータセットで、Dropoutよりも優れた性能を発揮しました。特に、データ拡張や複数モデルを組み合わせるアンサンブル手法を併用することで、過学習を抑えながら最先端の精度を達成しています。
    • DropConnectは、深い層や広い層でDropoutより優れた性能を発揮します。また、重みマスクをランダムに適用することで多様なモデル表現を生み出し、過学習を抑えながらモデルの汎化性能を高める効果があります。

DropConnect（PyTorch）：

import torch
import torch.nn as nn
import torch.optim as optim

# DropConnectレイヤーの定義
class DropConnect(nn.Module):
    def __init__(self, p=0.5):
        super(DropConnect, self).__init__()
        self.p = p  # 無効化確率

    def forward(self, weights):
        # 重みに対応するマスクを生成
        mask = torch.bernoulli((1 - self.p) * torch.ones_like(weights))
        
        # 重みにマスクを適用して再スケール
        return weights * mask / (1 - self.p + 1e-8)

# DropConnectを使用したモデルの定義
class DropConnectModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropconnect_prob=0.5):
        super(DropConnectModel, self).__init__()
        self.fc1_weights = nn.Parameter(torch.randn(input_dim, hidden_dim))  # 重み
        self.fc1_bias = nn.Parameter(torch.zeros(hidden_dim))  # バイアス
        self.dropconnect = DropConnect(p=dropconnect_prob)  # DropConnectの適用
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        # DropConnect適用後の重みを使用して計算
        fc1_weights = self.dropconnect(self.fc1_weights)
        x = torch.matmul(x, fc1_weights) + self.fc1_bias
        x = torch.relu(x)
        x = self.fc2(x)
        return x

# モデルのインスタンス化
model = DropConnectModel(input_dim=256, hidden_dim=128, output_dim=10, dropconnect_prob=0.5)

# 損失関数とオプティマイザの設定
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# ダミーデータの生成
inputs = torch.randn(32, 256)  # バッチサイズ32, 入力次元256
targets = torch.randint(0, 10, (32,))  # 10クラス分類

# トレーニングループ
for epoch in range(5):
    optimizer.zero_grad()  # 勾配の初期化
    outputs = model(inputs)  # モデルのフォワードパス
    loss = criterion(outputs, targets)  # 損失の計算
    loss.backward()  # バックプロパゲーション
    optimizer.step()  # パラメータの更新

    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")  # エポックごとの損失を表示
Epoch 1, Loss: 13.5242
Epoch 2, Loss: 9.8219
Epoch 3, Loss: 11.0604
Epoch 4, Loss: 16.1125
Epoch 5, Loss: 12.9608

ドロップアウトとの違い

  • ドロップコネクトとドロップアウトのどちらが効果的かは、モデルの構造やデータセットの特性、ハイパーパラメータの設定などによって変わることがあり、一般的には、ドロップアウトが広く使用されており、シンプルなモデルやデータセットに対して効果的です。
  • ドロップコネクトは、特定の状況ではドロップアウトよりも効果的な場合がありますが、一般的にはドロップアウトの方が安定した性能を示すことが多いです。

同時に使用する場合のシナリオ

  • 異なる層に異なる正則化手法を適用
    • 例えば、入力層や中間層にドロップアウトを適用し、出力層にドロップコネクトを適用することが考えられます。これにより、モデルの異なる部分に対して異なる正則化効果を持たせることができます。
  • 複数の正則化手法を組み合わせて使用
    • 例えば、変分ドロップアウトを適用した後に、ドロップコネクトを適用することで、より強力な正則化効果を得ることができます。ただし、過度な正則化はモデルの性能を低下させる可能性があるため、慎重に設定する必要があります。

Concrete Dropout

Concrete Dropoutは、トレーニング中に最適なドロップアウト率を学習することで、従来のドロップアウトの固定的な設定を克服した手法です。不確実性推定やベイズニューラルネットワークの分野で特に有効であり、タスクやモデルに応じた柔軟な適用が可能です。数式やコードを基に設計の原理を理解することで、実用性を最大限に引き出せます。

動作原理

数式：

  • ドロップアウト率の学習可能化
    • ドロップアウト率 $\pi$ を直接学習する代わりに、学習可能なパラメータ $z$ を導入し、次のように変換します

$$π=σ{(z)}$$

  • $σ(z)$：シグモイド関数。$z$：学習可能なパラメータ。
  • Concrete分布
    • ドロップアウト操作を微分可能にするため、Concrete分布（スムーズな確率分布）を利用します。Concrete分布を用いたマスク $m$ は以下のように定義されます。

$$m = \text{sigmoid} \left( \frac{1}{t} \left( \log \pi – \log (1 – \pi) + \log u – \log (1 – u) \right) \right)$$

  • $t$：温度パラメータ（スムージングを制御）。
  • $u$∼Uniform(0,1): 乱数。（Uniform は一様分布を意味し、値が等確率で発生する確率分布です。）
  • スパース化された出力
    • Concrete Dropout適用後の出力は次のように計算されます。

$$x’=m⋅x$$

  • $x$：入力データ。：$x’$=ドロップアウト後の出力。
  • 正則化項
    • ドロップアウト率 $\pi$ を正則化するため、損失関数に以下の項を追加します。

$$\mathcal{L}_{\text{dropout}} = \lambda \cdot \sum_{i} \pi_i$$

  • $λ$：正則化強度を制御するハイパーパラメータ。

Concrete Dropoutの利点と欠点

利点：

利点説明
学習可能なドロップアウト率各ニューロンに最適な無効化確率を動的に調整可能で、モデルの適応力を向上。
柔軟性の向上固定ハイパーパラメータに依存せず、適応的にモデルの正則化を調整できる。
微分可能な設計Concrete分布を利用して、確率的な操作を微分可能にし、効率的な学習を実現。

欠点：

欠点説明
計算コストの増加Concrete分布に基づく計算と正則化項の追加により、通常のドロップアウトと比較して計算負荷が増加。
実装の複雑さ通常のドロップアウトと比較して、実装が複雑で開発やチューニングに手間がかかる。

適用例

適用例説明
不確実性推定Concrete Dropoutはベイズニューラルネットワークで使用され、予測の不確実性を推定可能。
タスク全般構造が複雑なモデル（例: Transformerや深層全結合モデル）で適用可能。

論文

Concrete Dropout
Dropout is used as a practical tool to obtain uncertainty estimates in large vision models and reinforcement learning (R...
arxiv.org
  • ドロップアウト確率の自動最適化
    • Concrete Dropoutは、従来のように手動で調整する必要があったドロップアウト確率を、自動で最適化できる手法です。ベイズ的なアプローチと新しい緩和技術を活用することで、大規模なモデルや動的に変化するデータ環境でも、効率的かつ正確な不確実性の推定を実現します。
  • 不確実性の種類を明確に分離
    • Concrete Dropoutは、データの不足で生じる「エピステミック不確実性」と、ノイズなどの要因による「アレータリック不確実性」を明確に区別し、それぞれを個別にモデル化できます。この分離によって、不確実性の正確な把握が可能となり、モデルの性能や安全性の向上につながります。
  • 強化学習での不確実性の動的適応
    • Concrete Dropoutは、強化学習でエージェントがデータの増加に応じて不確実性を自動的に調整できる仕組みを提供します。この特性により、過剰な探索を防ぎながら効率的で安全な行動が可能となり、高リスクのタスクにも適用しやすい手法です。

Concrete Dropout（PyTorch）：

ライブラリのインポート

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

Concrete Dropoutレイヤーの定義

class ConcreteDropout(nn.Module):
    def __init__(self, input_dim, initial_dropout_rate=0.1, weight_regularizer=1e-6, dropout_regularizer=1e-6):
        super(ConcreteDropout, self).__init__()
        self.logit_dropout_rate = nn.Parameter(torch.full((1,), torch.logit(torch.tensor(initial_dropout_rate))))
        self.weight_regularizer = weight_regularizer
        self.dropout_regularizer = dropout_regularizer

    def forward(self, x):
        # ドロップアウト率の計算（シグモイドを使用）
        dropout_rate = torch.sigmoid(self.logit_dropout_rate)
        
        # Concrete分布によるマスク生成
        uniform_random = torch.rand_like(x)
        eps = 1e-8  # 数値安定性のための小さな値
        mask = torch.sigmoid(
            (torch.log(dropout_rate + eps) - torch.log(1 - dropout_rate + eps) +
             torch.log(uniform_random + eps) - torch.log(1 - uniform_random + eps)) / 0.1
        )
        
        # 出力のスパース化
        output = x * mask

        # 正則化項の計算
        self.regularization_loss = self.compute_regularization(dropout_rate, x)
        return output

    def compute_regularization(self, dropout_rate, x):
        # 正則化項の計算
        weight_reg = self.weight_regularizer * torch.sum(x**2)
        dropout_reg = self.dropout_regularizer * torch.sum(dropout_rate)
        return weight_reg + dropout_reg

Concrete Dropoutを使用したモデルの定義

class ConcreteDropoutModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, initial_dropout_rate=0.1):
        super(ConcreteDropoutModel, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.concrete_dropout = ConcreteDropout(hidden_dim, initial_dropout_rate)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.concrete_dropout(x)  # Concrete Dropoutの適用
        x = self.fc2(x)
        return x

モデルのインスタンス化

model = ConcreteDropoutModel(input_dim=256, hidden_dim=128, output_dim=10)

損失関数とオプティマイザの設定

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

ダミーデータの生成

inputs = torch.randn(32, 256)  # バッチサイズ32, 入力次元256
targets = torch.randint(0, 10, (32,))  # 10クラス分類

トレーニングループ

for epoch in range(5):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, targets) + model.concrete_dropout.regularization_loss  # 正則化項を加える
    loss.backward()
    optimizer.step()

    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")
Epoch 1, Loss: 2.3007
Epoch 2, Loss: 2.2929
Epoch 3, Loss: 2.2617
Epoch 4, Loss: 2.2867
Epoch 5, Loss: 2.2890

Concrete Dropoutにおける予測の不確実性を導き出すための手法

# 予測の不確実性を導き出すための関数
def predict_with_uncertainty(model, inputs, n_iter=100):
    model.train()  # ドロップアウトを有効にするためにトレーニングモードに設定
    predictions = []

    for _ in range(n_iter):
        outputs = model(inputs)
        predictions.append(outputs.unsqueeze(0))

    predictions = torch.cat(predictions, dim=0)
    prediction_mean = predictions.mean(dim=0)
    prediction_variance = predictions.var(dim=0)
    
    return prediction_mean, prediction_variance

# 新しいダミーデータで予測の不確実性を計算
new_inputs = torch.randn(32, 256)  # 新しいバッチサイズ32, 入力次元256
mean, variance = predict_with_uncertainty(model, new_inputs)

print("Prediction Mean:", mean[:3])
print("Prediction Variance:", variance[:3])
Prediction Mean: tensor([[-0.0513, -0.1431, -0.0006,  0.0825,  0.0271, -0.0612,  0.0117,  0.0872,
          0.0011, -0.0779],
        [-0.0319, -0.1029,  0.0106,  0.0667,  0.0195, -0.0470, -0.0198,  0.0447,
         -0.0265, -0.0754],
        [-0.0409, -0.1152, -0.0281,  0.0253,  0.0300, -0.0621,  0.0017,  0.0130,
         -0.0510, -0.0877]], grad_fn=<SliceBackward0>)
Prediction Variance: tensor([[0.0040, 0.0066, 0.0049, 0.0063, 0.0053, 0.0026, 0.0040, 0.0054, 0.0052,
         0.0049],
        [0.0043, 0.0054, 0.0029, 0.0019, 0.0052, 0.0039, 0.0031, 0.0049, 0.0041,
         0.0025],
        [0.0061, 0.0070, 0.0037, 0.0050, 0.0056, 0.0045, 0.0035, 0.0034, 0.0043,
         0.0032]], grad_fn=<SliceBackward0>)

Concrete Dropoutは、ドロップアウト率を学習可能なパラメータとして扱い、トレーニング中に最適化することで、より柔軟な正則化を実現します。予測の不確実性を導き出すためには、ドロップアウトを有効にしたまま複数回の予測を行い、その結果の分散を計算します。これにより、モデルの予測の信頼性を評価することができます。

エピステミック不確実性とアレータリック不確実性

データの不足で生じる「エピステミック不確実性」と、ノイズなどの要因による「アレータリック不確実性」を明確に区別します。

import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import japanize_matplotlib

# 合成データ
np.random.seed(42)
torch.manual_seed(42)
x_train = np.linspace(-3, 3, 30)
y_train = x_train**2 + np.random.normal(0, 0.5, size=x_train.shape)  # アレアトリックノイズを追加
x_test = np.linspace(-5, 5, 100)

x_train_tensor = torch.tensor(x_train[:, np.newaxis], dtype=torch.float32)
y_train_tensor = torch.tensor(y_train[:, np.newaxis], dtype=torch.float32)
x_test_tensor = torch.tensor(x_test[:, np.newaxis], dtype=torch.float32)

# ベイズニューラルネットワークの定義
class BayesianLinear(nn.Module):
    def __init__(self, in_features, out_features):
        super().__init__()
        self.mu = nn.Parameter(torch.zeros(in_features, out_features))
        self.rho = nn.Parameter(torch.zeros(in_features, out_features))
        self.bias_mu = nn.Parameter(torch.zeros(out_features))
        self.bias_rho = nn.Parameter(torch.zeros(out_features))
        
        self.epsilon = torch.distributions.Normal(0, 1)

    def forward(self, x):
        # 重みとバイアスのサンプリング
        weights = self.mu + torch.log1p(torch.exp(self.rho)) * self.epsilon.sample(self.mu.size())
        bias = self.bias_mu + torch.log1p(torch.exp(self.bias_rho)) * self.epsilon.sample(self.bias_mu.size())
        return torch.matmul(x, weights) + bias

class BayesianNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.blinear1 = BayesianLinear(1, 20)
        self.relu = nn.ReLU()
        self.blinear2 = BayesianLinear(20, 1)

    def forward(self, x):
        x = self.blinear1(x)
        x = self.relu(x)
        return self.blinear2(x)

# モデル、損失関数、オプティマイザの設定
model = BayesianNN()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
loss_fn = nn.MSELoss()

# トレーニング
epochs = 500
for epoch in range(epochs):
    model.train()
    optimizer.zero_grad()
    output = model(x_train_tensor)
    loss = loss_fn(output, y_train_tensor)
    loss.backward()
    optimizer.step()

# 不確実性推定のための複数回の予測
model.eval()
predictions = []
with torch.no_grad():
    for _ in range(100):
        predictions.append(model(x_test_tensor).numpy().flatten())

# 不確実性の計算
predictions = np.array(predictions)
mean_prediction = predictions.mean(axis=0)
epistemic_uncertainty = predictions.std(axis=0)  # 予測のばらつき
aleatoric_uncertainty = 0.5  # 合成データにおける固定ノイズ

# 結果のプロット
plt.figure(figsize=(10, 6))
plt.plot(x_train, y_train, 'kx', label="トレーニングデータ")
plt.plot(x_test, mean_prediction, 'b', label="平均予測")
plt.fill_between(x_test, 
                 mean_prediction - epistemic_uncertainty, 
                 mean_prediction + epistemic_uncertainty, 
                 color='blue', alpha=0.2, label="エピステミック不確実性")
plt.fill_between(x_test, 
                 mean_prediction - aleatoric_uncertainty, 
                 mean_prediction + aleatoric_uncertainty, 
                 color='green', alpha=0.2, label="アレアトリック不確実性")
plt.legend()
plt.title("エピステミック不確実性 vs アレアトリック不確実性")
plt.show()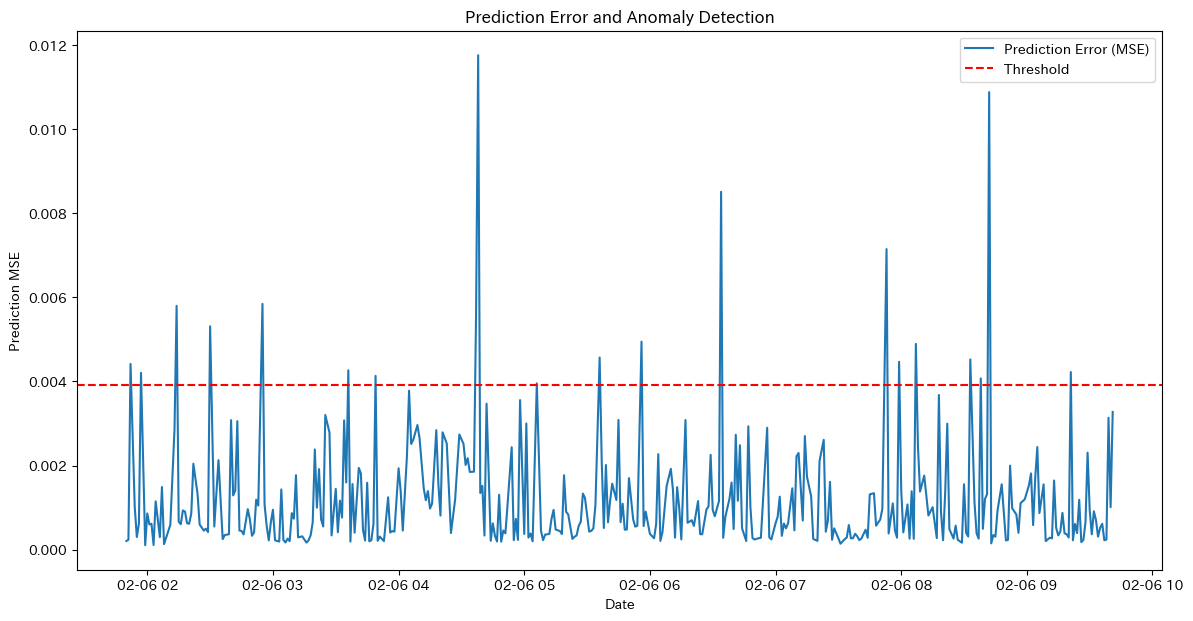

これにより予測の不確実性を推定可能にし、モデルの性能向上に貢献することができます。

AlphaDropout

AlphaDropoutは、SELU（Scaled Exponential Linear Units）アクティベーション関数に最適化された正則化手法です。従来のドロップアウトでは、ニューロンの出力を無効化することでデータ分布が乱れ、SELUの自己正規化特性が失われる場合があります。AlphaDropoutは、この課題を解決するため、ドロップアウト後の出力を元の分布に近い形に補正することで、学習の安定性を維持します。

SELUとは？

  • SELUは特に深いネットワーク構造に適しており、勾配消失問題を防ぎつつ、高速な学習を実現するために設計されています。これは、従来のReLUやLeaky ReLUの進化版と考えられ、活性化関数選択の一つとして強力な選択肢です。

動作原理

数式：

  • 入力値の正則化
    • 入力値 $x$ をランダムに無効化（ドロップアウト）する際、無効化された値をスケール補正します。

$$x_i’ =
\begin{cases}
x_i & \text{with probability } 1 – p, \\
\alpha \cdot \mu & \text{with probability } p,
\end{cases}$$

  • $p$：ドロップアウト率（無効化確率）。
  • $α$：SELUの負のスケール係数（$\alpha \approx 1.67326$）。
  • $μ$：データ分布の平均値。
  • スケール補正
    • ドロップアウトによる分散の増加を補正するため、次のスケーリングを行います。

$${x_i}” = \frac{x_i’}{\sqrt{(1 – p) + p \cdot \alpha^2}}$$

  • 出力の計算
    • ドロップアウト後の値 $x”_i$ は、SELUアクティベーション関数を通して自己正規化されます。

$$y_i=\text{SELU}({x_i}′′)$$

SELUの定義

$$\text{SELU}(x) =
\begin{cases}
\lambda x & \text{if } x > 0, \\
\lambda \alpha (e^x – 1) & \text{if } x \leq 0,
\end{cases}$$

  • $λ$：スケール係数（$\lambda \approx 1.0507$）。

特徴

  • 自己正規化の維持
    • SELUの自己正規化特性を維持するため、ドロップアウト後のデータ分布を補正します。
  • SELUとの相性
    • SELUは深いニューラルネットワークでの勾配消失や爆発を抑制するために設計されています。AlphaDropoutは、この特性を損なわずに過学習を防ぎます。

AlphaDropoutの利点と欠点

利点：

利点詳細
SELUとの互換性データ分布を補正することで、SELUの自己正規化特性を維持。
汎化性能の向上過学習を防ぎ、安定した学習を提供。

欠点：

欠点詳細
SELU依存他の活性化関数（ReLUやLeakyReLUなど）との組み合わせでは有効性が低い。
計算コストデータ補正のため、若干の計算負荷が増加。

適用シナリオ：

適用シナリオ説明
SELUを使用したモデル深いニューラルネットワークや自己正規化ニューラルネットワーク（Self-Normalizing Neural Networks）。
安定性が重要なタスク深いモデルや長期依存関係を持つタスクで学習の安定性を向上。

AlphaDropout（PyTorch）：

ライブラリのインポート

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

AlphaDropoutとSELUを使用したモデルの定義

class AlphaDropoutModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, dropout_prob=0.1):
        super(AlphaDropoutModel, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.alpha_dropout = nn.AlphaDropout(p=dropout_prob)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        x = F.selu(self.fc1(x))  # SELUアクティベーション関数
        x = self.alpha_dropout(x)  # AlphaDropoutを適用
        x = self.fc2(x)
        return x

AlphaDropoutはSELU活性化関数と組み合わせて使用することで、安定したトレーニングが可能になります。

モデルのインスタンス化

model = AlphaDropoutModel(input_dim=256, hidden_dim=128, output_dim=10, dropout_prob=0.1)

損失関数とオプティマイザの設定

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

ダミーデータの生成

inputs = torch.randn(32, 256)  # バッチサイズ32, 入力次元256
targets = torch.randint(0, 10, (32,))  # 10クラス分類

トレーニングループ

for epoch in range(5):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    loss.backward()
    optimizer.step()

    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")
Epoch 1, Loss: 2.4118
Epoch 2, Loss: 2.1843
Epoch 3, Loss: 1.9395
Epoch 4, Loss: 1.7148
Epoch 5, Loss: 1.5416

AlphaDropoutの効果の検証

import matplotlib.pyplot as plt

# ダミーデータ
inputs = torch.randn(1000, 256)

# ドロップアウト適用前後の分布
with torch.no_grad():
    outputs_before = inputs.numpy()
    outputs_after = dropout(inputs).numpy()

# ヒストグラムプロット
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.hist(outputs_before.flatten(), bins=50, color='blue', alpha=0.7)
plt.title("Before AlphaDropout")
plt.subplot(1, 2, 2)
plt.hist(outputs_after.flatten(), bins=50, color='green', alpha=0.7)
plt.title("After AlphaDropout")
plt.show()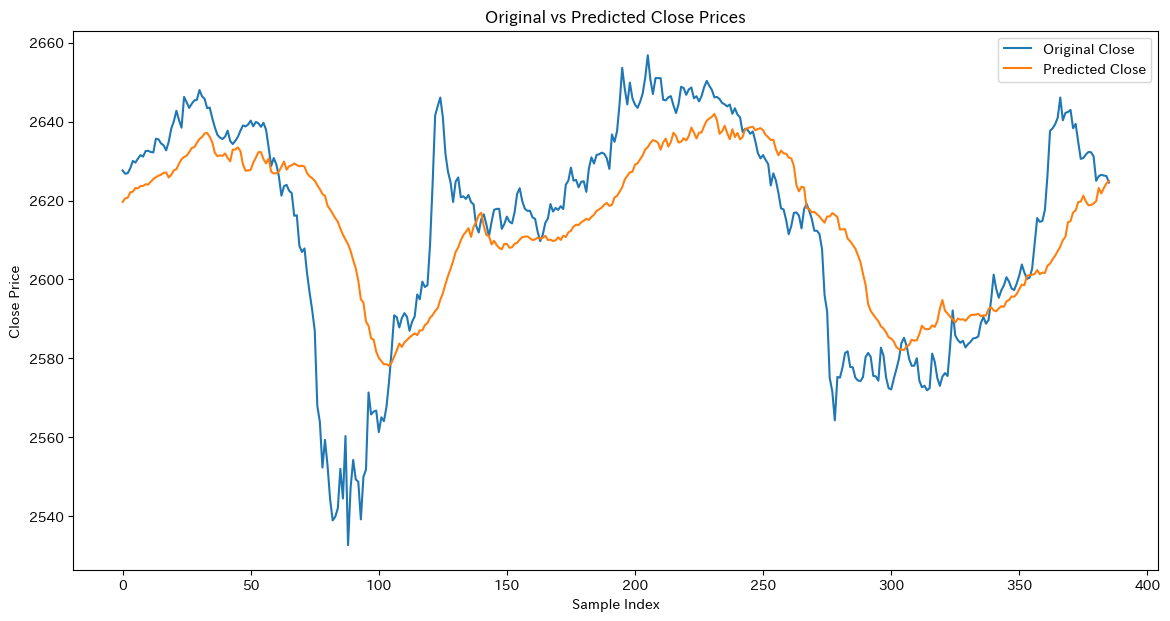
活性化関数としてのSELU

SELU（Scaled Exponential Linear Unit）は、Klambauerらによって提案された活性化関数で、ニューラルネットワークの学習において自己正規化を実現するために設計されています。

SELU活性化関数は、深いニューラルネットワークにおいて自己正規化を実現し、勾配消失や勾配爆発を防ぐ効果的な手法です。適切な重みの初期化や入力データの正規化、そしてAlphaDropoutとの併用により、その効果を最大限に引き出すことができます。

SELUの数式：

$$\text{SELU}(x) =
\begin{cases}
\lambda x & \text{if } x > 0, \\
\lambda \alpha (e^x – 1) & \text{if } x \leq 0,
\end{cases}$$

  • $λ$ はスケール係数で、値は約 1.0507。
  • $α$ はシフト係数で、値は約 1.67326。

パラメータ $λ$ と $α$ の意味

これらの定数 $λ$ と $α$ は、ネットワークの各層での出力の平均と分散が一定になるように調整されています。これにより、自己正規化（Self-Normalizing）を実現します。

  • 自己正規化
    • 各層の出力が特定の平均と分散に収束し、深い層でもデータ分布が安定します。
  • 勾配消失・爆発の防止
    • 活性化関数が自己正規化することで、勾配のスケールが適切に保たれます。

特徴：

特徴詳細説明
自己正規化特性活性化関数自体がデータの正規化を行い、バッチ正規化（Batch Normalization）が不要になる場合があります。
深いネットワークへの適用SELUは深い層を持つネットワークでも効果的に機能し、学習の安定性を向上させます。
非線形性の確保負の値に対して指数関数的な変化を持つため、非線形性が強化されます。

用途：

  • 主に深いニューラルネットワークのトレーニングを安定させるために使用されます。
  • SELUを使用する場合、重みの初期化としてLeCun正規化を使用することが推奨されます。
  • LeCun正規化とSELUを組み合わせることで、ニューラルネットワークのトレーニングがさらに安定します。
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# PyTorchを使ってSELU関数を定義する
selu = nn.SELU()

# Apple Silicon GPUが利用可能かどうかをチェック
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")

# x値の生成 (GPUに移動)
x = torch.linspace(-10, 10, 100).to(device)

# SELU関数をxに適用
y_selu = selu(x)

# Plotting
plt.figure(figsize=(15, 5))

# SELU plot (CPUに戻してからNumPyに変換)
plt.subplot(1, 3, 2)
plt.plot(x.cpu().detach().numpy(), y_selu.cpu().detach().numpy(), label="SELU", color="blue")
plt.title("SELU Function")
plt.xlabel("x")
plt.ylabel("SELU(x)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()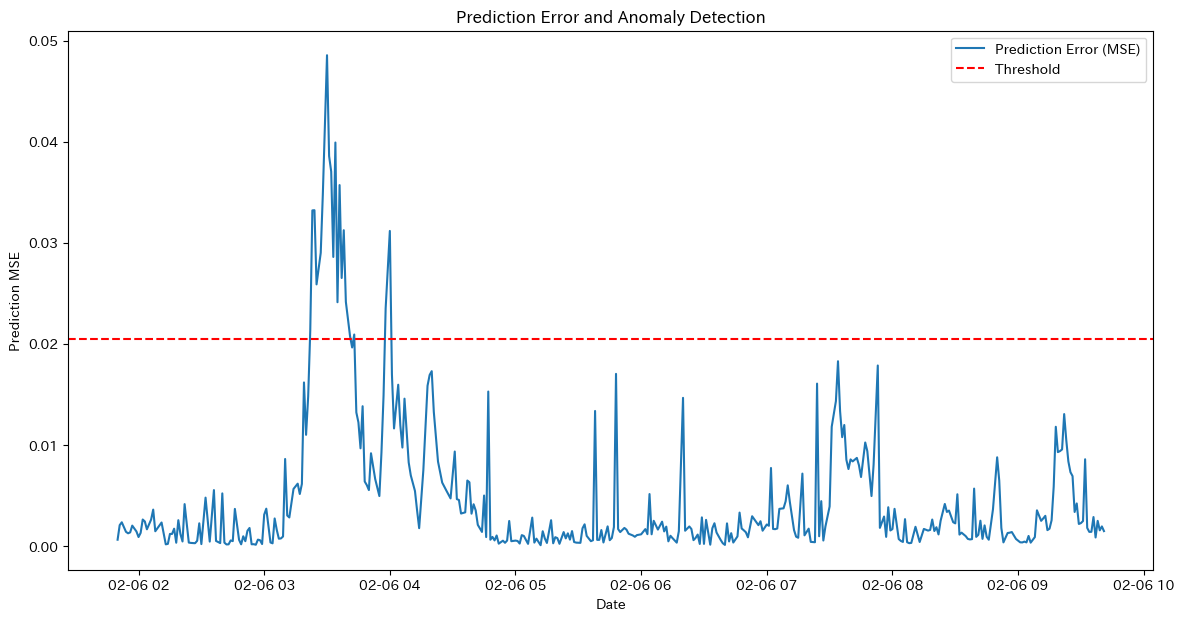

SELUを使用する際の注意点：

注意点詳細説明
ドロップアウトの使用通常のドロップアウトはSELUの自己正規化特性を損なう可能性があるため、AlphaDropoutを使用することが推奨されます。
バッチ正規化の不要性SELUは自己正規化を行うため、バッチ正規化（Batch Normalization）は一般的に使用しません。
入力データの正規化入力データは、平均0、分散1に正規化することが望ましいです。

SELUと他の活性化関数の比較：

活性化関数特徴SELUとの違い
ReLU簡単で計算コストが低いが、負の値に対して勾配がゼロになる（Dead Neurons問題）。SELUは負の値も指数関数的に扱えるため、表現力が豊富で深いネットワークでの学習が安定。
ELU負の値を指数関数的に処理し、ReLUのDead Neurons問題を緩和。自己正規化特性は持たない。SELUは自己正規化特性を持ち、学習の安定性が向上するため、追加の正規化手法が不要な場合もある。
Leaky ReLU負の値に対して小さな勾配を保ち、Dead Neurons問題を軽減。SELUはLeaky ReLUよりも強力な自己正規化効果を持ち、バッチ正規化なしで深いネットワークでも効果的に機能。

SELUのメリットとデメリット：

メリット説明
勾配消失や爆発の抑制深いネットワークでも勾配消失や爆発を効果的に抑え、学習を安定化します。
バッチ正規化なしでの学習安定化自己正規化特性により、バッチ正規化が不要になる場合があり、モデルの設計を簡素化できます。
汎化性能の向上過学習を防ぎ、未知のデータへの適応力が向上する場合があります。
デメリット説明
効果が限定的ネットワークやデータセットによってはSELUの効果が十分に発揮されない場合があります。
特定の条件が必要重みの適切な初期化（平均0、分散1）やデータの正規化が求められます。
正則化手法との併用に注意が必要通常のドロップアウトはSELUの自己正規化特性を損なう可能性があるため、AlphaDropoutを使用する必要があります。

続いてSELUで使われるLeCun正規化の説明を行い、その後で合わせて実装例を紹介します。

重みの初期化（LeCun正規化）

SELUを使用する際には、LeCun正規化に基づいた重みの初期化が推奨されています。これは、自己正規化が適切に機能するための条件の一つです。

  • LeCun正規化
    • 重みを以下の分散で初期化します。

$$\text{Var}(w) = \frac{1}{n_{\text{in}}}$$

  • $w$：重み。$n_{\text{in}}$​：前の層（入力層）のユニット数。

この分散に基づいた初期化は、出力の分散を一定に保つように設計されており、自己正規化をサポートします。

特徴：

  • ゼロ平均・一定分散を保つため、勾配消失や爆発のリスクを軽減。
  • SELUのスケール係数 $λ$ と組み合わせることで、各層の出力を正規化。

LeCun正規化の実装例

import torch
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns

# LeCun正規化に基づく重みの初期化を関数化（正規分布を使用）
def lecun_normal_initialization(tensor, fan_in):
    """
    LeCun正規化を適用する関数（正規分布を使用）
    tensor: 初期化するテンソル
    fan_in: 層への入力ユニット数
    """
    # 標準偏差を計算
    std = (1 / fan_in) ** 0.5  # sqrt(1 / fan_in)
    return torch.nn.init.normal_(tensor, mean=0.0, std=std)

# サンプルネットワークの重みを初期化
fan_in = 128  # 入力ユニット数
fan_out = 64  # 出力ユニット数
weight_tensor = torch.empty((fan_out, fan_in))  # 初期化対象のテンソル (fan_out, fan_in)

# LeCun正規化の適用（正規分布を使用）
lecun_normal_initialization(weight_tensor, fan_in)

# 初期化結果を確認
print("LeCun正規化後の重み（正規分布）:")
print(weight_tensor)

# 重みの分布をヒストグラムと確率密度関数として可視化
plt.figure(figsize=(10, 6))
# ヒストグラムのプロット
sns.histplot(weight_tensor.numpy().flatten(), bins=30, color='blue', kde=True, edgecolor='black', stat='density', label='ヒストグラム')
# 確率密度関数のプロット
sns.kdeplot(weight_tensor.numpy().flatten(), color='red', fill=True, alpha=0.3, label='確率密度関数')
plt.title('LeCun正規化後の重みの分布と確率密度関数（正規分布）')
plt.xlabel('重みの値')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()
LeCun正規化後の重み（正規分布）:
tensor([[-0.1320, -0.0032,  0.1393,  ..., -0.1146, -0.1325,  0.0130],
        [ 0.0350, -0.0101,  0.0117,  ..., -0.0594,  0.1083,  0.1652],
        [-0.0051, -0.0122,  0.1234,  ..., -0.0679, -0.0010, -0.0699],
        ...,
        [-0.0714, -0.0946, -0.0554,  ..., -0.0033,  0.0022, -0.0089],
        [-0.0839, -0.0950, -0.0469,  ..., -0.0766,  0.0917,  0.0073],
        [ 0.0481,  0.0825, -0.0577,  ..., -0.0129,  0.0190,  0.1045]])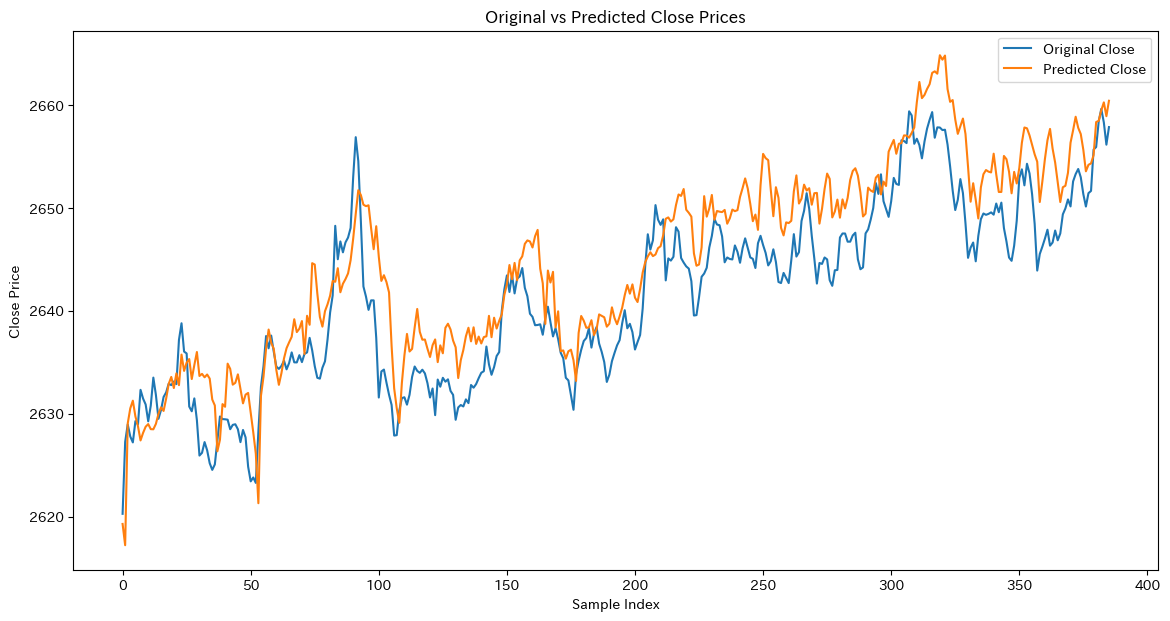

他の初期化手法との比較：

初期化手法特徴適用例
LeCun正規化SELUに最適化。出力の分散を一定に保つ。SELUを使用するモデル
Xavier初期化SigmoidやTanhで適切に機能。浅いネットワーク全般
He初期化ReLUやLeaky ReLUで適切に機能。ReLU活性化を使うモデル
ランダム初期化一様分布や正規分布でランダムに設定。初期化の質が悪いと学習が不安定になる。特に推奨されない

SELU（PyTorch）：

次のコードを用いてSELU（Scaled Exponential Linear Unit）活性化関数を使用したニューラルネットワークモデルを定義し、LeCun正規化に基づいた重みの初期化を行い、トレーニングを実行します。

ライブラリのインポート

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

SELUを使用したモデルの定義

class SELUNet(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(SELUNet, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)
        
        # 重みの初期化（LeCun正規化）
        self.init_weights()

    def init_weights(self):
        # LeCun正規化に基づく初期化
        fan_in = self.fc1.weight.size(1)
        nn.init.normal_(self.fc1.weight, mean=0, std=(1.0 / fan_in**0.5))
        fan_in = self.fc2.weight.size(1)
        nn.init.normal_(self.fc2.weight, mean=0, std=(1.0 / fan_in**0.5))
    
    def forward(self, x):
        x = self.fc1(x)
        x = F.selu(x)  # SELU活性化関数
        x = self.fc2(x)
        return x

モデルのインスタンス化

model = SELUNet(input_dim=256, hidden_dim=128, output_dim=10)

損失関数とオプティマイザの設定

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

ダミーデータの生成

inputs = torch.randn(32, 256)  # バッチサイズ32, 入力次元256
targets = torch.randint(0, 10, (32,))  # 10クラス分類

トレーニングループ

for epoch in range(10):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    loss.backward()
    optimizer.step()
    
    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")
Epoch 1, Loss: 2.6168
Epoch 2, Loss: 2.4914
…
Epoch 9, Loss: 1.7378
Epoch 10, Loss: 1.6469

論文：

Self-Normalizing Neural Networks
Deep Learning has revolutionized vision via convolutional neural networks (CNNs) and natural language processing via rec...
arxiv.org

SNNとは？

  • 自己正規化機能の導入
    • SNNは、SELUsという活性化関数を使うことで、各層のニューロンの平均と分散を自動的に整えます。この仕組みにより、従来必要だったバッチ正規化が不要になり、計算を効率化できる点が特徴です。
  • 深層ネットワークへの適用可能性
    • 従来のFNNは深くするほど学習が不安定になる課題がありましたが、SNNはその問題を解決しました。安定した学習が可能になり、高次元の複雑な特徴を深いネットワークで効果的に学習できるようになりました。
  • 優れた実験結果
    • SNNはUCIデータセットでの評価において、24種類の機械学習手法を上回る結果を示しました。特に、大規模データセットで高い精度を発揮し、計算効率の向上も確認されています。

Zoneout

Zoneoutは、RNN、LSTM、GRUの学習を正則化し、時間的安定性を高める手法です。ランダムに過去の状態を保持することで、過学習を防ぎつつ、時間的依存性を考慮した安定した学習を可能にします。数式や実装例を通じてその動作を理解することで、時系列データに対するモデル性能を向上させることができます。

動作原理

数式による表現：

  • Zoneoutは、隠れ状態 $h_t$​ をランダムに過去の状態 $h_{t-1}$​ に保持することで機能します。
  • 通常のRNNの隠れ状態更新式
    • 通常のRNNの隠れ状態は次のように更新されます。

$$h_t = f(h_{t-1}, x_t)$$

  • $h_t$​：現在の隠れ状態。$h_{t−1}$​：前の隠れ状態。$x_t$​：現在の入力。
  • $f$：RNNの更新関数（例：LSTM、GRUなど）。
  • Zoneoutによる状態保持
    • Zoneoutでは、隠れ状態 $h_t$​ を次のように定義します。

$$h_t = m \odot h_t + (1 – m) \odot h_{t-1}$$

  • $m∼Bernoulli(1−p)$：保持マスク（0または1）。
  • $p$：Zoneout率（保持する確率）。$⊙$：要素ごとの積。
  • マスク $m$ の値が1の場合、現在の隠れ状態 $h_t$ を使用。
  • マスク $m$ の値が0の場合、過去の状態 $h_{t-1}$ を保持。
  • Zoneoutの効果
    • 時間的な安定性を維持：一部の状態を過去の状態に保持することで、急激な変化を防止。
    • 過学習の防止：ランダムな保持による正則化。
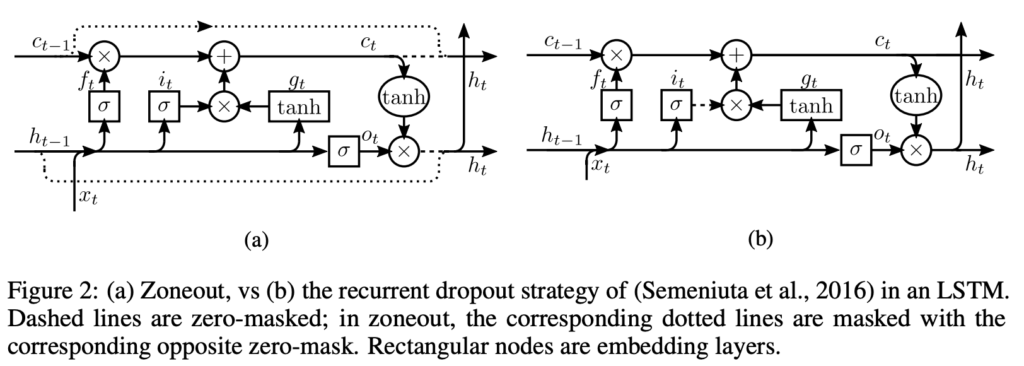
論文：「Zoneout: Regularizing RNNs by Randomly Preserving Hidden Activations」
より抜粋　図2: (a) LSTMにおけるゾーンアウト、(b) (Semeniuta et al., 2016)のリカレント・ドロップアウト戦略。ゾーンアウトでは、対応する点線は対応する反対側のゼロマスクでマスクされる。対応する反対側のゼロマスクでマスクされる。長方形のノードは埋め込み層。

Zoneoutの利点と欠点

利点：

利点説明
時間的安定性状態を過去に保持することで、隠れ状態の急激な変化を防ぎ、学習の安定性を向上させます。
過学習の防止ランダム性を導入することで、モデルの汎化性能を高め、過学習を防ぎます。
時系列データへの適性時間的依存性を考慮した設計により、RNN、LSTM、GRUなどのモデルで効果を発揮します。

欠点：

欠点説明
計算コストの増加Zoneoutのランダムマスク生成と適用により、通常のRNNより若干の計算負荷が増加します。
設計の複雑さ通常のRNNセルに比べて実装が複雑であり、設計・調整に追加の労力が必要です。

Zoneoutの適用例：

適用例説明
自然言語処理（NLP）RNNベースのモデルで文脈を保持しつつ、過学習を防ぎます。
音声認識時系列データの長期依存関係を学習するモデルで、Zoneoutにより安定性が向上します。
金融時系列予測株価や市場データなど、長期的な時間的依存性が重要なタスクにおいて、Zoneoutが効果的に動作します。

論文：

Zoneout: Regularizing RNNs by Randomly Preserving Hidden Activations
We propose zoneout, a novel method for regularizing RNNs. At each timestep, zoneout stochastically forces some hidden un...
arxiv.org
  • 新しい正則化手法「Zoneout」の提案
    • Zoneoutは、RNNの隠れ層の一部をランダムに前の値のまま保持することで、モデルの学習を安定させる新しい正則化手法です。この仕組みにより、情報が途切れずに流れ続け、汎化性能を高めながら消失勾配の問題を軽減します。
  • 他の正則化手法との違いと強み
    • Zoneoutは、DropoutやリカレントDropoutと異なり、情報や勾配の流れを妨げないため、長期的な依存関係をしっかりと保持できます。この特性により、LSTMやGRUを含むさまざまなRNNアーキテクチャで効果的に利用できます。
  • タスクでの高い性能と実証
    • Zoneoutは、Penn TreebankやText8といった言語モデリングや、Permuted Sequential MNISTの分類タスクで優れた性能を示しました。特に、リカレントバッチ正規化と組み合わせることで、最先端の成果を達成しました。

Zoneout（PyTorch）：

次のコードは、Zoneoutを定義し、RNNの隠れ状態に対してドロップアウトを適用することで、過学習を防ぐための正則化手法を行なったニューラルネットワークの一例です。

ライブラリのインポート

import torch
import torch.nn as nn
import torch.optim as optim

ZoneoutRNNCellクラスの定義

class ZoneoutRNNCell(nn.Module):
    def __init__(self, base_cell, zoneout_prob=0.1):
        """
        Zoneoutを適用するRNNセル
        :param base_cell: LSTMやGRUなどの基本RNNセル
        :param zoneout_prob: Zoneoutの確率
        """
        super(ZoneoutRNNCell, self).__init__()
        self.base_cell = base_cell
        self.zoneout_prob = zoneout_prob

    def forward(self, input, hidden):
        # 通常のRNNセルの出力
        next_hidden = self.base_cell(input, hidden)

        # Zoneoutを適用
        if isinstance(hidden, tuple):  # LSTMの場合
            h, c = hidden
            h_next, c_next = next_hidden

            # 隠れ状態 h にZoneoutを適用
            zoneout_mask = torch.bernoulli((1 - self.zoneout_prob) * torch.ones_like(h))
            h_zoneout = zoneout_mask * h_next + (1 - zoneout_mask) * h

            # セル状態 c はそのまま
            return h_zoneout, c_next
        else:  # GRUの場合
            zoneout_mask = torch.bernoulli((1 - self.zoneout_prob) * torch.ones_like(hidden))
            hidden_zoneout = zoneout_mask * next_hidden + (1 - zoneout_mask) * hidden
            return hidden_zoneout

ZoneoutRNNModelクラスの定義

class ZoneoutRNNModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim, zoneout_prob=0.1):
        super(ZoneoutRNNModel, self).__init__()
        self.zoneout_cell = ZoneoutRNNCell(nn.LSTMCell(input_dim, hidden_dim), zoneout_prob)
        self.fc = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        batch_size = x.size(0)
        seq_len = x.size(1)
        hidden_dim = self.zoneout_cell.base_cell.hidden_size

        h = torch.zeros(batch_size, hidden_dim).to(x.device)  # 隠れ状態
        c = torch.zeros(batch_size, hidden_dim).to(x.device)  # セル状態（LSTMの場合）

        for t in range(seq_len):
            h, c = self.zoneout_cell(x[:, t, :], (h, c))  # Zoneoutを適用
        output = self.fc(h)
        return output

モデルのインスタンス化

model = ZoneoutRNNModel(input_dim=32, hidden_dim=128, output_dim=10, zoneout_prob=0.1)

損失関数とオプティマイザの設定

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

ダミーデータの生成

inputs = torch.randn(64, 10, 32)  # バッチサイズ64、シーケンス長10、入力次元32
targets = torch.randint(0, 10, (64,))  # 10クラス分類

トレーニングループ

for epoch in range(10):
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, targets)
    loss.backward()
    optimizer.step()

    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")
Epoch 1, Loss: 2.3051
Epoch 2, Loss: 2.2926
…
Epoch 9, Loss: 2.2040
Epoch 10, Loss: 2.1882

学習プロセスの制御と改善

学習プロセスの制御と改善とは、モデルの学習プロセスにおいて効率的かつ効果的に最適化を行い、モデル性能を向上させる技術や手法を指します。

  • 効率性の向上
    • 計算資源やメモリコストを削減しながら、同等またはより高い性能を達成。
  • 軽量化
    • 大規模モデルを小規模化し、デバイス間の転送やエッジデバイスでの使用を可能に。
  • 汎化性能の向上
    • 過学習を防ぎ、未知のデータに対する予測性能を向上させる。

蒸留

蒸留（Knowledge Distillation）は、これらの目標を達成するために活用される代表的な手法で、大規模なティーチャーモデル（教師モデル）の知識を、小規模なスチューデントモデル（生徒モデル）に効率よく転移する技術です。

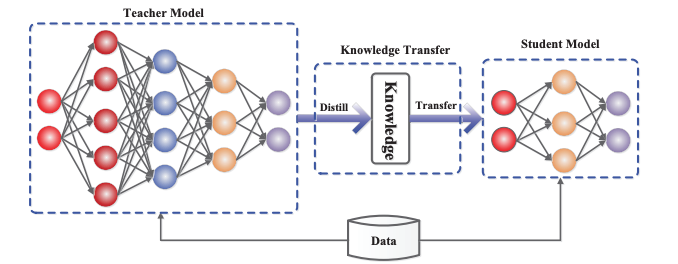
図1 知識抽出のための一般的な教師と生徒のフレームワーク。https://arxiv.org/pdf/2006.05525 より抜粋

特徴：

  • 大規模モデル（ティーチャーモデル）が持つ知識を転移することで、小規模モデルの性能を向上。
  • 軽量化されたモデルでも、大規模モデルに近い性能を発揮。
  • 主に、ティーチャーモデルとスチューデントモデルの出力を近づける形で学習。

数式：

  • 蒸留アルゴリズムは、通常のクロスエントロピー損失と、ティーチャーとスチューデントの出力分布を近づける損失（KLダイバージェンス）の加重和として定義されます。

$$L_{\text{distill}} = \alpha L_{\text{CE}}(S(x), y) + (1 – \alpha) L_{\text{KL}}(S(x), T(x))$$

  • $L_{\text{CE}}(S(x), y)$：スチューデントモデルの出力と正解ラベル $y$ のクロスエントロピー損失。
  • $L_{\text{KL}}(S(x), T(x))$：スチューデントモデルの出力 $S(x)$ とティーチャーモデルの出力 $T(x)$ のKLダイバージェンス。
  • $α$：ハイパーパラメータ（クロスエントロピー損失とKLダイバージェンスの比重を調整）。
  • $T$：温度スケーリング（ティーチャーモデルの出力分布をスムーズにするためのスケール）。
  • KLダイバージェンス

$$L_{\text{KL}} = T^2 \cdot \sum p_i \log \left( \frac{p_i}{q_i} \right)$$

  • 温度付きソフトマックス法
    • $p_i$​=softmax($T(x)/T$)：ティーチャーモデルのスムーズな出力分布。
    • $q_i$​=softmax($S(x)/T$)：スチューデントモデルのスムーズな出力分布。
  • 温度付きソフトマックス法とは？
    • 温度付きソフトマックス法は、出力分布のスムーズさを調整するために使用されるソフトマックス関数の拡張です。温度 $T$ によって出力の確率分布を制御し、$T > 1$ では分布をスムーズに、$T < 1$ では鋭くします。主に知識蒸留でティーチャーモデルの出力をスムーズ化し、生徒モデルが学習しやすい「ソフトターゲット」を生成する目的で使用されます。

$$p_i = \text{softmax}\left( \frac{x}{T} \right) = \frac{\exp(x_i / T)}{\sum_j \exp(x_j / T)}$$

  • $T>1$：出力分布が「スムーズ」になり、確率が均一化されます。
  • $T<1$：出力分布が「鋭く」なり、確率が一部の値に集中します。

蒸留アルゴリズムの蒸留損失関数の定義（PyTorch）：

次のコードは、知識蒸留における損失関数を定義しています。クロスエントロピー損失とKLダイバージェンス損失を組み合わせることで、生徒モデルの出力が教師モデルの出力に近づくようにします。これにより、生徒モデルが教師モデルの知識を効果的に学習し、より高い性能を発揮することが期待されます。

import torch.nn.functional as F

def distillation_loss(y_pred, y_true, teacher_pred, alpha=0.5, temperature=2):
    # クロスエントロピー損失
    loss_ce = F.cross_entropy(y_pred, y_true)
    
    # KLダイバージェンス損失
    loss_kl = F.kl_div(
        F.log_softmax(y_pred / temperature, dim=1),
        F.softmax(teacher_pred / temperature, dim=1),
        reduction='batchmean'
    ) * (temperature ** 2)
    
    # 全体の蒸留損失
    return alpha * loss_ce + (1 - alpha) * loss_kl

ニューラルネットワークで蒸留を使ってみる

ライブラリのインポート

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
from tqdm import tqdm  # プログレスバーの追加

教師モデルの定義

class TeacherNet(nn.Module):
    def __init__(self):
        super(TeacherNet, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.fc2 = nn.Linear(256, 256)
        self.fc3 = nn.Linear(256, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

生徒モデルの定義

class StudentNet(nn.Module):
    def __init__(self):
        super(StudentNet, self).__init__()
        self.fc1 = nn.Linear(784, 128)
        self.fc2 = nn.Linear(128, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

蒸留損失関数の定義

def distillation_loss(y_pred, y_true, teacher_pred, alpha=0.5, temperature=2):
    # クロスエントロピー損失
    loss_ce = F.cross_entropy(y_pred, y_true)
    
    # KLダイバージェンス損失
    loss_kl = F.kl_div(
        F.log_softmax(y_pred / temperature, dim=1),
        F.softmax(teacher_pred / temperature, dim=1),
        reduction='batchmean',
        log_target=True  # KLダイバージェンスの計算にlog_target=Trueを追加
    ) * (temperature ** 2)
    
    # 全体の蒸留損失
    return alpha * loss_ce + (1 - alpha) * loss_kl

データの準備

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))
])

train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)

test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=False)

モデルのインスタンス化

teacher_model = TeacherNet()
student_model = StudentNet()

デバイスの設定

device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
teacher_model.to(device)
student_model.to(device)

損失関数とオプティマイザの設定

optimizer = optim.Adam(student_model.parameters(), lr=0.001)

教師モデルのトレーニング

try:
    teacher_model.load_state_dict(torch.load('teacher_model.pth', map_location=device))  # 事前にトレーニング済みのモデルをロード
    print("Pre-trained teacher model loaded.")
except FileNotFoundError:
    print("Pre-trained teacher model not found. Please train the teacher model first.")
    # 教師モデルのトレーニングの例 (必要に応じて)
    teacher_optimizer = optim.Adam(teacher_model.parameters(), lr=0.001)
    num_epochs_teacher = 10
    for epoch in range(num_epochs_teacher):
        teacher_model.train()
        for data, target in tqdm(train_loader, desc=f"Training Teacher Model Epoch {epoch+1}/{num_epochs_teacher}"):
            data, target = data.to(device), target.to(device)
            teacher_optimizer.zero_grad()
            teacher_output = teacher_model(data.view(-1, 784))
            loss = F.cross_entropy(teacher_output, target)
            loss.backward()
            teacher_optimizer.step()
        print(f"Teacher Model Epoch {epoch+1}, Loss: {loss.item():.4f}")
    torch.save(teacher_model.state_dict(), 'teacher_model.pth')
    print("Teacher model trained and saved.")

事前にトレーニング済みの教師モデルをロードします。ファイルが見つからない場合は、教師モデルをトレーニングして保存します。

生徒モデルのトレーニング

num_epochs_student = 5
for epoch in range(num_epochs_student):
    student_model.train()
    total_loss = 0
    for data, target in tqdm(train_loader, desc=f"Training Student Model Epoch {epoch+1}/{num_epochs_student}"):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        student_output = student_model(data.view(-1, 784))
        with torch.no_grad():
            teacher_output = teacher_model(data.view(-1, 784))
        loss = distillation_loss(student_output, target, teacher_output)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    avg_loss = total_loss / len(train_loader)
    print(f"Epoch {epoch+1}, Average Loss: {avg_loss:.4f}")

生徒モデルの評価

student_model.eval()
correct = 0
total = 0
with torch.no_grad():
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        outputs = student_model(data.view(-1, 784))
        _, predicted = torch.max(outputs.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()

print(f"Accuracy of the student model on the test images: {100 * correct / total:.2f}%")
Accuracy of the student model on the test images: 97.26%

このコードのAccuracyは、生徒モデルがMNISTデータセットのテストデータに対してどれだけ正確に予測できるかを評価しています。具体的には、テストデータセットの各画像に対して生徒モデルが予測したクラスラベルが実際のクラスラベルと一致する割合を示しています。高い精度は、生徒モデルがテストデータに対して良好な性能を発揮していることを示します。

教師モデルの知識を生徒モデルに蒸留することで、生徒モデルが教師モデルの知識を効果的に学習し、より高い性能を発揮することが期待されます。

論文1

https://arxiv.org/pdf/2006.05525
arxiv.org
  • 知識蒸留の多様なアプローチ
    • 知識蒸留には、応答ベース、特徴量ベース、関係ベースの3つの主要な手法があります。これらはそれぞれ異なる視点で、教師モデルの知識を効率的に生徒モデルへ移す方法を提供します。本論文では、それぞれの手法の特徴や利点、さらに具体的な応用例を分かりやすく整理しています。
    • 応答ベースの強みと応用例
      • 応答ベースの手法では、教師モデルの出力（ロジット）の分布情報を生徒モデルに移します。これにより、生徒モデルは教師モデルの判断基準を効率的に学習できます。この方法は計算コストが低く、特に画像分類（CIFARデータセットなど）や自然言語処理といったタスクで、性能を大きく向上させることができます。Hintonらの研究から広く活用されています。

応答ベースの実装例：

応答ベースの手法では、教師モデルの出力（ロジット）を生徒モデルに移すことで、出力の分布情報を共有します。応答ベースの蒸留損失関数は、クロスエントロピー損失とKLダイバージェンス損失を組み合わせて、総合損失を計算します。つまり先ほど紹介したコードと同じです。

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets, transforms
from torch.utils.data import DataLoader

# 教師モデルの定義
class TeacherNet(nn.Module):
    def __init__(self):
        super(TeacherNet, self).__init__()
        self.fc1 = nn.Linear(784, 512)
        self.fc2 = nn.Linear(512, 512)
        self.fc3 = nn.Linear(512, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        output_logits = self.fc3(x)
        return output_logits

# 生徒モデルの定義
class StudentNet(nn.Module):
    def __init__(self):
        super(StudentNet, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.fc2 = nn.Linear(256, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        output_logits = self.fc2(x)
        return output_logits

# 応答ベースの蒸留損失関数
def response_based_loss(student_logits, teacher_logits, labels, alpha=0.5, temperature=2.0):
    teacher_probs = F.softmax(teacher_logits / temperature, dim=1)
    student_probs = F.softmax(student_logits / temperature, dim=1)
    distill_loss = F.kl_div(F.log_softmax(student_logits / temperature, dim=1), teacher_probs, reduction='batchmean') * (temperature ** 2)
    ce_loss = F.cross_entropy(student_logits, labels)
    return alpha * ce_loss + (1 - alpha) * distill_loss

# データの準備（MNISTデータセットを使用）
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=False)

# モデルのインスタンス化
teacher_model = TeacherNet()
student_model = StudentNet()
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
teacher_model.to(device)
student_model.to(device)

# 損失関数とオプティマイザ
teacher_optimizer = optim.Adam(teacher_model.parameters(), lr=0.001)
student_optimizer = optim.Adam(student_model.parameters(), lr=0.001)

# 教師モデルのトレーニング
num_epochs_teacher = 5
for epoch in range(num_epochs_teacher):
    teacher_model.train()
    for data, target in train_loader:
        data, target = data.to(device), target.to(device)
        teacher_optimizer.zero_grad()
        teacher_logits = teacher_model(data.view(-1, 784))
        loss = F.cross_entropy(teacher_logits, target)
        loss.backward()
        teacher_optimizer.step()

# 生徒モデルのトレーニング
num_epochs_student = 5
for epoch in range(num_epochs_student):
    student_model.train()
    for data, target in train_loader:
        data, target = data.to(device), target.to(device)
        student_optimizer.zero_grad()
        student_logits = student_model(data.view(-1, 784))
        with torch.no_grad():
            teacher_logits = teacher_model(data.view(-1, 784))
        loss = response_based_loss(student_logits, teacher_logits, target)
        loss.backward()
        student_optimizer.step()

# 生徒モデルの評価
student_model.eval()
correct = 0
total = 0
with torch.no_grad():
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        student_logits = student_model(data.view(-1, 784))
        _, predicted = torch.max(student_logits.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()
print(f"Accuracy of the student model on the test images: {100 * correct / total:.2f}%")
Accuracy of the student model on the test images: 97.40%
  • 特徴量ベースの強みと応用例
    • 特徴量ベースの手法は、教師モデルの中間層で生成される特徴マップを生徒モデルに移すことで、教師モデルが持つ豊富な内部表現を学習できます。この方法は、特に物体検出や画像分類のように深い特徴の活用が重要なタスクで効果を発揮します。教師モデルの高度な表現力を効率的に引き継ぐ点が大きな強みです。

特徴量ベースの実装：

特徴量ベースの手法では、教師モデルの中間層で生成される特徴マップを活用して、生徒モデルに内部表現を転送します。特徴量ベースの蒸留損失関数は、クロスエントロピー損失と特徴量のMSE損失を組み合わせて、総合損失を計算します。生徒モデルは中間層の出力次元を教師モデルの特徴次元（512）に合わせています。

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets, transforms
from torch.utils.data import DataLoader

# 教師モデルの定義
class TeacherNet(nn.Module):
    def __init__(self):
        super(TeacherNet, self).__init__()
        self.fc1 = nn.Linear(784, 512)
        self.fc2 = nn.Linear(512, 512)
        self.fc3 = nn.Linear(512, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        intermediate_features = F.relu(self.fc2(x))
        output_logits = self.fc3(intermediate_features)
        return output_logits, intermediate_features

# 生徒モデルの定義
class StudentNet(nn.Module):
    def __init__(self):
        super(StudentNet, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.fc2 = nn.Linear(256, 512)  # 出力次元を教師モデルの特徴次元に合わせる
        self.fc3 = nn.Linear(512, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        intermediate_features = F.relu(self.fc2(x))
        output_logits = self.fc3(intermediate_features)
        return output_logits, intermediate_features

# 特徴量ベースの蒸留損失関数
def feature_based_loss(student_logits, teacher_logits, student_features, teacher_features, labels, alpha=0.5, beta=0.5):
    ce_loss = F.cross_entropy(student_logits, labels)
    feature_loss = F.mse_loss(student_features, teacher_features)
    return alpha * ce_loss + beta * feature_loss

# データの準備（MNISTデータセットを使用）
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=False)

# モデルのインスタンス化
teacher_model = TeacherNet()
student_model = StudentNet()
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
teacher_model.to(device)
student_model.to(device)

# 損失関数とオプティマイザ
teacher_optimizer = optim.Adam(teacher_model.parameters(), lr=0.001)
student_optimizer = optim.Adam(student_model.parameters(), lr=0.001)

# 教師モデルのトレーニング
num_epochs_teacher = 5
for epoch in range(num_epochs_teacher):
    teacher_model.train()
    for data, target in train_loader:
        data, target = data.to(device), target.to(device)
        teacher_optimizer.zero_grad()
        teacher_logits, _ = teacher_model(data.view(-1, 784))
        loss = F.cross_entropy(teacher_logits, target)
        loss.backward()
        teacher_optimizer.step()

# 生徒モデルのトレーニング
num_epochs_student = 5
for epoch in range(num_epochs_student):
    student_model.train()
    for data, target in train_loader:
        data, target = data.to(device), target.to(device)
        student_optimizer.zero_grad()
        student_logits, student_features = student_model(data.view(-1, 784))
        with torch.no_grad():
            teacher_logits, teacher_features = teacher_model(data.view(-1, 784))
        loss = feature_based_loss(student_logits, teacher_logits, student_features, teacher_features, target)
        loss.backward()
        student_optimizer.step()

# 生徒モデルの評価
student_model.eval()
correct = 0
total = 0
with torch.no_grad():
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        student_logits, _ = student_model(data.view(-1, 784))
        _, predicted = torch.max(student_logits.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()
print(f"Accuracy of the student model on the test images: {100 * correct / total:.2f}%")
Accuracy of the student model on the test images: 98.13%
  • 関係ベースの強みと応用例
    • 関係ベースの手法は、データ間の関係性や特徴の相互作用をモデル化し、それを生徒モデルに移す方法です。この手法により、生徒モデルはデータの構造や特徴同士の依存関係を正確に学習できます。特に、顔認識や人物再識別など、データ間の関係性が重要なタスクで高い効果が確認されています。

関係ベースの実装例：

関係ベースの手法では、データ間の関係性や特徴の相互作用をモデル化し、生徒モデルに転送します。

関係ベースの蒸留損失関数は、クロスエントロピー損失と特徴量の関係性のMSE損失を組み合わせて、総合損失を計算します。生徒モデルは中間層の出力次元を教師モデルの特徴次元に合わせています。

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets, transforms
from torch.utils.data import DataLoader

# 教師モデルの定義
class TeacherNet(nn.Module):
    def __init__(self):
        super(TeacherNet, self).__init__()
        self.fc1 = nn.Linear(784, 512)
        self.fc2 = nn.Linear(512, 512)
        self.fc3 = nn.Linear(512, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        intermediate_features = F.relu(self.fc2(x))
        output_logits = self.fc3(intermediate_features)
        return output_logits, intermediate_features

# 生徒モデルの定義
class StudentNet(nn.Module):
    def __init__(self):
        super(StudentNet, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.fc2 = nn.Linear(256, 256)
        self.fc3 = nn.Linear(256, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        intermediate_features = F.relu(self.fc2(x))
        output_logits = self.fc3(intermediate_features)
        return output_logits, intermediate_features

# 関係ベースの蒸留損失関数
def relation_based_loss(student_logits, teacher_logits, student_features, teacher_features, labels, alpha=0.5, beta=0.5):
    ce_loss = F.cross_entropy(student_logits, labels)
    relation_loss = F.mse_loss(student_features @ student_features.T, teacher_features @ teacher_features.T)
    return alpha * ce_loss + beta * relation_loss

# データの準備（MNISTデータセットを使用）
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=False)

# モデルのインスタンス化
teacher_model = TeacherNet()
student_model = StudentNet()
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
teacher_model.to(device)
student_model.to(device)

# 損失関数とオプティマイザ
teacher_optimizer = optim.Adam(teacher_model.parameters(), lr=0.001)
student_optimizer = optim.Adam(student_model.parameters(), lr=0.001)

# 教師モデルのトレーニング
num_epochs_teacher = 5
for epoch in range(num_epochs_teacher):
    teacher_model.train()
    for data, target in train_loader:
        data, target = data.to(device), target.to(device)
        teacher_optimizer.zero_grad()
        teacher_logits, _ = teacher_model(data.view(-1, 784))
        loss = F.cross_entropy(teacher_logits, target)
        loss.backward()
        teacher_optimizer.step()

# 生徒モデルのトレーニング
num_epochs_student = 5
for epoch in range(num_epochs_student):
    student_model.train()
    for data, target in train_loader:
        data, target = data.to(device), target.to(device)
        student_optimizer.zero_grad()
        student_logits, student_features = student_model(data.view(-1, 784))
        with torch.no_grad():
            teacher_logits, teacher_features = teacher_model(data.view(-1, 784))
        loss = relation_based_loss(student_logits, teacher_logits, student_features, teacher_features, target)
        loss.backward()
        student_optimizer.step()

# 生徒モデルの評価
student_model.eval()
correct = 0
total = 0
with torch.no_grad():
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        student_logits, _ = student_model(data.view(-1, 784))
        _, predicted = torch.max(student_logits.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()
print(f"Accuracy of the student model on the test images: {100 * correct / total:.2f}%")
Accuracy of the student model on the test images: 97.63%

論文2：

Distilling the Knowledge in a Neural Network
A very simple way to improve the performance of almost any machine learning algorithm is to train many different models ...
arxiv.org
  • ディスティレーションの提案
    • 大規模なモデルやアンサンブルモデルの知識を、小型で効率的なモデルに転送する「ディスティレーション」という手法を提案しました。この手法では、ソフトターゲットを活用することで、小型モデルでも高い汎化性能を保ちながら、計算コストを大幅に削減できます。
  • ソフトターゲットの有効性
    • ディスティレーションでは、正解だけでなく、他クラスとの微妙な関係性も含む「ソフトターゲット」を活用します。これにより、小型モデルは少量のデータでも高い性能を発揮でき、過学習を防ぐ効果も得られます。
  • 実験での効果検証
    • MNISTや音声認識タスクで、小型モデルがアンサンブルモデルの80%以上の性能を実現することを確認しました。また、専門家モデルを用いたJFTデータセットの実験では、テスト精度が4.4%向上し、大規模データにも適用可能であることを示しました。

蒸留の派生アルゴリズムと類似法

FitNets

FitNetsは、ティーチャーモデルの中間層の特徴マップをスチューデントモデルに転移することで、軽量化されたスチューデントモデルの性能を大幅に向上させる手法です。


リグレッサーによる特徴次元の一致、ヒント損失の導入がその特徴であり、特に深いモデルや複雑なタスクで有効です。これにより、スチューデントモデルがティーチャーモデルの深い知識を学習しやすくなり、モデルの軽量化や汎化性能の向上を達成します。

数式やコードを通じてそのアルゴリズムを理解し、適切な場面で活用することで、効率的な知識転移を実現できます。

数式：

  • 通常の蒸留
    • 通常の蒸留では、ティーチャーモデル $T(x)$ とスチューデントモデル $S(x)$ の出力を一致させる形で学習します。

$$L_{\text{distill}} = \alpha L_{\text{CE}}(S(x), y) + (1 – \alpha) L_{\text{KL}}(S(x), T(x))$$

  • FitNetsの特徴転移
    • FitNetsでは、中間層の特徴マップ $F_T(x)$ と $F_S(x)$ の一致を目的とする損失を導入します。具体的には、次のような損失関数を定義します。

特徴マップの整合性損失

$$L_{\text{hint}} = \left\lVert g(F_T(x)) – F_S(x) \right\rVert^2$$

  • $F_T​(x)$：ティーチャーモデルの中間層の特徴マップ。
  • $F_S​(x)$：スチューデントモデルの中間層の特徴マップ。
  • $g$：ティーチャーとスチューデントの特徴次元を一致させる線形マッピング（リグレッサー）。

総合損失

$$L_{\text{FitNets}} = \beta L_{\text{hint}} + \gamma L_{\text{distill}}$$

  • $β、γ$：ハイパーパラメータ（ヒント損失と蒸留損失の重み付け）。

FitNetsのメリットとデメリット

メリット詳細
深いティーチャーモデルからの効果的な知識転移中間層の特徴マップを転移することで、スチューデントモデルがより深い知識を学習可能に。
スチューデントモデルの性能向上小規模なスチューデントモデルでも、ティーチャーモデルに近い性能を発揮し、高い効率でデプロイ可能にする。
デメリット詳細
計算コストの増加中間層の特徴マップを処理するため、ティーチャーモデルとスチューデントモデル間の追加計算が必要になる。
リグレッサーの設計依存特徴次元を一致させるためのリグレッサー設計が必要であり、不適切な設計は蒸留効果を低下させる可能性がある。

適用例：

適用例詳細
画像認識CNNを使用した画像分類タスクで、スチューデントモデルの性能向上に活用。
転移学習ティーチャーモデルを事前学習済みモデルとし、スチューデントモデルに知識を転移。
エッジデバイス向けモデルの軽量化モバイルやIoTデバイスでの使用を想定した、小型で高性能なスチューデントモデルの学習に適用。

FitNetsのの蒸留損失関数の定義（PyTorch）：

このコードは、FitNetsの蒸留損失を定義しています。通常の蒸留では、クロスエントロピー損失とKLダイバージェンス損失を組み合わせて、生徒モデルが教師モデルの出力に近づくようにします。一方、FitNetsでは、これに加えてヒント損失を導入し、教師モデルの中間層の特徴を生徒モデルの中間層の特徴に合わせることで、より深い層の知識を蒸留します。ヒント損失は、回帰器を通して教師モデルの特徴を生徒モデルの特徴に合わせるため、より詳細な知識の伝達が可能です。

import torch.nn.functional as F

def fitnets_loss(y_pred, y_true, teacher_pred, student_features, teacher_features, regressor, alpha=0.5, beta=0.5, temperature=2):
    # クロスエントロピー損失
    loss_ce = F.cross_entropy(y_pred, y_true)
    
    # KLダイバージェンス損失
    loss_kl = F.kl_div(
        F.log_softmax(y_pred / temperature, dim=1),
        F.softmax(teacher_pred / temperature, dim=1),
        reduction='batchmean'
    ) * (temperature ** 2)
    
    # ヒント損失
    teacher_features = regressor(teacher_features)
    loss_hint = F.mse_loss(student_features, teacher_features)
    
    # 全体の蒸留損失
    return alpha * loss_ce + (1 - alpha) * loss_kl + beta * loss_hint

厳密には上のコードは「FitNets」のアルゴリズムであるヒント損失に焦点を当てていますが、クロスエントロピー損失とKLダイバージェンス損失を組み合わせることで、より強力な蒸留が可能になります。この組み合わせは、「FitNets」の拡張版と考えることができます。

論文：

FitNets: Hints for Thin Deep Nets
While depth tends to improve network performances, it also makes gradient-based training more difficult since deeper net...
arxiv.org
  • ヒント」を活用した新しい訓練手法の提案
    • FitNetsは、教師ネットワークの中間層の出力を「ヒント」として活用することで、生徒ネットワークを効率よく訓練します。この方法により、薄くて深いネットワークでも高い性能を維持しつつ、計算コストを大幅に削減できます。
  • 2段階の訓練プロセスで効率的な知識転送を実現
    • FitNetsは、学生ネットワークを教師のヒント層を模倣するように訓練し、その後、分類タスクで微調整する2段階のプロセスを採用。この手法により、モデルの収束が安定し、性能が大幅に向上しました。
  • 実験で示された高い汎化性能
    • FitNetsは、CIFAR-10で教師モデルの10分の1のパラメータで性能を上回り、MNISTやSVHNでも優れた結果を達成しました。「ヒント」を活用することで、浅く幅広いモデルに匹敵する汎化性能を実現しています。

Attention Transfer (AT)

Attention Transfer（AT）は、ティーチャーモデルが入力に対して注目する領域（注意マップ）をスチューデントモデルに伝えることで、スチューデントモデルの学習効率を向上させる技術です。

この手法では、ティーチャーモデルとスチューデントモデルの注意領域の類似性を強調することで、スチューデントモデルの性能を向上させます。

数式やコードを通じてその仕組みを理解し、特にCNNベースのタスクにおいて適切に利用することで、モデル性能の向上が期待できます。

数式：

  • 注意マップの定義
    • 注意マップは、CNNの中間層出力の正規化された $L_2$​ ノルムとして定義されます。中間層の出力テンソルを $F \in \mathbb{R}^{C \times H \times W}$ とした場合

$$A(F) = \frac{1}{C} \sum_{c=1}^{C} F_{c,:,:}^2 \quad \in \mathbb{R}^{H \times W}$$

  • $F$ は中間層の出力テンソル。
  • $C,H,W$ はそれぞれチャンネル数、高さ、幅。
  • $A(F)$ は、正規化された注意マップ。
  • 注意マップの損失関数
    • ティーチャーモデルの注意マップ $A_T$​ とスチューデントモデルの注意マップ $A_S$​ を比較するために、損失関数が定義されます。

$$L_{\text{AT}} = \left\| A(F_T) – A(F_S) \right\|_F^2$$

  • $F_T$​：ティーチャーモデルの中間層出力。
  • $F_S$​：スチューデントモデルの中間層出力。
  • $\left|・ \right|_F^2$​：フロベニウスノルム（二乗和）。
  • 総合損失関数
    • 最終的な損失関数は、Attention Transfer の損失とクロスエントロピー損失の加重和として定義されます。

$$L = \alpha L_{\text{CE}}(S(x), y) + \beta L_{\text{AT}}$$

  • $α,β$ はハイパーパラメータ。
  • $\alpha L_{\text{CE}}(S(x), y)$はスチューデントモデルの出力と正解ラベル $y$ のクロスエントロピー損失。

Attention Transfer のメリットとデメリット

メリット説明
効率的な知識転移モデルの「注意」に焦点を当てることで、スチューデントモデルがティーチャーモデルの重要な領域を学習可能。
モデルサイズに依存しないティーチャーモデルとスチューデントモデルが異なる構造やサイズでも使用可能。
適用の柔軟性主にCNNベースのタスク（画像分類やセグメンテーションなど）で利用。
デメリット説明
計算コストの増加中間層の注意マップ計算と損失計算に追加の計算負荷がかかる。
実装の複雑さモデル内部の中間層出力にアクセスする必要があり、実装がより複雑になる。

適用例：

適用例説明
画像認識ResNetやVGGなどのCNNモデルで、スチューデントモデルの精度向上に活用。
セグメンテーション注意マップがピクセル単位での領域を示すため、セグメンテーションタスクに有効。
転移学習高度に学習されたティーチャーモデルから小型モデルへ知識を転移する際に利用可能。

Attention Transferの蒸留損失関数の定義（PyTorch）：

import torch.nn.functional as F

def attention_transfer_loss(y_pred, y_true, teacher_pred, student_attention, teacher_attention, alpha=0.5, beta=0.5, temperature=2):
    # クロスエントロピー損失
    loss_ce = F.cross_entropy(y_pred, y_true)
    
    # KLダイバージェンス損失
    loss_kl = F.kl_div(
        F.log_softmax(y_pred / temperature, dim=1),
        F.softmax(teacher_pred / temperature, dim=1),
        reduction='batchmean'
    ) * (temperature ** 2)
    
    # Attention Transfer損失
    def attention_map(features):
        return F.normalize(features.pow(2).mean(1).view(features.size(0), -1))

    student_attention_map = attention_map(student_attention)
    teacher_attention_map = attention_map(teacher_attention)
    loss_at = F.mse_loss(student_attention_map, teacher_attention_map)
    
    # 全体の蒸留損失
    return alpha * loss_ce + (1 - alpha) * loss_kl + beta * loss_at

論文：

Paying More Attention to Attention: Improving the Performance of Convolutional Neural Networks via Attention Transfer
Attention plays a critical role in human visual experience. Furthermore, it has recently been demonstrated that attentio...
arxiv.org
  • 注意マップを活用した知識転送の提案
    • 本論文では、教師ネットワークの注意マップ（活性化ベースおよび勾配ベース）を生徒ネットワークが模倣する「注意転送」を提案。これにより、生徒ネットワークは高い性能と効率的な学習を実現します。
  • 注意転送の実験的な有効性の証明
    • CIFAR-10やImageNetでの実験により、注意転送が分類性能を一貫して向上させることを確認。特に、活性化ベースの注意転送はフルアクティベーション転送よりも優れた結果を示しました。
  • 幅広い応用可能性と効率性
    • 注意転送は、教師から生徒への知識蒸留と組み合わせることでさらなる性能向上を実現。また、計算コストをほとんど増加させず、さまざまなデータセットやアーキテクチャに適用可能であることが示されました。

Soft Targets

Soft Targets は、通常のクロスエントロピー損失では学習できないティーチャーモデルのソフトな出力分布を利用することで、スチューデントモデルがより豊かな情報を学習できるようにする手法です。

ティーチャーモデルの出力分布には、単純な正解ラベル（ハードターゲット）では得られないクラス間の相対的な関係が含まれています。
この情報を活用することで、スチューデントモデルはティーチャーモデルの知識を効果的に引き継ぎ、汎化性能を向上させます。

数式やコードを通じてその動作を理解することで、さまざまなモデルの軽量化や汎化性能向上に役立てることができます。

数式：

  • ソフトターゲットの定義
    • ティーチャーモデルの出力を $z_T$ とし、温度 $T$ を用いて次のように「ソフトな確率分布」を生成します。

$$p_T(i) = \frac{\exp(z_{T,i} / T)}{\sum_j \exp(z_{T,j} / T)}$$

  • $p_T​(i)$：ティーチャーモデルのソフトターゲット確率（クラス $i$ の確率）。
  • $z_T$, $i$​：ティーチャーモデルのクラス $i$ の生出力（logits）。
  • $T$：温度（高い値にすると分布が平滑化される）。
  • 蒸留損失
    • Soft Targets を利用した損失関数は、通常のクロスエントロピー損失と、ソフトターゲットのKLダイバージェンスを組み合わせて定義されます。

$$L_{\text{distill}} = \alpha L_{\text{CE}}(S(x), y) + (1 – \alpha)T^2 \cdot L_{\text{KL}}(p_S, p_T)$$

  • $\alpha L_{\text{CE}}(S(x), y)$：スチューデントモデルの出力と正解ラベルのクロスエントロピー損失。
  • $\cdot L_{\text{KL}}(p_S, p_T)$：スチューデントモデルのソフトターゲット分布$p_S​$とティーチャーモデルのソフトターゲット分布 $p_T$​ のKLダイバージェンス。
  • $α$：クロスエントロピーとKL損失の重みを調整するハイパーパラメータ。

Soft Targets のメリットとデメリット

メリット説明
ティーチャーモデルの知識を効果的に転移クラス間の相対的な関係を含むソフトな分布をスチューデントモデルが学習可能。
汎化性能の向上スチューデントモデルがティーチャーモデルを通じて幅広いデータ分布に対応できる。
柔軟性ティーチャーとスチューデントモデルのサイズや構造が異なっていても適用可能。
デメリット説明
計算コストの増加温度スケーリングや分布比較の計算に追加の計算負荷が発生する。
温度や α の調整が必要モデルやタスクに応じて温度パラメータや α の適切な設定が求められ、試行錯誤が必要になる。

適用例：

適用例説明
大規模モデルの軽量化大規模なティーチャーモデルから軽量なスチューデントモデルへの知識転移（例：BERT→DistilBERT）。
画像認識タスク大規模なResNetモデルから小規模なMobileNetモデルへの蒸留。
自然言語処理GPTやBERTなどの知識を小型のスチューデントモデルに転移し、性能を維持しつつモデルを軽量化する。

Soft Targetsの蒸留損失関数の定義（PyTorch）：

このコードは、Soft Targetsの蒸留損失を使用して生徒モデルをトレーニングするものです。Soft Targetsの蒸留損失（soft_targets_loss 関数）は、クロスエントロピー損失とKLダイバージェンス損失を組み合わせて計算されます。

import torch
import torch.nn.functional as F

def soft_targets_loss(y_pred, y_true, teacher_pred, alpha=0.5, temperature=2):
    # クロスエントロピー損失
    loss_ce = F.cross_entropy(y_pred, y_true)
    
    # KLダイバージェンス損失
    loss_kl = F.kl_div(
        F.log_softmax(y_pred / temperature, dim=1),
        F.softmax(teacher_pred / temperature, dim=1),
        reduction='batchmean'
    ) * (temperature ** 2)
    
    # 全体の蒸留損失
    return alpha * loss_ce + (1 - alpha) * loss_kl

# 使用例
student_output = torch.randn(10, 5)  # 生徒モデルの出力例
teacher_output = torch.randn(10, 5)  # 教師モデルの出力例
true_labels = torch.randint(0, 5, (10,))  # 真のラベルの例

loss = soft_targets_loss(student_output, true_labels, teacher_output)
print(loss)
  • soft_targets_loss 関数は、真のラベルとのクロスエントロピー損失と教師モデルの出力とのKLダイバージェンス損失を組み合わせて、全体の蒸留損失を計算します。この組み合わせた損失は、生徒モデルが真のラベルと教師モデルの出力分布の両方から学習するのを助けます。
  • Soft Targetsは通常の蒸留と同じアプローチを取ります。具体的には、教師モデルのソフトターゲットモデルの出力を生徒モデルに転送することで、より効果的な知識蒸留を実現します。以下はその具体的なコーディング例です。

ライブラリのインポート

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
from tqdm import tqdm

教師モデルの定義

class TeacherNet(nn.Module):
    def __init__(self):
        super(TeacherNet, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.fc2 = nn.Linear(256, 256)
        self.fc3 = nn.Linear(256, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

教師モデル（TeacherNet）は、3つの全結合層（fully connected layers）を持つシンプルなニューラルネットワークです。

生徒モデルの定義

class StudentNet(nn.Module):
    def __init__(self):
        super(StudentNet, self).__init__()
        self.fc1 = nn.Linear(784, 128)
        self.fc2 = nn.Linear(128, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

生徒モデル（StudentNet）は、2つの全結合層を持つシンプルなニューラルネットワークです。

データの準備

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))
])

train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)

test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=False)

モデルのインスタンス化とデバイスの設定

teacher_model = TeacherNet()
student_model = StudentNet()

device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
teacher_model.to(device)
student_model.to(device)

損失関数とオプティマイザの設定

optimizer = optim.Adam(student_model.parameters(), lr=0.001)

生徒モデルのパラメータを最適化するためのAdamオプティマイザを設定します。

教師モデルのトレーニング

try:
    teacher_model.load_state_dict(torch.load('teacher_model.pth', map_location=device))
    print("Pre-trained teacher model loaded.")
except FileNotFoundError:
    print("Pre-trained teacher model not found. Please train the teacher model first.")
    teacher_optimizer = optim.Adam(teacher_model.parameters(), lr=0.001)
    num_epochs_teacher = 10
    for epoch in range(num_epochs_teacher):
        teacher_model.train()
        for data, target in tqdm(train_loader, desc=f"Training Teacher Model Epoch {epoch+1}/{num_epochs_teacher}"):
            data, target = data.to(device), target.to(device)
            teacher_optimizer.zero_grad()
            teacher_output = teacher_model(data.view(-1, 784))
            loss = F.cross_entropy(teacher_output, target)
            loss.backward()
            teacher_optimizer.step()
        print(f"Teacher Model Epoch {epoch+1}, Loss: {loss.item():.4f}")
    torch.save(teacher_model.state_dict(), 'teacher_model.pth')
    print("Teacher model trained and saved.")

事前にトレーニング済みの教師モデルをロードします。ファイルが見つからない場合は、教師モデルをトレーニングして保存します。

Soft Targetsの蒸留損失関数の定義

def soft_targets_loss(y_pred, y_true, teacher_pred, alpha=0.5, temperature=2):
    loss_ce = F.cross_entropy(y_pred, y_true)
    loss_kl = F.kl_div(
        F.log_softmax(y_pred / temperature, dim=1),
        F.softmax(teacher_pred / temperature, dim=1),
        reduction='batchmean'
    ) * (temperature ** 2)
    return alpha * loss_ce + (1 - alpha) * loss_kl

クロスエントロピー損失とKLダイバージェンス損失を組み合わせて、全体の蒸留損失を計算する関数を定義します。

生徒モデルのトレーニング

num_epochs_student = 5
for epoch in range(num_epochs_student):
    student_model.train()
    total_loss = 0
    for data, target in tqdm(train_loader, desc=f"Training Student Model Epoch {epoch+1}/{num_epochs_student}"):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        student_output = student_model(data.view(-1, 784))
        with torch.no_grad():
            teacher_output = teacher_model(data.view(-1, 784))
        loss = soft_targets_loss(student_output, target, teacher_output)
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    avg_loss = total_loss / len(train_loader)
    print(f"Epoch {epoch+1}, Average Loss: {avg_loss:.4f}")

各エポックで生徒モデルをトレーニングします。生徒モデルの出力と教師モデルの出力を使用して蒸留損失を計算し、バックプロパゲーションとパラメータ更新を行います。

生徒モデルの評価

student_model.eval()
correct = 0
total = 0
with torch.no_grad():
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        outputs = student_model(data.view(-1, 784))
        _, predicted = torch.max(outputs.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()
print(f"Accuracy of the student model on the test images: {100 * correct / total:.2f}%")

テストデータを使用して生徒モデルの精度を評価します。評価結果は通常の蒸留よりも精度が上がっています。

論文：

https://arxiv.org/pdf/1503.02531
arxiv.org
  • Soft Targetsの役割
    • Soft Targetsは、モデルが出力する確率分布を利用して、大きなモデルの知識を小さなモデルに伝える手法です。正解ラベルだけでなく、クラス間の関係性を含んだ豊かな情報を学習できるため、小さなモデルでも効率よく高い性能を発揮できます。
  • 温度パラメータの重要性
    • 温度パラメータ $T$ をSoftmax関数に加えると、出力の確率分布が滑らか（ソフト）になります。温度を高くするとクラス間の確率の差が小さくなり、モデルは微妙な関係性も学習できるようになります。これにより、学習が安定し、モデルの一般化性能が向上します。
  • 正則化効果と一般化
    • Soft Targetsは、過学習を防ぐ正則化の役割を果たします。少ないデータでも学習が安定し、自然に収束するため、高い精度が得られます。実際にMNISTデータセットでは、早期停止せず精度が向上することが確認されています。

RKD

RKD（Relational Knowledge Distillation）は、通常の蒸留が個々の出力（確率分布）に焦点を当てるのに対し、モデルの出力間の関係性（距離や角度）をスチューデントモデルに転移する手法です。これにより、ティーチャーモデルの相対的な知識をスチューデントモデルが学習でき、より柔軟な知識転移が可能になります。

数式：

  • 距離ベースの関係性
    • ティーチャーモデルとスチューデントモデルの出力間の距離関係を利用します。ティーチャーとスチューデントの出力をそれぞれ $T$（ティーチャーモデル）と $S$（スチューデントモデル）とした場合。

$$d_T(i, j) = \|T_i – T_j\|_2 \\$$
$$d_S(i, j) = \|S_i – S_j\|_2$$

  • $d_T​(i,j)$：ティーチャーモデルの出力間の距離。
  • $d_S​(i,j)$：スチューデントモデルの出力間の距離。
  • $∥⋅∥_2​$：L2ノルム（ユークリッド距離）。
  • 角度ベースの関係性
    • モデルの出力間の角度関係を利用する場合

$$a_T(i, j) = \cos^{-1} \left( \frac{(T_i – T_j) \cdot (T_k – T_j)}{\|T_i – T_j\|_2 \|T_k – T_j\|_2} \right)$$

$$a_S(i, j) = \cos^{-1} \left( \frac{(S_i – S_j) \cdot (S_k – S_j)}{\|S_i – S_j\|_2 \|S_k – S_j\|_2} \right)$$

  • $a_T​(i,j)$：ティーチャーモデルの出力間の角度。
  • $a_S​(i,j)$：スチューデントモデルの出力間の角度。
  • RKDの損失関数
    • RKDでは、ティーチャーとスチューデント間の関係性を距離と角度を用いて一致させる損失を定義します。

$$L_{RKD} = \alpha \sum_{i,j} \|d_T(i, j) – d_S(i, j)\|_2^2 + \beta \sum_{i,j,k} \|a_T(i, j, k) – a_S(i, j, k)\|_2^2$$

  • $α,β$：距離損失と角度損失の重みを調整するハイパーパラメータ。

RKDのメリットとデメリット

メリット詳細
柔軟な知識転移個々の出力ではなく、クラス間の相対的な関係を転移。
汎化性能の向上クラスの相互関係を学習することで、スチューデントモデルの一般化能力が向上。
適用範囲の広さティーチャーとスチューデントモデルが異なるアーキテクチャでも利用可能。
デメリット詳細
計算コストの増加出力間の距離や角度を計算するため、計算コストが高くなる。
パラメータの調整が必要距離損失と角度損失のバランスを取るためのハイパーパラメータ $α,β$ の調整が必要。

適用例：

タスク詳細
画像認識タスクResNetのようなCNNを用いた画像分類タスク。
自然言語処理文の類似性や文間関係の学習を伴うNLPタスク。
転移学習大規模ティーチャーモデル（例：BERT）から小型スチューデントモデル（例：DistilBERT）への知識転移。

RKDの蒸留損失関数の定義（PyTorch）：

import torch.nn.functional as F

def rkd_loss(student_features, teacher_features, beta_distance=1.0, beta_angle=1.0):
    # RKD距離損失
    def pairwise_distances(x):
        dot_product = torch.matmul(x, x.t())
        square_norm = torch.diag(dot_product)
        distances = square_norm.unsqueeze(1) - 2 * dot_product + square_norm.unsqueeze(0)
        return distances

    student_distances = pairwise_distances(student_features)
    teacher_distances = pairwise_distances(teacher_features)
    loss_rkd_distance = F.mse_loss(student_distances, teacher_distances)
    
    # RKD角度損失
    def pairwise_angles(x):
        norm_x = F.normalize(x, p=2, dim=1)
        angles = torch.matmul(norm_x, norm_x.t())
        return angles

    student_angles = pairwise_angles(student_features)
    teacher_angles = pairwise_angles(teacher_features)
    loss_rkd_angle = F.mse_loss(student_angles, teacher_angles)
    
    # 全体のRKD損失
    return beta_distance * loss_rkd_distance + beta_angle * loss_rkd_angle

生徒モデルのトレーニング

num_epochs_student = 5
for epoch in range(num_epochs_student):
    student_model.train()
    total_loss = 0
    for data, target in tqdm(train_loader, desc=f"Training Student Model Epoch {epoch+1}/{num_epochs_student}"):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        
        # 生徒モデルの出力を計算
        student_output = student_model(data.view(-1, 784))
        
        # 教師モデルの出力を計算（勾配を計算しない）
        with torch.no_grad():
            teacher_output = teacher_model(data.view(-1, 784))
        
        # 生徒モデルの特徴を抽出
        student_features = student_model.fc1(data.view(-1, 784))
        
        # 教師モデルの特徴を抽出
        with torch.no_grad():
            teacher_features = teacher_model.fc2(F.relu(teacher_model.fc1(data.view(-1, 784))))
        
        # RKD損失を計算
        loss = rkd_loss(student_features, teacher_features)
        
        # バックプロパゲーションとパラメータ更新
        loss.backward()
        optimizer.step()
        
        total_loss += loss.item()
    avg_loss = total_loss / len(train_loader)
    print(f"Epoch {epoch+1}, Average Loss: {avg_loss:.4f}")

各エポックで生徒モデルをトレーニングします。生徒モデルの出力と教師モデルの特徴を使用してRKD損失を計算し、バックプロパゲーションとパラメータ更新を行います。

生徒モデルの評価

student_model.eval()
correct = 0
total = 0
with torch.no_grad():
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        outputs = student_model(data.view(-1, 784))
        _, predicted = torch.max(outputs.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()
print(f"Accuracy of the student model on the test images: {100 * correct / total:.2f}%")

RKD損失は、教師モデルと生徒モデルの特徴間の距離や角度の関係を一致させることで計算されます。このアプローチは、計算コストを抑えつつ、特徴間の関係性を学習することを目的としています。

論文：

Relational Knowledge Distillation
Knowledge distillation aims at transferring knowledge acquired in one model (a teacher) to another model (a student) tha...
arxiv.org
  • データ間の関係性を利用した新しい知識蒸留手法
    • RKDは、データ間の「関係性」に注目した新しい知識蒸留手法です。従来は教師モデルの出力そのものを模倣する方法が主流でしたが、RKDはデータ間の距離や角度といった構造的な情報を生徒モデルに伝えることで、特にメトリック学習の分野で、生徒モデルが教師モデルを超える性能を発揮しています。
      • メトリック学習とは？：
        メトリック学習とは、データ間の類似性や距離を学習する手法で、類似データを近づけ、異なるデータを離すよう埋め込み表現を最適化します。
  • 高次の関係性を活用する柔軟なフレームワーク
    • RKDは、データ間の距離や角度といった高次の関係性を活用する柔軟なフレームワークです。この手法は、従来の知識蒸留を補完しつつ一般化を図り、タスクに応じて柔軟に適応できる点が特長です。様々なタスクでその効果が実証されています。
  • 自己蒸留や他手法との組み合わせによる補完性
    • RKDは自己蒸留においても効果的であり、生徒モデルが教師モデルを上回る性能を実現します。また、従来の知識蒸留手法と組み合わせることでさらなる性能向上を図ることが可能で、幅広い応用が期待されています。

RKD（拡張版：従来の知識蒸留手法と組み合わせ）：

import torch.nn.functional as F

def combined_rkd_loss(y_pred, y_true, teacher_pred, student_features, teacher_features, alpha=0.5, beta_distance=1.0, beta_angle=1.0, temperature=2):
    # クロスエントロピー損失
    loss_ce = F.cross_entropy(y_pred, y_true)
    
    # KLダイバージェンス損失
    loss_kl = F.kl_div(
        F.log_softmax(y_pred / temperature, dim=1),
        F.softmax(teacher_pred / temperature, dim=1),
        reduction='batchmean'
    ) * (temperature ** 2)
    
    # RKD距離損失
    def pairwise_distances(x):
        dot_product = torch.matmul(x, x.t())
        square_norm = torch.diag(dot_product)
        distances = square_norm.unsqueeze(1) - 2 * dot_product + square_norm.unsqueeze(0)
        return distances

    student_distances = pairwise_distances(student_features)
    teacher_distances = pairwise_distances(teacher_features)
    loss_rkd_distance = F.mse_loss(student_distances, teacher_distances)
    
    # RKD角度損失
    def pairwise_angles(x):
        norm_x = F.normalize(x, p=2, dim=1)
        angles = torch.matmul(norm_x, norm_x.t())
        return angles

    student_angles = pairwise_angles(student_features)
    teacher_angles = pairwise_angles(teacher_features)
    loss_rkd_angle = F.mse_loss(student_angles, teacher_angles)
    
    # 全体の蒸留損失
    return alpha * (loss_ce + loss_kl) + beta_distance * loss_rkd_distance + beta_angle * loss_rkd_angle

CRD

CRD（Contrastive Representation Distillation）は、スチューデントモデルがティーチャーモデルと同じ表現空間を学習できるようにする手法です。コントラスト学習を応用することで、より深い知識の転移とスチューデントモデルの汎化性能向上を実現します。

数式やコードを通じてその仕組みを理解し、多様なタスクで効果的に活用することが可能です。

数式：

  • コントラスト損失の定義
    • CRDでは、ティーチャーの表現 $z_T$​ とスチューデントの表現 $z_S$​ の関係を「正例（Positive）」と「負例（Negative）」で区別し、情報量最大化の観点から損失を定義します。

$$L_{CRD} = -\log \frac{\exp(\text{sim}(z_T^i, z_S^i) / \tau)}{\sum_{j=1}^N \exp(\text{sim}(z_T^i, z_S^j) / \tau)}$$

  • $z_T^i$：ティーチャーモデルの表現空間における正例（クラス $i$）。
  • $z_S^i$：スチューデントモデルの表現空間における正例（クラス $i$）。
  • $\text{sim}(a,b)$：ベクトル $a$ と $b$ のコサイン類似度。
  • $τ$：温度スケール（スケーリング用のハイパーパラメータ）。
  • $N$：負例の総数（ミニバッチサイズ）。
  • コサイン類似度
    • コサイン類似度については詳しくは下記のブログ記事を参照して下さい。
【第8回】教師なし学習の基本とラベルなきデータの可能性【前編】
目的 このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用...
shion.blog
2024.11.03

$$\text{sim}(a, b) = \frac{a \cdot b}{\|a\| \|b\|}$$

CRDのメリットとデメリット

メリット詳細
高精度な表現転移単純な出力分布ではなく、表現間の類似性を転移することで、スチューデントモデルが深い知識を学習可能。
汎化性能の向上コントラスト学習を活用することで、スチューデントモデルの一般化能力が向上。
適用範囲の広さ画像分類、自然言語処理など、多様なタスクで有効。
デメリット詳細
計算コストの増加表現間のペアワイズ計算により、計算コストが高くなる。
温度スケールと負例数の調整が必要ハイパーパラメータの調整がタスクに応じて必要。

適用例：

適用例詳細
画像認識タスクCNNベースのモデル（ResNetやEfficientNet）の知識転移。
自然言語処理テキストの意味表現を扱うタスク（例：BERT→DistilBERT）。
転移学習大規模事前学習モデルから小型モデルへの効率的な知識転移。

CRDの蒸留損失関数の定義（PyTorch）：

import torch
import torch.nn.functional as F

def contrastive_loss(teacher_features, student_features, temperature=0.07):
    """
    CRD損失関数
    :param teacher_features: ティーチャーモデルの特徴表現 (B, D)
    :param student_features: スチューデントモデルの特徴表現 (B, D)
    :param temperature: 温度スケール
    :return: CRD損失
    """
    # 正規化（コサイン類似度計算のため）
    teacher_features = F.normalize(teacher_features, dim=1)
    student_features = F.normalize(student_features, dim=1)

    # コサイン類似度を計算
    similarity_matrix = torch.matmul(student_features, teacher_features.T) / temperature

    # 正例と負例の損失を計算
    positive_samples = torch.diag(similarity_matrix)  # 正例の類似度
    negative_samples = torch.sum(torch.exp(similarity_matrix), dim=1) - torch.exp(positive_samples)  # 負例の類似度

    # CRD損失を計算
    loss = -torch.mean(torch.log(torch.exp(positive_samples) / (negative_samples + torch.exp(positive_samples))))
    return loss

ライブラリをインポート

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
from tqdm import tqdm

教師モデルの定義

class TeacherNet(nn.Module):
    def __init__(self):
        super(TeacherNet, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.fc2 = nn.Linear(256, 256)
        self.fc3 = nn.Linear(256, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

生徒モデルの定義

class StudentNet(nn.Module):
    def __init__(self):
        super(StudentNet, self).__init__()
        self.fc1 = nn.Linear(784, 128)
        self.fc2 = nn.Linear(128, 256)  # 出力次元を教師モデルの特徴次元に合わせる
        self.fc3 = nn.Linear(256, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

CRD損失関数の定義

def contrastive_loss(teacher_features, student_features, temperature=0.07):
    """
    CRD損失関数
    :param teacher_features: ティーチャーモデルの特徴表現 (B, D)
    :param student_features: スチューデントモデルの特徴表現 (B, D)
    :param temperature: 温度スケール
    :return: CRD損失
    """
    # 正規化（コサイン類似度計算のため）
    teacher_features = F.normalize(teacher_features, dim=1)
    student_features = F.normalize(student_features, dim=1)

    # コサイン類似度を計算
    similarity_matrix = torch.matmul(student_features, teacher_features.T) / temperature

    # 正例と負例の損失を計算
    positive_samples = torch.diag(similarity_matrix)  # 正例の類似度
    negative_samples = torch.sum(torch.exp(similarity_matrix), dim=1) - torch.exp(positive_samples)  # 負例の類似度

    # CRD損失を計算
    loss = -torch.mean(torch.log(torch.exp(positive_samples) / (negative_samples + torch.exp(positive_samples))))
    return loss

データの準備

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))
])

train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)

test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=False)

モデルのインスタンス化とデバイスの設定

teacher_model = TeacherNet()
student_model = StudentNet()

device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
teacher_model.to(device)
student_model.to(device)

損失関数とオプティマイザの設定

optimizer = optim.Adam(student_model.parameters(), lr=0.001)

教師モデルのトレーニング

try:
    teacher_model.load_state_dict(torch.load('teacher_model.pth', map_location=device))
    print("Pre-trained teacher model loaded.")
except FileNotFoundError:
    print("Pre-trained teacher model not found. Please train the teacher model first.")
    teacher_optimizer = optim.Adam(teacher_model.parameters(), lr=0.001)
    num_epochs_teacher = 10
    for epoch in range(num_epochs_teacher):
        teacher_model.train()
        for data, target in tqdm(train_loader, desc=f"Training Teacher Model Epoch {epoch+1}/{num_epochs_teacher}"):
            data, target = data.to(device), target.to(device)
            teacher_optimizer.zero_grad()
            teacher_output = teacher_model(data.view(-1, 784))
            loss = F.cross_entropy(teacher_output, target)
            loss.backward()
            teacher_optimizer.step()
        print(f"Teacher Model Epoch {epoch+1}, Loss: {loss.item():.4f}")
    torch.save(teacher_model.state_dict(), 'teacher_model.pth')
    print("Teacher model trained and saved.")

生徒モデルのトレーニング

num_epochs_student = 5
for epoch in range(num_epochs_student):
    student_model.train()
    total_loss = 0
    for data, target in tqdm(train_loader, desc=f"Training Student Model Epoch {epoch+1}/{num_epochs_student}"):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        
        # 生徒モデルの出力を計算
        student_output = student_model(data.view(-1, 784))
        
        # 教師モデルの出力を計算（勾配を計算しない）
        with torch.no_grad():
            teacher_output = teacher_model(data.view(-1, 784))
        
        # 生徒モデルの特徴を抽出
        student_features = student_model.fc2(F.relu(student_model.fc1(data.view(-1, 784))))
        
        # 教師モデルの特徴を抽出
        with torch.no_grad():
            teacher_features = teacher_model.fc2(F.relu(teacher_model.fc1(data.view(-1, 784))))
        
        # クロスエントロピー損失を計算
        loss_ce = F.cross_entropy(student_output, target)
        
        # KLダイバージェンス損失を計算
        loss_kl = F.kl_div(
            F.log_softmax(student_output / 2.0, dim=1),
            F.softmax(teacher_output / 2.0, dim=1),
            reduction='batchmean'
        ) * (2.0 ** 2)
        
        # CRD損失を計算
        loss_crd = contrastive_loss(teacher_features, student_features)
        
        # 総損失を計算
        loss = loss_ce + loss_kl + loss_crd
        
        # バックプロパゲーションとパラメータ更新
        loss.backward()
        optimizer.step()
        
        total_loss += loss.item()
    avg_loss = total_loss / len(train_loader)
    print(f"Epoch {epoch+1}, Average Loss: {avg_loss:.4f}")

生徒モデルの評価

student_model.eval()
correct = 0
total = 0
with torch.no_grad():
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        outputs = student_model(data.view(-1, 784))
        _, predicted = torch.max(outputs.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()
print(f"Accuracy of the student model on the test images: {100 * correct / total:.2f}%")

論文：

Contrastive Representation Distillation
Often we wish to transfer representational knowledge from one neural network to another. Examples include distilling a l...
arxiv.org
  • CRDの革新性
    • CRDはコントラスト学習を用いて、教師と生徒の間で相互情報量を最大化し、高次の表現構造を学習させる新手法です。従来のKLダイバージェンスに依存するKDの欠点を克服しています。
  • 圧倒的な性能向上
    • CRDは従来の知識蒸留手法を全て上回り、特に教師モデルと異なるアーキテクチャ間での転移に強く、教師モデルの性能を超える場合もあります。平均57%の性能向上を達成しました。
  • 多様な応用可能性
    • CRDはモデル圧縮、クロスモーダル転移、アンサンブル蒸留など、多様なタスクに適用可能です。画像から深度や音声への表現転移など、異なるモダリティ間の転移でも成功しています。

Self-Distillation（自己蒸留）

Self-Distillation は、同じモデル内で知識を転移する手法です。つまりモデル内で自己学習を行う手法です。通常の知識蒸留では、大規模なティーチャーモデルから小規模なスチューデントモデルに知識を転移しますが、Self-Distillation ではモデル自身をティーチャーとして利用し、出力層の予測を中間層に伝えます。これにより、モデルの性能向上や汎化性能の向上が期待されます。

モデル内で自己学習を行う手法とは？

出力層と中間層の関係を強化することで、外部ティーチャーに頼らず、同じモデル内で知識を転移し、自己学習を行うことでモデル性能を向上させます。特に中間層を持つ深層モデルに適用することで、計算コストを抑えつつ汎化性能の向上が期待できます。

Self-Distillation（自己蒸留）は自己教師あり学習と呼べるか？

Self-Distillation は、自己教師あり学習と似た要素を持ちますが、通常は 「教師あり学習を補完する手法」 として使用されます。そのため、完全な自己教師あり学習と呼ぶのは適切ではありませんが、一部のケースでは自己教師あり学習に近い性質を持つと評価されることもあります。

数式：

Self-Distillation では、出力層の確率分布 $p_T$​ を中間層の特徴量 $h_i$​ を元に構成されたスチューデント分布 $p_S$​ に伝えるため、損失関数が以下のように定義されます。

  • 出力分布（ティーチャー）
    • Softmax関数を用いて、モデルの出力 $z_T$​ からティーチャーの確率分布を生成します。

$$p_T(i) = \frac{\exp(z_{T,i} / T)}{\sum_j \exp(z_{T,j} / T)}$$

  • $z_T$​：出力層のロジット。
  • $T$：温度パラメータ（平滑化のため）。
  • 中間層分布（スチューデント）
    • 中間層の特徴量 $h_i$​ を用いてスチューデントの出力分布を生成します。

$$ps(i) = \frac{\exp(h_i / T)}{\sum_j \exp(h_j / T)}$$

  • $h_i$​：中間層の特徴量。
  • Self-Distillation の損失関数
    • ティーチャーとスチューデント間のKLダイバージェンスを用いた蒸留損失。

$$L_{\text{distill}} = T^2 \cdot L_{\text{KL}}(p_T, p_S)$$

  • $L_{\text{KL}}(p_T, p_S)$：ティーチャー分布 $p_T$​ とスチューデント分布 $p_S$ 間のKLダイバージェンス。
    • モデル全体の損失は、蒸留損失とクロスエントロピー損失の加重和として定義されます。

$$L = \alpha L_{\text{CE}}(y, p_T) + \beta L_{\text{distill}}$$

  • $L_{\text{CE}}(y, p_T)$：正解ラベル $y$ とティーチャー分布 $p_T$ 間のクロスエントロピー損失。
  • $α,β$：損失間の重みを調整するハイパーパラメータ。

Self-Distillation のメリットとデメリット

メリット説明
自己改善外部のティーチャーモデルを必要とせず、自己学習によりモデル性能を向上させます。
汎化性能の向上中間層が出力層から情報を受け取り、モデル全体が一貫した表現を学習します。
リソース効率単一モデル内で完結するため、計算リソースの追加負担が少なく、効率的です。
デメリット説明
ハイパーパラメータ調整損失関数の重み（α, β）や温度パラメータ T の適切な設定が必要であり、調整に手間がかかる可能性があります。
適用対象の制限中間層が明確に定義されていないモデル（例：浅いネットワーク）では、自己蒸留の効果が限定的となる場合があります。

適用例：

適用例説明
画像認識ResNetなどの中間層を持つ深層学習モデルで有効。
自然言語処理Transformerアーキテクチャの中間層を活用。
軽量モデルの性能向上モデルサイズは変えずに内部知識を強化する際に活用。

Self-Distillationの蒸留損失関数の定義（PyTorch）：

import torch
import torch.nn.functional as F

def self_distillation_loss(output_logits, intermediate_features, labels, alpha=0.5, beta=0.5, temperature=2.0):
    """
    Self-Distillation 損失
    :param output_logits: 出力層のロジット (B, C)
    :param intermediate_features: 中間層の特徴量 (B, C)
    :param labels: 正解ラベル
    :param alpha: クロスエントロピー損失の重み
    :param beta: 蒸留損失の重み
    :param temperature: 温度スケール
    :return: 総合損失
    """
    # ティーチャーのソフトターゲット分布
    teacher_probs = F.softmax(output_logits / temperature, dim=1)

    # スチューデントのソフトターゲット分布
    student_probs = F.softmax(intermediate_features / temperature, dim=1)

    # 蒸留損失（KLダイバージェンス）
    distill_loss = F.kl_div(
        F.log_softmax(intermediate_features / temperature, dim=1),
        teacher_probs,
        reduction='batchmean'
    ) * (temperature ** 2)

    # クロスエントロピー損失
    ce_loss = F.cross_entropy(output_logits, labels)

    # 総合損失
    return alpha * ce_loss + beta * distill_loss

このコードでは、自己蒸留（Self-Distillation）を使用してモデルをトレーニングし、その精度を評価しています。自己蒸留損失関数は、モデルの出力層のロジットと中間層の特徴量を使用して、クロスエントロピー損失とKLダイバージェンス損失を組み合わせて総合損失を計算します。

論文：

Learning From Yourself: A Self-Distillation Method for Fake Speech Detection
In this paper, we propose a novel self-distillation method for fake speech detection (FSD), which can significantly impr...
arxiv.org
  • 自己蒸留フレームワークの新提案
    • 深いネットワークを「教師」、浅いネットワークを「生徒」として知識を伝える仕組みを導入。この方法で浅いネットワークが細かい特徴を捉える力を高め、偽音声検出の性能を大幅に向上させました。
  • トレーニング時のみ活用する軽量設計
    • トレーニング中に浅いネットワークに分類器を追加し、深いネットワークから知識を効率的に伝達。推論時には分類器を削除するため、計算負荷が増えない仕組みを採用しています。
  • ASVspoof 2019データセットでの成果
    • Logical Access (LA) と Physical Access (PA) データセットでの実験により、ベースラインモデルと比べて最大45%のEER削減を達成。さらに、この手法は複数のモデル構造で高い汎用性を示しました。

TinyTL (Tiny Transfer Learning)

TinyTLは、エッジデバイスやリソース制約のある環境向けに設計された効率的な転移学習手法です。この手法では、モデル全体を再学習するのではなく、特徴抽出器を固定し、一部のパラメータ（主にバイアス）だけを学習可能にします。これにより、メモリ使用量を削減しつつ、性能を維持します。さらに、知識蒸留の概念を組み込むことで、モデルの汎化性能を向上させることが可能です。

  • Feature Extractor の固定
    • ティーチャーモデルの大部分（バックボーン）は固定し、特徴量を抽出。
    • モデル全体のメモリ使用量を削減。
  • Bias Tuning
    • 主にバイアスパラメータを更新することで、効率的な微調整を実現。
  • ライトウェイト蒸留
    • 蒸留損失を用いてティーチャーモデルの知識を効率的に転移。

数式：

  • 転移学習における全体損失
    • 通常の転移学習では、全てのパラメータを更新する損失関数が使用されます。

$$L_{\text{total}} = \alpha L_{\text{CE}}(y, p) + \beta L_{\text{distill}}(p_T, p_S)$$

  • $L_{\text{CE}}(y, p)$：クロスエントロピー損失（正解ラベルとの誤差）。
  • $L_{\text{distill}}(p_T, p_S)$：ティーチャーとスチューデント間の蒸留損失（KLダイバージェンス）。
  • $α,β$：損失の重み。
  • TinyTL の Bias Tuning
    • TinyTL では、重み $W$ を固定し、主にバイアス $b$ を更新します。各層の出力は次のように定義されます。

$$f(x; W, b) = Wx + b$$

  • $W$：固定された重み。
  • $b$：学習可能なバイアス。

この制約により、更新するパラメータが大幅に減少し、学習効率が向上します。

  • メモリ効率の計算
    • 通常の転移学習と比較して、メモリ使用量は以下のように削減されます。

$$\text{Memory}_{\text{TinyTL}} = \text{Memory}_{\text{Feature Extractor}} + \text{Memory}_{\text{Bias Tuning}}$$

TinyTL のメリットとデメリット

メリット説明
メモリ効率の向上特徴抽出器を固定し、更新するパラメータを削減することで、メモリ使用量を削減します。
軽量デバイス向けエッジデバイスやリソース制約のある環境での学習に適しています。
パフォーマンスの維持モデル性能を大きく損なうことなく、効率的な学習を実現します。
デメリット説明
モデル構造の制約特徴抽出器が分離可能なモデル（例：ResNet）に限定される。
一部のタスクでの性能低下特に新しいデータ分布に対する柔軟性が必要な場合には限界がある。

適用例：

適用例説明
画像認識モバイルデバイス向けの画像分類（例：MobileNet）において、モデルの軽量化と性能維持を実現。
音声認識エッジデバイスでの音声コマンド認識に適用し、リアルタイム処理と省メモリ化を両立。
自然言語処理トークン分類やスロットフィリングタスクにおいて、モデルの効率的な微調整を可能にする。

TinyTLの蒸留損失関数の定義（PyTorch）：

TinyTL の Bias Tuning と蒸留を組み合わせた実装例です。

  • 特徴抽出器の固定
import torch
import torch.nn as nn

# モデルの定義
class TinyTLModel(nn.Module):
    def __init__(self, backbone, num_classes):
        super(TinyTLModel, self).__init__()
        self.feature_extractor = backbone  # 特徴抽出器
        self.feature_extractor.requires_grad_(False)  # パラメータを固定
        self.classifier = nn.Linear(backbone.output_dim, num_classes)  # バイアス更新のみ

    def forward(self, x):
        features = self.feature_extractor(x)
        output = self.classifier(features)
        return output
  • 損失関数の実装
import torch.nn.functional as F

def tinytl_loss(student_logits, teacher_logits, labels, alpha=0.5, beta=0.5, temperature=2.0):
    """
    TinyTL 損失関数
    :param student_logits: スチューデントモデルのロジット (B, C)
    :param teacher_logits: ティーチャーモデルのロジット (B, C)
    :param labels: 正解ラベル
    :param alpha: クロスエントロピー損失の重み
    :param beta: 蒸留損失の重み
    :param temperature: 温度スケール
    :return: 総合損失
    """
    # クロスエントロピー損失
    ce_loss = F.cross_entropy(student_logits, labels)

    # 蒸留損失（KLダイバージェンス）
    distill_loss = F.kl_div(
        F.log_softmax(student_logits / temperature, dim=1),
        F.softmax(teacher_logits / temperature, dim=1),
        reduction='batchmean'
    ) * (temperature ** 2)

    # 総合損失
    return alpha * ce_loss + beta * distill_loss

論文：

TinyTL: Reduce Activations, Not Trainable Parameters for Efficient On-Device Learning
On-device learning enables edge devices to continually adapt the AI models to new data, which requires a small memory fo...
arxiv.org
  • メモリ効率の革新
    • TinyTLは、重みを固定しバイアスだけを調整する仕組みにより、中間のデータを保存する必要をなくしました。その結果、従来の方法と比べてメモリ使用量を最大12.9倍も削減しています。
  • 精度と効率の両立
    • TinyTLは、重み全体ではなくバイアスとLite Residual Moduleだけを調整する方法を採用しました。これにより、わずか約3.8%のメモリ追加で、精度を最大34.1%向上させることに成功しました。
  • オンデバイス学習の実現
    • TinyTLは、エッジデバイスの限られたメモリとエネルギーに対応し、DRAMへの依存を減らしました。その結果、効率的で拡張性のあるオンデバイス学習を実現しました。

Data-Free Knowledge Distillation（DFKD）

Data-Free Knowledge Distillation（DFKD）は、元のトレーニングデータを使用せずに、ティーチャーモデルの知識をスチューデントモデルに転移する手法です。これは、データセキュリティやプライバシーの観点から元データの使用が制限される場合に有効です。DFKDでは、生成モデルを用いて擬似データを生成し、ティーチャーモデルの出力に適合するように学習させます。この方法により、元データなしで効果的な知識蒸留が可能となります。

数式：DFKD の損失関数は、以下の2つの主要なコンポーネント（データ生成の最適化・蒸留損失）で構成されます。

  • データ生成の最適化
    • 生成モデル $G(z)$ はランダムノイズ $z$ を入力とし、擬似データ $\hat{x}$ を生成します。この擬似データがティーチャーモデルの特徴空間に適合するように最適化されます。

$$\hat{x} = G(z), \quad z \sim \mathcal{N}(0, I)$$

生成されたデータに対するティーチャーモデルの出力を $p_T(\hat{x})$、スチューデントモデルの出力を $p_S(\hat{x})$ とすると、生成損失は以下で定義されます。

$$L_{\text{gen}} = -H(p_T(\hat{x})) + \lambda \|\nabla_x p_T(\hat{x})\|^2$$

  • $H(p_T(\hat{x}))$：ティーチャーモデルのエントロピー（擬似データの不確実性を低下）。
  • $\|\nabla_x p_T(\hat{x})\|^2$：ティーチャーモデルの勾配正則化項（スムーズな生成を保証）。
  • $λ$：正則化項の重み。
  • 蒸留損失
    • ティーチャーモデルとスチューデントモデルの出力分布を一致させるため、KLダイバージェンスが用いられます。

$$L_{\text{distill}} = KL(p_T(\hat{x}) \| p_S(\hat{x}))$$

  • 総合損失
    • 生成モデルとスチューデントモデルを共同で最適化するための総合損失は次の通りです。

$$L_{\text{total}} = L_{\text{distill}} + \alpha L_{\text{gen}}$$

  • $α$：生成損失と蒸留損失のバランスを取るハイパーパラメータ。

DFKD のメリットとデメリット

メリット説明
データセキュリティ元データを使用しないため、データセキュリティやプライバシーが重要な場合に有効です。
軽量化モデルと生成データを利用するだけで学習が可能です。
適用範囲の広ささまざまなドメイン（画像、テキスト、音声）に適用可能です。
デメリット説明
生成モデルの訓練コスト擬似データを生成するための計算コストが追加される。
生成データの品質依存生成されたデータの品質が低いと、スチューデントモデルの性能が低下。

適用例：

適用例説明
セキュリティが求められる環境医療データや金融データなど、機密性の高いデータを扱う場合。
エッジデバイスでのモデル圧縮データ転送が困難な環境での知識蒸留。
生成モデルとの統合GANやVAEを活用した知識転移。

DFKDの蒸留損失関数の定義（PyTorch）：

  • 生成モデルの定義
import torch
import torch.nn as nn
import torch.nn.functional as F

class Generator(nn.Module):
    def __init__(self, latent_dim, img_size):
        super(Generator, self).__init__()
        self.model = nn.Sequential(
            nn.Linear(latent_dim, 128),
            nn.ReLU(),
            nn.Linear(128, img_size),
            nn.Tanh()
        )

    def forward(self, z):
        return self.model(z)
  • 損失関数の実装
def data_free_loss(teacher_model, student_model, generator, latent_dim, alpha=1.0, lambda_reg=0.01):
    """
    Data-Free Knowledge Distillation 損失関数
    :param teacher_model: ティーチャーモデル
    :param student_model: スチューデントモデル
    :param generator: 生成モデル
    :param latent_dim: ノイズ次元
    :param alpha: 蒸留損失と生成損失のバランス
    :param lambda_reg: 勾配正則化の重み
    :return: 総合損失
    """
    # ノイズから擬似データを生成
    z = torch.randn(batch_size, latent_dim).to(device)
    generated_data = generator(z)

    # ティーチャーとスチューデントの出力を取得
    teacher_logits = teacher_model(generated_data)
    student_logits = student_model(generated_data)

    # 蒸留損失（KLダイバージェンス）
    distill_loss = F.kl_div(
        F.log_softmax(student_logits, dim=1),
        F.softmax(teacher_logits, dim=1),
        reduction='batchmean'
    )

    # 生成損失
    entropy_loss = -torch.mean(torch.sum(F.softmax(teacher_logits, dim=1) * F.log_softmax(teacher_logits, dim=1), dim=1))
    grad_reg_loss = torch.mean(torch.norm(torch.autograd.grad(teacher_logits.sum(), generated_data, create_graph=True)[0], dim=1) ** 2)
    gen_loss = -entropy_loss + lambda_reg * grad_reg_loss

    # 総合損失
    total_loss = distill_loss + alpha * gen_loss
    return total_loss

生成モデルを使用して擬似データを生成し、そのデータを用いて教師モデルから生徒モデルへ知識を蒸留します。損失関数は、蒸留損失（KLダイバージェンス）と生成損失（エントロピー損失と勾配正則化損失）を組み合わせて計算されます。これにより、元のデータセットを使用せずに知識蒸留を行うことができます。

論文：

Zero-shot Knowledge Transfer via Adversarial Belief Matching
Performing knowledge transfer from a large teacher network to a smaller student is a popular task in modern deep learnin...
arxiv.org

この論文におけるDFKDの成果

  • データ非依存のゼロショット知識蒸留
    • トレーニングデータなしで知識を移すゼロショット蒸留手法を開発。生成器が生徒の弱点を見つけ出し、改善に役立つ画像を自動生成します。これにより、データやメタ情報に依存せず、プライバシーや知財制約をクリアできるのが特長です。
  • SVHNとCIFAR-10での性能向上
    • SVHNでは教師とほぼ同等の精度を達成し、CIFAR-10ではデータなしで従来の少数ショット蒸留手法を超える成果を実現しました。特に、1クラスあたり100枚以下の少ない画像条件でも、最先端の精度を示しています。
  • 信念一致の新指標提案
    • 教師と生徒の決定境界付近での「信念の一致度」を測る新しい指標を提案しました。この指標を用いることで、従来のデータを使用する手法よりも高い一致度を数値的に証明することに成功しました。

信念の一致度とは？

「信念の一致度」とは、教師モデルと生徒モデルが同じデータに対してどれだけ似た予測をするかを示す指標です。特に、クラス分けが難しい決定境界付近での一致を評価することで、知識蒸留の効果を測ることができます。本論文では、この一致度を評価するために、教師と生徒が出力するクラス確率の違いを数値的に測定（例: KLダイバージェンス）します。この指標は、ゼロショット環境における知識移転がどれほど成功したかを確認する重要な手法です。研究結果として、従来のデータを使った手法よりも、提案するゼロショット蒸留手法の方が高い一致度を示し、教師から生徒への知識移転がより効果的であることが明らかになりました。

  • 「信念の一致度」を数値的に測定する方法
    • KLダイバージェンス
    • コサイン類似度
    • L2ノルム距離
    • ジニ係数
    • ジューカーニュクレール距離
    • クロスエントロピー
    • Earth Mover’s Distance(EMD)
    • トータルバリエーション距離
指標名特徴適用シナリオ
KLダイバージェンス非対称性を持ち、ある分布が別の分布からどれだけ情報を失うかを測定します。分布の形状やスケールが重要な場合。
JSダイバージェンスKLダイバージェンスの対称化バージョンで、2つの分布の平均からの乖離を測定します。分布の形状やスケールが重要な場合。
Earth Mover’s Distance (Wasserstein 距離)分布間の質量を移動する最小コストを測定し、分布の全体的な形状の違いを捉えます。分布の形状やスケールが重要な場合。
コサイン類似度2つのベクトル間の角度を測定し、類似度を評価します。計算が効率的です。計算効率を優先する場合。
L2ノルム距離 (ユークリッド距離)2つのベクトル間の直線距離を測定します。計算が効率的です。計算効率を優先する場合。
Total Variation Distance2つの分布間の最大差異を測定し、局所的な違いに敏感です。局所的な違いに敏感な指標が必要な場合。
KL ダイバージェンス2つの分布間の差異を測定しますが、非対称性があります。局所的な違いに敏感な指標が必要な場合。

これらの方法を組み合わせることで、信念一致度を多面的に評価できます。

枝刈り（Pruning）

プルーニング（枝刈り）は、ニューラルネットワークの不要なパラメータや接続を削減し、モデルのサイズや計算量を削減する手法です。これにより、メモリ使用量の削減や推論速度の向上が可能となり、リソース制約のある環境（例：エッジデバイス）での適用が容易になります。さらに、プルーニングは量子化や知識蒸留などの他のモデル圧縮手法と組み合わせることで、性能を維持しつつ、より効果的なモデル軽量化が実現できます。

Puringのイメージ図：

図3：刈り込み前後のシナプスとニューロンプルーニング。
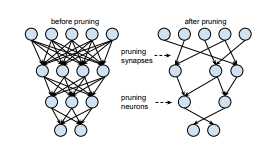
論文：『Learning both Weights and Connections for Efficient Neural Networks』（https://arxiv.org/pdf/1506.02626）から引用

Pruning の主な目的

  • 軽量化：モデルサイズを削減。
  • 推論速度向上：計算量を減少。
  • リソース効率化：デバイスに応じた適応。

Pruning の種類

  • 要素レベルの Pruning
    • 個々のパラメータ（重み）を基準に削除。
    • 条件：小さい値（例：ゼロに近い重み）。
  • 構造化 Pruning
    • ネットワーク構造全体を削除対象に。
      • 例：特定のチャネル、フィルタ、層を削除。
  • 動的 Pruning
    • 推論中に入力データに基づいて構造を変更。
    • 例：不要なノードや層をスキップ。

これらの手法を組み合わせることで、モデルのサイズを削減し、計算効率を向上させることができます。

数式：

  • 重みの選択基準
    • 各重み $w$ に対して、その絶対値 $|w|$ が小さいものを削除する場合

$$\text{Mask}(w_i) =
\begin{cases}
1, & \text{if } |w_i| > \tau \\
0, & \text{if } |w_i| \leq \tau
\end{cases}$$

  • $τ$：削除の閾値。
  • Mask は削除されるパラメータを示す。
  • 構造化 Pruning
    • 例えば、フィルタ単位での削除の場合、フィルタの $L_1$​ ノルムを基準に削除します。

$$\|W_i\|_1 = \sum_{j,k} |W_{i,j,k}|$$

  • $W_i$​：フィルタ $i$。
  • $\|W_i|_1$：フィルタの重要度を評価。

重要度が小さいフィルタを削除します。

  • Pruning による損失
    • Pruning を適用した後の再トレーニングでは、通常の損失関数に正則化項を追加して学習します。

$$L = L_\text{task} + \lambda \|W\|_0$$

  • $L_\text{task}$：通常のタスク損失（例：クロスエントロピー）。
  • $\|W|_0$​：非ゼロ要素の数を表す $L_0$ ノルム。
  • $λ$：正則化の重み。

Pruning のメリットとデメリット

メリット説明
軽量化モデルサイズが削減されるため、デバイス適応が容易。
推論速度の向上計算量が削減され、リアルタイム推論が可能。
メモリ効率の向上不要なパラメータを削除することで、メモリ使用量を削減。
デメリット説明
性能劣化Pruning によって性能が低下する場合がある。
再トレーニングの必要性削減後の性能維持には追加のトレーニングが必要。
複雑な制御構造化 Pruning の場合、ハードウェアとの整合性を考慮する必要がある。

適用例：

適用例説明
エッジデバイスモバイルデバイスや IoT デバイス向けの軽量化。
リアルタイム推論推論時間を短縮するための効率化。
分散学習軽量化したモデルを分散環境で適用。

要素レベルの Pruningの実装例

個々の重みを削除する手法で、L1ノルムやL2ノルムに基づいて、最も小さい重みを削除します。

import torch
import torch.nn as nn
import torch.nn.utils.prune as prune

# シンプルなモデル定義
class SimpleModel(nn.Module):
    def __init__(self):
        super(SimpleModel, self).__init__()
        self.fc1 = nn.Linear(100, 50)
        self.fc2 = nn.Linear(50, 10)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        return self.fc2(x)

model = SimpleModel()

# fc1 層に対して要素レベルの Pruning を適用
prune.l1_unstructured(model.fc1, name='weight', amount=0.5)

# 削除後の重み
print(model.fc1.weight)
  • prune.l1_unstructured(model.fc1, name='weight', amount=0.5) は、fc1 層の重みの50%を削除します。
  • 要素レベルの Pruning は、モデルのスパース性を高めますが、計算効率の向上には限界があります。

構造化 Pruningの実装例

特定の構造（例: チャネル、フィルタ、層）全体を削除する手法です。これにより、モデルの計算効率が向上します。

# チャネル単位での削除
prune.ln_structured(model.fc1, name="weight", amount=0.3, n=2, dim=0)

# チャネル削除後の重み
print(model.fc1.weight)
  • prune.ln_structured(model.fc1, name="weight", amount=0.3, n=2, dim=0) は、fc1 層の重みの30%をチャネル単位で削除します。

動的 Pruningの実装例

トレーニング中に動的に重みを削除する手法です。トレーニングの進行に応じて、重みの削除と再トレーニングを繰り返します。

# Pruning 後の再トレーニング
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
criterion = nn.CrossEntropyLoss()

for epoch in range(10):
    optimizer.zero_grad()
    output = model(torch.randn(64, 100))  # ダミーデータ
    loss = criterion(output, torch.randint(0, 10, (64,)))
    loss.backward()
    optimizer.step()

    # 動的 Pruning を適用
    prune.l1_unstructured(model.fc1, name='weight', amount=0.1)

    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")
  • 再トレーニングのループで、Pruning 後のモデルをトレーニングします。
  • 動的 Pruning はモデルの性能を維持しながらスパース性を高めることができます。

これらの手法を組み合わせることで、モデルのサイズを削減し、計算効率を向上させることができます。以下は上で紹介した手法を組み合わせた実装例です。

このコードでは、要素レベルの Pruning、構造化 Pruning、および動的 Pruning を組み合わせて、CIFAR-10 データセットを使用して ResNet18 モデルをトレーニングし、モデルの精度を向上させる手法を実装しています。

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torch.nn.utils.prune as prune
from torchvision import datasets, transforms, models
from torch.utils.data import DataLoader

# データの準備（CIFAR-10データセットを使用）
transform = transforms.Compose([
    transforms.Resize((224, 224)),  # ResNet18の入力サイズに合わせる
    transforms.ToTensor(),
    transforms.Normalize((0.485, 0.456, 0.406), (0.229, 0.224, 0.225))
])
train_dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_dataset = datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=False)

# モデルのインスタンス化
model = models.resnet18(pretrained=True)
model.fc = nn.Linear(model.fc.in_features, 10)  # CIFAR-10に合わせて出力層を変更
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
model.to(device)

# 損失関数とオプティマイザ
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# モデルのトレーニングと Pruning
num_epochs = 10
for epoch in range(num_epochs):
    model.train()
    for data, target in train_loader:
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = criterion(output, target)
        loss.backward()
        optimizer.step()

    # 要素レベルの Pruning を適用
    prune.l1_unstructured(model.layer1[0].conv1, name='weight', amount=0.1)
    prune.l1_unstructured(model.layer1[0].conv2, name='weight', amount=0.1)

    # 構造化 Pruning を適用
    prune.ln_structured(model.layer1[0].conv1, name='weight', amount=0.1, n=2, dim=0)
    prune.ln_structured(model.layer1[0].conv2, name='weight', amount=0.1, n=2, dim=0)

    print(f"Epoch {epoch+1}, Loss: {loss.item():.4f}")

# Pruning 後の再トレーニング
for epoch in range(5):
    model.train()
    for data, target in train_loader:
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = criterion(output, target)
        loss.backward()
        optimizer.step()

    print(f"Re-training Epoch {epoch+1}, Loss: {loss.item():.4f}")

# モデルの評価
model.eval()
correct = 0
total = 0
with torch.no_grad():
    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        output = model(data)
        _, predicted = torch.max(output.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()

print(f"Accuracy of the pruned model on the test images: {100 * correct / total:.2f}%")

Pruning によってモデルのサイズを削減し、再トレーニングによって性能を回復させることで、効率的なモデルを構築します。

論文1：

Learning both Weights and Connections for Efficient Neural Networks
Neural networks are both computationally intensive and memory intensive, making them difficult to deploy on embedded sys...
arxiv.org
  • わかりやすく効率的なプルーニング手法
    • 重要な接続を見極めて残し、不要な接続を削除した後に再学習する3つのステップで、モデルの無駄を削減。この手法により、モデルサイズを大幅に小さくしつつ、精度をそのまま保つことが可能です。
  • 実証された圧縮効果
    • 提案手法により、ImageNetデータセットでAlexNetは9倍、VGG-16は13倍の圧縮を実現。精度を維持したまま大幅に軽量化し、モバイルデバイスでも効率的に動作可能となりました。
  • 脳をヒントにした柔軟なネットワーク設計
    • 提案手法の特徴は、哺乳類の脳で行われる「シナプス剪定」に着想を得ている点です。生物学的には、脳の神経回路は幼少期に多数のシナプスを形成し、その後、使用頻度の低い接続を削除することで効率的な回路を構築します。同様に、この手法では、ニューラルネットワーク内の重要な接続を特定し、不要な接続を削除（プルーニング）した上で、残った接続を再学習します。これにより、ネットワーク構造が動的に最適化され、精度を維持しながらモデルサイズと計算コストを削減可能です。
      特に、削除後の再学習（リトレーニング）によって、削除された接続を補うように残された接続が調整される点が重要です。このプロセスにより、計算効率の向上とエネルギー消費の削減が実現され、モバイルデバイスのようなリソースが限られた環境でも高度なニューラルネットワークの利用が可能になります。生物の学習メカニズムを活用したこのアプローチは、AI技術のさらなる進展に向けた応用可能性を示しています。

論文２：

The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks
Neural network pruning techniques can reduce the parameter counts of trained networks by over 90%, decreasing storage re...
arxiv.org
  • 宝くじ仮説の提唱
    • 「宝くじ仮説」とは、適切な初期化とプルーニングによって選ばれた疎なサブネットワークが、元の密なネットワークと同じ性能を発揮できるという考え方です。この発見は、効率的な学習方法の手がかりを示しています。
  • プルーニングの有効性
    • プルーニングは、小さな重みを削除することで、モデルサイズを90%以上削減しながらも精度を維持できる手法です。この結果は、計算効率の向上とストレージ節約を同時に実現する可能性を示しています。
  • 実験による仮説の確認
    • CIFAR-10やMNISTといったデータセットや、ResNetやVGGなどのモデルを使った実験で仮説を検証しました。その結果、小規模な問題では、疎なモデルが元のモデルよりも収束が速く、精度が高くなる場合があることが確認されました。

宝くじ仮説とは？

宝くじ仮説（Lottery Ticket Hypothesis）は、ランダムに初期化された密なニューラルネットワークの中に、特定の疎なサブネットワークが隠れており、そのサブネットワークだけで元のネットワークと同等の性能を発揮できるという考え方です。このサブネットワークは「宝くじの当たり券」にたとえられ、適切な初期化がその性能の鍵を握ります。また、プルーニングによって不要な重みを削除することで、モデルのサイズを大幅に削減しながらも性能を維持できることが確認されています。CIFAR-10やMNISTなどのデータセット、ResNetやVGGなどのモデルを使った実験では、特に小規模なタスクにおいて、疎なモデルの方が収束が速く高精度であることが示されました。この仮説は、効率的な学習方法やモデルの圧縮技術に新たな方向性を提供しています。

Puring（枝刈り）に類似したモデル

Puringは以下の方法などと組み合わせることにおいてモデルの精度を上げることが可能なアルゴリズムです。この方法を工夫し、宝くじ仮説などにチャレンジしてみましょう。

技術名概要適用例
量子化（Quantization）パラメータの精度を削減（例：32ビット浮動小数点 → 8ビット整数）し、メモリ使用量と計算量を抑制。モバイルやエッジデバイス向けの軽量な推論モデル。
知識蒸留（Knowledge Distillation）大規模なティーチャーモデルから小規模なスチューデントモデルへ知識を転移し、性能を維持。リソース制約のある環境での軽量モデル作成。
モデル圧縮（Model Compression）Pruning と Quantization を組み合わせ、他の補完技術（蒸留や重み共有）でさらに効果向上。データセンターからエッジデバイスへのモデル移行。
ネットワークアーキテクチャ検索（NAS）効率的なモデル構造を自動探索し、最初から軽量なアーキテクチャを設計。MobileNet や EfficientNet のようなモバイル向けモデル設計。
スパース化（Sparsification）重み行列を疎にする（多くをゼロにする）ことで計算コストを削減し、行列全体の構造を最適化。スパース行列ライブラリを活用した推論効率化。
重み共有（Weight Sharing）複数の層や接続で同じパラメータを共有し、さらなる軽量化を実現。リソースが限られた環境での推論モデル作成。
蒸留 + Pruning の統合蒸留による知識転移と Pruning を組み合わせ、不要な部分を削減しつつ性能を維持。軽量化と高性能を両立したモデル作成。
動的推論（Dynamic Inference）入力データに応じてネットワークの一部のみを使用（例：SkipNet で層をスキップ）。低遅延のリアルタイム推論。
削減済みアーキテクチャ（Pre-Pruned Architectures）Pruning 後のモデルを再トレーニングして性能劣化を回復。Pruning 後のモデル微調整。
構造化 Pruning（Structured Pruning）特定の層単位やチャネル単位で削減し、ハードウェア効率を向上。CNN のチャネル削減（例：モバイルデバイス向け）。

量子化

量子化（Quantization）は、ニューラルネットワークのパラメータやアクティベーションを低精度の数値形式に変換することで、モデルの軽量化と推論速度の向上を図る手法です。これにより、リソース制約のあるデバイスでの効率的なモデル推論が可能となります。量子化には、主に学習後にモデルを量子化する Post-Training Quantization（PTQ）と、学習中に量子化を考慮する Quantization-Aware Training（QAT）の2種類があります。さらに、Pruning（枝刈り）や知識蒸留などの他のモデル軽量化手法と組み合わせることで、モデルの性能とリソース効率のバランスを最適化できます。

量子化のイメージ：

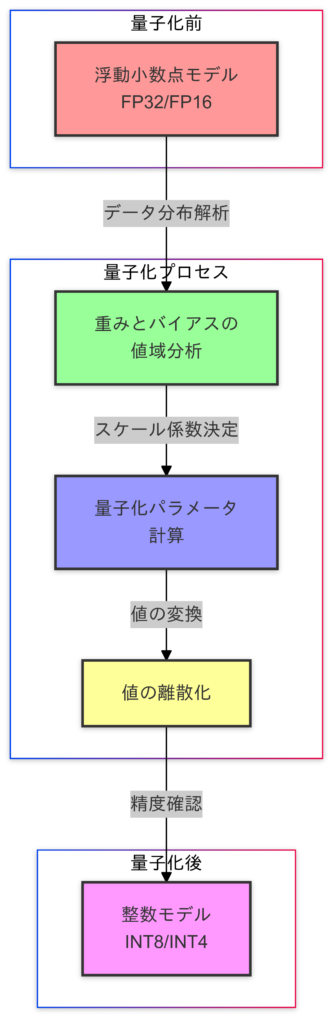
量子化の種類

  • 重みの量子化
    • モデルの重みパラメータを低精度フォーマットに変換。
    • メモリ使用量を削減。
  • アクティベーションの量子化
    • アクティベーション（中間層の出力）を量子化。
    • 推論時の計算負荷を低減。
  • 訓練済みモデルの量子化（Post-Training Quantization, PTQ）
    • 訓練後のモデルを量子化。
    • 再トレーニングが不要。
  • 量子化対応訓練（Quantization-Aware Training, QAT）
    • 訓練中に量子化をシミュレート。
    • 精度の低下を最小限に抑える。

QATに至っては実装中にエラーが出てしまいましたので実装例は記述していません。

数式：

  • 量子化操作
    • 量子化は、連続値を固定ビット幅で表現可能な離散値にマッピングする操作です。

$$q(x) = \text{round} \left( \frac{x – x_{\text{min}}}{s} \right) \cdot s + x_{\text{min}}$$

  • $q(x)$：量子化された値。
  • $x$：元の値。
  • $x_{min}​,x_{max}$​：値の最小・最大範囲。
  • $s = \frac{x_{\text{max}} – x_{\text{min}}}{2^b – 1}$：スケールファクター（量子化ステップサイズ）。
  • $b$：ビット数（例：8ビットなら $b=8$）。
  • 量子化の誤差
    • 量子化に伴う誤差は次のように定義されます。

$$e(x) = x – q(x)$$

量子化のメリットとデメリット

メリット説明
モデル軽量化低ビット表現によりメモリ消費を削減。
推論速度向上低ビット演算は高速化に寄与。
汎用性既存の訓練済みモデルにも適用可能（PTQ）。
デメリット説明
精度低下特に PTQ では量子化誤差による性能劣化が発生。
デバイス依存特定のハードウェアでの最適化が必要。
計算オーバーヘッドQAT は訓練コストが増加。

適用例：

適用例説明
エッジデバイスモバイル端末や IoT デバイスでの軽量モデル適用。
リアルタイム推論高速性が求められるアプリケーション（例：自動運転、リアルタイム画像認識）。
モデル圧縮大規模言語モデルや画像モデルの圧縮。

PTQの実装例

PTQは、トレーニング後にモデルを量子化する手法であり、追加のトレーニングを必要とせず、簡単に適用できるという利点があります。ただし、精度の低下が発生する可能性があるため、適切なキャリブレーションと量子化手法を使用することが重要です。PTQは、特定のハードウェアバックエンドに最適化された量子化を適用することで、リソース制約のあるデバイスでの効率的な推論を実現します。

import torch
import torch.nn as nn
import torch.quantization

# モデル定義
class SimpleModel(nn.Module):
    def __init__(self):
        super(SimpleModel, self).__init__()
        self.fc = nn.Linear(100, 10)

    def forward(self, x):
        return self.fc(x)

# 訓練済みモデルのロード
model = SimpleModel()
model.eval()  # 推論モード

# 量子化の準備
model.qconfig = torch.quantization.get_default_qconfig('fbgemm')
torch.quantization.prepare(model, inplace=False)

# 擬似データで量子化パラメータをキャリブレーション
for _ in range(10):
    dummy_input = torch.randn(1, 100)
    model(dummy_input)

# 量子化
quantized_model = torch.quantization.convert(model, inplace=False)
print(quantized_model)
  • model.qconfig に torch.quantization.get_default_qconfig('fbgemm') を設定します。fbgemm は、x86プラットフォーム向けの量子化バックエンドです。
  • torch.quantization.prepare(model, inplace=False) を呼び出して、モデルを量子化の準備状態にします。これにより、量子化のためのスケールとゼロポイントが計算されます。

論文１：

Quantized Neural Networks: Training Neural Networks with Low Precision Weights and Activations
We introduce a method to train Quantized Neural Networks (QNNs) --- neural networks with extremely low precision (e.g., ...
arxiv.org
  • 低精度でのトレーニング
    • 量子化ニューラルネットワーク（QNN）は、重みと活性化を1ビット精度に減らすことで、メモリ使用量と計算量を大幅に削減します。それでも高い精度を保ち、効率的に学習を進めることができます。
  • 高速化とエネルギー効率
    • ビット単位での演算により計算速度が向上し、GPUでの処理が高速化します。また、エネルギー消費も従来の方法に比べて大幅に削減され、1桁以上の節約が実現します。
  • 高精度な分類結果
    • MNIST、CIFAR-10、SVHNなどのデータセットで高精度な分類を達成しました。また、ImageNetではバイナリ化されたモデルが優れた分類精度を示し、効率的なトレーニングが可能です。

論文2：

A White Paper on Neural Network Quantization
While neural networks have advanced the frontiers in many applications, they often come at a high computational cost. Re...
arxiv.org
  • 量子化による効率化
    • 量子化による効率化では、ニューラルネットワークの計算量とメモリ使用量を減らすために、8ビットの量子化が活用されます。これにより、計算時間やメモリの消費が大幅に削減され、精度をほとんど損なうことなく効率的に処理できる点が重要です。
  • ポストトレーニング量子化（PTQ）
    • ポストトレーニング量子化（PTQ）は、再学習なしで高精度を維持できる簡単な手法です。特に、32ビットから8ビットへの変換によって、性能を向上させることができます。
  • 量子化対応学習（QAT）の効果
    • 量子化対応学習（QAT）は、量子化による誤差を修正し、ポストトレーニング量子化よりも高い精度を実現します。しかし、トレーニングにかかる時間やデータのコストが増えるというデメリットがあります。
様々な量子化モデル

前述で紹介したPTQ、QATの他のモデルも存在します。モデルの精度を上げるために特徴や適用例を参考に活用してみましょう。

モデル名概要特徴適用例
Post-Training Quantization (PTQ)トレーニング後に重みやアクティベーションを低精度に変換。追加トレーニング不要で手軽に適用可能。モバイルやエッジデバイスでのモデル展開。
Quantization-Aware Training (QAT)トレーニング中に量子化の影響を考慮し、精度低下を最小限に抑える。量子化誤差に対応し、精度を高く保つ。精度を重視しつつ量子化を導入する場合。
Mixed-Precision Quantizationレイヤーや演算ごとに異なるビット幅を使用。精度とモデルサイズのバランスを最適化。モバイルデバイスや専用ハードウェアでの推論。
Adaptive Quantizationデータやモデルの動作に応じて動的に量子化レベルを変更。システム負荷に応じて適応可能。リアルタイムアプリケーションでの省電力動作。
Progressive Quantizationモデルを段階的に量子化して精度を確保。トレーニング済みモデルへの影響を段階的に評価可能。大規模モデルの圧縮。
最近の研究からのモデル
モデル名概要特徴
Binarized Neural Networks (BNNs)重みとアクティベーションをバイナリ（1ビット）に変換。推論速度が飛躍的に向上する一方で、精度低下の課題あり。
Ternary Neural Networks (TNNs)重みを3値（-1, 0, 1）のみに制限。BNNと比較して精度が向上。
QNNs with Learned Quantization Parameters量子化のスケールやオフセットを学習プロセスで最適化。固定パラメータよりも柔軟で高精度。
Differentiable Quantization量子化を微分可能な形式に拡張。微分可能な量子化により、より滑らかな最適化が可能。

Early Stopping（早期終了）

Early Stopping（早期終了）は、検証データの性能（損失や精度）に基づいて学習を途中で停止し、過学習を防止する正則化手法です。訓練データの損失が減少していても、検証データの損失が増加し始めるタイミングで学習を終了します。この手法はシンプルでさまざまな学習シナリオに適用可能であり、効率的なトレーニングを実現します。他の正則化手法（例: ドロップアウト、正則化項）と併用することで、さらなる性能向上が期待できます。

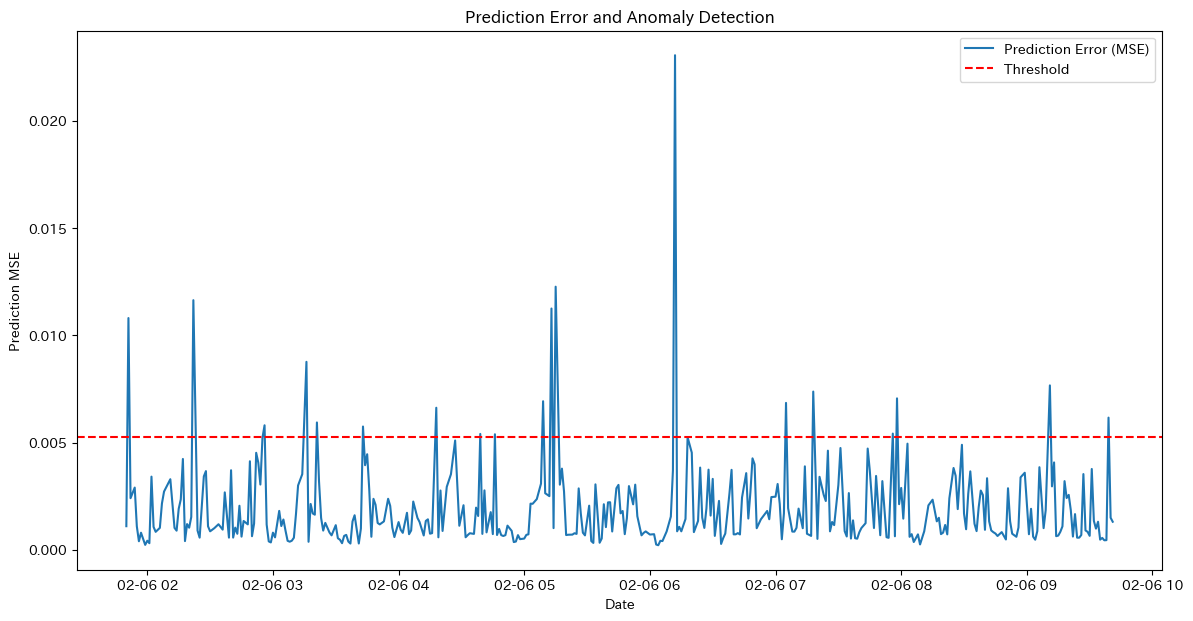
https://zero2one.jp/ai-word/early-stopping/より抜粋

目的：

  • 過学習防止
    • モデルが訓練データに過剰適合するのを防ぐ。
  • 効率的な学習
    • 無駄なエポックを減らし、計算リソースを節約。

数式：

  • モデル損失の追跡
    • 訓練データと検証データの損失を $L_{\text{train}}$​ および $L_{\text{val}}$とします。検証損失 $L_{\text{val}}$​ が、一定期間（例: patience）内で改善しない場合に学習を停止します。
  • 条件式
    • Early Stopping の条件は以下のように定義されます。

$$L_{\text{val}}^{(t)} > L_{\text{val}}^{(t – \Delta t)} \quad \text{for } \Delta t = 1, \dots, \text{patience}$$

  • $t$：現在のエポック。
  • $\Delta t$：検証損失が悪化している期間。
  • patience：停止するまで許容される悪化のエポック数。

Early Stoppingのメリットとデメリット

メリット説明
過学習防止検証データの性能を監視することで、モデルが訓練データに過適合するのを防ぎます。
効率的学習を早期に終了することで、計算リソースを節約。
柔軟性patience や delta など、停止条件を細かく調整可能。
デメリット説明
検証データ依存検証データが不適切な場合、モデル性能が損なわれる可能性があります。
パラメータ調整の必要性patience や delta の設定次第で結果が変わる。
実装の手間簡易的なトレーニングループには追加の実装が必要。

適用例：

適用例説明
データ量が少ないタスク過学習が起こりやすい状況で有効。
計算リソースが限られている場合早期終了によりトレーニングコストを削減。
長時間学習タスク不要なエポックを削減することで時間を節約。

Early Stoppingの実装例：

Early Stoppingは、検証データの損失を監視しながら、適切なタイミングで学習を停止する正則化手法です。過学習を防ぎ、効率的なトレーニングを実現するため、非常に有用です。また、ドロップアウトやL2正則化といった他の正則化手法と組み合わせることで、さらなる性能向上が期待できます。

以下のコードでは、ドロップアウトとL2正則化という異なる正則化手法を使用してモデルをトレーニングし、それぞれが検証損失に与える影響を比較しています。トレーニングではEarly Stoppingを導入し、学習を早期に終了することで最適な状態を確保します。これにより、どの正則化手法が最も効果的であるかを検証データの損失を基準に評価できます。

import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset

class EarlyStopping:
    def __init__(self, patience=5, delta=0, verbose=False, path='checkpoint.pt'):
        self.patience = patience
        self.delta = delta
        self.verbose = verbose
        self.path = path
        self.counter = 0
        self.best_loss = np.Inf
        self.early_stop = False

    def __call__(self, val_loss, model):
        if val_loss < self.best_loss - self.delta:
            self.best_loss = val_loss
            self.counter = 0
            self.save_checkpoint(model)
        else:
            self.counter += 1
            if self.counter >= self.patience:
                self.early_stop = True

    def save_checkpoint(self, model):
        if self.verbose:
            print(f"Validation loss decreased. Saving model...")
        torch.save(model.state_dict(), self.path)

# モデルの定義（ドロップアウト付き）
class ModelWithDropout(nn.Module):
    def __init__(self, dropout_rate=0.5):
        super(ModelWithDropout, self).__init__()
        self.linear = nn.Linear(10, 1)
        self.dropout = nn.Dropout(dropout_rate)

    def forward(self, x):
        x = self.dropout(x)
        return self.linear(x)

# ダミーデータの作成
X_train, y_train = torch.randn(100, 10), torch.randn(100, 1)
X_val, y_val = torch.randn(20, 10), torch.randn(20, 1)

train_dataset = TensorDataset(X_train, y_train)
val_dataset = TensorDataset(X_val, y_val)

train_loader = DataLoader(train_dataset, batch_size=32)
val_loader = DataLoader(val_dataset, batch_size=20)

# 1. ドロップアウトと L2 正則化なし
print("----- 1. ドロップアウトと L2 正則化なし -----")
model_no_reg = nn.Linear(10, 1)
criterion = nn.MSELoss()
optimizer_no_reg = optim.SGD(model_no_reg.parameters(), lr=0.01)
early_stopping_no_reg = EarlyStopping(patience=3, verbose=True)

for epoch in range(50):
    model_no_reg.train()
    for batch_X, batch_y in train_loader:
        optimizer_no_reg.zero_grad()
        y_pred = model_no_reg(batch_X)
        loss = criterion(y_pred, batch_y)
        loss.backward()
        optimizer_no_reg.step()

    model_no_reg.eval()
    with torch.no_grad():
        val_pred = model_no_reg(X_val)
        val_loss = criterion(val_pred, y_val).item()

    print(f"Epoch {epoch+1}, Validation Loss: {val_loss:.4f}")

    early_stopping_no_reg(val_loss, model_no_reg)
    if early_stopping_no_reg.early_stop:
        print("Early stopping triggered.")
        break

model_no_reg.load_state_dict(torch.load('checkpoint.pt'))

# 2. ドロップアウトあり、L2 正則化なし
print("\n----- 2. ドロップアウトあり、L2 正則化なし -----")
model_dropout = ModelWithDropout(dropout_rate=0.5)
optimizer_dropout = optim.SGD(model_dropout.parameters(), lr=0.01)
early_stopping_dropout = EarlyStopping(patience=3, verbose=True)

for epoch in range(50):
    model_dropout.train()
    for batch_X, batch_y in train_loader:
        optimizer_dropout.zero_grad()
        y_pred = model_dropout(batch_X)
        loss = criterion(y_pred, batch_y)
        loss.backward()
        optimizer_dropout.step()

    model_dropout.eval()
    with torch.no_grad():
        val_pred = model_dropout(X_val)
        val_loss = criterion(val_pred, y_val).item()

    print(f"Epoch {epoch+1}, Validation Loss: {val_loss:.4f}")

    early_stopping_dropout(val_loss, model_dropout)
    if early_stopping_dropout.early_stop:
        print("Early stopping triggered.")
        break

model_dropout.load_state_dict(torch.load('checkpoint.pt'))

# 3. ドロップアウトなし、L2 正則化あり
print("\n----- 3. ドロップアウトなし、L2 正則化あり -----")
model_l2 = nn.Linear(10, 1)
optimizer_l2 = optim.SGD(model_l2.parameters(), lr=0.01, weight_decay=0.01)  # L2 正則化
early_stopping_l2 = EarlyStopping(patience=3, verbose=True)

for epoch in range(50):
    model_l2.train()
    for batch_X, batch_y in train_loader:
        optimizer_l2.zero_grad()
        y_pred = model_l2(batch_X)
        loss = criterion(y_pred, batch_y)
        loss.backward()
        optimizer_l2.step()

    model_l2.eval()
    with torch.no_grad():
        val_pred = model_l2(X_val)
        val_loss = criterion(val_pred, y_val).item()

    print(f"Epoch {epoch+1}, Validation Loss: {val_loss:.4f}")

    early_stopping_l2(val_loss, model_l2)
    if early_stopping_l2.early_stop:
        print("Early stopping triggered.")
        break

model_l2.load_state_dict(torch.load('checkpoint.pt'))

# 4. ドロップアウトと L2 正則化あり
print("\n----- 4. ドロップアウトと L2 正則化あり -----")
model_both = ModelWithDropout(dropout_rate=0.5)
optimizer_both = optim.SGD(model_both.parameters(), lr=0.01, weight_decay=0.01)  # L2 正則化
early_stopping_both = EarlyStopping(patience=3, verbose=True)

for epoch in range(50):
    model_both.train()
    for batch_X, batch_y in train_loader:
        optimizer_both.zero_grad()
        y_pred = model_both(batch_X)
        loss = criterion(y_pred, batch_y)
        loss.backward()
        optimizer_both.step()

    model_both.eval()
    with torch.no_grad():
        val_pred = model_both(X_val)
        val_loss = criterion(val_pred, y_val).item()

    print(f"Epoch {epoch+1}, Validation Loss: {val_loss:.4f}")

    early_stopping_both(val_loss, model_both)
    if early_stopping_both.early_stop:
        print("Early stopping triggered.")
        break

model_both.load_state_dict(torch.load('checkpoint.pt'))

# 最終的な検証損失の比較
print("\n----- 最終的な検証損失の比較 -----")
model_no_reg.eval()
model_dropout.eval()
model_l2.eval()
model_both.eval()
with torch.no_grad():
    val_loss_no_reg = criterion(model_no_reg(X_val), y_val).item()
    val_loss_dropout = criterion(model_dropout(X_val), y_val).item()
    val_loss_l2 = criterion(model_l2(X_val), y_val).item()
    val_loss_both = criterion(model_both(X_val), y_val).item()

print(f"1. ドロップアウトと L2 正則化なし: {val_loss_no_reg:.4f}")
print(f"2. ドロップアウトあり、L2 正則化なし: {val_loss_dropout:.4f}")
print(f"3. ドロップアウトなし、L2 正則化あり: {val_loss_l2:.4f}")
print(f"4. ドロップアウトと L2 正則化あり: {val_loss_both:.4f}")
1. ドロップアウトと L2 正則化なし: 0.9787
2. ドロップアウトあり、L2 正則化なし: 0.7466
3. ドロップアウトなし、L2 正則化あり: 0.7747
4. ドロップアウトと L2 正則化あり: 0.6960

この結果により、Early StoppingにおいてドロップアウトとL2正則化のどちらの手法も相性が良いことがわかりました。

次の論文では最新のEarly Stoppingの手法について言及してみようと思います。

論文1：Progressive Early Stopping (PES)

Understanding and Improving Early Stopping for Learning with Noisy Labels
The memorization effect of deep neural network (DNN) plays a pivotal role in many state-of-the-art label-noise learning ...
arxiv.org
  • 層ごとに適応したEarly Stoppingを導入
    • この論文では、Progressive Early Stopping (PES) を提案し、層ごとに異なるエポック数で学習を調整します。これにより、各層が持つノイズへの感受性を考慮し、過学習を防ぎながらモデルの性能を向上させる手法を実現しました。
  • 実験を通じたPESの有効性の証明
    • CIFAR-10/100やClothing-1Mでの実験から、PESが分類性能を一貫して向上させることが確認されました。特に、ラベルノイズが多い環境でも、従来手法を超える安定した結果を達成しました。
  • ノイズを考慮した革新的なアプローチ
    • PESは、ネットワークの層ごとにノイズの影響を考慮し、過学習を防ぐ新しい視点を提供します。この手法により、ノイズが多いデータ環境でもモデルが効率よく収束し、高い性能を発揮できるようになります。

論文2：Early-Stopping Self-Consistency (ESC)

Escape Sky-high Cost: Early-stopping Self-Consistency for Multi-step Reasoning
Self-consistency (SC) has been a widely used decoding strategy for chain-of-thought reasoning. Despite bringing signific...
arxiv.org
  • ESCによる推論コストの大幅削減
    • ESCは、サンプリング中に早期停止を導入することで計算コストを大幅に削減する新しい手法です。MATHやGSM8Kといったタスクで、最大80%以上のコスト削減を実現しつつ、従来のSelf-Consistency (SC) と同等の精度を維持することが確認されました。
  • 動的制御スキームによる柔軟性
    • ESCでは、ウィンドウサイズや最大サンプリング数を動的に調整する制御スキームを採用しています。この仕組みにより、タスクごとにコストと性能のバランスを最適化し、さまざまな推論タスクやモデルへの適用性を向上させています。
  • 理論的保証に基づく信頼性
    • ESCは、早期停止による推論結果がSelf-Consistency (SC) と同等であることを確率的に保証します。例えば、ウィンドウサイズ8では誤差確率が2×10⁻³以下と極めて低く、精度を維持しながら効率的な推論を実現します。

論文3：

https://jmlr.org/papers/volume23/21-0983/21-0983.pdf?utm_source=chatgpt.com
jmlr.org
  • Early StoppingとTikhonov正則化の理論的関連性を解明
    • Early Stoppingによる学習プロセスが、Tikhonov正則化の学習過程と似た挙動を示すことを理論的に解明しました。さらに、どちらも同じ一般化誤差の上限を達成できることを証明しています。
  • データ依存型停止ルールの提案
    • Cross-validationを利用したデータ依存型の停止ルールを提案し、事前の知識がなくても最適な停止タイミングを決定可能にしました。この手法により、一般化誤差を効果的に抑えることができます。
  • 実験による手法の有効性の実証
    • CIFARなどのデータセットを用いた実験で、提案手法が既存の正則化パラメータを用いる方法と同等以上の性能を発揮することを確認しました。これにより、Early Stoppingの有効性が実証されました。
Early Stopping の派生手法と関連手法

Early Stoppingには他にも多くの種類があり、それぞれの場面に応じて使い分ける必要性があることがわかります。

手法名概要特徴適用例
Adaptive Early StoppingPatience や delta を動的に調整して停止条件を最適化。学習進行に応じた柔軟な停止。過学習防止、複雑な学習タスク。
Online Early Stopping検証データを使わず、訓練データの損失変化で判断。全データを訓練に使用可能。小規模データセットや検証データが確保できない場合。
Stochastic Early Stopping確率的に Early Stopping を適用。過早停止のリスクを軽減し、性能向上の可能性を探索。大規模モデルの学習。
Validation Loss Smoothing検証損失を移動平均などで平滑化。ノイズの多いデータでの Early Stopping 精度向上。ノイズが多いデータセットの学習。
Plateau Learning Rate Reduction with Early Stopping学習率を減少させても改善がない場合に停止。学習率スケジューリングと Early Stopping を統合。段階的に学習率を減少させるタスク。
Regularized Early Stopping停止時に正則化を適用して学習タイミングを調整。停止タイミングの柔軟性が向上。正則化が重要なモデル。
AutoML-Driven StoppingAutoML を用いて最適な停止条件を探索。自動化されたパラメータチューニング。AutoML を利用した大規模モデル学習。
Bayesian Early Stoppingベイズ推論に基づいて停止判断を行う。不確実性を考慮し、理論的に基づいた判断。不確実性が高いデータやモデル。
Lookahead Early Stopping仮想エポックで将来の学習状態を予測して停止。過学習と過早停止の両方を防止。長期的な学習が必要なタスク。
Ensemble Early Stopping複数の Early Stopping 条件を統合して判断。指標を統合することで堅牢な停止条件を実現。複数の指標が重要な学習プロセス。

学習の振り返りと次回予告

今回の学習では、モデルの効率化と性能向上に必要な基盤技術を体系的に学びました。ミニバッチ学習やバッチ正規化を活用した効率的な学習プロセスの構築に始まり、SGDやAdamといった最適化アルゴリズムの実践的な適用を深めました。また、データ拡張やL1/L2正則化、蒸留や枝刈りといった正則化手法や軽量化技術も網羅。さらに、Early Stoppingや量子化を用いた学習の制御と過学習の防止方法を習得しました。これらを組み合わせることで、汎化性能の向上や計算効率の最適化を目指すための基礎が固まりました。

次回は、畳み込みニューラルネットワーク（CNN）をテーマに、基本概念から応用までを体系的に学びます。まず、畳み込み演算やプーリングなどの基礎を理解した上で、PyTorchを用いたモデル構築と転移学習の実践に進みます。また、LeNet、AlexNet、ResNetなどの進化をたどり、それぞれの技術革新を学びます。これにより、CNNの理解を深め、画像認識などの応用分野に対するモデル設計スキルを向上させます。

次回も学びを深め、実践を通じてさらなる成長を目指しましょう！

コメント

タイトルとURLをコピーしました