概要
最近では私たちの生活のあらゆる場面でAIが密接に関わっています。その中核技術であるディープラーニング(深層学習) は、私たちが日常的に行っている無意識的な行動を意識化し、具体的なモデルとして具現化することに成功しています。たとえば、画像の中から人の顔を見つけたり、会話の文脈を理解して次に取るべき行動を推測するといった行動です。
これらの無意識的な行動がどのようにしてモデル化され、技術として現実世界に応用されているのかを学ぶことは、単なる技術者としての知識を得るだけでなく、「私たち自身の認知プロセスを深く理解する」という、人間的な進化に貢献する学びでもあります。
ディープラーニングを勉強するメリット
- 現代社会での競争力を高める
- ディープラーニングを学ぶことは、単なる技術の習得に留まりません。それは、私たちが直面するさまざまな問題を新たな視点から解決する力を与えてくれます。現在、多くの業界でディープラーニングは標準的な技術として浸透しており、これを理解することは、競争力のあるスキルセットを構築するうえで欠かせません。
- AIを「使う側」から「作る側」へシフトする
- 多くの人がChatGPTなどのAIツールを日々活用していますが、それらの背後にある仕組みを理解することで、単にAIを利用するだけでなく、自ら新しいAIモデルを設計し、応用する立場に立つことができます。これにより、「AIを使いこなすユーザー」から「AIを作り出すクリエイター」へと成長することができます。
- 問題解決能力の向上
- ディープラーニングの学びは、「問題を分解し、それを解決するためのモデルを設計する」というプロセスを自然と鍛えます。このアプローチは、AIに限らず、複雑な課題に対処するためのフレームワークとして役立ちます。
- データを「見る目」が養われる
- ディープラーニングは「データ駆動型の意思決定」を可能にする技術です。データを効果的に扱い、その中に隠されたパターンを見つける能力を養うことで、あらゆる分野での洞察力を向上させることができます。
- 社会に貢献できる技術を開発する力がつく
- ディープラーニングの応用は、医療、教育、交通、環境保護など、さまざまな分野にわたります。この学びを通じて、社会に価値を提供する技術を生み出す力を身につけることができます。
ディープラーニングの重要性と応用例
重要性:
- 高精度な予測:複雑な非線形関係を学習できるため、高い精度での予測が可能。
- ビッグデータの活用:大量のデータから有用なパターンを抽出。
応用例:
- 画像認識:物体検出、顔認識、自動運転車の視覚システム。
- 音声認識:音声アシスタント、字幕生成。
- 自然言語処理:翻訳、チャットボット、感情分析。
今回の目標
ディープラーニングは、数学的な理論を基にしていますが、そのすべてを一度に理解する必要はありません。このブログでは、少しずつ理論と実践を結びつけながら進めていきます。まずはディープラーニングの土台を築き、その後にトレーニングや最適化の仕組みへと進みます。
ディープラーニングの背景と重要性を理解する
- ディープラーニングがなぜ重要で、どのように私たちの生活や社会を変えているのかを掘り下げます。
ニューラルネットワークの基本構造を学ぶ
- ディープラーニングの核となる「ニューラルネットワーク」の構造を、具体的な例や数式を用いて解説します。
PyTorchの基本操作を習得する
- 実際に手を動かしながら、ディープラーニングモデルを構築するための基礎技術を身につけます。
ディープラーニングとは?
ディープラーニングは、多層のニューラルネットワークを用いてデータから特徴を自動的に学習する手法です。従来の機械学習では特徴量の設計(Feature Engineering)が必要でしたが、ディープラーニングではこのプロセスを自動化できます。
ニューラルネットワークとは?
ニューラルネットワークは、人間の脳をモデルにした情報処理手法です。人間の脳は無数のニューロン(神経細胞)が相互に結びつき、ネットワークを形成しています。ニューラルネットワークもこのように、ニューロンを模倣して構築された数値的なモデルです。ディープラーニングのニューラルネットワークは、ニューロンの接続(シナプス)や発火のメカニズムを模して、複雑な情報処理を行います。

ニューロンの構造とその役割
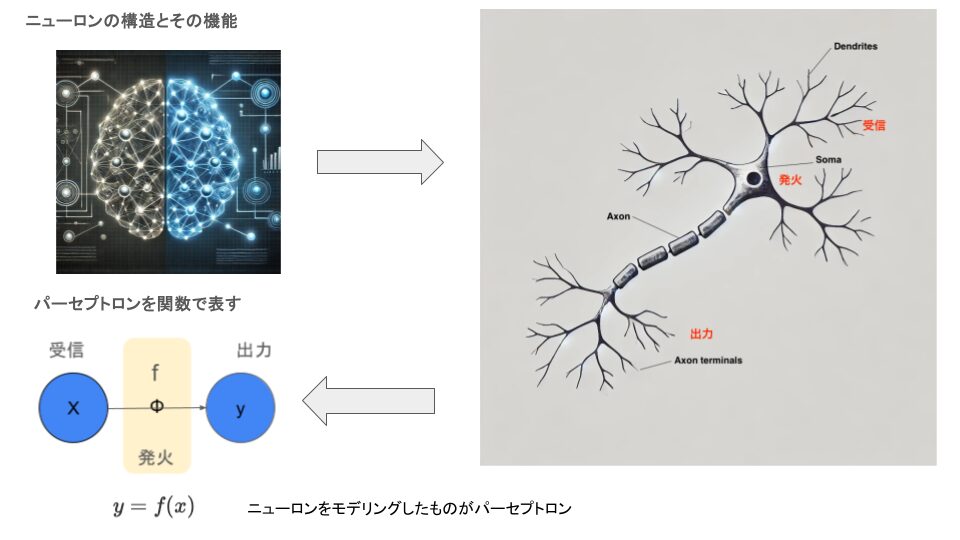
| 部位 | 名称(英語) | 役割 | 説明 |
|---|---|---|---|
| 細胞体 | Soma | 情報の統合 | 他のニューロンから受け取った信号を処理し、次に発火するかどうかを決定する中心部分。 |
| 樹状突起 | Dendrites | 他のニューロンからの信号を受信 | 枝状の構造を持ち、シナプスを介して他のニューロンから入力された信号をSomaに送る。 |
| 軸索 | Axon | 電気信号を他のニューロンや細胞に伝達 | Somaで生成された活動電位を、長い構造を通じてAxon Terminalまで運ぶ。 |
| 軸索末端 | Axon Terminal | 他のニューロンや細胞に信号を伝達(シナプスを形成) | 神経伝達物質を放出し、他のニューロンや細胞に信号を渡す役割を果たす。 |
| ニューロン全体 | Neuron | 脳や神経系での情報処理・伝達を担う神経細胞 | 複数のニューロンが相互に接続し、情報の受信、処理、送信を行い、神経ネットワークを形成する。 |
ニューラルネットワークの流れ
ニューラルネットワークは、人間の脳の構造を模倣して作られた情報処理モデルです。脳のニューロンが樹状突起で信号を受け取り、細胞体で統合し、軸索を通じて他の細胞へ伝達するように、ニューラルネットワークも入力層で情報を受け取り、隠れ層で処理し、出力層で結果を生成します。
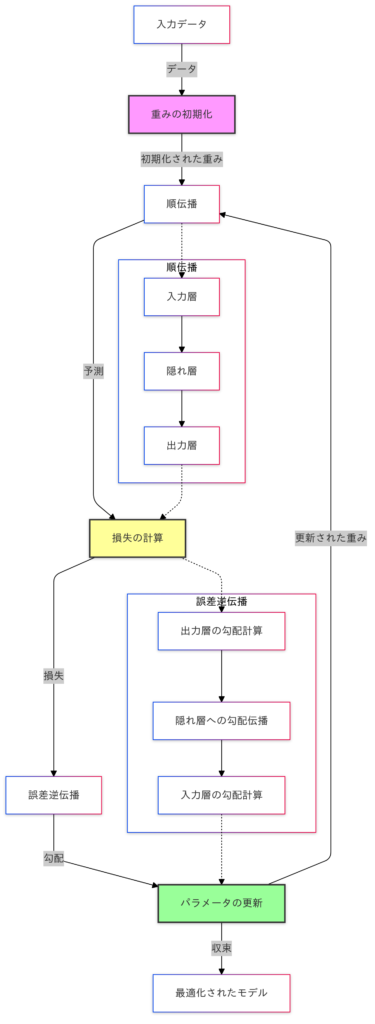
- 入力データ: モデルのトレーニングは、入力データの提供から始まります。
- 重みの初期化: ネットワーク内のパラメータ(重みとバイアス)がランダムに初期化されます。
- 順伝播: データは、入力層から隠れ層、出力層へと伝播され、予測値が生成されます。
- 損失の計算: 予測値と実際の値との差異(損失)を計算します。
- 誤差逆伝播: 損失を基に勾配を計算し、誤差を出力層から入力層まで逆方向に伝播します。
- パラメータの更新: 勾配を用いて重みを更新し、モデルを最適化します。
このプロセスを繰り返すことで、モデルは徐々に精度を向上させ、最適化されたネットワークが得られます。この図は、ディープラーニングにおけるモデル学習の全体像を簡潔に示しています。
重みの初期化とは?
ニューラルネットワークは、ニューロン同士が結合する際に「重み」と呼ばれる数値を持ち、これが入力信号の重要性を決定します。
重みは、ニューロン間のシナプス強度に相当し、モデルが情報をどのように処理するかを左右します。
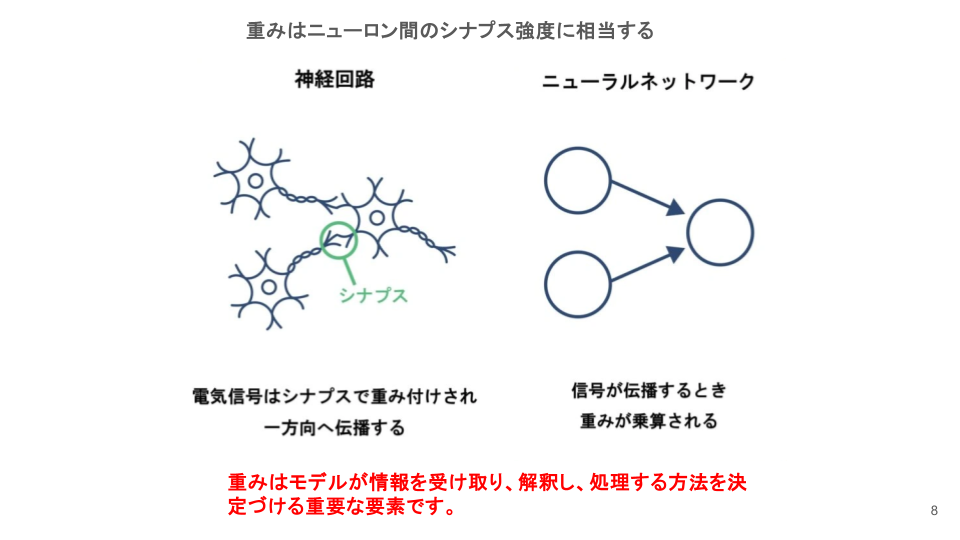
この重みは学習プロセスの中で更新されますが、学習開始時点での「初期値」を適切に設定することが非常に重要です。
なぜ重みの初期化が必要なのか?
重みの初期化は学習の出発点を決める重要な工程です。不適切な初期値では学習が停滞する可能性があります。例えば、すべての重みをゼロにすると各ニューロンの出力や勾配が同一になり、「対称性の破れ」が起こり学習が進みません。ランダムな初期化でこの問題を防ぎ、ニューロンが独立して学習できるようにします。
勾配消失問題
「対称性の破れ」の他に、主に深いネットワークで勾配が伝播する際に、値が小さくなりすぎたり(勾配消失問題)、大きくなりすぎたり(勾配爆発問題)して学習が不安定になることがあります。
初期化方法の工夫
ランダム初期化:
- 通常、標準正規分布や一様分布からサンプリングされた値を使用します。
- 例: $w \sim \mathcal{N}(0, 0.01)$(平均0、標準偏差0.01の正規分布)
深層学習では、勾配消失問題や勾配爆発問題などを避けるために、重みの分布を層の入力や出力の数に応じて以下のような調整を行います。
Xavier初期化
Xavier初期化は、シグモイドやtanh関数に適した手法で、入力信号と出力信号の分散を均一化することで中間層の出力を均一に保ち、学習の安定性を高めます。以下の条件を満たす際、入力と出力の分散が均一になります。
入力と出力の分散を均一にする:
$$\text{Var}(z^{(l)}) = \text{Var}(h^{(l-1)}) \cdot \frac{1}{n_{\text{in}}}$$
この数式は、ある層 $l$ の線形変換出力 $z^{(l)}$ の分散が、前の層の活性化 $h^{(l-1)}$ の分散と入力数 $n_{\text{in}}$ に依存することを表しています。
- $z(l)$ : 第$l$層の線形出力(活性化関数を通る前)。
- $h^{(l-1)}$ : 第 $l-1$層の出力。
- $n_{\text{in}}$ : 第$l$層の入力ユニットの数。
重みのサンプリング(一様分布):
$$w \sim \mathcal{U}\left(-\sqrt{\frac{6}{n_{\text{in}} + n_{\text{out}}}}, \sqrt{\frac{6}{n_{\text{in}} + n_{\text{out}}}}\right)$$
- $n_{in}$:層への入力ユニット数。
- $n_{\text{out}}$:次の層の出力ユニット数。
この数式は、重み $w$ が一様分布 $\mathcal{U}$ に従って初期化されることを示しています。この一様分布は、ニューラルネットワークの層の入力数 $n_{\text{in}}$ と出力数 $n_{\text{out}}$ に基づいて範囲が決定されます。
Xavier 初期化の一様分布:
Xavier 初期化に使われる連続型一様分布の確率密度関数は以下のようになります。
$$f(w) =
\begin{cases}
\frac{1}{b-a}, & a \leq w \leq b, \\
0, & \text{otherwise}.
\end{cases}$$
- $a$ = $-\sqrt{\frac{6}{n_{\text{in}} + n_{\text{out}}}}$
- $b$ = $\sqrt{\frac{6}{n_{\text{in}} + n_{\text{out}}}}$
つまり、重み $w$ は範囲 $[-a, a]$ の中で均等な確率密度を持ちます。
連続一様分布を利用することで、初期の重みが大きすぎたり小さすぎたりする問題を防ぎ、活性化関数の勾配消失や勾配爆発を抑えることができます。
Xavier初期化(一様分布)を実装例:
import torch
import matplotlib.pyplot as plt
import seaborn as sns
# Xavier初期化に基づく重みの初期化を関数化
def xavier_uniform_initialization(tensor, n_in, n_out):
"""
Xavier初期化を適用する関数
tensor: 初期化するテンソル
n_in: 層への入力ユニット数
n_out: 層からの出力ユニット数
"""
# 初期化範囲を計算
limit = (6 / (n_in + n_out)) ** 0.5 # sqrt(6 / (n_in + n_out))
return torch.nn.init.uniform_(tensor, -limit, limit)
# サンプルネットワークの重みを初期化
n_in = 128 # 入力ユニット数
n_out = 64 # 出力ユニット数
weight_tensor = torch.empty((n_out, n_in)) # 初期化対象のテンソル (n_out, n_in)
# Xavier初期化の適用
xavier_uniform_initialization(weight_tensor, n_in, n_out)
# 初期化結果を確認
print("Xavier初期化後の重み:")
print(weight_tensor)
# 重みの分布をヒストグラムと確率密度関数として可視化
plt.figure(figsize=(10, 6))
# ヒストグラムのプロット
sns.histplot(weight_tensor.numpy().flatten(), bins=30, color='blue', kde=True, edgecolor='black', stat='density', label='ヒストグラム')
# 確率密度関数のプロット
sns.kdeplot(weight_tensor.numpy().flatten(), color='red', fill=True, alpha=0.3, label='確率密度関数')
plt.title('Xavier初期化後の重みの分布と確率密度関数')
plt.xlabel('重みの値')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()Xavier初期化後の重み:
tensor([[-9.2046e-02, -4.2581e-02, -1.6542e-01, ..., 2.6726e-02,
-9.5255e-02, 4.2232e-02],
[ 7.7613e-05, 1.1598e-01, 1.1007e-01, ..., -9.5217e-02,
-1.1582e-01, -5.0591e-03],
[ 6.0672e-02, 8.2822e-02, 3.3297e-02, ..., -2.0036e-02,
2.6855e-02, 1.3913e-02],
...,
[-7.5331e-02, -6.2286e-02, 8.4402e-02, ..., -1.6252e-01,
1.0049e-01, -8.0568e-02],
[-2.7799e-02, -2.3219e-02, 8.5104e-02, ..., 5.9276e-03,
2.7931e-02, 1.2908e-01],
[ 1.3436e-01, -4.6255e-02, -1.7400e-01, ..., -1.3519e-01,
2.7504e-03, -1.3196e-01]])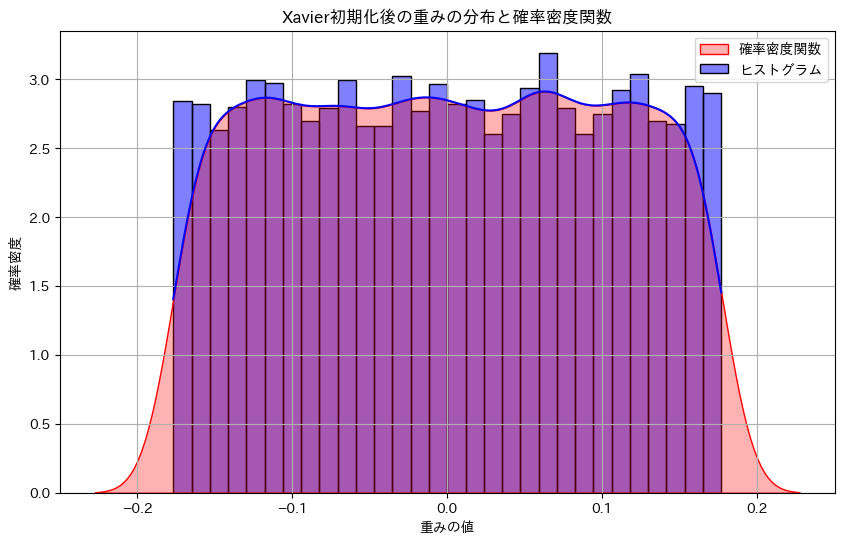
Seabornを使用してXavier初期化後の重みの分布をヒストグラムと確率密度関数として同時に可視化することで、Xavier初期化された重みの分布を視覚的に確認することができます。y軸の確率頻度とは、特定の範囲に属する重みの数を意味します。
重みのサンプリング(正規分布):
ここではXavierにおいて正規分布を使う方法を説明します。
$$W \sim \mathcal{N}\left(0, \sqrt{\frac{2}{n_{\text{in}} + n_{\text{out}}}}\right)$$
この数式は、重み $W$ が平均 0、分散 $\frac{2}{n_{\text{in}} + n_{\text{out}}}$ の正規分布 $\mathcal{N}$ に従って初期化されることを示しています。
Xavier初期化(正規分布)を実装例
import torch
import matplotlib.pyplot as plt
import seaborn as sns
# Xavier初期化に基づく重みの初期化を関数化(正規分布を使用)
def xavier_normal_initialization(tensor, n_in, n_out):
"""
Xavier初期化を適用する関数(正規分布を使用)
tensor: 初期化するテンソル
n_in: 層への入力ユニット数
n_out: 層からの出力ユニット数
"""
# 標準偏差を計算
std = (2 / (n_in + n_out)) ** 0.5 # sqrt(2 / (n_in + n_out))
return torch.nn.init.normal_(tensor, mean=0.0, std=std)
# サンプルネットワークの重みを初期化
n_in = 128 # 入力ユニット数
n_out = 64 # 出力ユニット数
weight_tensor = torch.empty((n_out, n_in)) # 初期化対象のテンソル (n_out, n_in)
# Xavier初期化の適用(正規分布を使用)
xavier_normal_initialization(weight_tensor, n_in, n_out)
# 初期化結果を確認
print("Xavier初期化後の重み(正規分布):")
print(weight_tensor)
# 重みの分布をヒストグラムと確率密度関数として可視化
plt.figure(figsize=(10, 6))
# ヒストグラムのプロット
sns.histplot(weight_tensor.numpy().flatten(), bins=30, color='blue', kde=True, edgecolor='black', stat='density', label='ヒストグラム')
# 確率密度関数のプロット
sns.kdeplot(weight_tensor.numpy().flatten(), color='red', fill=True, alpha=0.3, label='確率密度関数')
plt.title('Xavier初期化後の重みの分布と確率密度関数(正規分布)')
plt.xlabel('重みの値')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()Xavier初期化後の重み(正規分布):
tensor([[ 0.0528, -0.1805, -0.1454, ..., 0.0095, -0.0191, 0.0941],
[-0.1032, -0.1438, -0.0182, ..., -0.0957, 0.1128, -0.1012],
[ 0.0512, 0.0570, 0.1230, ..., -0.0012, -0.0156, 0.0857],
...,
[ 0.0335, -0.1638, -0.0096, ..., -0.1108, -0.0390, -0.0287],
[ 0.0785, -0.0187, 0.0980, ..., 0.0761, -0.0962, -0.0729],
[ 0.0899, 0.0165, -0.0513, ..., -0.0236, 0.0796, -0.2532]])
Xavier初期化における一様分布と正規分布の違い
- 一様分布は安全で一般的に利用されますが、深いネットワークでは正規分布が安定しやすいという結果が出ています。
| 基準 | 条件 | 推奨方法 | 理由 |
|---|---|---|---|
| ネットワークの深さ | 浅いネットワーク(数層) | 一様分布 | 勾配消失の影響が少なく、一様分布で十分に効果的。 |
| 深いネットワーク(多層) | 正規分布 | 勾配消失の影響が深刻になるため、正規分布を用いることで安定化が期待される。 | |
| 実験的判断 | 小規模なデータセット | 一様分布 | 過学習を防ぎやすい。 |
| 複雑または大規模なデータセット | 正規分布 | より複雑な特徴を捉えるため、正規分布が有効な場合が多い。 |
He初期化(Kaiming初期化)
He初期化は、ReLUやその派生関数(Leaky ReLUなど)に適した初期化法で、ReLUが入力の一部を0にするためXavier初期化では分散が小さくなりすぎる問題を補正し、分散を調整することで勾配の流れを安定化させます。
入力と出力の分散を均一にする:
$$\text{Var}(z^{(l)}) = \text{Var}(h^{(l-1)}) \cdot \frac{2}{n_{\text{in}}}$$
重みのサンプリング(一様分布):
$$w \sim \mathcal{U}\left(-\sqrt{\frac{6}{n_{\text{in}}}}, \sqrt{\frac{6}{n_{\text{in}}}}\right)$$
この数式は、重み $w$ が一様分布 $\mathcal{U}$ に従って初期化されます。この一様分布の範囲は、入力ユニット数 $n_{\text{in}}$ に基づいて決定されます。
He初期化に使われる連続型一様分布の確率密度関数は以下のようになります。
$$f(w) =
\begin{cases}
\frac{1}{b-a}, & a \leq w \leq b, \\
0, & \text{otherwise}.
\end{cases}$$
- $a$ = $-\sqrt{\frac{6}{n_{\text{in}}}}$
- $b$ = $\sqrt{\frac{6}{n_{\text{in}}}}$
He初期化(一様分布)を実装例
# He初期化に基づく重みの初期化を関数化
def he_uniform_initialization(tensor, n_in):
"""
He初期化を適用する関数(一様分布を使用)
tensor: 初期化するテンソル
n_in: 層への入力ユニット数
"""
# 初期化範囲を計算
limit = (6 / n_in) ** 0.5 # sqrt(6 / n_in)
return torch.nn.init.uniform_(tensor, -limit, limit)
# サンプルネットワークの重みを初期化
n_in = 128 # 入力ユニット数
n_out = 64 # 出力ユニット数
weight_tensor = torch.empty((n_out, n_in)) # 初期化対象のテンソル (n_out, n_in)
# He初期化の適用(一様分布を使用)
he_uniform_initialization(weight_tensor, n_in)
# 初期化結果を確認
print("He初期化後の重み(一様分布):")
print(weight_tensor)
# 重みの分布をヒストグラムと確率密度関数として可視化
plt.figure(figsize=(10, 6))
# ヒストグラムのプロット
sns.histplot(weight_tensor.numpy().flatten(), bins=30, color='green', kde=True, edgecolor='black', stat='density', label='ヒストグラム')
# 確率密度関数のプロット
sns.kdeplot(weight_tensor.numpy().flatten(), color='orange', fill=True, alpha=0.3, label='確率密度関数')
plt.title('He初期化後の重みの分布と確率密度関数(一様分布)')
plt.xlabel('重みの値')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()He初期化後の重み(一様分布):
tensor([[ 0.1134, -0.0493, 0.2052, ..., 0.0169, -0.0567, -0.1971],
[ 0.0924, -0.1315, -0.0893, ..., 0.1797, -0.1422, 0.0508],
[ 0.2132, 0.1177, 0.0513, ..., -0.0365, -0.0811, 0.0186],
...,
[ 0.2105, -0.1892, 0.1304, ..., -0.0428, 0.0546, -0.1464],
[ 0.1346, 0.0950, -0.1111, ..., -0.0734, 0.2068, -0.0941],
[-0.1634, 0.0464, -0.1916, ..., 0.0514, -0.1812, 0.0005]])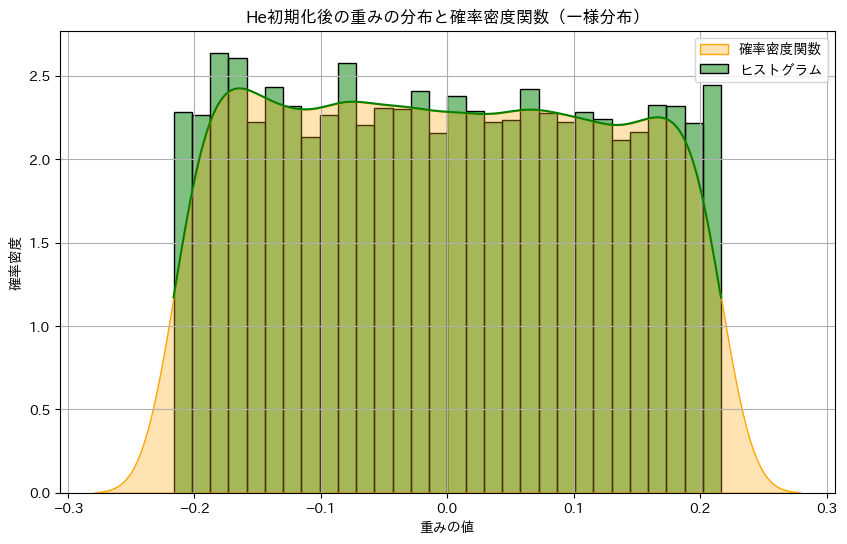
重みのサンプリング(正規分布):
$$W \sim \mathcal{N}\left(0, \sqrt{\frac{2}{n_{\text{in}}}}\right)$$
この数式は、重み $W$ が平均 0、分散 $\frac{2}{n_{\text{in}}}$ の正規分布 $\mathcal{N}$ に従って初期化されることを示しています。
He初期化に使われる正規分布の確率密度関数は以下のようになります。
$$f(w) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{w^2}{2\sigma^2}\right)$$
- μ = 0
- $σ$ = $\sqrt{\frac{2}{n_{\text{in}}}}$
He初期化(正規分布)の実装例
# He初期化に基づく重みの初期化を関数化(正規分布を使用)
def he_normal_initialization(tensor, n_in):
"""
He初期化を適用する関数(正規分布を使用)
tensor: 初期化するテンソル
n_in: 層への入力ユニット数
"""
# 標準偏差を計算
std = (2 / n_in) ** 0.5 # sqrt(2 / n_in)
return torch.nn.init.normal_(tensor, mean=0.0, std=std)
# サンプルネットワークの重みを初期化
n_in = 128 # 入力ユニット数
n_out = 64 # 出力ユニット数
weight_tensor = torch.empty((n_out, n_in)) # 初期化対象のテンソル (n_out, n_in)
# He初期化の適用(正規分布を使用)
he_normal_initialization(weight_tensor, n_in)
# 初期化結果を確認
print("He初期化後の重み(正規分布):")
print(weight_tensor)
# 重みの分布をヒストグラムと確率密度関数として可視化
plt.figure(figsize=(10, 6))
# ヒストグラムのプロット
sns.histplot(weight_tensor.numpy().flatten(), bins=30, color='purple', kde=True, edgecolor='black', stat='density', label='ヒストグラム')
# 確率密度関数のプロット
sns.kdeplot(weight_tensor.numpy().flatten(), color='blue', fill=True, alpha=0.3, label='確率密度関数')
plt.title('He初期化後の重みの分布と確率密度関数(正規分布)')
plt.xlabel('重みの値')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()He初期化後の重み(正規分布):
tensor([[-0.0727, -0.0463, -0.1358, ..., -0.3375, 0.1655, -0.0338],
[-0.0882, -0.1334, 0.1423, ..., -0.0485, -0.0710, 0.1205],
[-0.0437, 0.1516, -0.0595, ..., -0.1571, -0.1743, -0.0263],
...,
[-0.0596, -0.0911, 0.1415, ..., 0.0087, 0.0731, -0.1616],
[-0.0588, -0.0329, 0.0759, ..., -0.0888, -0.3038, -0.1678],
[-0.0091, -0.0336, -0.0639, ..., -0.1808, -0.0452, -0.0137]])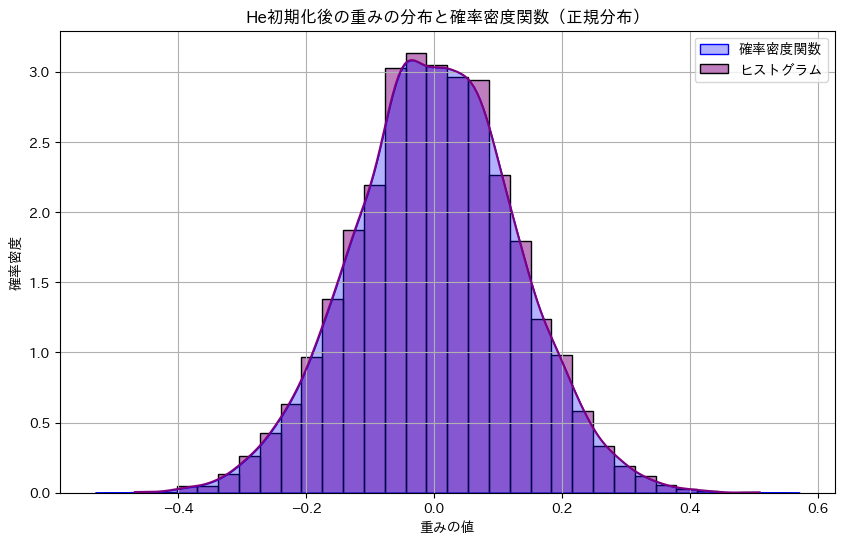
He初期化の一様分布と正規分布の違い:
| 特徴 | 一様分布 | 正規分布 |
|---|---|---|
| 初期化範囲/分散 | $[-√(6 / n_in), √(6 / n_in)]$ | 平均 0、分散 $2 / n_in$ |
| 重みの分布 | 均等な確率密度で重みを分布させる | 中央集中型の分布で重みを分布させる |
| 利用シーン | 浅いネットワークや単純なモデルに適用 | 深いネットワークや複雑なモデルに適用 |
| メリット | 計算が簡単で一様に初期化できる | ReLUの非線形性に適合しやすく、勾配消失を防ぐ |
| デメリット | 大きなネットワークでは安定性が低下する可能性 | 初期化範囲が広がりすぎると勾配爆発のリスクがある |
条件における使い分け:
| 基準条件 | 推奨方法 | 理由 |
|---|---|---|
| ネットワークの深さ | 深いネットワーク(多層) | ReLUの特性に合わせて分散を適切にスケーリングし、勾配消失を防ぐため |
| ネットワークの深さ | 浅いネットワーク(数層) | 一様分布でも十分に効果的であり、計算が簡単なため |
| データセットの規模 | 小規模なデータセット | 一様分布で過学習を防ぎやすい |
| データセットの規模 | 複雑または大規模なデータセット | 正規分布の方が複雑な特徴を捉えるのに有効な場合が多い |
He初期化の利点:
- 勾配消失の軽減:ReLUの非線形性により、負の部分がゼロになる特性を持つため、分散のスケーリングを適切に行うことで勾配消失問題を軽減します。
- 学習の安定性向上:初期化時に適切な分散を保つことで、学習過程が安定しやすくなります。
- 深いネットワークへの適用:深層学習モデルにおいて、特に深いネットワークで有効です。
全結合層におけるHe初期化の実装例(一様分布)
import torch
import torch.nn as nn
# ネットワークの例
class SampleNet(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SampleNet, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, output_size)
# He初期化を適用(一様分布)
nn.init.kaiming_uniform_(self.fc1.weight, nonlinearity='relu')
nn.init.kaiming_uniform_(self.fc2.weight, nonlinearity='relu')
nn.init.zeros_(self.fc1.bias)
nn.init.zeros_(self.fc2.bias)
def forward(self, x):
out = self.fc1(x)
out = self.relu(out)
out = self.fc2(out)
return out
# モデルの初期化
input_size = 128
hidden_size = 64
output_size = 10
model = SampleNet(input_size, hidden_size, output_size)
# 初期化された重みの確認
print("He初期化後の重み(fc1):")
print(model.fc1.weight)
print("He初期化後の重み(fc2):")
print(model.fc2.weight)重みの初期化の必要性
適切な重み初期化は、ニューラルネットワークの学習を安定化し、勾配消失や爆発を防ぎます。Xavier初期化はシグモイドやtanhに適し、各層の分散を均一に保ちます。一方、He初期化はReLUに最適で、深いネットワークでも勾配消失を抑え、効率的な学習を可能にします。これにより、モデルの性能と収束速度が向上します。
多層パーセプトロン(MLP)
多層パーセプトロン(MLP)は、ディープラーニングでよく使われるニューラルネットワークの一つです。MLPは、入力層、複数の隠れ層(中間層)、出力層で構成されており、これらの層を通じてデータの非線形な特徴を学習します。ここで、各層に存在する「ニューロン」は、脳の神経細胞を模した計算単位であり、他のニューロンからの入力を加重し、活性化関数を用いて次の層へ信号を渡します。
MLPでは、入力層がデータを受け取り、隠れ層でそのデータの中にある重要なパターンや特徴を抽出します。最終的に出力層で目的に応じた結果を得る(例えば、分類や予測)という流れです。
MLPの構造と動作
- 入力層 :
- 最初にデータを受け取る部分で、入力データの各特徴が個別のニューロンに対応します。例えば、画像の場合は各ピクセルの値が入力として使用されます。
- 隠れ層(Hidden Layer):
- 入力層からの情報を処理し、より高度な特徴を学習する層です。隠れ層はニューロンが複数の重み付き入力を受け取り、その合計に活性化関数を適用して出力を生成します。隠れ層が多くなるほど、モデルはより複雑で高度な特徴を捉えることが可能です。
- 出力層 :
- モデルの最終的な予測を出力する層です。例えば、画像分類であれば、クラスの数に応じたニューロンが配置され、その中からどのクラスに属するかを確率的に示します。
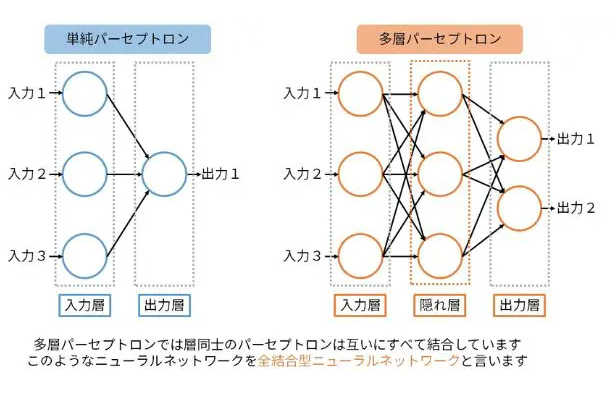
パーセプトロンは、ニューラルネットワークの基本単位であり、線形分類器です。
入力ベクトルを$\mathbf{x} = [x_1, x_2, …, x_n]$、重みベクトルを$\mathbf{w} = [w_1, w_2, …, w_n]^\top$、バイアスを$b$とすると、出力$y$は以下で表されます。
$$y = f(z) = f(\mathbf{w}^\top \mathbf{x} + b)$$
- $f(z)$ は活性化関数を用いた変換
- $z$ は、入力の線形結合の結果を指し、活性化関数を適用する前の中間的な値です。この $z$ を入力として、活性化関数 $f$ により非線形変換が行われ、最終的な出力 $y$ が得られます。
隠れ層を増やす利点
- 複雑なパターンの学習:隠れ層が増えることで、データの複雑な非線形関係を学習可能。
- 表現力の向上:深いネットワークはより高度な特徴を自動的に抽出。
活性化関数
隠れ層の各ニューロンは、活性化関数を用いてその出力を変換します。活性化関数は、脳のニューロンが情報を発火するかしないかを模倣しています。

ディープラーニングでよく使われる活性化関数には以下のようなものがあります。
ReLU関数
$$f(z) = \max(0, z)$$
特徴:
入力が正ならそのまま、負なら0を返す関数。計算が単純で勾配消失問題を軽減できるため、よく用いられます。
用途:
中間層の活性化関数として主に使用され、特に深層ニューラルネットワークでよく用いられます。
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# PyTorchを使ってReLU関数を定義する
relu = nn.ReLU()
# GPUが利用可能かどうかをチェック
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# x値の生成 (GPUに移動)
x = torch.linspace(-10, 10, 100).to(device)
# ReLU関数をxに適用
y_relu = relu(x)
# Plotting
plt.figure(figsize=(15, 5))
# ReLU plot (CPUに戻してからNumPyに変換)
plt.subplot(1, 3, 2)
plt.plot(x.cpu().detach().numpy(), y_relu.cpu().detach().numpy(), label="ReLU", color="green")
plt.title("ReLU Function")
plt.xlabel("x")
plt.ylabel("ReLU(x)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()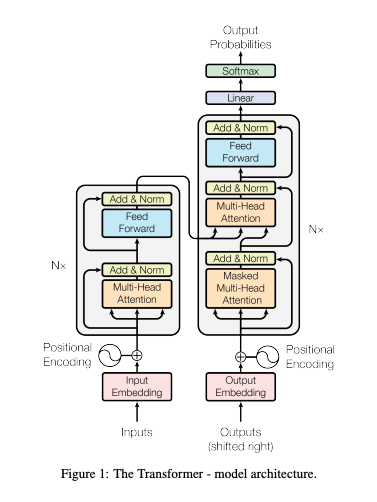
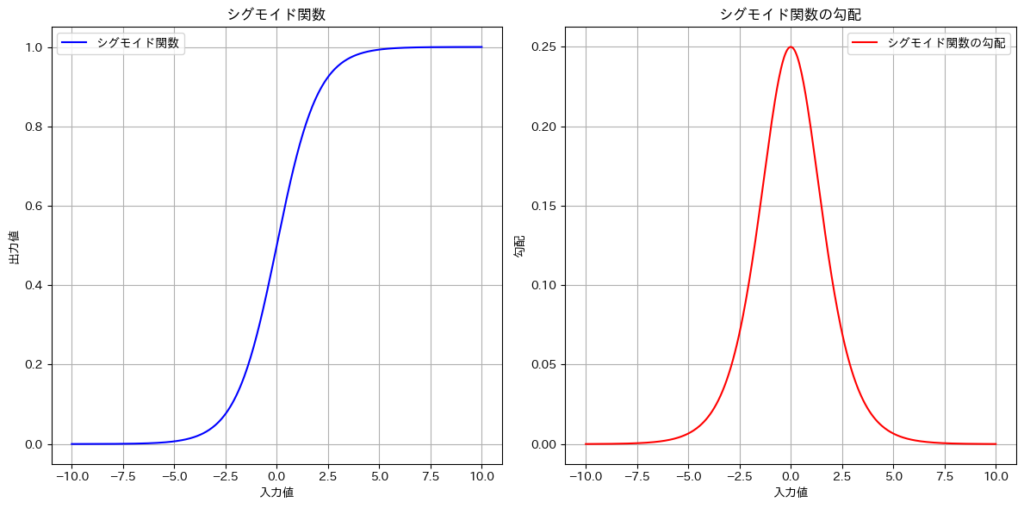
シグモイド関数
$$\sigma(z) = \frac{1}{1 + e^{-z}}$$
特徴:
入力を0から1の範囲に変換するため、特に確率のような出力を必要とする場合に使用されますが、勾配消失問題の影響を受けやすいです。
用途:
シグモイド関数は、主に二値分類タスクにおいて出力を確率として解釈するために使用されます。一方、シグモイド関数は隠れ層で完全に使われなくなったわけではありませんが、現在のディープラーニングでは効率や学習性能の面で優れるReLUやtanhが主流となっています。
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# シグモイド関数を定義する
sigmoid = nn.Sigmoid()
# GPUが利用可能かどうかをチェック
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# x値の生成 (GPUに移動)
x = torch.linspace(-10, 10, 100).to(device)
# 各関数のy値を計算する
y_sigmoid = sigmoid(x)
# Plotting
plt.figure(figsize=(15, 5))
# Sigmoid plot (CPUに戻してからNumPyに変換)
plt.subplot(1, 3, 1)
plt.plot(x.cpu().detach().numpy(), y_sigmoid.cpu().detach().numpy(), label="Sigmoid", color="blue")
plt.title("Sigmoid Function")
plt.xlabel("x")
plt.ylabel("sigmoid(x)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()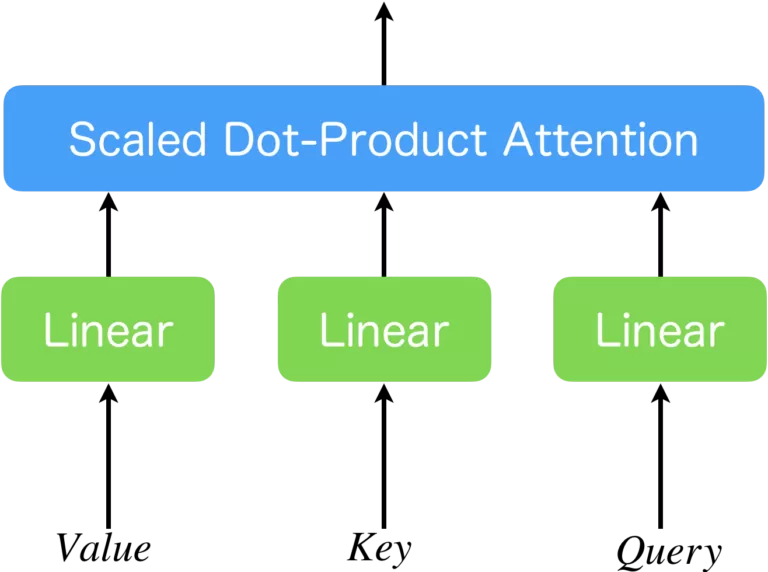
tanh関数
$$\tanh(z) = \frac{e^{z} + e^{-z}}{e^{z} – e^{-z}}$$
特徴:
出力が-1から1の範囲に収まり、シグモイド関数に似ていますが、より広い出力範囲を持つため、勾配消失の影響が若干少なくなります。出力がゼロ中心になるため、学習の収束が速くなることが期待できます。
用途:
回帰や分類タスクの隠れ層で使用されることが多いです。シグモイド関数よりも安定した学習が行われることが多く、LSTMなどのリカレントニューラルネットワーク(RNN)のゲート部分でも用いられます。
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# PyTorchを使ってtanh関数を定義する
tanh = nn.Tanh()
# GPUが利用可能かどうかをチェック
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# x値の生成 (GPUに移動)
x = torch.linspace(-10, 10, 100).to(device)
# tanh関数をxに適用
y_tanh = tanh(x)
# Plotting
plt.figure(figsize=(15, 5))
# tanh plot (CPUに戻してからNumPyに変換)
plt.subplot(1, 3, 3)
plt.plot(x.cpu().detach().numpy(), y_tanh.cpu().detach().numpy(), label="tanh", color="purple")
plt.title("Tanh Function")
plt.xlabel("x")
plt.ylabel("tanh(x)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()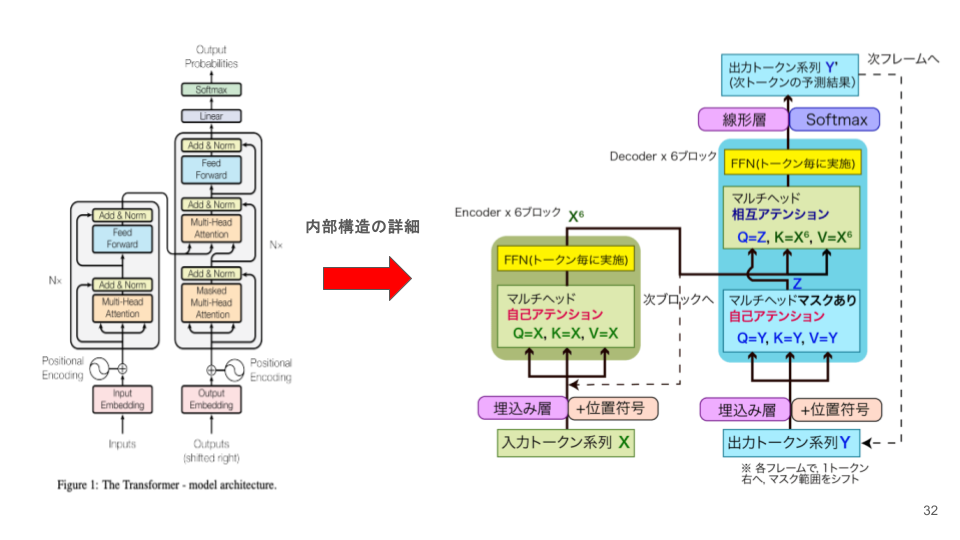
ソフトマックス関数
$$\sigma(z)_i = \frac{e^{z_i}}{\sum_{j=1}^{N} e^{z_j}}$$
- $z_i$ は入力ベクトル $\mathbf{z} = [z_1, z_2, \dots, z_N]$ の $i$ 番目の要素です。
- $e^{z_i}$ は、自然対数の底 $e$ を基にした指数関数です。
- ソフトマックス関数は、入力ベクトル全体に適用され、それぞれの $z_i$ に対応する「確率」を返します。
この数式により、すべてのクラスが相対的な重要度を持ち、確率の形で出力されます。これにより、多クラス分類問題に適した確率分布を生成します。
また、ソフトマックス関数はシグモイド関数の一般化であり、その詳細は以下のURLで説明されています。

特徴:
- 確率の出力:
- ソフトマックス関数は出力を0から1の範囲に正規化し、合計を1にすることで、各出力を「特定のクラスに属する確率」として解釈可能にします。
- 正規化:
- 入力ベクトルの値を指数関数で正規化することで、負の値や大きな値も確率として解釈可能な相対的な重要度に調整されます。
- 区別能力:
- 最も高い出力値を持つクラスが選ばれることで、モデルの選択が明確になり、各クラスに対する確信度も把握できます。
用途:
- ニューラルネットワークの分類問題において、特に多クラス分類の出力層でよく用いられる活性化関数です。
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
# softmax関数を定義する
def softmax(x):
# PyTorchのsoftmax関数を使用
return F.softmax(x, dim=0)
# GPUが利用可能かどうかをチェック
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# x値の生成
x = torch.linspace(-10, 10, 100).to(device)
# softmax関数の値を生成する(離散的な点を使用)
y_softmax = softmax(x)
# ソフトマックス関数の出力の総和を確認
sum_softmax = y_softmax.sum().item()
print(f"Sum of softmax outputs: {sum_softmax}")
# プロットの作成
plt.figure(figsize=(7, 5))
# softmax関数のプロット
plt.plot(x.cpu().detach().numpy(), y_softmax.cpu().detach().numpy(), label="softmax", color="blue")
plt.title("Softmax Function")
plt.xlabel("x")
plt.ylabel("softmax(x)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()Sum of softmax outputs: 1.0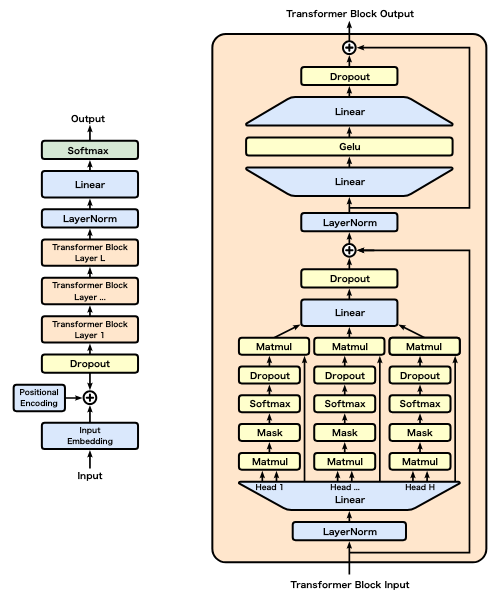
タスクと出力ユニットの違い
各タスクには異なる目的があるため、それに対応する出力ユニットも異なります。ここでは、回帰タスク、二値分類タスク、多値分類タスクにおける出力ユニットの違いや、それぞれに適した活性化関数と損失関数について説明します。
タスクと出力ユニットの対応表
| タスク | 出力値 | NN出力分布 | 出力ユニット | 活性化関数 | 損失関数 |
|---|---|---|---|---|---|
| 回帰 | 連続値 | ガウス分布 | 線形ユニット | 恒等関数 | 二乗誤差関数 (MSE) |
| 二値分類 | 確率 (0 から 1 の範囲) | ベルヌーイ分布 | シグモイドユニット | シグモイド関数 | バイナリークロスエントロピー関数 |
| 多値分類 | 各クラスの確率 | マルチヌーイ分布 | ソフトマックスユニット | ソフトマックス関数 | クロスエントロピー誤差関数 |
線形ユニット
線形ユニットは活性化関数が恒等関数で限界値がないため、勾配消失問題を防ぎつつ最適化手法と相性が良い特性を持ちます。
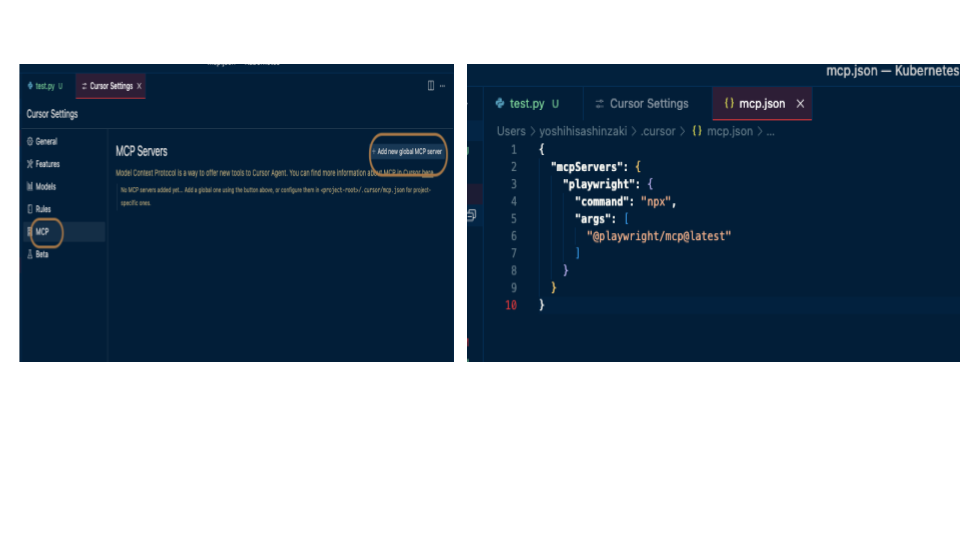
回帰問題における目的変数(連続値)の分布を「ガウス分布」と仮定し、線形ユニットを使って、「条件つきガウス分布」の平均を出力することが多い
線形ユニットの実装例
import torch
import torch.nn as nn
# 線形ユニット
linear_unit = nn.Identity()
input = torch.tensor([4.32], dtype=torch.float32)
output = linear_unit(input)
print("線形ユニットの出力:", output)線形ユニットの出力: tensor([4.3200])シグモイドユニット
二値分類問題では目的変数が二項分布に従うため、シグモイドユニットを用いてベルヌーイ分布を確率として出力します。
シグモイドユニットは、出力を0から1の範囲の確率として解釈するために採用されます。その背景には「オッズ」の概念があり、これは負例に対して正例が何倍起こりやすいかを表す比率($\frac{p}{1-p}$)として解釈されます。
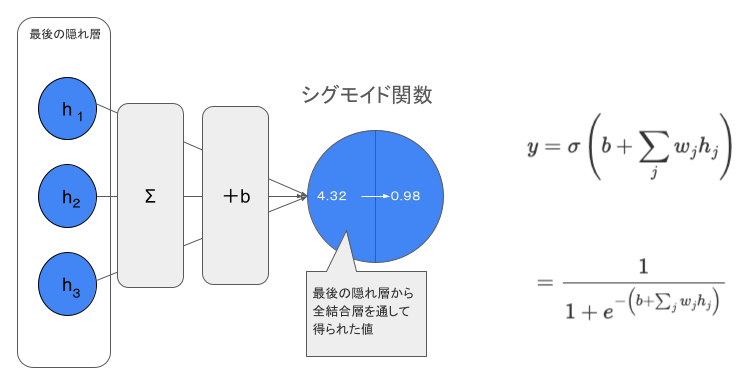
線形ユニットの実装例
# シグモイドユニット
sigmoid_unit = nn.Sigmoid()
input = torch.tensor([4.32], dtype=torch.float32)
output = sigmoid_unit(input)
print("シグモイドユニットの出力:", output)シグモイドユニットの出力: tensor([0.9869])オッズとシグモイド関数の関係
オッズは、正例の確率 $p$ と負例の確率 $1-p$ の比率として表されます。
$$オッズ = \frac{p}{1-p}$$
- このオッズを $e^z$ と対応づけることで、負例に対する正例が何倍起きやすいかを表現します。
正例の確率 $p$ はシグモイド関数 $\sigma(z)$ によって定式化することができる。
$$\frac{p}{1 – p} = e^z \\$$
$$p = e^z (1 – p) \\$$
$$p (1 + e^z) = e^z \\$$
$$p = \frac{e^z}{1 + e^z} = \sigma(z)$$
オッズと $z$ を関連づけることで、確率の範囲(0~1)内で正例と負例の比率を効率的に表現できます。
ソフトマックスユニット
ソフトマックスユニットは、活性化関数としてソフトマックス関数を用いる出力ユニットであり、多値分類問題では目的変数の多項分布に基づき、マルチヌーイ分布を出力します。

ソフトマックス関数はシグモイド関数の一般化であり、各入力値を $e^{z_i}$ に変換した後、全ての値の合計が1となるようにスケーリングします。
出力ユニットの実装例
# ソフトマックスユニット
softmax_unit = nn.Softmax(dim=0)
xs = torch.tensor([5.34, -1.32, 2.09], dtype=torch.float32)
ys = softmax_unit(xs)
print("ソフトマックスユニットの出力:", ys)ソフトマックスユニットの出力: tensor([0.9615, 0.0012, 0.0373]) # 総和が1になる損失関数
損失関数とは?
損失関数は、ニューラルネットワークが予測した値と実際の正解値の差を数値化し、その差を最小化することでモデルを最適化するための重要な要素です。
各出力ユニットに対応する損失関数は最尤推定に基づき、最適なパラメータ(重みやバイアス)を求める役割を果たします。
最尤推定とは?
最尤推定は、尤度関数が最大化されるようなパラメータを見つけることを目的とします。
- 尤度関数
- データ $X$ が与えられたとき、パラメータ $\theta$ がデータをどの程度「もっともらしく説明するか」を示します。
$$f(X∣θ)$$
$f(X∣θ$) : 尤度関数、$X$ : 観測データ、$\theta$ : 推定すべきパラメータ
具体例)犬と猫の画像を与えられた場合、尤度関数 $f(X|\theta)$ はそれが猫である確率を表す。
尤度の最大化とは?
尤度関数を最大化するパラメータ $\theta$ を探します。数学的には、以下を最大化する問題を解きます。
$$\theta_{\text{MLE}} = \arg\max_{\theta} f(X | \theta)$$
ここで、$f(X|\theta)$ が最大になるときの $\theta$ を「最尤推定値」と呼びます。
損失関数との関係は?
尤度関数を最大化する問題は、損失関数を最小化する問題と等価です。
$$最尤推定(対数尤度最大化)= 損失関数の最小化$$
- 尤度関数の対数を取り、負号を付けたものを損失関数とします。
$$L(\theta) = -\log f(\theta | X)$$
これにより、尤度最大化の代わりに、損失関数を最小化することで最尤推定を実現します。
線形ユニットの損失関数
線形ユニットでは、出力が目的変数(ターゲット)$t$ のガウス分布を仮定してモデル化されています。この仮定に基づき、ガウス分布の対数尤度最大化を行うことで、出力と目的変数の間の誤差を最小化することを目指します。その結果、ガウス分布の対数尤度最大化の問題は、平均二乗誤差 の最小化と等価になります。
線形ユニットは目的変数 ${t}$ のガウス分布をモデル化し、その対数尤度を最大化することは平均二乗誤差(MSE)の最小化と等価です。
ガウス分布の対数尤度を用いて損失関数を定義
- 尤度関数:ガウス分布に基づく確率密度関数 $N(t; y, I)$ は以下の形になります。
$$N(t; y, I) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left( -\frac{(t – y)^2}{2\sigma^2} \right)$$
- 損失関数:尤度の負の対数を取ることで損失関数を得ます。
$$L(\theta) = -\log N(t; y, I)$$
- 展開:ガウス分布の式を対数に代入し展開すると
$$L(\theta) = -\log \frac{1}{\sqrt{2\pi \sigma^2}} – \frac{(t – y)^2}{2\sigma^2}$$
第1項は定数項にまとめられ、第2項が損失の主要な部分を構成します。
$$L(\theta) = \frac{(t – y)^2}{2\sigma^2} + \text{const.}$$
- 最終的な損失関数:標準化された形では、二乗誤差として表現されます。
$$L(\theta) = (t – y)^2 + \text{const.}$$
- $t$ : 目的変数(正解値)
- $y$: ニューラルネットワークの出力値(予測値)
$$y=b+{W^T}{h}$$
- $b$ : バイアス項
- $W$ : 重み行列$h$ : 入力データ
- $h$ : 入力データ
- $σ2$ : ガウス分布の分散(定数として扱われる)
最適化の目的
- 損失関数 $L(\theta)$ を最小化することで、重み $W$ とバイアス $b$ を最適化します。このプロセスを「損失関数の最適化」と呼びます。
線形ユニットと損失関数の実装例
import torch
import torch.nn as nn
# 線形ユニット
linear_unit = nn.Identity()
input_linear = torch.tensor([[4.32]], dtype=torch.float32)
output_linear = linear_unit(input_linear)
print("線形ユニットの出力:", output_linear)
# 損失関数の定義
mse_loss_func = nn.MSELoss() # 平均二乗誤差
# 正解ラベル
target_linear = torch.tensor([[5.0]], dtype=torch.float32) # 線形ユニットの正解値
# 損失計算
loss_linear = mse_loss_func(output_linear, target_linear)
print("線形ユニットの損失:", loss_linear)線形ユニットの出力: tensor([[4.3200]])
線形ユニットの損失: tensor(0.4624)シグモイドユニットの損失関数
シグモイドユニットでは、出力が目的変数(ターゲット)$t$ のベルヌーイ分布を仮定してモデル化されています。この仮定に基づき、ベルヌーイ分布の対数尤度最大化を行うことで、出力と目的変数の一致を最大化することを目指します。その結果、ベルヌーイ分布の対数尤度最大化の問題は、バイナリークロスエントロピー誤差関数の最小化と等価になります。
ベルヌーイ分布の対数尤度を用いて損失関数を定義
- 尤度関数:
- 以下の数式はベルヌーイ分布の確率質量関数 (PMF) を表しており、観測値 $t∈{{0,1}}$ と成功確率 $y$ を示します。この式は、ベルヌーイ試行において観測された結果 $t$ の発生確率を計算するために用いられます。
$$\text{Bern}(t; y) = y^t (1 – y)^{1-t}$$
$y$ はモデルの出力、$t$ は目的変数(正解ラベル、0または1)。
- 損失関数:尤度の負の対数を取ることで損失関数を得ます。
$$L(\theta) = -\log \text{Bern}(t; y)$$
- 展開:ベルヌーイ分布の式を対数に代入し展開すると
$$L(\theta) = -\log \left( y^t (1 – y)^{1-t} \right)$$
- ログの性質を利用して分解:
$$L(\theta) = – \left[ t \log y + (1 – t) \log (1 – y) \right]$$
- 最終的な損失関数:
$$L(\theta) = – \left( t \log y + (1 – t) \log (1 – y) \right)$$
これは、バイナリークロスエントロピー誤差関数に一致します。
最適化の目的
- 損失関数 $L(\theta)$ を最小化することで、シグモイドユニットの重み $W$ とバイアス $b$ を学習します。
シグモイドユニットと損失関数の実装例
# シグモイドユニット
sigmoid_unit = nn.Sigmoid()
input_sigmoid = torch.tensor([[4.32]], dtype=torch.float32)
output_sigmoid = sigmoid_unit(input_sigmoid)
print("シグモイドユニットの出力:", output_sigmoid)
# 損失関数の定義
bce_loss_func = nn.BCELoss() # バイナリクロスエントロピー損失
# 正解ラベル
target_sigmoid = torch.tensor([[1.0]], dtype=torch.float32) # シグモイドユニットの正解値
# 損失計算
loss_sigmoid = bce_loss_func(output_sigmoid, target_sigmoid)
print("シグモイドユニットの損失:", loss_sigmoid)シグモイドユニットの出力: tensor([[0.9869]])
シグモイドユニットの損失: tensor(0.0132)シグモイド関数との関係
$$y = \sigma(z) = \frac{1}{1 + e^{-z}}, \quad z = b + \mathbf{W}^\top \mathbf{h}$$
$z$ は線形変換の結果であり、$b$ はバイアス、$W^T h$ は重み付き入力の和です。
損失関数 $L(\theta)$ をソフトプラス関数を使って表現できます。
$$L(\theta) = \log \left( 1 + e^{-(2t – 1)(b + \mathbf{W}^\top \mathbf{h})} \right)$$
ソフトプラス関数とは?
$$\text{softplus}(x) = \log(1 + e^x)$$
ソフトプラス関数は、シグモイド関数やReLU関数と関連があり、滑らかな非線形活性化関数としてニューラルネットワークで使用されることがあります。
シグモイド関数との役割の違い:
- シグモイド関数は、主に活性化関数として使用され、モデルの出力を0から1の確率に変換します。これにより、二値分類の結果として解釈できるようになります。
- ソフトプラス関数は活性化関数として使われることもありますが、特に勾配の計算やモデル出力を滑らかに変換する際に利用されます。ReLU関数の代替として用いられることが多く、ReLUの滑らかなバージョンと考えることができます。また、負の入力に対しても非ゼロの出力を持つ点が特徴です。
ソフトプラス関数
# ソフトプラスユニットの定義
softplus_unit = nn.Softplus()
# x値の生成
x_values = torch.linspace(-10, 10, 100)
# ソフトプラスユニットの出力を計算
y_values = softplus_unit(x_values)
# プロットの作成
plt.figure(figsize=(10, 5))
plt.plot(x_values.numpy(), y_values.detach().numpy(), label="Softplus", color="blue")
plt.title("Softplus Function")
plt.xlabel("Input")
plt.ylabel("Output")
plt.grid(True)
plt.legend()
plt.show()
ソフトマックスユニットの損失関数
ソフトマックスユニットでは、出力が目的変数(ターゲット)$t$ のマルチヌーイ分布を仮定してモデル化されています。この仮定に基づき、マルチヌーイ分布の対数尤度最大化を行うことで、出力と目的変数の一致を最大化することを目指します。その結果、マルチヌーイ分布の対数尤度最大化の問題は、クロスエントロピー誤差関数の最小化と等価になります。
マルチヌーイ分布の対数尤度を用いて損失関数を定義
- 尤度関数:
- この数式は、カテゴリ分布(Multinoulli分布)の確率質量関数 (PMF) を表しており、これは多項分布の特殊なケースです。ここで、$t_k$ はカテゴリ $k$ が発生したかを示すバイナリ変数($t_k \in \{0, 1\}$)、$y_k$ はカテゴリ $k$ に対応する確率を示しています。この分布は多クラス分類モデルでよく使用されます。
$$\text{Multinoulli}(t; y) = \prod_k y_k^{t_k}$$
$y_k$ : クラス $k$ の確率(モデルの出力)、$t_k$ : クラス $k$ に対応する正解ラベル(One-hot エンコーディング)
- 損失関数:尤度の負の対数を取ることで損失関数を得ます。
$$L(\theta) = -\log \text{Multinoulli}(t; y)$$
- 展開:マルチヌーイ分布の式を対数に代入し展開すると
$$L(\theta) = -\log \prod_k y_k^{t_k}$$
- 最終的な損失関数:
$$L(\theta) = -\sum_k t_k \log y_k$$
これは、クロスエントロピー誤差関数に一致します。
最適化の目的
損失関数 $L(\theta)$ を最小化することで、ソフトマックスユニットの重み $W$ とバイアス $b$ を学習します。
ソフトマックスユニットと損失関数の実装例
# Softmaxユニットの定義
softmax_unit = nn.Softmax(dim=1) # softmax関数の宣言
loss_func = nn.CrossEntropyLoss() # Cross Entropy Loss関数の宣言
# 入力例1
inputs = torch.tensor([[2.09, -1.30, 4.32]]) # 入力はクラスの値
labels = torch.tensor([0], dtype=torch.long) # inputsの答えとなるクラス
# 出力と損失計算
outputs = softmax_unit(inputs) # outputs取得
loss = loss_func(outputs, labels) # loss計算
print(outputs)
print(loss)
# 入力例2
inputs = torch.tensor([[2.09, -1.30, 4.32]]) # 入力はクラスの値
labels = torch.tensor([2], dtype=torch.long) # inputsの答えとなるクラス
# 出力と損失計算
outputs = softmax_unit(inputs) # outputs取得
loss = loss_func(outputs, labels) # loss計算
print(outputs)
print(loss)tensor([[0.0968, 0.0033, 0.9000]])
tensor(1.4215)
tensor([[0.0968, 0.0033, 0.9000]])
tensor(0.6183)ソフトマックス関数との関係
ソフトマックス関数は、各クラスのスコア $z_k$ を確率に変換します。
$$y_k = \text{softmax}^{(k)}(b + \mathbf{W}^\top \mathbf{h}) = \frac{\exp(z_k)}{\sum_j \exp(z_j)}$$
$z_k = b_k + W_k^T h$ : クラス$k$ のスコア(線形変換)
- $b_k$ : クラス $k$ のバイアス
- $W_k^T h$: クラス $k$ の重み付き入力
タスクに応じた出力ユニットと損失関数
上述で説明したそれぞれのタスクに応じた出力ユニットと損失関数のまとめです。
| タスク | 出力値 | NN出力分布 | 出力ユニット | 活性化関数 | 損失関数 | 損失関数の式 |
|---|---|---|---|---|---|---|
| 回帰 | 連続値 | ガウス分布 | 線形ユニット | 恒等関数 | 二乗誤差関数 (MSE) | $( (t – y)^2$ $+ \text{const.} )$ |
| 二値分類 | 確率 (0 から 1 の範囲) | ベルヌーイ分布 | シグモイドユニット | シグモイド関数 | バイナリークロスエントロピー関数 | $( – (t \log y + (1 – t) $$\log (1 – y)) )$ |
| 多値分類 | 各クラスの確率 | マルチヌーイ分布 | ソフトマックスユニット | ソフトマックス関数 | クロスエントロピー誤差関数 | $( – \sum_k t_k$$ \log y_k )$ |
順伝播の全体図
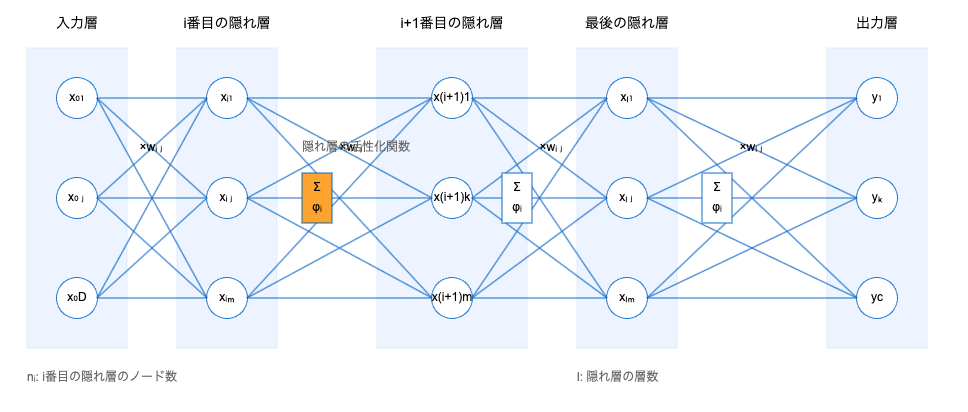
誤差逆伝播法と勾配降下法
誤差逆伝播法と勾配降下法は、ニューラルネットワークにおける学習プロセスの核となる技術で、人間の脳のニューロンにおけるシナプス強度の調整に相当します。ニューロンが繰り返し信号を受け取る中で、シナプスが適応していくように、誤差逆伝播法は損失を基に勾配を計算し、勾配降下法はその勾配を使って重み(接続強度)を最適化します。この仕組みにより、ネットワーク全体がより正確に情報を処理できるように進化していきます。

- 誤差逆伝播法(バックプロパゲーション)
- 誤差逆伝播法は、ニューラルネットワークの各パラメータ(重みやバイアス)の損失関数に対する偏微分(勾配)を効率的に計算するアルゴリズムです。この勾配情報を使って、勾配降下法による最適化を行います。
- 計算の流れ:
- バックプロパゲーションは、まず順伝播(フォワードパス)で入力データをネットワークに通し、出力と損失を計算します。その後、出力層から入力層へ向かって勾配を逆方向に伝播させます。
- チェーンルールの利用:
- 勾配の計算には微分のチェーンルールが用いられ、各層のパラメータに対する勾配が効率的に求められます。
- 計算の流れ:
- 誤差逆伝播法は、ニューラルネットワークの各パラメータ(重みやバイアス)の損失関数に対する偏微分(勾配)を効率的に計算するアルゴリズムです。この勾配情報を使って、勾配降下法による最適化を行います。
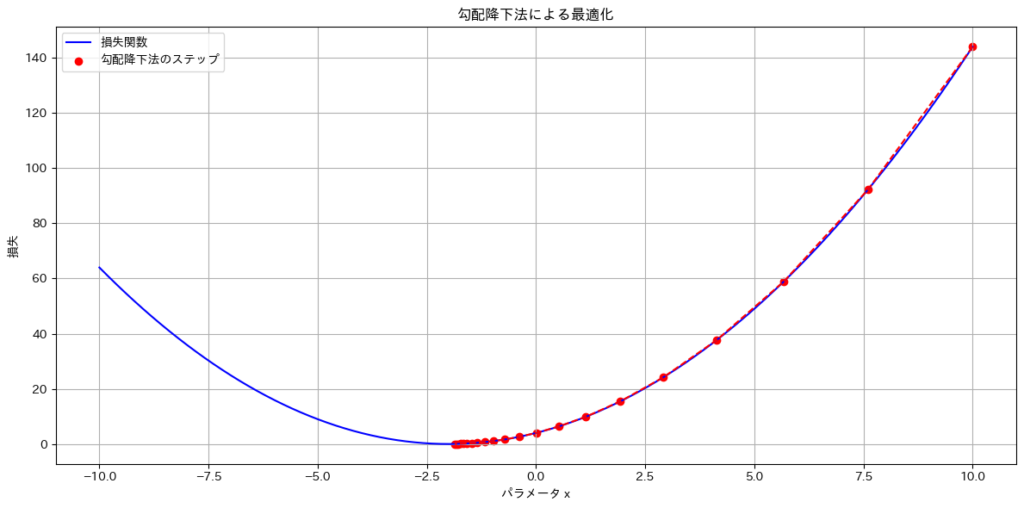
- 勾配降下法
- 勾配降下法 は、誤差逆伝播法によって計算された勾配を用いて逆向きにパラメータを更新し、損失関数を最小化するための最適化アルゴリズムです。
勾配とは?- 勾配とは、損失関数が各パラメータに対してどのように変化するかを示す値を並べたベクトルのことです。簡単に言うと、損失関数を最小化するために「どの方向にパラメータを動かせばいいか」を教えてくれる指針です。
- 勾配降下法 は、誤差逆伝播法によって計算された勾配を用いて逆向きにパラメータを更新し、損失関数を最小化するための最適化アルゴリズムです。
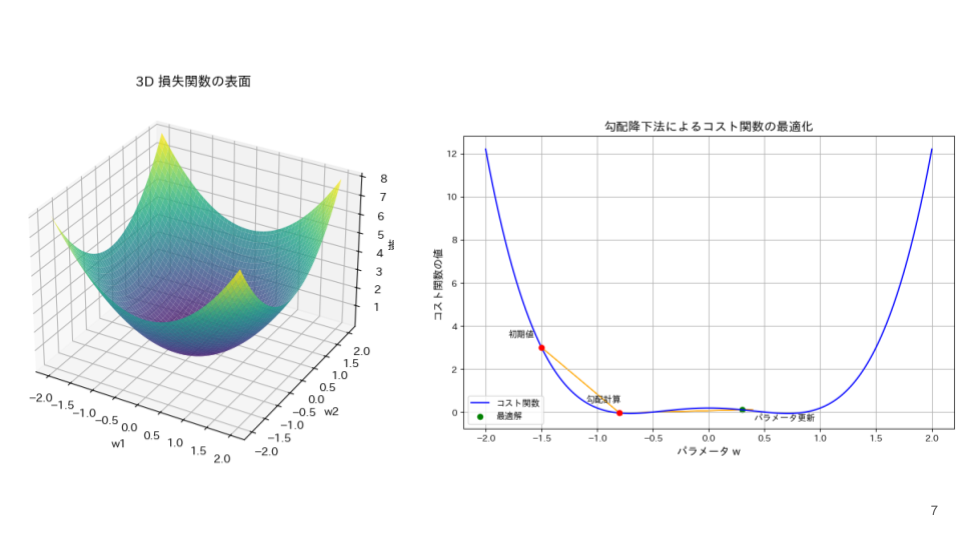
誤差逆伝播法と勾配降下法の役割の違い
誤差逆伝播法
- 勾配を効率的に計算する方法。
- 主にチェーンルールを用いて、出力層から入力層へ向かって誤差を伝播させながら勾配を計算する手法。
- 勾配計算が主な役割であり、パラメータの更新は行わない。
- 出力層での誤差を基に、その誤差が各層にどのように影響しているかをチェーンルール(連鎖律)を用いて逆方向に伝播させ、各パラメータの勾配を求める。
勾配降下法
- パラメータ$w$の初期値を決める。パラメータの初期値は、ランダムや特定の初期化方法(例: Xavier、He)で設定されます。勾配降下法では、この初期化された重みが学習の出発点となります。
- 計算された勾配を用いて損失関数を最小化する方向(負の勾配方向)にパラメータを更新するアルゴリズム。
- 勾配を利用し、損失関数の最小化に向けてパラメータを調整する。
微分の連鎖律(チェーンルール)とは?
微分の連鎖律は、複合関数(関数の中に関数が含まれる形)の微分を計算する際に用いる基本的な法則です。具体的には、関数 $y = f(g{(x)})$ のように、ある関数 $f$ が別の関数 $g$ によって構成されている場合に、その微分 $\frac{dy}{dx}$ を求める方法です。
複合関数 $y = f(g{(x)})$ の微分は、次のように計算できます。
$$\frac{dy}{dx} = \frac{dy}{dg} \cdot \frac{dg}{dx}$$
- $\frac{dy}{dg}$は関数 $f$ の $g$ に関する微分
- $\frac{dg}{dx}$は関数 $g$ の $x$ に関する微分です。
具体例)
例えば、関数 $y = \sin(3x + 2)$ の微分を考えます。この関数は $f(u) = \sin{(u)}$ と $g(x) = 3x + 2$ の複合関数として表せます。
- 内側の関数 $g(x)$ を微分:$\frac{dg}{dx}$
- 外側の関数 $f(u)$ を $u = g(x)$ で微分:$\frac{dy}{dg} = \cos(u) = \cos(3x + 2)$
- 連鎖律を適用:$\frac{dy}{dx} = \frac{dy}{dg} \cdot \frac{dg}{dx} = \cos(3x + 2) \cdot 3 = 3 \cos(3x + 2)$
ニューラルネットワークにおける連鎖律の応用
誤差逆伝播法(バックプロパゲーション)では、連鎖律を用いて出力層から入力層に向かって誤差の勾配を効率的に計算します。具体的には、各層の重みやバイアスに対する損失関数の偏微分を求める際に、連鎖律が不可欠です。

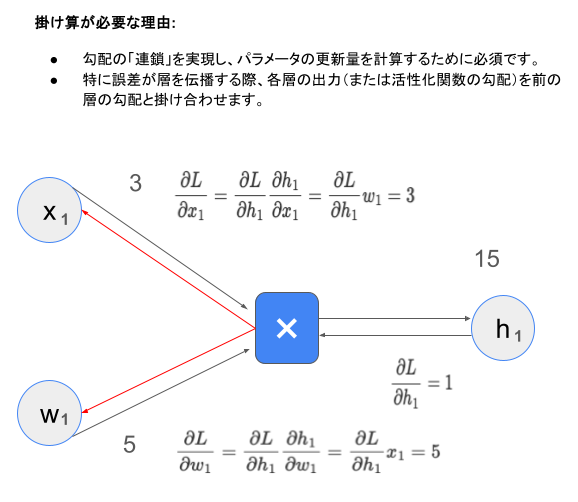
順伝播
- 入力 $x$ から出力 $y$ まで各層を通じて計算。
- 活性化関数に通して非線形性を加える。
- 掛け算:入力と重みのスケーリング(重み付き入力)に利用されます。この掛け算によって、入力の重要性が反映されます。
- 足し算:各ニューロンでは、入力信号 $x$ に対応する重み $w$ を掛け合わせた値を合計し、バイアス $b$ を加えます。
$z = \sum (w \cdot x) + b$
これはニューロンが次の層に渡す値(活性化関数の入力)を計算するプロセスです。
逆伝播
- 損失 $L$ から出力層を逆方向に辿り、各重み $w$ に対する $\frac{\partial L}{\partial w}$ を連鎖律を用いて計算。
- 出力層から誤差を計算し、連鎖律を使って各層の勾配を掛け算で伝播。
- 各層の勾配を利用して重みとバイアスを更新。
ニューラルネットワークにおけるAffine変換
Affine変換は、ニューラルネットワークの基礎的な構造であり、入力データを線形変換と平行移動によって変換します。この変換は、特徴量の抽出やデータの変形に重要な役割を果たしますが、非線形性を持たないため、活性化関数と組み合わせて使用されます。
$$z=Wx+b$$
Affine変換の役割
線形結合:
- 各入力に重みを掛けて足し合わせる操作を意味します。
- ニューラルネットワークにおける特徴量の重要性を学習します。
平行移動:
- バイアスを加えることで、入力の分布がゼロに近い範囲からズレている場合でも適切に処理できます。
- 活性化関数(ReLUなど)の非線形変換を適切に動作させるための調整として機能します。
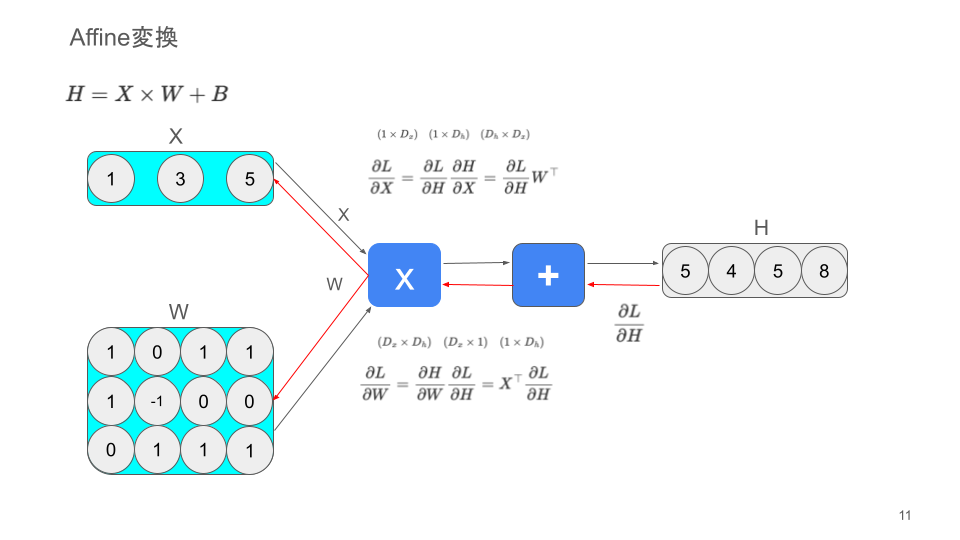
Affine変換における足し算と掛け算の使い分け
| 操作 | 足し算 | 掛け算 |
|---|---|---|
| 目的 | 線形結合(重み付きの総和を計算) | 順伝播:入力と重みのスケーリング(重み付き入力) 逆伝播:勾配伝播(誤差の連鎖的な計算) |
| 数式の文脈 | $z = w^\top x + b$ | 順伝播:$w⋅x$ 逆伝播:$\frac{\partial L}{\partial w} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial w}$ |
| 使用箇所 | 順伝播(入力から出力を計算する過程) | 順伝播:(重み付き入力の計算) 逆伝播:(勾配を計算して重みを更新する過程) |
| 役割 | ネットワークの各ニューロン間の結合値を決定 | 順伝播:入力信号の重要性を反映 逆伝播:誤差を伝播して最適化を行う |
シグモイド関数の逆伝播
シグモイド関数の数式
$$h = \sigma(x) = \frac{1}{1 + e^{-x}}$$
シグモイド関数の微分式
$$\frac{\partial h}{\partial x} = h{(1 – h)}$$

シグモイド関数の微分式の詳細
商の微分方式により
$$\left(\frac{1}{1 + e^{-x}}\right)’ =
\frac{\frac{\partial}{\partial x}(1) \cdot (1 + e^{-x}) – 1 \cdot \frac{\partial}{\partial x}(1 + e^{-x})}{(1 + e^{-x})^2}$$
- $u=1$ のため、$u’ = 0$。
- $v = 1 + e^{-x}$ のため、$v’ = -e^{-x}$(指数関数の微分を適用)。
代入すると
$$\frac{\partial h}{\partial x} =
\frac{0 \cdot (1 + e^{-x}) – 1 \cdot (-e^{-x})}{(1 + e^{-x})^2} =
\frac{e^{-x}}{(1 + e^{-x})^2}$$
分母を分解して簡略化
次に、シグモイド関数 $h = \frac{1}{1 + e^{-x}}$ の性質を使って式を簡略化します。
$$1 – h = 1 – \frac{1}{1 + e^{-x}} = \frac{1 + e^{-x} – 1}{1 + e^{-x}} = \frac{e^{-x}}{1 + e^{-x}}$$
ここで $h$ と $1 – h$ を用いると、微分結果を次のように書き換えることができます。
$$\frac{\partial h}{\partial x} = \frac{e^{-x}}{(1 + e^{-x})^2} = \frac{1}{1 + e^{-x}} \cdot \frac{e^{-x}}{1 + e^{-x}} = h{(1 – h)}$$
$$\frac{\partial h}{\partial x} = h{(1 – h)}$$
tanhの逆伝播
tanhの数式
$$h = \tanh(x) = \frac{e^x – e^{-x}}{e^x + e^{-x}}$$
tanhの微分式
$$\frac{\partial h}{\partial x} = 1 – {h}^2$$

tanhの微分式の詳細
商の微分方式により
$$\frac{\partial h}{\partial x} = \frac{(e^x + e^{-x})(e^x + e^{-x}) – (e^x – e^{-x})(e^x – e^{-x})}{(e^x + e^{-x})^2}$$
$$= 1 – \left(\frac{e^x – e^{-x}}{e^x + e^{-x}}\right)^2$$
$$\frac{\partial h}{\partial x} = 1 – {h}^2$$
ReLU関数の逆関数
$$h = \text{ReLU}(x) =
\begin{cases}
x & (x > 0) \\
0 & (x \leq 0)
\end{cases}$$
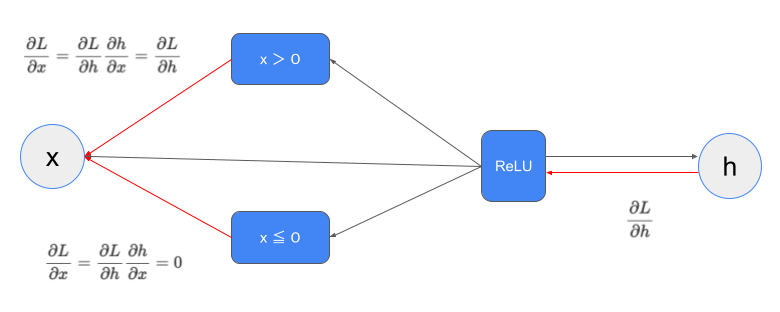
softmax関数の逆関数
softmax関数の数式
$$h_k = \text{softmax}(x_k) = \frac{e^{x_k}}{\sum_j e^{x_j}}$$
- $xk$ は入力値(スコア)。
- $h_k$ はクラス $k$ の確率。
- 分母は全ての入力値の指数関数の和で、確率の総和が 1 になるように正規化しています。
softmax関数の微分式
$$\frac{\partial h_k}{\partial x_l} =
\begin{cases}
h_k (1 – h_k) & (k = l \text{ のとき}) \\
-h_k h_l & (k \neq l \text{ のとき})
\end{cases}$$
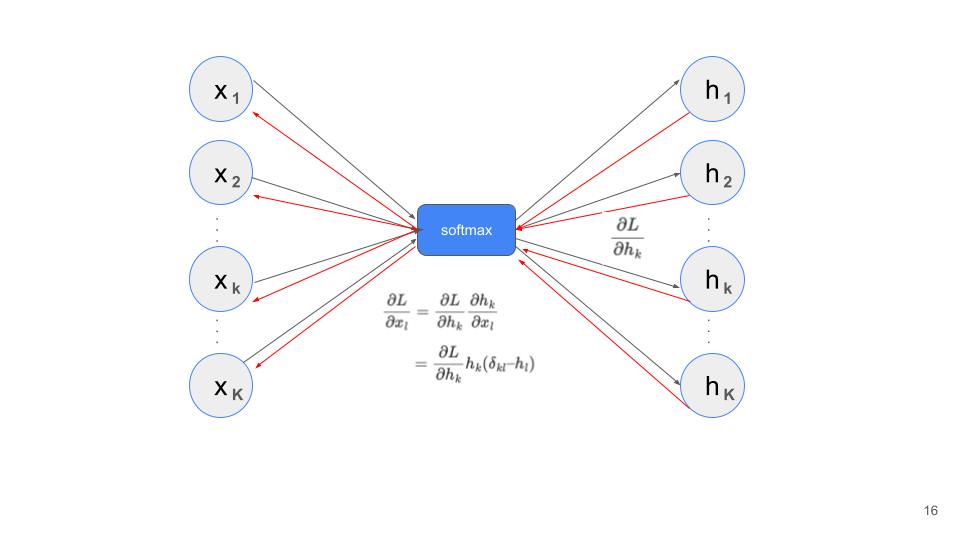
softmaxの微分式の詳細
softmax関数の微分には、同じインデックスの場合 ($k = l$) と 異なるインデックスの場合 ($k≠l$) の2つのケースを考える必要があります。
- $k = l$ の場合
$$\frac{\partial h_k}{\partial x_k} = \frac{\partial}{\partial x_k} \left( \frac{e^{x_k}}{S} \right)$$
商の微分法則を適用
$$\frac{\partial h_k}{\partial x_k} = \frac{\frac{\partial e^{x_k}}{\partial x_k} \cdot S – e^{x_k} \cdot \frac{\partial S}{\partial x_k}}{S^2}$$
- $\frac{\partial e^{x_k}}{\partial x_k} = e^{x_k}$
- $S = \sum_j e^{x_j}$ のため、$\frac{\partial S}{\partial x_k} = e^{x_k}$
これらを代入すると
$$\frac{\partial h_k}{\partial x_k} = \frac{e^{x_k} \cdot S – e^{x_k} \cdot e^{x_k}}{S^2}$$
$$\frac{\partial h_k}{\partial x_k} = \frac{e^{x_k}(S – e^{x_k})}{S^2}$$
さらに、$h_k = \frac{e^{x_k}}{S}$ を代入して整理すると
$$\frac{\partial h_k}{\partial x_k} = h_k \cdot (1 – h_k)$$
- $k≠l$の場合
この場合、微分対象は $h_k$ に対して異なるインデックス $x_l$ の微分を求めます。
$$\frac{\partial h_k}{\partial x_l} = \frac{\partial}{\partial x_l} \left( \frac{e^{x_k}}{S} \right)$$
$$\frac{\partial h_k}{\partial x_l} = \frac{\frac{\partial e^{x_k}}{\partial x_l} \cdot S – e^{x_k} \cdot \frac{\partial S}{\partial x_l}}{S^2}$$
- $\frac{\partial e^{x_k}}{\partial x_l} = 0$ (指数関数の入力が異なるため)。
- $\frac{\partial S}{\partial x_l} = e^{x_l}$ (分母の総和に含まれるため)。
これらを代入すると
$$\frac{\partial h_k}{\partial x_l} = \frac{0 \cdot S – e^{x_k} \cdot e^{x_l}}{S^2}$$
$$\frac{\partial h_k}{\partial x_l} = -\frac{e^{x_k} e^{x_l}}{S^2}$$
$h_k = \frac{e^{x_k}}{S}$ , $h_l = \frac{e^{x_l}}{S}$ を代入して整理すると
$$\frac{\partial h_k}{\partial x_l} = -h_k \cdot h_l$$
微分結果
$$\frac{\partial h_k}{\partial x_l} =
\begin{cases}
h_k (1 – h_k) & (k = l \text{ のとき}) \\
-h_k h_l & (k \neq l \text{ のとき})
\end{cases}$$
$$\frac{\partial h_k}{\partial x_l} = h_k (\delta_{kl} – h_l)$$
$$\text{ただし } \delta_{kl} =
\begin{cases}
1 & (k = l \text{ のとき}) \\
0 & (k \neq l \text{ のとき})
\end{cases}$$
Softmax With CrossEntropyの逆伝播
softmaxの数式
$$h_k = \text{softmax}(x_k) = \frac{e^{x_k}}{\sum_j e^{x_j}}$$
クロスエントロピーの数式
$$L = CE(t, y) = -\sum_k t_k \log y_k$$
Softmax With CrossEntropyの微分
$$\frac{\partial L}{\partial x_l} = y_l – t_l$$
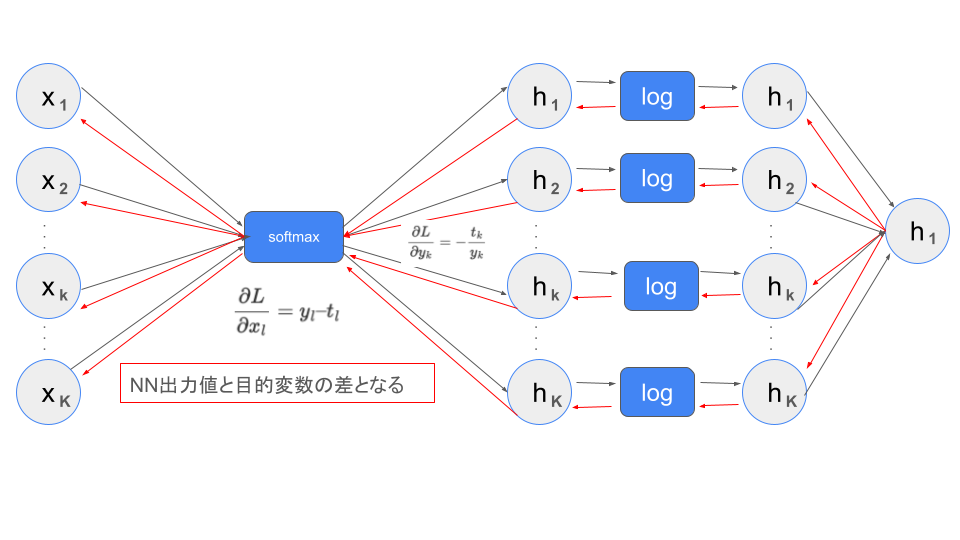
クロスエントロピーの微分
クロスエントロピーの数式
$$L = CE(t, y) = -\sum_k t_k \log y_k$$
- $tk$ は目標値(ターゲットラベル、通常は 0 または 1 )。
- $y_k$ はモデルの出力(通常は softmax 関数の出力で、 $0 \leq y_k \leq 1$ を満たす)。
- $k$ はクラスのインデックスを表します。
クロスエントロピーの微分式
$$\frac{\partial L}{\partial y_k} = -\frac{t_k}{y_k}$$
クロスエントロピーの微分式の詳細
損失関数 $L$ を、softmax 出力 $y_k$ に関して微分します。
$$\frac{\partial L}{\partial y_k} = \frac{\partial}{\partial y_k} \left( -\sum_k t_k \log y_k \right)$$
クロスエントロピー損失はクラスごとに独立しているため、サミングインデックス $k$ の中から1つを取り出します。つまり、 $t_k \log y_k$ の微分を考えれば十分です。
$$\frac{\partial L}{\partial y_k} = -\frac{\partial}{\partial y_k} \left( t_k \log y_k \right)$$
ここで、 $\log y_k$ の微分は次のようになります。
$$\frac{\partial \log y_k}{\partial y_k} = \frac{1}{y_k}$$
したがって、
$$\frac{\partial L}{\partial y_k} = -t_k \cdot \frac{1}{y_k}$$
つまり、
$$\frac{\partial L}{\partial y_k} = -\frac{t_k}{y_k}$$
Softmax With CrossEntropyの微分
クロスエントロピーの微分
$$\frac{\partial L}{\partial y_k} = -\frac{t_k}{y_k}$$
softmaxの微分
$k = l$の場合
$$\frac{\partial y_k}{\partial x_l} = y_k (1 – y_k)$$
$k≠l$ の場合
$$\frac{\partial y_k}{\partial x_l} = -y_k y_l$$
損失関数の計算
$$\frac{\partial L}{\partial x_l} = \sum_k \frac{\partial L}{\partial y_k} \cdot \frac{\partial y_k}{\partial x_l}$$
- k = l の項
$$\frac{\partial L}{\partial y_k} \cdot \frac{\partial y_k}{\partial x_l} = \left( -\frac{t_k}{y_k} \right) \cdot \left( y_k (1 – y_k) \right) = -t_k (1 – y_k)$$ - $k≠l$ の項
$$\frac{\partial L}{\partial y_k} \cdot \frac{\partial y_k}{\partial x_l} = \left( -\frac{t_k}{y_k} \right) \cdot \left( -y_k y_l \right) = t_k y_l$$
結果の合成
全ての $k$ の項を合計します。
$$\frac{\partial L}{\partial x_l} = -t_l (1 – y_l) + \sum_{k \neq l} t_k y_l$$
ここで、クロスエントロピーのターゲットラベル $t_k$ の性質( $\sum_k t_k = 1$ )を用いると
$$\sum_k t_k y_l = y_l \sum_k t_k = y_l$$
したがって、微分は次のように簡略化されます。
$$\frac{\partial L}{\partial x_l} = y_l – t_l$$
Softmax With CrossEntropyの実装(分類タスク)
import torch
import torch.nn as nn
import torch.optim as optim
# データ作成 (分類タスク用)
x_class = torch.tensor([[1.0, 2.0], [2.0, 1.5], [1.5, 1.5], [2.0, 2.0]])
y_class = torch.tensor([0, 1, 0, 1]) # 2クラス分類
# モデル構築
class ClassificationModel(nn.Module):
def __init__(self, input_size, output_size):
super(ClassificationModel, self).__init__()
self.fc = nn.Linear(input_size, output_size)
def forward(self, x):
return self.fc(x)
model_class = ClassificationModel(input_size=2, output_size=2)
# 損失関数と最適化手法
criterion_class = nn.CrossEntropyLoss()
optimizer_class = optim.SGD(model_class.parameters(), lr=0.01)
# 学習ループ
for epoch in range(100):
optimizer_class.zero_grad()
outputs = model_class(x_class)
loss = criterion_class(outputs, y_class)
loss.backward()
optimizer_class.step()
if epoch % 10 == 0:
print(f'Epoch [{epoch}], Loss: {loss.item()}')
print("分類モデルの学習完了")Epoch [70], Loss: 0.7429901957511902
Epoch [80], Loss: 0.7369784116744995
Epoch [90], Loss: 0.7315465211868286
分類モデルの学習完了このコードは、PyTorchを使用してシンプルな分類モデルを構築し、誤差逆伝播と勾配降下法を使用してモデルを学習する例を示しています。学習ループ内で順伝播、損失計算、誤差逆伝播、勾配降下法を実行し、モデルのパラメータを更新しています。
Linear With MSE の逆伝播
恒等関数の数式
$$y = \text{Linear}(x) = x$$
MSEの数式
$$L = \text{MSE}(t, y) = \frac{1}{2}(y – t)^2$$
Linear With MSEの微分
$$\frac{\partial L}{\partial x} = y – t$$

MSEの微分
$$\frac{\partial L}{\partial x} = y – t$$
MSEの微分の詳細
$$\frac{\partial L}{\partial y} = \frac{\partial}{\partial y} \left( \frac{1}{2}(y – t)^2 \right)$$
連鎖律を適用
平方項の微分を考えると
$$\frac{\partial}{\partial y} \left( (y – t)^2 \right) = 2(y – t) \cdot \frac{\partial}{\partial y}(y – t)$$
ここで、$\frac{\partial}{\partial y}(y – t) = 1$ なので
$$\frac{\partial}{\partial y}\left((y – t)^2\right) = 2(y – t)$$
定数 $\frac{1}{2}$ を反映
損失関数全体を微分すると
$$\frac{\partial L}{\partial y} = \frac{1}{2} \cdot 2(y – t) \\$$
$$= y – t$$
Linear With MSEの微分の詳細
$$y = \text{Linear}(x) = x \\$$
$$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial x} \\$$
$$=(y – t) \cdot 1 \\$$
$$= y – t$$
Linear With MSE(回帰タスク)
# データ作成 (回帰タスク用)
x_reg = torch.tensor([[1.0], [2.0], [3.0], [4.0]])
y_reg = torch.tensor([[2.0], [4.0], [6.0], [8.0]])
# モデル構築
class RegressionModel(nn.Module):
def __init__(self, input_size, output_size):
super(RegressionModel, self).__init__()
self.fc = nn.Linear(input_size, output_size)
def forward(self, x):
return self.fc(x)
model_reg = RegressionModel(input_size=1, output_size=1)
# 損失関数と最適化手法
criterion_reg = nn.MSELoss()
optimizer_reg = optim.SGD(model_reg.parameters(), lr=0.01)
# 学習ループ
for epoch in range(100):
optimizer_reg.zero_grad()
outputs = model_reg(x_reg)
loss = criterion_reg(outputs, y_reg)
loss.backward()
optimizer_reg.step()
if epoch % 10 == 0:
print(f'Epoch [{epoch}], Loss: {loss.item()}')
print("回帰モデルの学習完了")Epoch [70], Loss: 0.16236446797847748
Epoch [80], Loss: 0.15291401743888855
Epoch [90], Loss: 0.1440136730670929
回帰モデルの学習完了このコードは、PyTorchを使用してシンプルな回帰モデルを構築し、誤差逆伝播と勾配降下法を使用してモデルを学習する例を示しています。学習ループ内で順伝播、損失計算、誤差逆伝播、勾配降下法を実行し、モデルのパラメータを更新しています。
損失関数と微分式
| 出力ユニット | 用途 | 損失関数の式 | 損失関数の微分 |
|---|---|---|---|
| 線形ユニット | 回帰に使われるコスト関数 | $L = \frac{1}{2}(t – y)^2$ | $\frac{\partial L}{\partial y} = y – t$ |
| シグモイドユニット | 2値のクラス分類に使われるコスト関数 | $L = -t \log y – (1 – t)$ $\log(1 – y)$ | $\frac{\partial L}{\partial y} = {y(1 – y)}$ |
| ソフトマックスユニット | 多項クラス分類に使われるコスト関数 | $L = – \sum_{i=0}^n t_i \log y_i$ | $\frac{\partial L}{\partial y_i} = y_i – t_i$ |
| Softmax + CrossEntropy | 多項クラス分類に使われる効率的な計算 | $L= \frac{e^{x_k}}{\sum_j e^{x_j}}$ $L = -\sum_k t_k \log y_k$ |
$\frac{\partial L}{\partial x_l} = y_l – t_l$ |
| Linear + MSE | 回帰に使われる効率的な計算 | $y = x$ $L = \frac{1}{2}(y – t)^2$ |
$\frac{\partial L}{\partial x} = y – t$ |
学習の振り返りと次回予告
今回の学びでは、ニューラルネットワークにおける各出力ユニット(線形、シグモイド、ソフトマックス)の損失関数と微分の詳細を深く理解することができる内容であったかと思います。特に、Softmax with CrossEntropyの効率的な計算方法やLinear with MSEの単純かつ効果的な回帰タスクへの応用が重要でした。また、これらの数学的な基盤は、逆伝播やモデル最適化に直結する基本技術です。次回は、今回学んだ損失関数と微分を活用し、回帰タスクや分類タスクに特化したモデルをPyTorchで構築し、その性能を実データで評価する予定です。
今回の学習の応用としてのモデル実装
回帰モデル
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# データセットのロード
data = pd.read_csv('https://raw.githubusercontent.com/ageron/handson-ml2/master/datasets/housing/housing.csv')
# 特徴量とターゲットの選択
X = data[['total_rooms']].values # シンプルな例としてtotal_roomsを使用
y = data['median_house_value'].values
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# データの標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# データをPyTorchのテンソルに変換
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32).view(-1, 1)
y_test = torch.tensor(y_test, dtype=torch.float32).view(-1, 1)# モデル構築
class RegressionModel(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(RegressionModel, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, output_size)
# He初期化を適用
nn.init.kaiming_uniform_(self.fc1.weight, nonlinearity='relu')
nn.init.kaiming_uniform_(self.fc2.weight, nonlinearity='relu')
nn.init.zeros_(self.fc1.bias)
nn.init.zeros_(self.fc2.bias)
def forward(self, x):
out = self.fc1(x)
out = self.relu(out)
out = self.fc2(out)
return out
model_reg = RegressionModel(input_size=1, hidden_size=10, output_size=1)
# 損失関数と最適化手法
criterion_reg = nn.MSELoss()
optimizer_reg = optim.Adam(model_reg.parameters(), lr=0.01)
# 学習ループ
num_epochs = 100
train_losses = []
test_losses = []
for epoch in range(num_epochs):
model_reg.train()
optimizer_reg.zero_grad()
outputs = model_reg(X_train)
loss = criterion_reg(outputs, y_train)
loss.backward()
optimizer_reg.step()
train_losses.append(loss.item())
model_reg.eval()
with torch.no_grad():
test_outputs = model_reg(X_test)
test_loss = criterion_reg(test_outputs, y_test)
test_losses.append(test_loss.item())
if epoch % 10 == 0:
print(f'Epoch [{epoch}/{num_epochs}], Train Loss: {loss.item()}, Test Loss: {test_loss.item()}')
print("回帰モデルの学習完了")Epoch [70/100], Train Loss: 56293511168.0, Test Loss: 55330500608.0
Epoch [80/100], Train Loss: 56292372480.0, Test Loss: 55329353728.0
Epoch [90/100], Train Loss: 56291012608.0, Test Loss: 55327989760.0
回帰モデルの学習完了分類モデル
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# データセットのロード
data = pd.read_csv('https://raw.githubusercontent.com/datasciencedojo/datasets/master/titanic.csv')
# 特徴量とターゲットの選択
X = data[['Pclass', 'Age', 'SibSp', 'Parch', 'Fare']].fillna(0).values # シンプルな例としていくつかの特徴量を使用
y = data['Survived'].values
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# データの標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# データをPyTorchのテンソルに変換
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.long)
y_test = torch.tensor(y_test, dtype=torch.long)# モデル構築
class ClassificationModel(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(ClassificationModel, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, output_size)
# He初期化を適用
nn.init.kaiming_uniform_(self.fc1.weight, nonlinearity='relu')
nn.init.kaiming_uniform_(self.fc2.weight, nonlinearity='relu')
nn.init.zeros_(self.fc1.bias)
nn.init.zeros_(self.fc2.bias)
def forward(self, x):
out = self.fc1(x)
out = self.relu(out)
out = self.fc2(out)
return out
model_class = ClassificationModel(input_size=5, hidden_size=10, output_size=2)
# 損失関数と最適化手法
criterion_class = nn.CrossEntropyLoss()
optimizer_class = optim.Adam(model_class.parameters(), lr=0.01)
# 学習ループ
num_epochs = 100
train_losses = []
test_losses = []
train_accuracies = []
test_accuracies = []
for epoch in range(num_epochs):
model_class.train()
optimizer_class.zero_grad()
outputs = model_class(X_train)
loss = criterion_class(outputs, y_train)
loss.backward()
optimizer_class.step()
train_losses.append(loss.item())
_, predicted = torch.max(outputs.data, 1)
train_accuracy = (predicted == y_train).sum().item() / y_train.size(0)
train_accuracies.append(train_accuracy)
model_class.eval()
with torch.no_grad():
test_outputs = model_class(X_test)
test_loss = criterion_class(test_outputs, y_test)
test_losses.append(test_loss.item())
_, test_predicted = torch.max(test_outputs.data, 1)
test_accuracy = (test_predicted == y_test).sum().item() / y_test.size(0)
test_accuracies.append(test_accuracy)
if epoch % 10 == 0:
print(f'Epoch [{epoch}/{num_epochs}], Train Loss: {loss.item()}, Test Loss: {test_loss.item()}, Train Accuracy: {train_accuracy}, Test Accuracy: {test_accuracy}')
print("分類モデルの学習完了")
# 学習曲線のプロット
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(train_losses, label='Train Loss')
plt.plot(test_losses, label='Test Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training and Testing Loss')
plt.legend()
plt.grid(True)
plt.subplot(1, 2, 2)
plt.plot(train_accuracies, label='Train Accuracy')
plt.plot(test_accuracies, label='Test Accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title('Training and Testing Accuracy')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()Epoch [70/100], Train Loss: 0.5666111707687378, Test Loss: 0.5306118130683899, Train Accuracy: 0.7106741573033708, Test Accuracy: 0.7541899441340782
Epoch [80/100], Train Loss: 0.5637770891189575, Test Loss: 0.5300860404968262, Train Accuracy: 0.7191011235955056, Test Accuracy: 0.7653631284916201
Epoch [90/100], Train Loss: 0.5619109272956848, Test Loss: 0.529148280620575, Train Accuracy: 0.7162921348314607, Test Accuracy: 0.7653631284916201
分類モデルの学習完了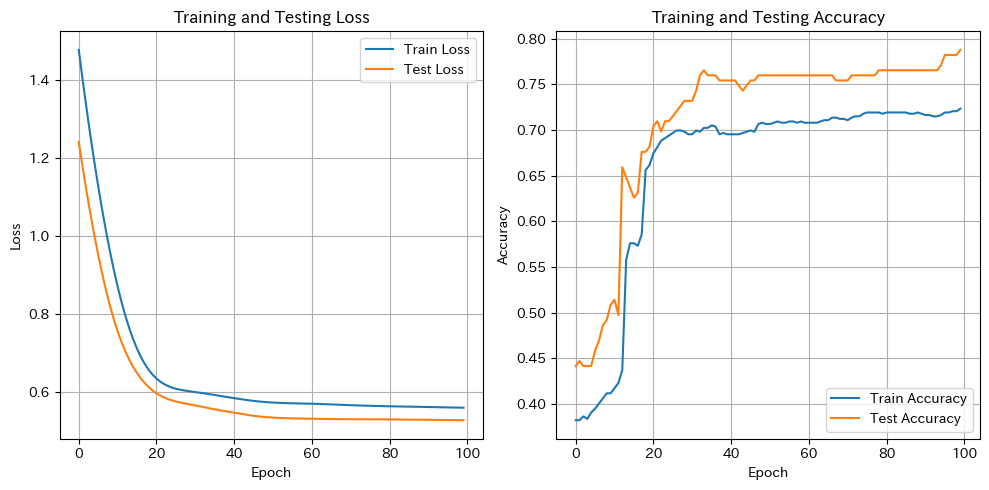



コメント