【第7回】教師あり学習の基礎と代表的なアルゴリズム（後編）

機械学習
2024.11.02

目的

このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用できる力を養うことが目的です。この過程で、実践的な演習やプロジェクトを通じて、手を動かしながら学ぶ姿勢を大切にしていきます。

第7回の目標

機械学習は、大きく分けて教師あり学習と教師なし学習の二つのカテゴリーに分類されます。今回のテーマである教師あり学習は、入力データとそれに対応する正解（ラベル）が与えられた状態でモデルを学習させる手法です。これにより、新たなデータに対して正確な予測や分類を行うことが可能となります。

  • 教師あり学習の基本的な概念と重要性を理解する。
  • 代表的な教師あり学習アルゴリズムの理論と実装方法を学ぶ。
  • 各アルゴリズムの特徴や適用例を把握し、適切な場面で選択・活用できるようになる。

サポートベクターマシン (SVM)

サポートベクターマシンは、分類や回帰に対応する機械学習の代表的な手法で、特に「最大マージン分類」を用いて汎化性能を高めたモデルを構築するアルゴリズムです。「カーネル関数」と「マージン最大化」を組み合わせたことで、特に非線形データの分類に強いアルゴリズムです。

カーネル関数とは？：

カーネル関数は、データを高次元の空間に「写像」するための方法です。これにより、元々は線形分離が難しい複雑なデータでも、新しい高次元の空間で線形に分割できるようになります。例えば、円や曲線で分ける必要があるデータも、カーネル関数を使うことで平面で分けられるようになるのです。

AI研究所

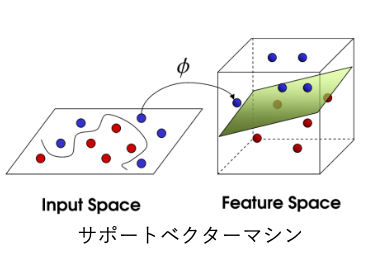
マージン最大化：

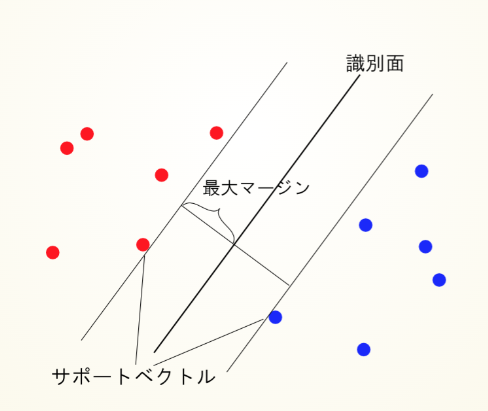
SVM（サポートベクターマシン）は、異なるクラスを分ける「境界線」（超平面）と、その境界に最も近いデータポイント（サポートベクター）との距離、つまり「マージン」を最大化するように設計されたアルゴリズムです。このマージンを最大化することで、分類の安定性と汎化性能が向上し、未知のデータにも精度高く対応できるようになります。

SVMは、2つのクラスを分離する際、クラス間の「境界」（超平面）を見つけ出し、サポートベクターとのマージンが最も広くなるように調整します。これにより、クラスの境界が明確になり、未知のデータに対しても安定した分類が可能です。この特性により、SVMは新しいデータに対する予測性能が高く、複雑なパターンを持つデータにも対応できるモデルとして多くの分野で利用されています。


https://nineties.github.io/prml-seminar/12.html#/7

ハードマージンとソフトマージン

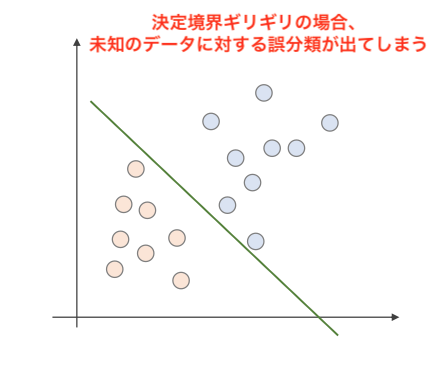
SVMはデータを分離する超平面を探し、最大のマージンを確保します。しかし、決定境界がギリギリだと、未知のデータに対する誤分類が出てしまい、すべてのデータが完全に線形分離できるとは限らないため、以下の2つのアプローチを用います。

ハードマージン SVM

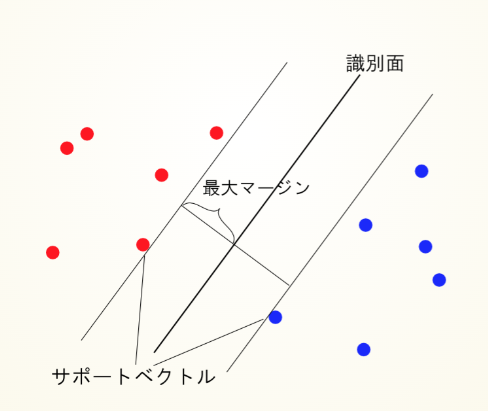
ハードマージンSVMでは、データが完全に線形分離可能であり、マージンを最大化することで最適な識別器（超平面）を見つけます。ここでは、ラグランジュ未定乗数法を使って、このマージン最大化問題を解いていきます。

  1. マージンの定義と識別器の条件：

まず、データセットには $m$ 個のデータポイントがあり、各データポイント $x_i$ は $n$ 次元のベクトルで、ラベル $y_i \in \{1, -1\}$ が付与されています。ハードマージンSVMでは、以下の超平面を定義します。

$$w⋅x+b=0$$

ここで、$w$ は法線ベクトル、$b$ はバイアス項です。SVMは、この超平面と各クラスの最も近いデータ点（サポートベクトル）との距離（マージン）を最大化します。

サポートベクトルとの距離を考える際、超平面の法線ベクトル $w$ は定数倍してもマージンの距離が変わらないため、スケーリング制約として次を設定します。

$$∥w∥=1$$

この制約のもとで、データのラベルに応じて以下の識別条件が成り立ちます。

$$y_i (w \cdot x_i + b) \geq 1, \quad \forall i$$

  • $\forall i$ = すべての $i$ に対して
  • $w$ は法線ベクトル
  • $b$ はバイアス項

この条件により、データ点が超平面から1以上の距離を持つことが保証されます。

2. マージン最大化のための最適化問題：

マージンの最大化は、$\frac{1}{\|w\|}$ の最大化と等価です。これを最小化問題に変換すると、次のようになります。

$$\text{min} \quad \frac{1}{2} \|w\|^2$$

$$\text{s.t. } \quad y_i (w \cdot x_i + b) \geq 1, \, \forall i$$

$s.t.$ = $subject to$（数理最適化問題の記述の際に用いる）

https://nineties.github.io/prml-seminar/12.html#/7
ラグランジュ未定乗数法の適用

ラグランジュ未定乗数法を用いることで、制約条件を満たしつつ最適化問題を解きます。制約条件を考慮して、次のラグランジュ関数 $L$ を定義します。

ラグランジュ関数：

$$L(w, b, \alpha) = \frac{1}{2} \|w\|^2 – \sum_{i=1}^{m} \alpha_i \left( y_i (w \cdot x_i + b) – 1 \right)$$

ここで、$\alpha_i$ はラグランジュ乗数です。

この関数 $L$ を $w$ と $b$ で偏微分し、それらの勾配が0になる条件から最適解を求めます。

w に関する微分：

$$\frac{\partial L}{\partial w} = w – \sum_{i=1}^{m} \alpha_i y_i x_i$$

この微分がゼロになる条件：

$$\frac{\partial L}{\partial w} = 0 \Rightarrow w – \sum_{i=1}^{m} \alpha_i y_i x_i = 0$$

したがって、

$$w = \sum_{i=1}^{m} \alpha_i y_i x_i \quad \cdots (1)$$

b に関する微分：

$$\frac{\partial L}{\partial b} = -\sum_{i=1}^{m} \alpha_i y_i$$

この微分がゼロになる条件：

$$\frac{\partial L}{\partial b} = 0 \Rightarrow -\sum_{i=1}^{m} \alpha_i y_i = 0$$

したがって、

$$\sum_{i=1}^{m} \alpha_i y_i = 0 \quad \cdots (2)$$

$w$ の最適解：

$$w = \sum_{i=1}^{m} \alpha_i y_i x_i$$

これにより、最適な重み $w$ とバイアス $b$ が得られることが確認できます。最適化の条件は、ラグランジュ乗数法を用いて導出されるサポートベクターマシンの解を示しています。

3. 最適化問題の表現：

得られた $w$ をラグランジュ関数に代入し、最適化問題を導きます。

$$\max \sum_{i=1}^{m} \alpha_i – \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j (x_i \cdot x_j)$$

制約条件：

$$\text{s.t.} \quad \sum_{i=1}^{m} \alpha_i y_i = 0, \quad \alpha_i \geq 0$$

ソフトマージンSVM

ソフトマージンSVMは、データが完全に線形分離できない場合に適用します。制約に誤差を許容するため、スラック変数 $ξ_i$​ を導入します。

  1. スラック変数を用いた最適化問題：

$$\min_\quad \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{m} \xi_i$$

$$\text{s.t. } \quad y_i (w \cdot x_i + b) \geq 1 – \xi_i, \quad \xi_i \geq 0, \, \forall i$$

  • $C$ は誤差に対するペナルティ項であり、誤分類の度合いを調整します。

2. ラグランジュ未定乗数法の適用：

ソフトマージンSVMの最適化も、ラグランジュ未定乗数法を用いて解きます。

$$L(w, b, \alpha, \xi) = \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{m} \xi_i – \sum_{i=1}^{m} \alpha_i \left( y_i (w \cdot x_i + b) – 1 + \xi_i \right) – \sum_{i=1}^{m} \mu_i \xi_i$$

ここで、$\alpha_i$ と $\mu_i$ はそれぞれの制約条件に対するラグランジュ乗数です。

3. 最適化問題の表現：

まず、ハードマージンと同様にラグランジュ関数 $L$ を $w$ と$b$ で偏微分し、勾配が0になる条件を求めます。

$$(w)\cdots \frac{\partial L}{\partial w} = 0 \Rightarrow w – \sum_{i=1}^{m} \alpha_i y_i x_i = 0$$
$$w = \sum_{i=1}^{m} \alpha_i y_i x_i \quad$$

$$(b)\cdots \frac{\partial L}{\partial b} = 0 \Rightarrow -\sum_{i=1}^{m} \alpha_i y_i = 0$$
$$\sum_{i=1}^{m} \alpha_i y_i = 0 \quad$$

4. ξi​ に関する最適化条件：

最後に、ラグランジュ関数 $L$ を $ξ_i$​ で微分し、勾配が0になる条件を求めます。

$$\frac{\partial L}{\partial \xi_i} = C – \alpha_i – \mu_i = 0$$

したがって、

$$\alpha_i = C – \mu_i$$

ここで、$α_i≥0$ および $μ_i≥0$ であることから、

$$0 \leq \alpha_i \leq C$$

という制約が成り立ちます。

$α_i$ はラグランジュ乗数、$C$ はソフトマージンの制御パラメータで、データの誤分類に対するペナルティを調整します。

最適化条件をまとめると、次のようになります。

  1. $w = \sum_{i=1}^{m} \alpha_i y_i x_i \quad$
  2. $\sum_{i=1}^{m} \alpha_i y_i = 0 \quad$
  3. $0 \leq \alpha_i \leq C$

これらの条件のもとで、ラグランジュ未定乗数法によりソフトマージンSVMの最適化が行われ、最適な識別器を構築することができます。

カーネル関数（カーネルトリック）

カーネルトリックは、非線形分離が難しいデータを高次元空間にマッピングし、そこで線形分離を可能にする手法です。SVMにカーネルトリックを適用することで、非線形データも高次元空間での線形分離が可能となります。この方法では、データを高次元の特徴ベクトル $\phi(x)$ にマッピングして分離しますが、直接マッピングすると計算量が増大するため、カーネル関数 $K(x^{(i)}, x^{(j)})$ を用いて内積計算を効率化します。これにより、明示的に高次元空間を計算せずに複雑なデータ構造を扱えるのです。

RBFカーネルの例

$$\max \sum_{i=1}^{m} \alpha_i – \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j (x_i \cdot x_j)$$

  • $α_i$​ はラグランジュ乗数
  • $y^{(i)}$ はラベル
  • $\langle x^{(i)}, x^{(j)}⟩$ はデータの内積

カーネル関数 $K(x^{(i)}, x^{(j)})$ は、次のような写像関数 $\phi(x)$ の内積として表されます。

高次元へのマッピングとカーネル関数：非線形な境界が必要な場合、入力データ $x$ を高次元空間での特徴ベクトル $\phi(x)$ にマッピングします。内積の代わりに、カーネル関数 $K(x^{(i)}, x^{(j)})$ を使って、次のように置き換えます

$$K(x^{(i)}, x^{(j)}) = \phi(x^{(i)}) \cdot \phi(x^{(j)})$$

カーネルを使った最適化：カーネルトリックを適用したSVMの最適化の式は以下のようになります。

$$\max \sum_{i=1}^{n} \alpha_i – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y^{(i)} y^{(j)} K(x^{(i)}, x^{(j)})$$

$subject to$

$$\sum_{i=1}^{n} \alpha_i y^{(i)} = 0, \quad 0 \leq \alpha_i \leq C$$

カーネルによる判別関数：学習が完了した後の分類関数は、サポートベクトルのみを使って次のように書けます。

$$f(x) = \sum_{i=1}^{n} \alpha_i y^{(i)} K(x^{(i)}, x) + b$$

ここで、カーネル K(x^{(i)}, x)は、入力データとサポートベクトルの内積を表します。カーネルによって、非線形の境界を効率的に学習し、計算コストを抑えながら高次元空間での分類を実現しています。

カーネル関数の例

SVMにおいて選択するカーネル関数の種類により、適用できるデータやモデルの性能が変わります。以下に代表的なカーネル関数をいくつか紹介します。

  • 線形カーネル：線形分離可能な問題に適しています。

$$K(x^{(i)}, x^{(j)}) = x^{(i)} \cdot x^{(j)}$$

  • 多項式カーネル：次数を指定することで多項式の分離面を生成します。

$$K(x^{(i)}, x^{(j)}) = (x^{(i)} \cdot x^{(j)} + c)^d$$

$c$ は定数、$d$ は次数

  • RBF（ガウス）カーネル： 非線形分布に対して柔軟な境界を提供するため、最も一般的に使用されます。

$$K(x^{(i)}, x^{(j)}) = \exp\left(-\frac{\|x^{(i)} – x^{(j)}\|^2}{2\sigma^2}\right)$$

  • シグモイドカーネル：ニューラルネットワークに類似しており、非線形の特徴を捉えることができます。

$$K(x^{(i)}, x^{(j)}) = \tanh(\alpha x^{(i)} \cdot x^{(j)} + c)$$

サポートベクターマシンの実装

SVCはカーネル関数を使って非線形分離が可能な一方で、LinearSVCは線形カーネル専用であり、大規模データセットに対して計算効率が高いです。

項目SVC (Support Vector Classification)LinearSVC
基本的な違いカーネル関数を使用し、非線形の決定境界を学習できる。デフォルトでRBFカーネルが使用される。線形カーネルのみを使用するため、線形分離可能なデータに適している。
柔軟性非線形データに対応可能で、さまざまなカーネルを指定して柔軟なモデルを構築できる。線形モデルに限定されるが、大規模データに対して効率的。
計算効率非線形モデルのため、大規模データに対しては計算コストが高くなる場合がある。線形モデルのため、特徴量やサンプル数が多い場合でも効率的に学習可能。
ハイパーパラメータkernel パラメータでカーネルの種類を指定可能（例: ‘linear’, ‘rbf’ など）。
C パラメータで誤分類の許容度を制御。		C パラメータで誤分類の許容度を制御。
max_iter で最大反復回数を指定。
dual で双対問題の解法を選択可能。
使用シーン非線形データや複雑な決定境界が必要な場合に適している。
カーネルの変更で多様なデータに対応可能。		線形分離可能なデータや計算効率が求められる場合に適している。
特徴量が多いデータセットに適する。

LinearSVCの実装

Irisデータセットを使用して、LinearSVCで実装を行います。LinearSVC は SVM（サポートベクターマシン）アルゴリズムの一種として位置づけられます。

# 必要なライブラリのインポート
import numpy as np
import pandas as pd
from pandas import DataFrame
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
# データの準備
iris = load_iris()
df = DataFrame(iris["data"], columns=iris.feature_names)
df_target = DataFrame(iris.target, columns=["target"])
df = pd.concat([df, df_target], axis=1)
# 2値分類データの準備
use_data = df[df.target != 2]
use_data = use_data[['petal length (cm)', 'petal width (cm)', 'target']]
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(use_data.iloc[:, :2].values,
                                                    use_data.iloc[:, 2].values,
                                                    test_size=0.4,
                                                    random_state=42)

# LinearSVCの初期化と学習
model = LinearSVC(random_state=42)
model.fit(X_train, y_train)

# モデルの評価
print('正解率(train): {:.3f}'.format(model.score(X_train, y_train)))
print('正解率(test): {:.3f}'.format(model.score(X_test, y_test)))

# モデルの係数と切片
print('係数:', model.coef_)
print('切片:', model.intercept_)
正解率(train): 1.000
正解率(test): 1.000
係数: [[0.56580853 0.8061934 ]]
切片: [-1.97334243]
# 分類平面の描画
x_min, x_max = X_test[:, 0].min() - 1, X_test[:, 0].max() + 1
x = np.linspace(x_min, x_max, 1000)
y = (-model.coef_[0, 0] * x - model.intercept_[0]) / model.coef_[0, 1]

# 決定境界を描画
plt.plot(x, y, 'k--', label='Decision Boundary')

# データ点のプロット
plt.scatter(X_test[y_test == 0, 0], X_test[y_test == 0, 1], c='red', edgecolors='k', label='target = 0 : setosa')
plt.scatter(X_test[y_test == 1, 0], X_test[y_test == 1, 1], c='blue', edgecolors='k', label='target = 1 : versicolor')

# グラフの設定
plt.xlabel('Petal Length (cm)')
plt.ylabel('Petal Width (cm)')
plt.title('Decision Boundary with LinearSVC')
plt.legend()
plt.show()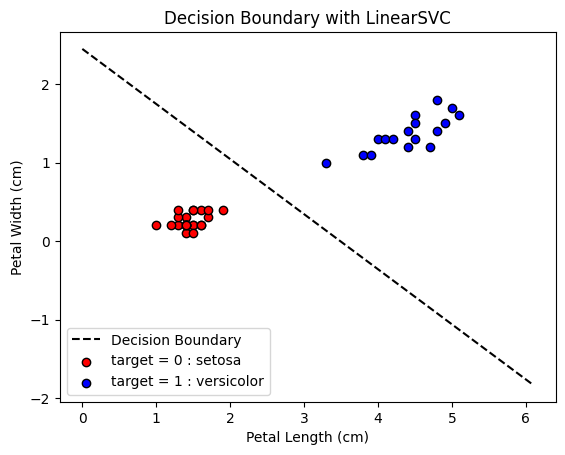

今回の実装では、LinearSVC による学習で高い精度が得られ、テストデータでも 100% の正解率が出たことから、分類が非常に簡単な問題であったことが分かります。この結果は、petal length と petal width の2つの特徴量だけで、「setosa」と「versicolor」の2種類の花を効果的に区別できることを示しています。

描画した分類平面も観察すると、2クラスのデータを分けるラインが中央に引かれており、両クラスのデータ点の距離（マージン）が最大化されているのが視覚的に確認できます。このように、SVMによってクラス間のマージンが最大化されることで、安定した分類モデルが生成されていることが明確に分かります。

サポートベクターマシン(SVC)の実装

SVC を使用し、RBFカーネルを指定します。これにより、非線形の決定境界を学習することができます。

# 必要なライブラリのインポート
import numpy as np
import pandas as pd
from pandas import DataFrame
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC  # LinearSVCではなくSVCをインポート
import matplotlib.pyplot as plt

# データの準備
iris = load_iris()
df = DataFrame(iris["data"], columns=iris.feature_names)
df_target = DataFrame(iris.target, columns=["target"])
df = pd.concat([df, df_target], axis=1)

# 2値分類データの準備 (異なる特徴量を使用)
use_data = df[df.target != 2]
use_data = use_data[['sepal length (cm)', 'sepal width (cm)', 'target']]  # 特徴量を変更

# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(use_data.iloc[:, :2].values,
                                                    use_data.iloc[:, 2].values,
                                                    test_size=0.4,
                                                    random_state=42)

# SVCの初期化と学習
model = SVC(kernel='rbf', random_state=42)  # RBFカーネルを使用
model.fit(X_train, y_train)

# モデルの評価
print('正解率(train): {:.3f}'.format(model.score(X_train, y_train)))
print('正解率(test): {:.3f}'.format(model.score(X_test, y_test)))

# モデルの係数と切片はSVCでは直接取得できないため、決定境界を描画するための方法を変更
# 分類平面の描画
x_min, x_max = X_test[:, 0].min() - 1, X_test[:, 0].max() + 1
y_min, y_max = X_test[:, 1].min() - 1, X_test[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 決定境界を描画
plt.contourf(xx, yy, Z, alpha=0.3)

# データ点のプロット
plt.scatter(X_test[y_test == 0, 0], X_test[y_test == 0, 1], c='red', edgecolors='k', label='target = 0 : setosa')
plt.scatter(X_test[y_test == 1, 0], X_test[y_test == 1, 1], c='blue', edgecolors='k', label='target = 1 : versicolor')

# グラフの設定
plt.xlabel('Sepal Length (cm)')
plt.ylabel('Sepal Width (cm)')
plt.title('Decision Boundary with SVC (RBF Kernel)')
plt.legend()
plt.show()
正解率(train): 1.000
正解率(test): 1.000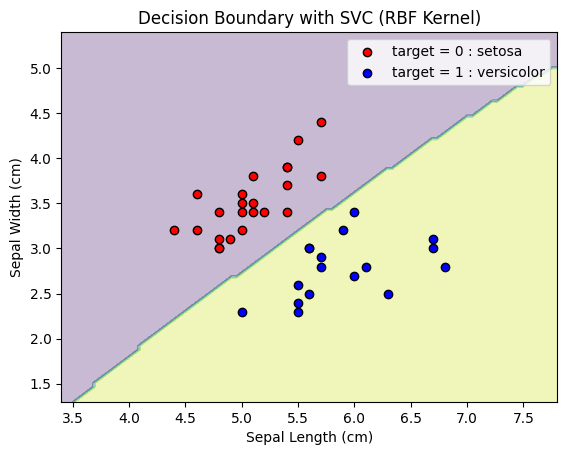

今回のブログでは、SVMの理論背景から、実際のPythonコードによる実装、そして分類平面の可視化までを一通り紹介しました。SVMは、高次元データや複雑なデータにも対応できる汎用的な分類手法で、特にデータのマージンを最大化することで安定した分類が可能となる点が特徴です。

コードを通じて、SVMが実際にどのようにデータを分類し、適切な分類境界を構築するのかを体感いただけたと思います。今回の実装で得られた結果からも、データの特徴をしっかりと捉えたモデル構築ができることが確認できました。


SVMは、データを深く理解し、効率的な分類モデルを設計するための強力なツールです。問題に合わせた適切なカーネルとパラメータの設定が、精度の高い予測を可能にします。

多層パーセプトロン (MLP)

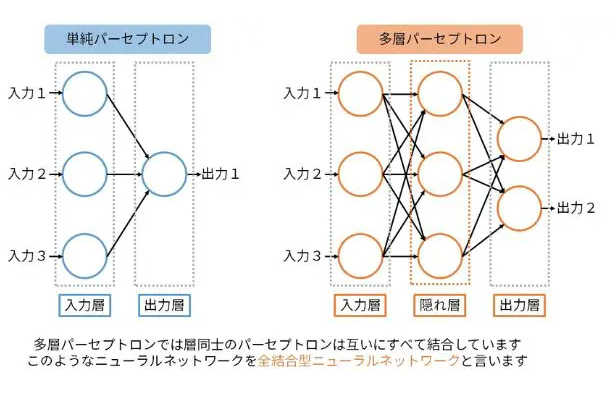
多層パーセプトロン（MLP） は、ニューラルネットワークの最も基本的な形式であり、複数の層（入力層、隠れ層、出力層）から構成されることから「多層」と呼ばれます。各層に配置された複数のニューロン（パーセプトロン）が相互に結合してデータを伝達・処理し、複雑なパターンや非線形な関係を学習する能力を持っています。MLPは、単純な線形分離の限界を超え、例えば画像認識や音声認識、複雑な関数の近似などにも利用されるなど、広い応用範囲を持っています。

MLPの構造と動作

構造とデータフロー：

  • 入力層：各ニューロンは入力データの特徴（ピクセル値、測定値など）を受け取ります。
  • 隠れ層：非線形な関係を捉えるために活性化関数が適用され、複数の隠れ層が存在する場合、次々に伝達されていきます。
  • 出力層：分類タスクであれば各クラスの予測確率を、回帰タスクであれば予測値を出力します。
https://zero2one.jp/ai-word/multilayer-perceptron/

活性化関数

MLPの隠れ層に配置されるニューロンは、入力を受け取り、活性化関数を適用して非線形な出力を生成します。以下は代表的な活性化関数です。

シグモイド関数

$$\sigma(x) = \frac{1}{1 + e^{-x}}$$

特徴：

出力が0から1の範囲に収まり、ニューラルネットワークにおける確率的な解釈に適しています。ただし、大きな入力では勾配消失の問題が生じやすく、学習が遅くなることがあります。

用途：

出力が確率として解釈される場合（例：ロジスティック回帰や出力層における分類タスク）に使用されます。

import numpy as np
import matplotlib.pyplot as plt

# Define sigmoid functions
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# Generate x values
x = np.linspace(-10, 10, 100)

# Calculate y values for each function
y_sigmoid = sigmoid(x)

# Plotting
plt.figure(figsize=(15, 5))

# Sigmoid plot
plt.subplot(1, 3, 1)
plt.plot(x, y_sigmoid, label="Sigmoid", color="blue")
plt.title("Sigmoid Function")
plt.xlabel("x")
plt.ylabel("sigmoid(x)")
plt.grid(True)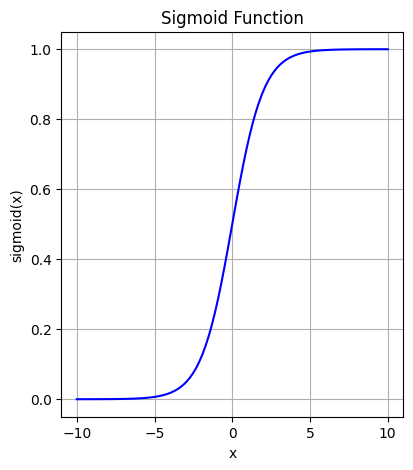
ReLU関数

$$f(x) = \max(0, x)$$

特徴：

入力が正であれば出力がそのまま出力し、負の場合は0を返すため、シンプルで計算効率が高く、深層学習で勾配消失の問題を軽減する効果があります。

用途：

中間層の活性化関数として主に使用され、特に深層ニューラルネットワークでよく用いられます。

import numpy as np
import matplotlib.pyplot as plt

# Define ReLU functions
def relu(x):
    return np.maximum(0, x)

# Generate x values
x = np.linspace(-10, 10, 100)

# Calculate y values for each function
y_relu = relu(x)

# Plotting
plt.figure(figsize=(15, 5))

y_relu = relu(x)

# Plotting
plt.figure(figsize=(15, 5))

# ReLU plot
plt.subplot(1, 3, 2)
plt.plot(x, y_relu, label="ReLU", color="green")
plt.title("ReLU Function")
plt.xlabel("x")
plt.ylabel("ReLU(x)")
plt.grid(True)

plt.tight_layout()
plt.show()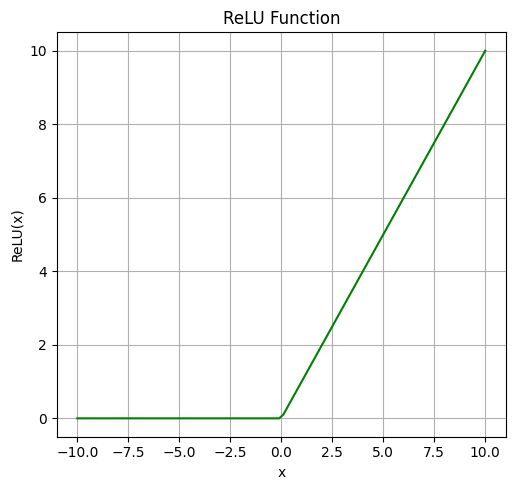
tanh関数

$$\tanh(x) = \frac{e^{x} + e^{-x}}{e^{x} – e^{-x}}$$

特徴：

出力が-1から1の範囲に収まり、シグモイド関数に似ていますが、より広い出力範囲を持つため、勾配消失の影響が若干少なくなります。出力がゼロ中心になるため、学習の収束が速くなることが期待できます。

用途：

回帰や分類タスクの隠れ層で使用されることが多いです。シグモイド関数よりも安定した学習が行われることが多く、LSTMなどのリカレントニューラルネットワーク（RNN）のゲート部分でも用いられます。

import numpy as np
import matplotlib.pyplot as plt

# Define tanh functions
def tanh(x):
    return np.tanh(x)

# Generate x values
x = np.linspace(-10, 10, 100)

# Calculate y values for each function
y_tanh = tanh(x)

# Plotting
plt.figure(figsize=(15, 5))

# tanh plot
plt.subplot(1, 3, 3)
plt.plot(x, y_tanh, label="tanh", color="purple")
plt.title("Tanh Function")
plt.xlabel("x")
plt.ylabel("tanh(x)")
plt.grid(True)

plt.tight_layout()
plt.show()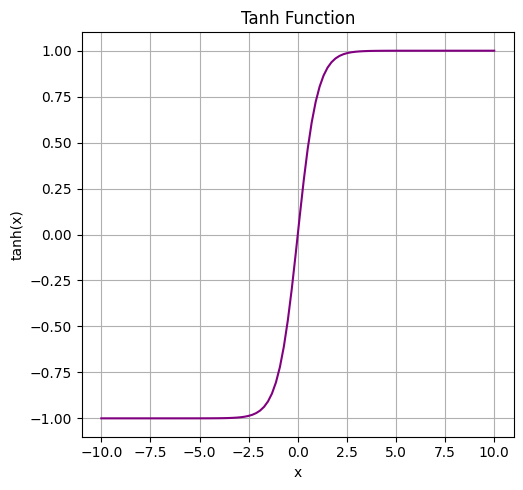

バックプロパゲーション（誤差逆伝播法）

バックプロパゲーションは、MLPの学習過程で、出力層から入力層に向かって損失関数の勾配を逆伝播させ、誤差に基づいて各層の重みを更新する方法です。これにより、各ニューロンの結合強度（重み）を最適化していきます。具体的には、勾配降下法を用いて損失関数の勾配に沿って重みを調整し、損失を最小化します。

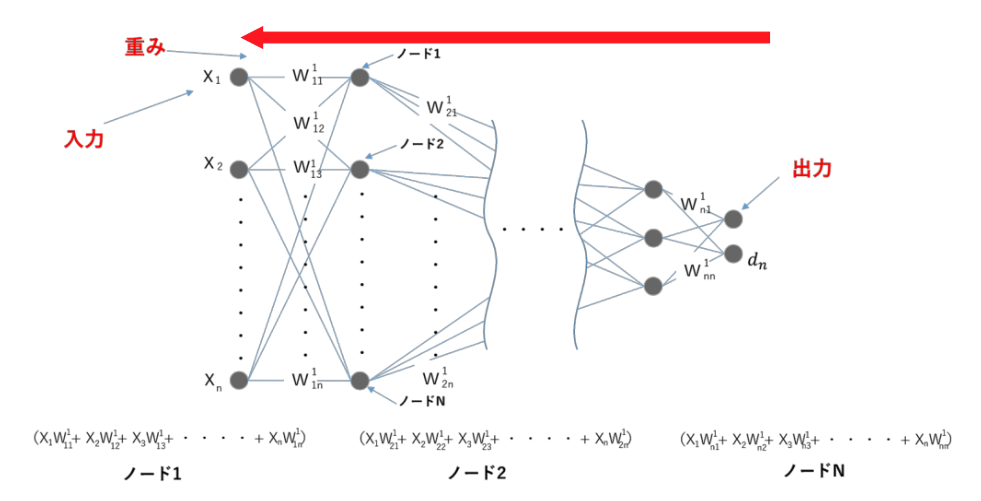
誤差逆伝播法により、モデルが持つ重み $W$ は損失関数 $L$ の勾配 $\frac{\partial L}{\partial W}$ に基づいて更新されます。具体的な手順は以下の通りです。

  1. 順伝播で損失 $L$ を計算。
  2. 出力層から入力層に向かって逆伝播で勾配を計算。
  3. 勾配降下法を用いて、学習率 $η$ に基づき重みを更新。

$$W = W – \eta \frac{\partial L}{\partial W}$$

MLPのメリットとデメリット

メリット：

項目内容
非線形な関係を学習可能複雑なパターンや関係を学習でき、線形モデルでは不可能なパターンも捉えることができます。
汎用性が高い構造や活性化関数、隠れ層の数を調整することで、分類、回帰などさまざまな問題に対応可能です。

デメリット：

項目内容
訓練に時間がかかる特に層が多い場合やデータ量が大きい場合は、学習に時間を要します。
ハイパーパラメータの調整が複雑隠れ層の数、ニューロン数、活性化関数、学習率など、適切なパラメータの設定がモデルの性能に大きな影響を与えます。

多層パーセプトロン（MLP）の実装

Kaggleの “Digit Recognizer” データセットを使用して、手書き数字を識別するためのMLPを実装をします。

from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import pandas as pd
# データの読み込み
df = pd.read_csv('train.csv')

# 列名を確認
print(df.columns)
Index(['label', 'pixel0', 'pixel1', 'pixel2', 'pixel3', 'pixel4', 'pixel5',
       'pixel6', 'pixel7', 'pixel8',
       ...
       'pixel774', 'pixel775', 'pixel776', 'pixel777', 'pixel778', 'pixel779',
       'pixel780', 'pixel781', 'pixel782', 'pixel783'],
      dtype='object', length=785)
# 特徴量とターゲットの分離
X = df.drop('label', axis=1) / 255.0  # ピクセル値を正規化
y = df['label']

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# モデルの定義
mlp = MLPClassifier(hidden_layer_sizes=(100,), activation='relu', solver='adam', max_iter=20, random_state=42)

# モデルの訓練
mlp.fit(X_train, y_train)

# 予測と精度評価
y_pred = mlp.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
Accuracy: 0.97
# 学習曲線の描画
plt.plot(mlp.loss_curve_)
plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.title('Learning Curve')
plt.show()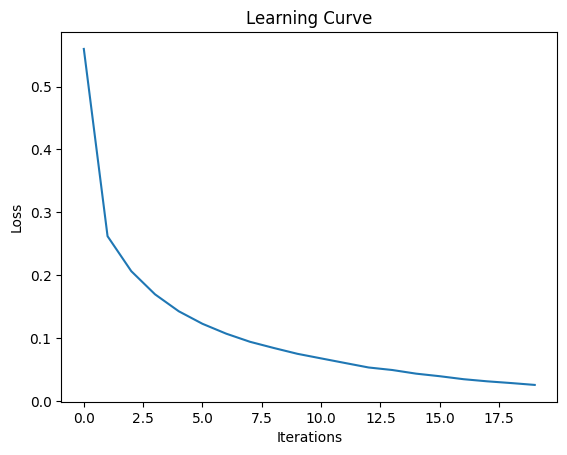

ランダムサーチでハイパーパラメータチューニング：

from sklearn.model_selection import RandomizedSearchCV

param_grid = {
    'hidden_layer_sizes': [(100,)],  # 1つの隠れ層に100ユニットのみ
    'activation': ['relu'],  # 1つのアクティベーション関数のみ
    'solver': ['adam'],  # 1つのソルバーのみ
    'max_iter': [100]  # 最大100回の反復
}

# ランダムサーチの実行
random_search = RandomizedSearchCV(MLPClassifier(random_state=42), param_distributions=param_grid, n_iter=10, cv=5)
random_search.fit(X_train, y_train)

# 最適なパラメータの表示
best_params = random_search.best_params_
print("Best parameters found: ", best_params)
Best parameters found:  {'solver': 'adam', 'max_iter': 100, 'hidden_layer_sizes': (100,), 'activation': 'relu'}

モデルを再学習：

# 最適なパラメータを使ってモデルを再定義
mlp_best = MLPClassifier(
    hidden_layer_sizes=best_params['hidden_layer_sizes'],
    activation=best_params['activation'],
    solver=best_params['solver'],
    max_iter=best_params['max_iter'],
    random_state=42
)

# モデルの再学習
mlp_best.fit(X_train, y_train)

# 予測と精度評価
y_pred_best = mlp_best.predict(X_test)
accuracy_best = accuracy_score(y_test, y_pred_best)
print(f'Accuracy with best parameters: {accuracy_best:.2f}')
Accuracy with best parameters: 0.97

グリッドサーチを用いると実行時間が長くなりますので、今回はランダムサーチを用いることにしました。

実行時間を短くする方法：精度が落ちる可能性があるので注意です。

  • 訓練データのサイズを減らす
  • エポック数を減らす（max_iter の値を減らすことで訓練時間を短縮）
  • GPUの利用（もし可能であれば、GPUを使用して訓練を行うことで、計算時間を大幅に短縮できます。）
  • 早期停止の導入：モデルの訓練中に、検証データの精度が向上しなくなった場合に訓練を停止することで、無駄な計算を省くことができます。
mlp = MLPClassifier(hidden_layer_sizes=(100,), activation='relu', solver='adam', max_iter=200, random_state=42, early_stopping=True, validation_fraction=0.1) # 早期停止の導入

実装結果の分析と学習曲線

精度評価：

テストセットに対して得られる精度が示され、モデルの性能がわかります。特に、手書き数字認識のようなタスクでは、精度がモデルの適合性を評価する主要な指標となります。

学習曲線：

損失関数の値がイテレーションごとに減少する様子をプロットすることで、モデルが適切に収束しているか、過学習や学習不足に陥っていないか確認できます。

多層パーセプトロンは、そのシンプルさから多くの用途で利用される一方で、構造やパラメータ設定により非常に柔軟で応用範囲が広いアルゴリズムです。MLPのような基本的なニューラルネットワークを理解することは、深層学習やさらに複雑なモデルを習得するための重要な基礎となります。

教師あり学習のアルゴリズム比較と適用例

アルゴリズムメリットデメリット主な適用例
k近傍法実装が簡単、非線形データに対応計算量が多い、高次元で性能低下パターン認識、画像分類
ナイーブベイズ計算が高速、少量データでも性能が良い特徴量の独立性仮定が非現実的テキスト分類、スパム検出
決定木解釈性が高い、前処理が少ない過学習しやすい、小さな変動に敏感医療診断、信用リスク評価
ランダムフォレスト高精度、過学習抑制計算コストが高い、解釈性が低い特徴量選択、分類・回帰全般
サポートベクターマシン高次元データに強い、汎化性能が高い計算量が多い、ハイパーパラメータ調整が難しい画像分類、テキスト分類
多層パーセプトロン非線形関係の学習、汎用性が高い訓練時間が長い、調整が複雑音声認識、画像認識、自然言語処理
  • ビジネスの意思決定：決定木を用いて顧客の離反要因を分析し、マーケティング戦略に活用。
  • スパムフィルタリング：ナイーブベイズでメールの内容を分析し、スパムメールを自動分類。
  • 画像認識：MLPやSVMを用いて製品の不良検知を自動化。
  • 顧客セグメンテーション：ランダムフォレストで顧客データを分類し、ターゲットマーケティングを実施。

学習の狙いと次回予告

今回の講義では、教師あり学習の基礎と代表的なアルゴリズムについて学びました。それぞれのアルゴリズムは特有のメリット・デメリットを持ち、適用すべき場面が異なります。重要なのは、問題の性質やデータの特性に合わせて最適なアルゴリズムを選択できるようになることです。

次回は教師なし学習の詳細について解説します。教師なし学習とは、ラベルなしデータからパターンや構造を見つけ出す手法であり、クラスタリングや次元削減などのアルゴリズムを学びます。教師あり学習との違いや、その応用範囲についても深掘りしていきます。

コメント

タイトルとURLをコピーしました