【第6回】線形回帰とロジスティック回帰の実装と最急降下法の役割

目的

このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用できる力を養うことが目的です。この過程で、実践的な演習やプロジェクトを通じて、手を動かしながら学ぶ姿勢を大切にしていきます。

第6回の目標

第6回では、線形回帰とロジスティック回帰の基本的な理論を理解し、これらのモデルを実際に実装する能力を身につけることを目指します。具体的な学習目標は以下の通りです。

線形回帰の理解
- 線形回帰の定義と数学的表現を理解し、特徴量とターゲット変数の関係をモデル化する方法を学ぶ。
- 損失関数（平均二乗誤差）の役割を理解し、最適化の必要性を認識する。
最急降下法の習得
- 最急降下法の基本的な概念と損失関数を最小化するための数式を理解する。
- 勾配の計算方法を学び、最急降下法を用いて重みを更新するプロセスを把握する。
線形回帰の実装
- カリフォルニア州の住宅価格データセットを使用して、Pythonによる線形回帰モデルの実装手法を習得する。
- 最急降下法を用いて重みを更新し、モデルの予測精度を評価する方法を理解する。
ロジスティック回帰の理解
- ロジスティック回帰の定義と数式を理解し、確率的な出力を得るための手法を学ぶ。
- 目的関数（交差エントロピー損失）の役割を理解し、モデルの適用性を認識する。
ロジスティック回帰の実装
- 乳がんの診断データセットとIrisデータセットを用いて、Pythonによるロジスティック回帰モデルの実装手法を習得する。
- 最急降下法を用いて重みを更新し、モデルの分類精度を評価する方法を理解する。
最急降下法のバリエーションの習得
- 確率的勾配降下法やミニバッチ勾配降下法など、最急降下法のバリエーションについて学び、各手法の利点と適用ケースを理解する。
総合的な理解
- 線形回帰とロジスティック回帰における最急降下法の役割を振り返り、次回以降の内容に繋げる準備をする。

はじめに

機械学習における線形回帰とロジスティック回帰は、最も基本的かつ重要なアルゴリズムの一つです。これらのモデルは、データのパターンを学習し、予測や分類を行うための基盤を提供します。そして、これらのモデルを効果的に学習させるための手法として、最急降下法（Gradient Descent）が重要な役割を果たします。本記事では、線形回帰とロジスティック回帰の基本概念から、その実装方法、そして最急降下法によるパラメータの最適化手法について、数式とPythonコードを用いて詳しく解説します。

線形回帰

線形回帰は、入力特徴量と出力との間の線形関係をモデル化する手法です。目的は、与えられたデータセットに最も適合する直線（または高次元では超平面）を見つけることです。

線形回帰

線形回帰は、入力変数 $X$ と出力変数 $y$ の線形関係をモデル化する手法です。モデルの予測値 $\hat{y}$ は、次のように表されます。

$$\hat{y} = w_0 + w_1 X_1 + w_2 X_2 + \ldots + w_n X_n$$

$\hat{y}$：予測値
$w_0$：バイアス項（切片）
$w_i$：各特徴量$X_i$の重み（係数）

このモデルでは、全ての入力特徴量が線形結合され、予測値を生成します。

目的関数（損失関数）

平均二乗誤差（MSE)

モデルの性能を評価するために、平均二乗誤差（Mean Squared Error, MSE）を損失関数として用います。損失関数（MSE）は、予測値と実際の値との誤差を二乗し、その平均を取ることで計算されます。

$$L({w_0}, {w_1}) = \frac{1}{m} \sum_{i=1}^{m} (y_i – \hat{y}_i)^2$$

$L({w_0}, {w_1})$：損失関数（MSE）
$m$：サンプル数
$\hat{y}_{(i)}$：$i$番目の予測値 $({w}_0 + {w}_1{X}_i)$
$y_{(i)}$：$i$番目の実際の値

残差の二乗和が最小になるように線を引く。

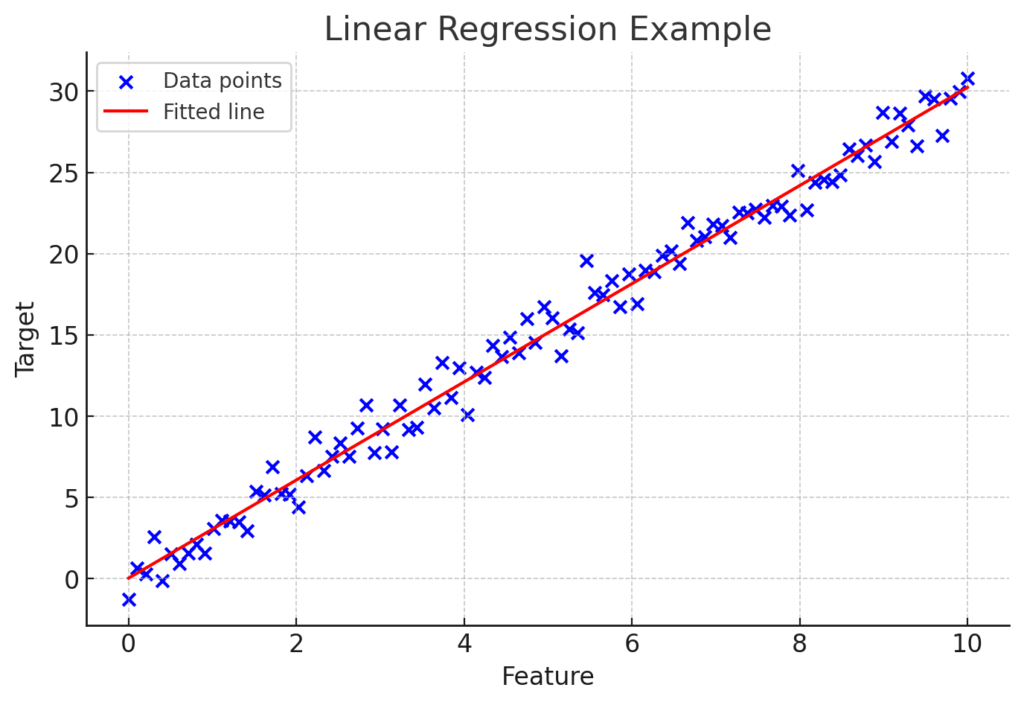
損失関数（MSE)は、モデルが予測した値が実際の値にどれだけ近いかを示す指標であり、値が小さいほどモデルの精度が高いことを意味します。

最急降下法

最急降下法は、損失関数を最小化するための反復最適化アルゴリズムです。パラメータθを更新することで、損失関数の値を徐々に減少させ、最適解に近づけます。また、パラメータθは複数存在する場合も同時に更新していきます。

$$w_0 := w_0 – \alpha \frac{\partial}{\partial w_0} L(w_0, w_1)$$

$$w_1 := w_1 – \alpha \frac{\partial}{\partial w_1} L(w_0, w_1)$$

先ほど紹介した損失関数（MSE)に各々のパラメータを使って微分します。

$$L({w_0}, {w_1}) = \frac{1}{m} \sum_{i=1}^{m} (y_i – \hat{y}_i)^2 = \frac{1}{m} \sum_{i=1}^{m} (y_i – ({w}_0 + {w}_1{X}_i))$$

$w_0$で微分した場合

$$\frac{\partial}{\partial w_0} L(w_0, w_1) = -\frac{2}{m} \sum_{i=1}^{m} \left( y_i – (w_0 + w_1 X_i) \right) = \frac{2}{m} \sum_{i=1}^{m} \left( w_0 + w_1 X_i – y_i \right)$$

$w_1$で微分した場合

$$\frac{\partial}{\partial w_1} L(w_0, w_1) = -\frac{2}{m} \sum_{i=1}^{m} \left( y_i – (w_0 + w_1 X_i) \right) X_i = \frac{2}{m} \sum_{i=1}^{m} \left( w_0 + w_1 X_i – y_i \right) X_i$$

項目	説明
目的	最急降下法は最適化問題の勾配法のアルゴリズムで、損失関数を最小化するための数式。
最も急になる方向	最急降下法では、現在のパラメータにおける目的関数の勾配を計算し、そのベクトルが指し示す方向が最も急に目的関数が減少する方向です。これに基づいて、パラメータを更新します。
局所最適解	最急降下法は、最適化の過程で局所最適解に収束することがあります。これは、全体の最適解ではなく、現在の初期値に依存した最適解です。局所最適解は、周囲の点に比べて目的関数の値が低いですが、グローバル最適解ではない可能性があります。
最適解	最急降下法における最適解は、目的関数が最小になる点を指します。最急降下法は、適切な初期値と学習率を選ぶことで、この最適解に近づくことができます。ただし、初期値の選定によっては局所最適解に留まることもあります。

コーディング例

最急降下法を使って損失関数である線形回帰の数式における最適なパラメータθを見つけます。

data_1 ダウンロード

線形回帰における損失関数（MSE）の定義

import numpy as np
import pandas as pd

df = pd.read_csv('data_1.csv')

x = df['space'].values
y = df['rent'].values

# 描画時にわかりやすいところに初期値を設定
w_0_init = -5
w_1_init = -0.5

# パラメータ更新
def update_w0(w_0, w_1, x, y, alpha=0.05):  # alpha=最急降下法における学習率
    return w_0 - alpha * 2 * np.mean((w_0 + w_1 * x) - y)

def update_w1(w_0, w_1, x, y, alpha=0.05):
    return w_1 - alpha * 2 * np.mean(((w_0 + w_1 * x) - y) * x) 

epochs = 100000
alpha = 0.00005

# パラメータ更新の履歴
w_0_hist = []
w_1_hist = []
# 初期化
w_0_hist.append(w_0_init)
w_1_hist.append(w_1_init)

# 最急降下法
for _ in range(epochs):
    updated_w_0 = update_w0(w_0_hist[-1], w_1_hist[-1], x=x, y=y, alpha=alpha)
    updated_w_1 = update_w1(w_0_hist[-1], w_1_hist[-1], x=x, y=y, alpha=alpha)
    w_0_hist.append(updated_w_0)
    w_1_hist.append(updated_w_1)


# パラメータθの最適解
print(w_0_hist[-1]) # 切片
print(w_1_hist[-1]) # 係数

12.781257525396768　# 最適なパラメータθ₀
0.168328822609761  # 最適なパラメータθ₁

3Dグラフを使って描画

import matplotlib.pyplot as plt
from itertools import product

# 軸の値の数
n0 = n1 = 300

# それぞれのパラメータθの最小値と最大値
min_0 = -20
max_0 = 20
min_1 = -1
max_1 = 1

# 軸の値設定
w_0 = np.linspace(min_0, max_0, n0)
w_1 = np.linspace(min_1, max_1, n1)
# plot_surface用に2次元にする
w_0_ax, w_1_ax = np.meshgrid(w_0, w_1)

# 損失関数の定義
def cost_func(w_0, w_1, x, y):
    return np.mean(np.square(y - (w_0 + w_1 * x)))  # square = 要素の２乗を返す

product(w_0, w_1)
z = [cost_func(param[0], param[1], x=x, y=y) for param in list(product(w_0, w_1))]

# plot_surface用に2次元にする
Z = np.array(z).reshape(n0, n1)

# 損失の推移
cost_hist = [cost_func(*param, x=x, y=y) for param in zip(w_0_hist, w_1_hist)]

ax = plt.axes(projection='3d')
ax.plot(w_0_hist, w_1_hist, cost_hist, 'x-')
ax.plot_surface(w_0_ax.T, w_1_ax.T, Z, cmap='jet', alpha=0.5)
plt.gca().invert_xaxis()
ax.view_init(elev=30, azim=10)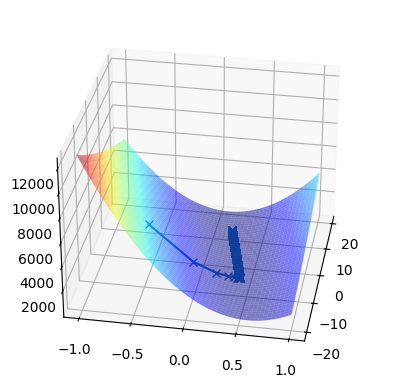

等高線の描画

plt.contour(w_1_ax.T, w_0_ax.T, Z, 100, cmap='jet')
plt.plot(w_1_hist, w_0_hist, 'x-')
plt.xlabel('w 1')
plt.ylabel('w 0')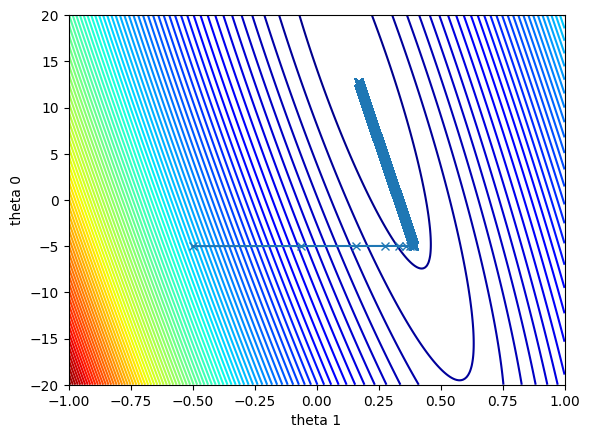

線形回帰の描画

import seaborn as sns
sns.scatterplot(x='space', y='rent', data=df)
x_values = np.arange(120)
y_values = w_0_hist[-1] + w_1_hist[-1]*x_values
plt.plot(x_values, y_values, '-', color='r')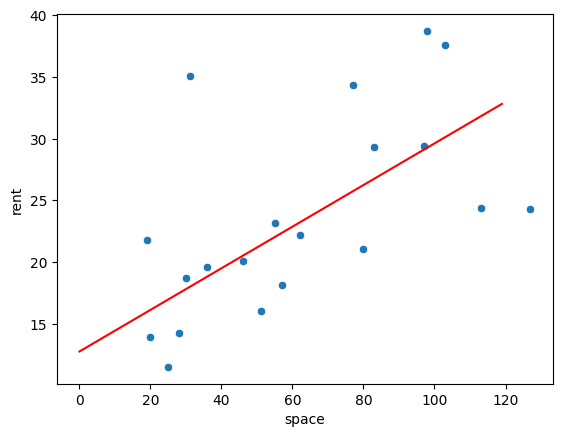

線形回帰の実装

まず、カリフォルニア州の住宅価格データセットを用いて、特徴量から住宅価格を予測するモデルを構築します。

ライブラリのインポート

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import StandardScaler

データの読み込みと前処理

# データの読み込み
housing = fetch_california_housing()
X = housing.data
y = housing.target 

# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# バイアス項を追加
X_scaled = np.c_[np.ones(X_scaled.shape[0]), X_scaled]

パラメータの初期化

# パラメータの初期化
np.random.seed(42)
w = np.random.randn(X_scaled.shape[1])

最急降下法による重みの更新

# ハイパーパラメータ
alpha = 0.01  # 学習率
epochs = 1000  # エポック数
m = y.size  # サンプル数

# 損失を記録するリスト
loss_history = []

for epoch in range(epochs):
    # 予測値の計算
    y_pred = X_scaled.dot(w)
    
    # 損失の計算
    loss = (1/(2*m)) * np.sum((y_pred - y) ** 2)
    loss_history.append(loss)
    
    # 勾配の計算（偏微分）
    gradient = (1/m) * X_scaled.T.dot(y_pred - y)
    
    # パラメータの更新
    w -= alpha * gradient

    # 進捗の表示
    if epoch % 100 == 0:
        print(f"Epoch {epoch}, Loss: {loss:.4f}")

Epoch 0, Loss: 4.9604
Epoch 100, Loss: 0.8621
Epoch 200, Loss: 0.4748
Epoch 300, Loss: 0.4057
Epoch 400, Loss: 0.3791
Epoch 500, Loss: 0.3609
Epoch 600, Loss: 0.3459
Epoch 700, Loss: 0.3333
Epoch 800, Loss: 0.3226
Epoch 900, Loss: 0.3135

結果の可視化

plt.plot(loss_history)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Loss Curve')
plt.show()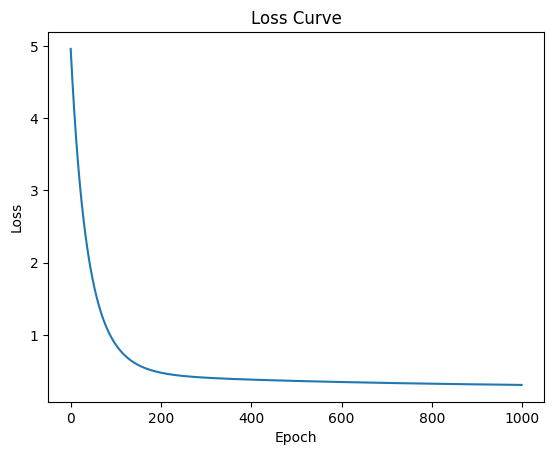

学習後のパラメータ（切片と係数）を出力

# 学習後のパラメータ（切片と係数）を出力
intercept = w[0]  # バイアス項（切片）
coefficients = w[1:]  # 係数

print(f"Intercept: {intercept:.4f}")
print(f"Coefficients: {coefficients}")

Intercept: 2.0685
Coefficients: [ 0.63677248  0.19882355  0.31637146 -0.27123816  0.02702369 -0.04189832
 -0.49607897 -0.43375306]

ここまででは最適なパラメータと係数がわからないので次は最適なパラメータと係数を求めます。

最適なハイパーパラメータと係数の求め方の別の例

グリッドサーチで探索するハイパーパラメータとその候補値を指定する記述を行い、最適なパラメータと係数を導き出します。その後その数値を基にMSEで損失関数を出します。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# データの読み込み
housing = fetch_california_housing()
X = housing.data
y = housing.target

# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# バイアス項を追加
X_scaled = np.c_[np.ones(X_scaled.shape[0]), X_scaled]

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# 線形回帰モデル
model = LinearRegression()

# ハイパーパラメータの候補
param_grid = {'fit_intercept': [True, False]}  # 切片を含めるかどうか

# グリッドサーチと交差検証
grid_search = GridSearchCV(model, param_grid, cv=5, scoring='neg_mean_squared_error')
grid_search.fit(X_train, y_train)

# 最適なハイパーパラメータと係数
print("最適なハイパーパラメータ:", grid_search.best_params_)
print("最適な係数:", grid_search.best_estimator_.coef_)
print("最適な切片:", grid_search.best_estimator_.intercept_)  # 切片を出力

# テストデータで評価
y_pred = grid_search.predict(X_test)
mse = mean_squared_error(y_test, y_pred)  
print("テストデータの平均二乗誤差:", round(mse, 4)) # MSEを小数点以下4桁で丸める

最適なハイパーパラメータ: {'fit_intercept': False}
最適な係数: [ 2.06786231  0.85238169  0.12238224 -0.30511591  0.37113188 -0.00229841
 -0.03662363 -0.89663505 -0.86892682] 
最適な切片: 0.0.   # 最適な切片は最適な係数の一番目である2.06786...
テストデータの平均二乗誤差: 0.5559

ロジスティック回帰

ロジスティック回帰は、二値分類問題を扱うためのモデルです。ロジスティック回帰は、線形回帰を分類問題に拡張したもので、シグモイド関数を用いて出力を0から1の範囲に収めます。

ロジスティック回帰において、シグモイド関数への入力 $z$は、説明変数（特徴量）の線形結合として求められます。この $z$ をシグモイド関数に通すことで、出力が0から1の確率として解釈可能な値に変換されます。

シグモイド関数（二値分類）

シグモイド関数への入力$z$の求め方

$$z = w_0 + w_1 X_1 + w_2 X_2 + \ldots + w_n X_n$$

$w_0$ はバイアス項（切片）
$w_1 + w_2 + \ldots + w_n$ は特徴量に対応する重み（係数）
$X_1 + X_2 + \ldots + x_n$ は各特徴量です。

各特徴量 $X$ に重み $w$ を掛けて合計し、バイアス項 $w_0$ を加えたものが $z$ になります。

シグモイド関数

シグモイド関数 $σ(z)$ は、次のように $z$ を0から1の範囲に変換します。

$$\sigma(z) = \frac{1}{1 + e^{-z}}$$

よって、ロジスティック回帰モデルの予測確率 $\hat{y}$ は次のように書けます。

$$\hat{y} = \sigma(z) = \frac{1}{1 + e^{-(w_0 + w_1 X_1 + w_2 X_2 + \ldots + w_n X_n)}}$$

この $z$ の式が、シグモイド関数への入力としてロジスティック回帰の分類結果を確率として表すための基本式となります。

目的関数（損失関数）

ロジスティック回帰では、二値クロスエントロピー誤差を使用します。

二値クロスエントロピー誤差

$$L(w_0, w_1) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y_{i} \log(\hat{y}_{i}) + (1 – y_{i}) \log(1 – \hat{y}_{i}) \right]$$

ロジスティック回帰の実装

二値分類

乳がんの診断データセットを使用してロジスティック回帰の二値分類を実装します。

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd

# 乳がんデータセットの読み込み
cancer = load_breast_cancer()
df = pd.DataFrame(cancer.data, columns=cancer.feature_names)
df['target'] = cancer.target

X = df  # DataFrame df を説明変数として使用
y = df['target']


# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ロジスティック回帰モデルの作成
model = LogisticRegression(max_iter=200)
model.fit(X_train, y_train)

# 予測
y_pred = model.predict(X_test)

# 精度の計算
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')

Accuracy: 1.00

予測値：

y_pred

array([1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1,
       0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1,
       1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1,
       0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0,
       1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1,
       0, 1, 1, 0])

予測確率：

# 左：0と右：1の値が表示される。確率の値で足して1になる値。大きい値がy_predで表示される。
y_pred_proba = model.predict_proba(X_test) 
y_pred_proba[:5]

array([[4.02183880e-02, 9.59781612e-01],
       [9.99999968e-01, 3.20011761e-08],
       [9.98860243e-01, 1.13975670e-03],
       [1.73533624e-03, 9.98264664e-01],
       [6.02923028e-04, 9.99397077e-01]])

損失関数：

from sklearn.metrics import log_loss
log_loss(y_test, y_pred_proba)

0.014699950041688458

係数($w_1$)：

# coefficient   係数の値（w1の係数Xの値）を確認できる
model.coef_

array([[ 8.93626420e-01,  2.14320057e-02,  4.41424366e-02,
        -4.21124154e-04, -4.63793112e-02, -1.67627796e-01,
        -2.51495371e-01, -1.22312997e-01, -6.78417479e-02,
        -1.17787851e-02, -1.16150567e-03,  5.13390811e-01,
        -7.51219983e-02, -5.45028443e-02, -4.61342009e-03,
        -1.74279056e-02, -3.47260046e-02, -1.47343585e-02,
        -1.52915207e-02, -1.40310258e-04,  7.08366848e-01,
        -2.08387353e-01, -9.05156155e-02, -1.67490147e-02,
        -8.33188463e-02, -5.00831631e-01, -6.56343396e-01,
        -2.22549070e-01, -2.32426942e-01, -4.71322653e-02,
         4.30613648e+00]])

切片（$w_0$)：

# intercept 切片の確認ができる（w0の値）
model.intercept_

array([0.29481939])

クラスの確認：

# classes  # クラス名の確認
model.classes_

array([0, 1])

多項ロジスティック回帰：多クラス分類

多項ロジスティック回帰は、出力クラスごとのスコア（線形結合）を計算し、それらをシグモイド関数の代わりにソフトマックス関数で変換することで、各クラスに属する確率を求めます。

各クラス $k$ に対するスコア $z_k$ は次のように計算されます。

$$z_k = w_{0,k} + w_{1,k} X_1 + w_{2,k} X_2 + \ldots + w_{n,k} X_n$$

$w_j,_k$ はクラス $k$ に対応する特徴量 $j$ の重み。
$X_j$ は特徴量。

ソフトマックス関数はシグモイド関数を一般化したものである。

$$\sigma(z) = \frac{1}{1 + e^{-z}}$$

$$1 – \sigma(z) = 1 – \frac{1}{1 + e^{-z}}$$

$z = z_1(positive) – z_2(negative)$ → 今までは$z_2 = 0$としていた

$$\sigma(z) = \frac{1}{1 + e^{-(z_1-z_2)}} = \frac{1}{1 + \frac{e^z_2}{e^z_1}} =\frac{e^z_1}{e^z_1 + e^z_2}$$

$$1 – \sigma(z) = 1 – \frac{1}{1 + e^{-(z_1-z_2)}} = \frac{e^z_1 + e^z_2}{e^z_1 + e^z_2} – \frac{e^z_1}{e^z_1 + e^z_2} = \frac{e^z_2}{e^z_1 + e^z_2}$$

そして、各クラス $k$ に対する確率 $P_k(z)$ は、ソフトマックス関数を用いて以下のように計算します。

$$P_k(z) = \frac{e^z_k}{e^z_1 + e^z_2 + \ldots + e^z_K} = \frac{e^{z_k}}{\sum_{k=1}^{K} e^{z_k}}$$

$$P_k(z) = \frac{e^{w_0^{(k)} + w_1^{(k)}z}}{\sum_{j=1}^{K} e^{w_0^{(k)} + w_1^{(k)}z}}$$

$K$ はクラスの総数。
分母の合計により、すべてのクラスの確率が0から1の範囲に収まり、合計が1になります。

目的関数（損失関数）

多項ロジスティック回帰では、クロスエントロピー誤差を使用します。

クロスエントロピー誤差

多クラスロジスティック回帰で使用する損失関数は、クロスエントロピー損失（あるいは対数損失）です。各クラスに対するクロスエントロピー損失は次のように定義されます。

$$L(w) = -\frac{1}{m} \sum_{i=1}^{m} \sum_{k=1}^{K} t_ik \log(p_k{(z_i))}$$

この式における$t_ik$は、クラス $k$ に対する「ターゲットラベル」を表します。

$t_ik$ は、サンプル $i$ がクラス $k$ に属している場合に 1、そうでない場合に 0 となる「ターゲットラベル」の指標です。
損失関数では、正しいクラスに属する予測確率のみに対して影響を与える役割を担い、多クラス分類問題でクロスエントロピー損失を用いる際の重要な要素です。

多項ロジスティック回帰の実装

多クラスロジスティック回帰（ソフトマックス回帰）をPythonで実装する際は、一般的にScikit-Learnなどのライブラリが便利です。以下は、Scikit-Learnを使ったソフトマックス回帰の実装例です。

多項ロジスティック回帰では、Irisデータセットを使用して多項ロジスティック回帰を実装します。このデータセットには、アイリスの花の特徴が含まれており、これを用いて花の種類を分類します。

irisのデータセットは2種類あり、今回はseabornからロードできるタイプのirisのデータセットを用いて説明します。

# データ準備
import seaborn as sns
df = sns.load_dataset('iris')

# データの統計量（データ数を確認)
df.describe()


sepal_length	sepal_width	petal_length	petal_width
count	150.000000	150.000000	150.000000	150.000000
mean	5.843333	3.057333	3.758000	1.199333
std	0.828066	0.435866	1.765298	0.762238
min	4.300000	2.000000	1.000000	0.100000
25%	5.100000	2.800000	1.600000	0.300000
50%	5.800000	3.000000	4.350000	1.300000
75%	6.400000	3.300000	5.100000	1.800000
max	7.900000	4.400000	6.900000	2.500000

# 目的変数
df['species'].unique()

array(['setosa', 'versicolor', 'virginica'], dtype=object)

# データの分布描画
sns.pairplot(df, hue='species')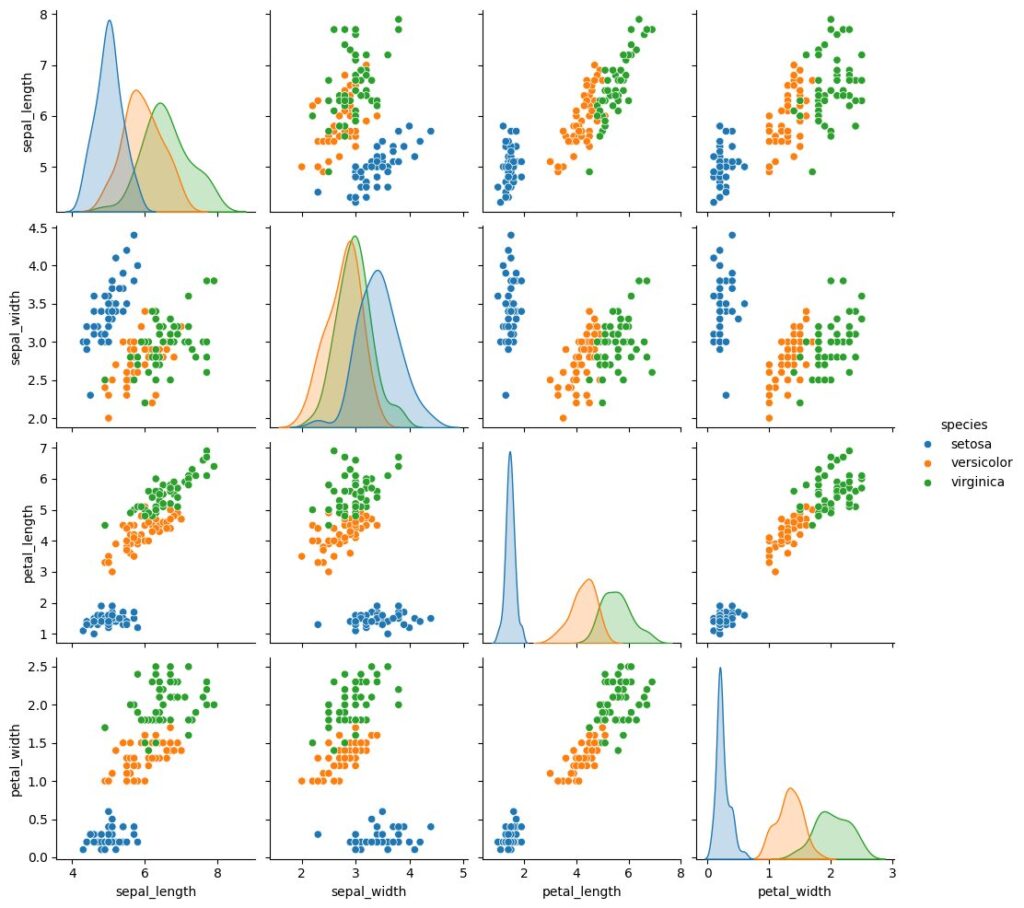

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

y_col = 'species'

X = df.loc[:, df.columns!= y_col]
y = df[y_col]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
print(len(X_train), len(X_test))

105 45

ovr (One-vs-Rest)を使った方法：

model = LogisticRegression(penalty=None, multi_class='ovr')
model.fit(X_train, y_train)
print(model.classes_)  # クラスの位置
print(model.intercept_)  # 切片（w0の値）
print(model.coef_)  # 係数（wの係数であるxの値）

['setosa' 'versicolor' 'virginica']
[   0.80027367    6.81622157 -194.66125661]
[[   1.31884632    4.89432922   -7.72517864   -3.55986105]
 [  -0.41630114   -2.43495253    1.48711273   -3.08253349]
 [-274.4189735  -214.60580483  415.06817579  277.64157221]]

予測確率：

y_pred_proba= model.predict_proba(X_test)
y_pred_proba[:10]

array([[5.75453075e-012, 8.84968012e-002, 9.11503199e-001],
       [3.62381185e-007, 9.99999638e-001, 1.07994282e-163],
       [9.85924766e-001, 1.40752344e-002, 0.00000000e+000],
       [3.64037276e-014, 3.86844342e-001, 6.13155658e-001],
       [8.87503606e-001, 1.12496394e-001, 0.00000000e+000],
       [8.85005473e-014, 6.32465033e-002, 9.36753497e-001],
       [9.44766645e-001, 5.52333554e-002, 0.00000000e+000],
       [2.03065067e-007, 9.99999797e-001, 5.68647796e-144],
       [1.69329646e-008, 9.99999983e-001, 2.80781099e-122],
       [6.51277375e-006, 9.99993487e-001, 5.66906781e-195]])

予測：

y_pred = model.predict(X_test)
y_pred[:10]

array(['virginica', 'versicolor', 'setosa', 'virginica', 'setosa',
       'virginica', 'setosa', 'versicolor', 'versicolor', 'versicolor'],
      dtype=object)

精度：

from sklearn.metrics import accuracy_score
# 精度の計算
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')

Accuracy: 0.96

multinomialを使った方法：

model = LogisticRegression(penalty=None, multi_class='multinomial')
model.fit(X_train, y_train)
print(model.classes_)  # クラスの位置
print(model.intercept_)  # 切片（w0の値）
print(model.coef_)  # 係数（wの係数であるxの値）

['setosa' 'versicolor' 'virginica']
[  50.23483867   80.89212279 -131.12696146]
[[  97.52086048  224.59110511 -327.79332373 -155.24231093]
 [  73.70951969   -9.73352526  -25.53606504  -57.12601799]
 [-171.23038017 -214.85757984  353.32938877  212.36832891]]

予測確率：

y_pred_proba_mn = model.predict_proba(X_test)
y_pred_proba_mn[:10]

array([[0.00000000e+000, 2.81903424e-162, 1.00000000e+000],
       [8.54039479e-296, 1.00000000e+000, 7.52095235e-152],
       [1.00000000e+000, 2.08782726e-279, 0.00000000e+000],
       [0.00000000e+000, 5.00643643e-121, 1.00000000e+000],
       [1.00000000e+000, 1.07113110e-179, 0.00000000e+000],
       [0.00000000e+000, 2.46035151e-224, 1.00000000e+000],
       [1.00000000e+000, 7.25534025e-212, 0.00000000e+000],
       [3.67986794e-310, 1.00000000e+000, 8.60194290e-133],
       [0.00000000e+000, 1.00000000e+000, 5.91823475e-112],
       [1.74469020e-246, 1.00000000e+000, 7.94499211e-181]])

予測：

y_pred_mn = model.predict(X_test)
y_pred_mn

array(['virginica', 'versicolor', 'setosa', 'virginica', 'setosa',
       'virginica', 'setosa', 'versicolor', 'versicolor', 'versicolor',
       'virginica', 'versicolor', 'versicolor', 'versicolor',
       'versicolor', 'setosa', 'versicolor', 'versicolor', 'setosa',
       'setosa', 'virginica', 'versicolor', 'setosa', 'setosa',
       'versicolor', 'setosa', 'setosa', 'versicolor', 'versicolor',
       'setosa', 'virginica', 'versicolor', 'setosa', 'virginica',
       'virginica', 'versicolor', 'setosa', 'virginica', 'versicolor',
       'versicolor', 'virginica', 'setosa', 'virginica', 'setosa',
       'setosa'], dtype=object)

精度：

from sklearn.metrics import accuracy_score
# 精度の計算
accuracy = accuracy_score(y_test, y_pred_mn)
print(f'Accuracy: {accuracy:.2f}')

Accuracy: 0.96

OvRとMultinomialの比較

特徴	説明
One-vs-Rest (OvR)	各クラスに対して、そのクラスとそれ以外のクラスを区別する2クラス分類問題を構築し、複数の2クラス分類器を組み合わせることで多クラス分類を行います。
Multinomial	すべてのクラスを同時に考慮して、各サンプルがどのクラスに属するかを確率的に予測します。

最急降下法の他のバリエーション

確率的勾配降下法（SGD）

サンプルの選択：

SGDでは、データセットからランダムに1つのサンプルを選び、そのサンプルに基づいてパラメータを更新します。

勾配の計算：

選ばれたサンプルに対する損失関数の勾配を計算し、その勾配に従ってパラメータを更新します。

$$w = w – \alpha \nabla J(w： X_{i}, y_{i})$$

$w$：モデルのパラメータ
$α$：学習率
$∇J(w：X_i, y_i)$選ばれたサンプル $X_i,y_i$ に対する損失関数の勾配

利点：

特徴	内容
計算コスト	各更新が非常に早いため、計算コストが低く、大規模データに対して適しています。
早期収束	ランダム性により、局所的な最適解から抜け出しやすく、早期に収束する場合があります。

欠点：

特徴	内容
ノイズの影響	各更新がノイズの影響を受けやすく、最適解に達するまでの道のりが不安定になることがあります。

動作イメージ

SGDは、最適化アルゴリズムの基本的な手法で、パラメータを勾配の方向に沿って更新します。SGDはシンプルで計算コストが低いですが、モメンタムを利用しない場合、収束が遅かったり、振動しやすい特徴があります。

import numpy as np
import matplotlib.pyplot as plt

def func(x, y):
    """二次関数（楕円形状）の定義"""
    return 0.1 * x**2 + y**2

def grad_func(x, y):
    """関数の勾配を計算"""
    grad_x = 0.2 * x
    grad_y = 2 * y
    return np.array([grad_x, grad_y])

def sgd_optimization(x_init, y_init, learning_rate=0.1, steps=50):
    """SGD最適化の実行"""
    x, y = x_init, y_init
    trajectory = [(x, y)]
    
    for _ in range(steps):
        grad = grad_func(x, y)
        x, y = x - learning_rate * grad[0], y - learning_rate * grad[1]
        trajectory.append((x, y))
    
    return np.array(trajectory)

def plot_contour_with_trajectory(func, trajectory, levels=20):
    """等高線と最適化の軌跡をプロット"""
    x_range = np.linspace(-10, 10, 400)
    y_range = np.linspace(-10, 10, 400)
    X, Y = np.meshgrid(x_range, y_range)
    Z = func(X, Y)
    
    plt.figure(figsize=(10, 8))
    contour = plt.contour(X, Y, Z, levels=levels, cmap="cool")
    plt.clabel(contour, inline=True, fontsize=8)
    
    # 軌跡のプロット
    plt.plot(trajectory[:, 0], trajectory[:, 1], 'bo-', markersize=5, label="SGD Path")
    
    # 初期点と最終点のマーカー
    plt.scatter(trajectory[0, 0], trajectory[0, 1], color='green', s=100, label='Start')
    plt.scatter(trajectory[-1, 0], trajectory[-1, 1], color='blue', s=100, label='End')
    
    plt.title("SGD Optimization Trajectory")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.legend()
    plt.grid(True)
    plt.show()

# パラメータの設定
learning_rate = 0.1
steps = 50
x_init, y_init = -8.0, 4.0

# 最適化の実行
trajectory = sgd_optimization(x_init, y_init, learning_rate, steps)

# プロットの作成
plot_contour_with_trajectory(func, trajectory)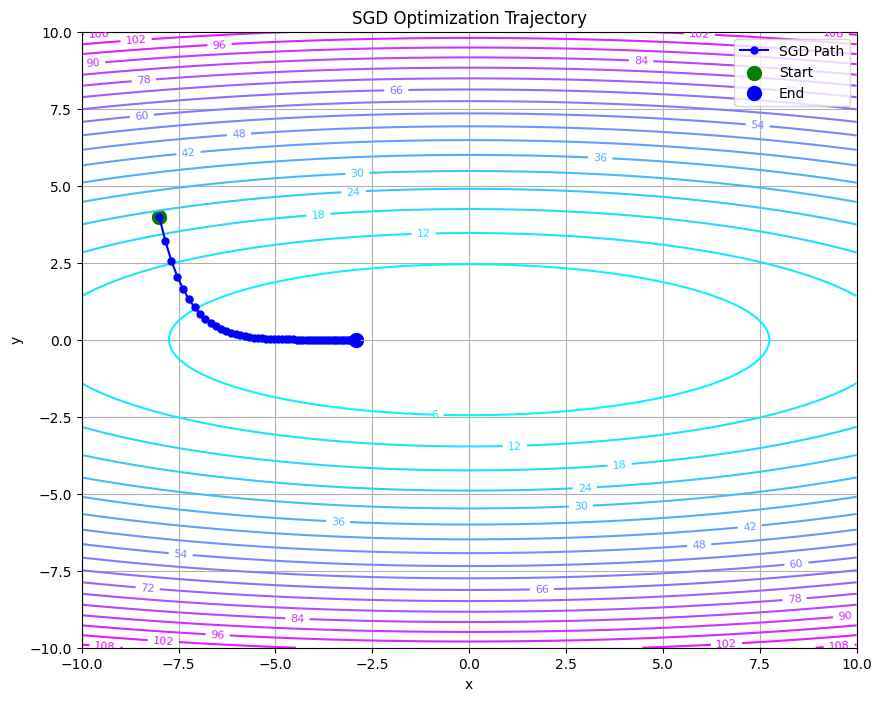

SGDのコーディング例（PyTorch）：

SGDはPyTorchのtorch.optim.SGD（確率的勾配降下法）オプティマイザに対する設定として使用できます。

import torch.optim as optim

# SGDオプティマイザの設定
optimizer = optim.SGD(model.parameters(), lr=0.01)

ミニバッチ勾配降下法

バッチの作成：

データセットを小さなバッチに分割し、各バッチごとに勾配を計算します。この手法は、SGDとバッチ勾配降下法の中間的な挙動を示します。

$$w = w – \alpha \nabla J(w : B)$$

$B$：ミニバッチのサンプル

利点：

特徴	内容
安定性	小さなバッチを使用することで、勾配の計算が安定し、SGDよりも収束がスムーズになる傾向があります。
計算効率	一度に複数のサンプルを使用するため、計算資源の効率が向上します。特にGPUを使用する際に有利です。

欠点：

特徴	内容
バッチサイズの選択	バッチサイズによってモデルの学習が大きく変わるため、適切なサイズを見つける必要があります。

Adam（Adaptive Moment Estimation）

Adamは、勾配降下法を拡張したアルゴリズムで、学習率を各パラメータごとに調整します。過去の勾配を考慮し、勾配の一次モーメント（平均）と二次モーメント（分散）を利用します。

一次モーメントの更新式：

$$m_t = \beta_1 m_{t-1} + (1 – \beta_1) g_t$$

バイアス補正された一次モーメント：

$$\hat{m}_t = \frac{m_t}{1 – \beta_1^t}$$

二次モーメントの推定値：

$$v_t = \beta_2 v_{t-1} + (1 – \beta_2) g_t^2$$

バイアス補正を考慮した推定値：

$$\hat{v}_t = \frac{v_t}{1 – \beta_2^t}$$

重みの更新式

$$w_{t+1} = w_t – \alpha \frac{\hat{m}}{\sqrt{\hat{v} + \epsilon}}$$

特徴	表記	説明
勾配の一次モーメント	$m_t$	勾配の一次モーメント
勾配の二次モーメント	$v_t$	勾配の二次モーメント
現在の勾配	$g_t$	現在の勾配
モーメントの減衰率	$\beta_1, \beta_2$	モーメントの減衰率（通常 (\beta_1 = 0.9, \beta_2 = 0.999)）
ゼロ割りを防ぐための小さな値	$\epsilon$	ゼロ割りを防ぐための小さな値（通常 (1 \times 10^{-8})）

このようにして、Adam最適化アルゴリズムでは、勾配の一次および二次モーメントを更新し、バイアス補正を行うことで、各パラメータに対する適応的な学習率を計算します。これにより、学習の安定性と効率が向上します。

利点：

特徴	内容
自動的な学習率調整	各パラメータに対する学習率を適応的に調整するため、収束が速く、安定性が向上します。
効果的な収束	Adamは多くのデータセットで良い結果を得やすく、特に非定常な目的関数に対して効果的です。

動作イメージ

Adamでは、等高線プロット上で滑らかに最小値へ収束する経路が観察されます。各ステップの更新量は矢印で示され、パラメータの移動方向と大きさが視覚的に理解できます。一階および二階モーメントを利用し、各パラメータごとに適応的な学習率を調整することで、安定した収束が期待できます。

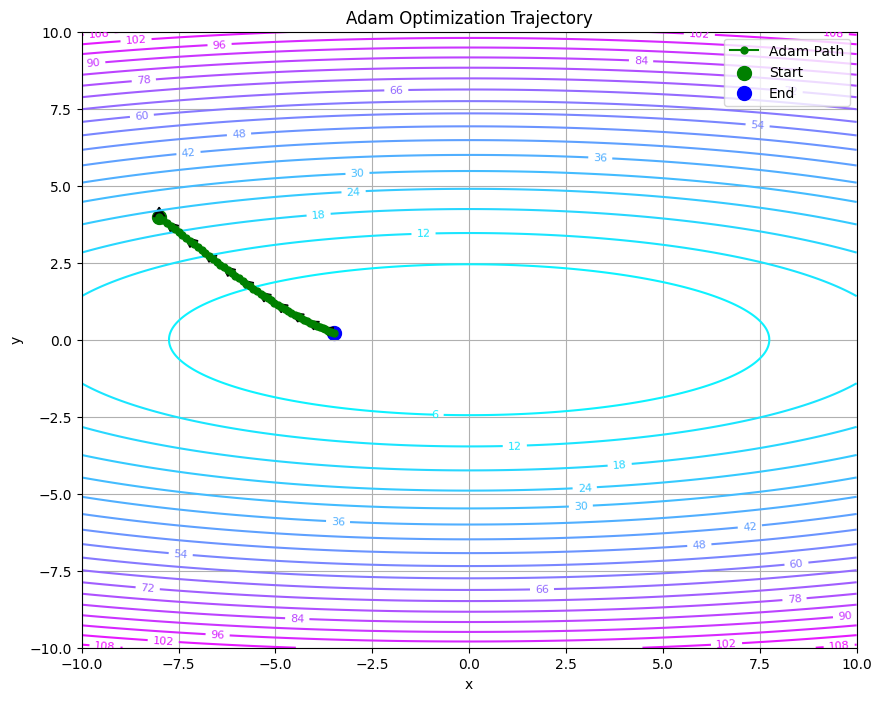
Adamのコーディング例（PyTorch）：

import torch.optim as optim

# Adamオプティマイザの設定
optimizer = optim.Adam(model.parameters(), lr=0.01)

他の最適化アルゴリズム

RMSprop：

学習率を適応的に調整し、最近の勾配の平均を考慮する。

AdaGrad：

各パラメータの更新履歴を利用して学習率を調整するが、更新が進むにつれて学習率が急激に減少する欠点があります。

次回予告

本記事では、線形回帰とロジスティック回帰の基本概念から、そのPythonによる実装、そして最急降下法を用いたパラメータの最適化手法について詳しく解説しました。最急降下法は、機械学習モデルの学習において中心的な役割を果たし、その理解は他の高度なアルゴリズムや最適化手法を学ぶ上での基盤となります。

次回は、教師あり学習の理論と具体例を掘り下げ、サポートベクターマシン（SVM）、決定木、ランダムフォレスト、勾配ブースティングなど、代表的な監視学習アルゴリズムについて詳しく学んでいきます。これにより、実際のデータに対してどのようにこれらの手法を適用するかを理解し、機械学習の応用力を高めていきましょう。

お楽しみに！