第3回の目標
第3回では、データの前処理と可視化に関する基本的な技術を習得し、データの品質を向上させることで機械学習モデルの性能を最大限に引き出す方法を学びます。本ブログでは、データのクリーニングから特徴量エンジニアリングまでを体系的に理解し、データ分析で実際にこれらの技術を応用できる能力を身につけることを目指します。
生データを効果的に変換し、機械学習モデルが最大限に活用できるようにすることは、データサイエンティストとして不可欠なスキルです。データの前処理では、欠損値の処理、不整合なデータ型の修正、スケーリングなどの問題に対処する重要なステップを学びます。また、可視化を通じてデータのパターンやトレンド、潜在的な関係性を明らかにし、洞察に満ちたモデル構築の基盤を築きます。
この記事では、すべてのスキルレベルの読者が理解しやすく、実践できるように、実際の例とPythonコードを用いて具体的に説明します。これにより、データの前処理と可視化の技術を確実に身につけ、実践的なデータサイエンスのスキルを向上させることができるでしょう。
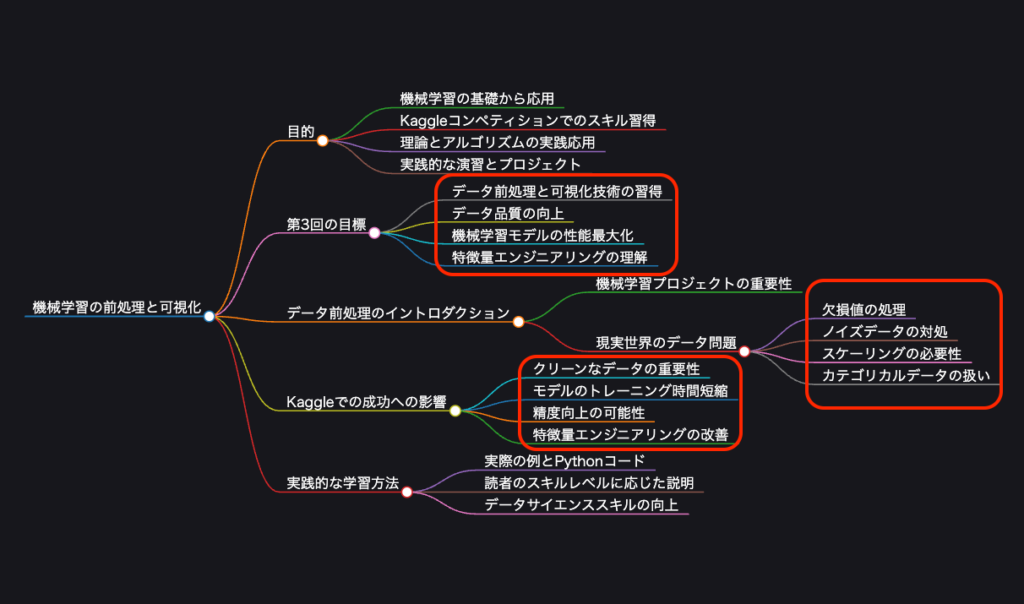
データ前処理のイントロダクション
データ前処理は、機械学習プロジェクトの成功に不可欠なステップです。現実世界のデータは、しばしば以下のような問題を含んでいます。
- 欠損値:データが完全ではない。
- ノイズデータ:異常値や誤ったデータ。
- スケーリングされていない特徴量:異なる尺度の特徴量が混在。
- カテゴリカルデータ:数値でないデータ。
これらの問題を適切に処理しないと、モデルの性能が著しく低下する可能性があります。効果的な前処理は、データの質を向上させ、モデルの精度を高めるために不可欠です。
Kaggleでの成功への影響:
- クリーンなデータは、モデルのトレーニング時間を短縮し、精度を向上させます。
- データの理解が深まることで、より良い特徴量エンジニアリングが可能になります。
欠損値の処理
欠損値の確認
まず、データセットに欠損値が存在するかを確認します。
import pandas as pd
# データの読み込み
df = pd.read_csv('employee_data.csv')
# データの確認
print("元のデータ:")
print(df)
# 欠損値の確認
print("\n欠損値の数:")
print(df.isnull().sum())データをダウンロードし、テキストファイルで実行するとデータの欠損値が出力されます。
欠損値の処理方法
欠損値の削除
欠損値を含む行または列を削除。
行の削除
欠損値を含む行全体を削除します。データが大幅に減少する可能性があるため、注意が必要です。
import pandas as pd
# 欠損値を含む行を削除
df_drop_rows = df.dropna()
print("\n欠損値を含む行を削除したデータ:")
print(df_drop_rows)
# 欠損値の確認
print("\n削除後の欠損値の数:")
print(df_drop_rows.isnull().sum())出力するとデータの欠損値の行が削除されたことが分かります。
列の削除
欠損値が多い列を削除します。例えば、Gender 列の欠損値が1つであれば削除は避けるべきですが、例として Salary 列に対して削除を行います。
import pandas as pd
# Salary列に欠損値があるため削除
df_drop_columns = df.drop(columns=['Salary'])
print("\nSalary列を削除したデータ:")
print(df_drop_columns)
# 欠損値の確認
print("\n削除後の欠損値の数:")
print(df_drop_columns.isnull().sum())出力するとSalary列のデータが削除されたことが分かります。
欠損値の補完
欠損値を削除せずに、他の値で埋める方法です。ここでは、平均値、中央値、最頻値、そして機械学習モデルを用いた補完方法を紹介します。
平均値での補完
数値データの欠損値を平均値で埋めます。
import pandas as pd
# Age列の平均値で補完
age_mean = df['Age'].mean()
df['Age_mean_imputed'] = df['Age'].fillna(age_mean)
# Salary列の平均値で補完
salary_mean = df['Salary'].mean()
df['Salary_mean_imputed'] = df['Salary'].fillna(salary_mean)
print("\n平均値で補完したデータ:")
print(df)出力するとAge列のデータとSalary列のデータの欠損値にそれぞれの平均値で埋められたことが分かります。
中央値での補完
数値データの欠損値を中央値で埋めます。
import pandas as pd
# Age列の中央値で補完
age_median = df['Age'].median()
df['Age_median_imputed'] = df['Age'].fillna(age_median)
# Salary列の中央値で補完
salary_median = df['Salary'].median()
df['Salary_median_imputed'] = df['Salary'].fillna(salary_median)
print("\n中央値で補完したデータ:")
print(df)出力するとAge列のデータとSalary列のデータの欠損値にそれぞれの中央値で埋められたことが分かります。
最頻値(モード)での補完
カテゴリデータや数値データの欠損値を最頻値で埋めます。
import pandas as pd
# Gender列の最頻値で補完
gender_mode = df['Gender'].mode()[0]
df['Gender_mode_imputed'] = df['Gender'].fillna(gender_mode)
print("\n最頻値で補完したデータ:")
print(df)出力するとGender列のデータの欠損値にそれぞれの最頻値で埋められたことが分かります。
機械学習モデルを使った補完(KNN Imputer)
K近傍法(KNN)を用いて欠損値を補完します。これは、他の近傍データを基に欠損値を推定する方法です。
import pandas as pd
from sklearn.impute import KNNImputer
# 数値データのみにKNN Imputerを適用
imputer = KNNImputer(n_neighbors=2)
# 対象列を選択
numeric_cols = ['Age', 'Salary']
df_numeric = df[numeric_cols]
# 補完の実行
df_knn_imputed = imputer.fit_transform(df_numeric)
# DataFrameに戻す
df_knn_imputed = pd.DataFrame(df_knn_imputed, columns=['Age_knn_imputed', 'Salary_knn_imputed'])
# 元のDataFrameに追加
df = pd.concat([df, df_knn_imputed], axis=1)
print("\nKNN Imputerで補完したデータ:")
print(df)出力するとknn近傍法により欠損値を補完されたカラムが追加されます。
最後まで出力を終えると欠損値を補完した、平均値、中央値、最頻値、knn近傍法により追加した全てのカラムが追加されています。
それぞれの補完方法についての見解
欠損値を削除せずにデータを保持したい場合に有効です。平均値、中央値、最頻値の補完は簡単ですが、データの分布や特性を考慮する必要があります。機械学習モデルを用いた補完は、より精度の高い推定が可能ですが、計算コストが高くなる場合があります。
適切な欠損値処理を行うことで、データの品質を向上させ、機械学習モデルの性能を最大限に引き出すことができます。実際のデータ分析では、複数の補完方法を試し、モデルの性能を比較することが推奨されます。
最尤法による欠損値の補完
データ解析において、欠損値の処理は非常に重要なステップです。前回のセクションでは、基本的な欠損値の処理方法について学びましたが、今回は最尤法(Maximum Likelihood Estimation, MLE)を用いた欠損値の補完方法について詳しく説明します。最尤法は統計的に堅牢な手法であり、特に複雑なデータセットや多変量データにおいて効果的です。
最尤法(MLE)とは?
最尤法(MLE)は、与えられたデータが最も高い確率で観測されるようなモデルのパラメータを推定する統計手法です。欠損値の補完においては、データが特定の確率分布に従うと仮定し、その分布のパラメータを最尤法で推定して欠損値を補完します。
最尤法の基本的な流れ
- モデルの仮定:データが従う確率分布(例: 多変量正規分布)を仮定します。
- 尤度関数の構築:仮定した分布に基づき、観測データの尤度(確率)を計算します。
- パラメータの推定:尤度関数を最大化するパラメータを見つけます。
- 欠損値の補完:推定された分布を用いて、欠損値の条件付き期待値を計算し、補完します。
最尤法の数式
最尤法の核心は尤度関数(Likelihood Function)です。データがパラメータ $θ$ に依存する確率分布$f(x \mid \theta)$ に従うと仮定します。観測データ $X = { x_1, x_2, \dots, x_n }$ に対する尤度関数は以下のように定義されます。
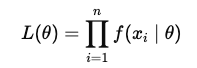
通常、対数尤度関数(Log-Likelihood Function)を用いて計算を簡略化します。
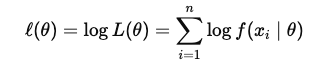
最尤推定量 $\hat{\theta}$ は、この対数尤度関数を最大化する ${\theta}$ の値です。
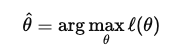
EMアルゴリズムと最尤法
欠損データが存在する場合、直接最尤推定を行うことは困難です。そこで、EMアルゴリズム(Expectation-Maximization Algorithm)が活用されます。EMアルゴリズムは欠損データを含むモデルのパラメータを最尤推定するための反復的な手法です。
EMアルゴリズムのステップ
- 初期化: パラメータ $\theta^{(0)}$ を初期値で設定します。
- Eステップ(Expectation Step):
- 現在のパラメータ $\theta^{(t)}$ を用いて、欠損データ $Z$ の条件付き期待値 $Q(\theta \mid \theta^{(t)}) = \mathbb{E}\left[\log L(\theta; X, Z) \mid X, \theta^{(t)} \right]$ を計算します。
- Mステップ(Maximization Step):
- $Q(\theta \mid \theta^{(t)})$ を最大化する新しいパラメータ $\theta^{(t+1)}$ を求めます。
- 収束判定: パラメータの変化が十分小さくなるまで、EステップとMステップを繰り返します。
EMアルゴリズムの数式
Eステップでは、現在のパラメータ $\theta^{(t)}$ を用いて、欠損データの条件付き期待値を計算します。
$$Q(\theta \mid \theta^{(t)}) = \mathbb{E}\left[\log L(\theta; X, Z) \mid X, \theta^{(t)} \right]$$
Mステップでは、上記の期待値を最大化する $\theta$ を求めます。
$$\theta^{(t+1)} = \arg \max_{\theta} Q(\theta \mid \theta^{(t)})$$
このプロセスを収束するまで繰り返すことで、最尤推定値 $\hat{\theta}$ を得ることができます。
Pythonでの実装方法
Pythonでは、scikit-learnのIterativeImputerやstatsmodelsのMICE(Multiple Imputation by Chained Equations)を使用して、最尤法に基づく欠損値の補完を実現できます。ここでは、scikit-learnのIterativeImputerを使用した例を紹介します。
IterativeImputerを用いた欠損値補完の実装例
以下のコードでは、IterativeImputerを使用して欠損値を補完します。この手法はEMアルゴリズムに類似したアプローチを採用しています。
import pandas as pd
import numpy as np
from sklearn.experimental import enable_iterative_imputer # noqa
from sklearn.impute import IterativeImputer
# データの読み込み
df = pd.read_csv('employee_data.csv')
print("元のデータ:")
print(df)
# 数値データのみを選択
numeric_df = df.select_dtypes(include=np.number)
# IterativeImputerの設定
imputer = IterativeImputer(random_state=0)
# 補完の実行
df_imputed = pd.DataFrame(imputer.fit_transform(numeric_df), columns=numeric_df.columns)
# 元のDataFrameに補完結果をマージ
df[numeric_df.columns] = df_imputed
print("\n補完後のデータ:")
print(df)出力:
元のデータ:
ID Name Age Gender Salary
0 1 田中太郎 28.0 男性 500000.0
1 2 鈴木花子 NaN 女性 600000.0
2 3 佐藤次郎 35.0 男性 NaN
3 4 高橋三郎 40.0 男性 700000.0
4 5 中村美咲 25.0 女性 450000.0
5 6 小林健 32.0 NaN 550000.0
6 7 山本久美 29.0 女性 480000.0
7 8 伊藤一郎 31.0 男性 620000.0
8 9 渡辺さおり NaN 女性 NaN
9 10 木村拓哉 38.0 男性 800000.0
補完後のデータ:
ID Name Age Gender Salary
0 1.0 田中太郎 28 男性 500000
1 2.0 鈴木花子 32 女性 600000
2 3.0 佐藤次郎 35 男性 587500
3 4.0 高橋三郎 40 男性 700000
4 5.0 中村美咲 25 女性 450000
5 6.0 小林健 32 NaN 550000
6 7.0 山本久美 29 女性 480000
7 8.0 伊藤一郎 31 男性 620000
8 9.0 渡辺さおり 32 女性 587500
9 10.0 木村拓哉 38 男性 800000IterativeImputer
IterativeImputerは、多変量回帰モデルを用いて欠損値を補完します。random_stateを設定することで再現性を確保しています。
MICEを用いた欠損値補完の実装例
IterativeImputerはEMアルゴリズムに類似した手法を使用していますが、ここではstatsmodelsのMICEを用いた例も紹介します。MICEはEMアルゴリズムとは厳密に言うと異なりますが、欠損データ補完の手法としては類似の目的を持つため、簡便な代替手法として利用できます。特に、MICEは欠損データの不確実性を考慮し、補完されたデータセットを使って分析を行うのに適しています。一方、EMアルゴリズムは、欠損値を扱いつつ、モデル全体のパラメータ推定に重点を置いています。
import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.imputation import mice
# データの読み込み
df = pd.read_csv('employee_data.csv')
print("元のデータ:")
print(df)
# 数値データのみを選択
numeric_df = df.select_dtypes(include=np.number)
# MICE(Multiple Imputation by Chained Equations)の設定
imp = mice.MICEData(numeric_df)
# 補完の実行
df_imputed = imp.data
# 元のDataFrameに補完結果をマージ
df[numeric_df.columns] = df_imputed
print("\n補完後のデータ:")
print(df)出力:
元のデータ:
ID Name Age Gender Salary
0 1 田中太郎 28.0 男性 500000.0
1 2 鈴木花子 NaN 女性 600000.0
2 3 佐藤次郎 35.0 男性 NaN
3 4 高橋三郎 40.0 男性 700000.0
4 5 中村美咲 25.0 女性 450000.0
5 6 小林健 32.0 NaN 550000.0
6 7 山本久美 29.0 女性 480000.0
7 8 伊藤一郎 31.0 男性 620000.0
8 9 渡辺さおり NaN 女性 NaN
9 10 木村拓哉 38.0 男性 800000.0
補完後のデータ:
ID Name Age Gender Salary
0 1 田中太郎 28.0 男性 500000.0
1 2 鈴木花子 32.0 女性 600000.0
2 3 佐藤次郎 35.0 男性 600000.0
3 4 高橋三郎 40.0 男性 700000.0
4 5 中村美咲 25.0 女性 450000.0
5 6 小林健 32.0 NaN 550000.0
6 7 山本久美 29.0 女性 480000.0
7 8 伊藤一郎 31.0 男性 620000.0
8 9 渡辺さおり 32.0 女性 600000.0
9 10 木村拓哉 38.0 男性 800000.0MICEData
statsmodelsのMICEDataを用いて、欠損値を含むデータの補完準備を行います。
最尤法の利点と欠点
| 利点 | 欠点 |
|---|---|
| 統計的妥当性: 最尤法は統計学的に理論的な基盤がしっかりしており、パラメータ推定において一貫性と効率性を持ちます。 | 計算コスト: 特に高次元データや複雑なモデルでは、計算が非常に重くなることがあります。 |
| 柔軟性: 様々な確率分布やモデルに適用可能であり、多様なデータに対応できます。 | モデル依存性: 仮定する確率分布が現実のデータと合致していない場合、補完結果が不正確になる可能性があります。 |
| データ利用効率: 欠損値がある場合でも、利用可能なデータ全体を活用してパラメータを推定します。 | 局所最適解: EMアルゴリズムなどの反復手法を用いる場合、初期値に依存して局所最適解に収束するリスクがあります。 |
| 欠損データの種類への依存: MNAR(Missing Not at Random)のような欠損データに対しては、最尤法が適切に機能しない場合があります。 |
MNARへのアプローチの選択
MNARへの対処は非常に困難であり、データの欠損メカニズムに強く依存します。最適な手法はデータの構造や欠損の理由に左右されるため、以下のようなステップを踏むのが理想です。
- 欠損パターンの理解:データがどのように欠損しているのか、MNARの可能性を評価する。
- 感度分析やシナリオ分析を通じて、欠損が分析にどの程度影響するかを確認。
- 高度なモデル(ベイズ推定、EMアルゴリズム)を活用し、欠損データの補完を行う。
- 多重代入法やパターンモデリングによって、欠損の不確実性を反映した推定を行う。
以上で欠損値の補完の説明は終わりです。MNARの対処法などはまた違う場所で行ってみたいと思っています。
カテゴリカル変数のエンコーディング
機械学習モデルは数値データを扱うため、カテゴリカルデータを数値に変換する必要があります。
エンコーディングの方法
ラベルエンコーディング
カテゴリを整数にマッピング。
例:{‘Male’: 0, ‘Female’: 1}
ワンホットエンコーディング
カテゴリごとに新しいバイナリ列を作成。
| Gender_Male | Gender_Female |
|---|---|
| 1 | 0 |
| 0 | 1 |
Pythonでの実装例
from sklearn.preprocessing import LabelEncoder
import pandas as pd
# データの読み込み
df = pd.read_csv('employee_data2.csv')
print("元のデータ:")
print(df)
# City列を文字列型に変換
df['City'] = df['City'].astype(str)
# ラベルエンコーディング
le = LabelEncoder()
df['Gender'] = le.fit_transform(df['Gender'])
# ワンホットエンコーディング
df = pd.get_dummies(df, columns=['City'], dtype=int) # dtype=int を追加
print("\nエンコーディング後のデータ:")
print(df) 出力:
元のデータ:
ID Name Gender Age City Salary
0 1 田中太郎 男性 28 Tokyo 500000
1 2 鈴木花子 女性 32 Osaka 600000
2 3 佐藤次郎 男性 35 Nagoya 450000
3 4 高橋三郎 男性 40 Tokyo 700000
4 5 中村美咲 女性 25 Kyoto 450000
エンコーディング後のデータ:
ID Name Gender Age Salary City_Kyoto City_Nagoya City_Osaka \
0 1 田中太郎 1 28 500000 0 0 0
1 2 鈴木花子 0 32 600000 0 0 1
2 3 佐藤次郎 1 35 450000 0 1 0
3 4 高橋三郎 1 40 700000 0 0 0
4 5 中村美咲 0 25 450000 1 0 0
City_Tokyo
0 1
1 0
2 0
3 1
4 0 高カーディナリティの処理(カテゴリの種類が多い場合)
カテゴリの種類が多い場合(高カーディナリティ)、次元の呪いに陥る可能性があります。この場合、頻度の低いカテゴリを「その他」にまとめるなどの対策が必要です。
特徴量のスケーリングと正規化
特徴量のスケーリングは、モデルの性能に大きな影響を与えます。
スケーリングの種類
標準化(Z-score正規化)
- 平均を0、標準偏差を1に調整。
$$z = \frac{(x – \mu)}{\sigma}$$
from sklearn.preprocessing import StandardScaler
# データの読み込み
df = pd.read_csv('employee_data2.csv')
print("元のデータ:")
print(df)
# 標準化
scaler = StandardScaler()
df[['Age', 'Salary']] = scaler.fit_transform(df[['Age', 'Salary']])
print("\標準化後のデータ:")
print(df)Min-Maxスケーリング
- データを0から1の範囲に変換。
$$x_{\text{scaled}} = \frac{x – x_{\text{min}}}{x_{\text{max}} – x_{\text{min}}}$$
from sklearn.preprocessing import MinMaxScaler
import pandas as pd
# データの読み込み
df = pd.read_csv('employee_data2.csv')
print("元のデータ:")
print(df)
# Min-Maxスケーリング
minmax_scaler = MinMaxScaler()
df[['Age', 'Salary']] = minmax_scaler.fit_transform(df[['Age', 'Salary']])
print("\nMin-Maxスケーリング後のデータ:")
print(df)スケーリングが必要な理由
- アルゴリズム(例:KNN、SVM)は、特徴量の尺度に敏感。
- スケーリングされていないと、一部の特徴量がモデルに過度な影響を与える。
外れ値の検出と処理
外れ値はモデルの性能を低下させる可能性があります。
外れ値の検出方法
箱ひげ図(ボックスプロット)
from sklearn.preprocessing import StandardScaler
import seaborn as sns
import pandas as pd
# データの読み込み
df = pd.read_csv('employee_data3.csv')
# 標準化
scaler = StandardScaler()
df[['Age', 'Salary']] = scaler.fit_transform(df[['Age', 'Salary']])
print("\標準化後のデータ:")
print(df)
sns.boxplot(x=df['Age'])出力:
\標準化後のデータ:
ID Name Gender Age City Salary
0 1 田中太郎 男性 -0.594502 Tokyo -0.604708
1 2 鈴木花子 女性 -0.439414 Osaka -0.086387
2 3 佐藤次郎 男性 -0.323099 Nagoya -0.863868
3 4 高橋三郎 男性 -0.129240 Tokyo 0.431934
4 5 中村美咲 女性 -0.710817 Kyoto -0.863868
5 6 外れ値さん 男性 2.197072 Tokyo 1.986897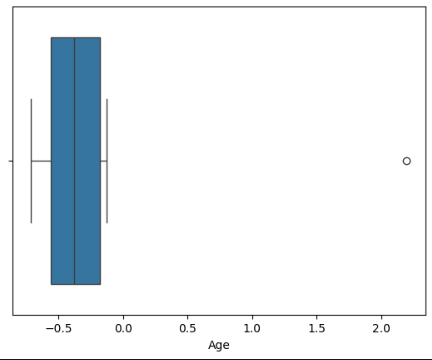
統計的手法
- Zスコア:絶対値が3を超えるものを外れ値とする。
IQR(四分位範囲)
$$\text{IQR} = Q_3 – Q_1$$
外れ値の境界
$$\text{下限} = Q_1 – 1.5 \times \text{IQR}$$
$$\text{上限} = Q_3 + 1.5 \times \text{IQR}$$
IQRを使った例:
Q1 = df['Age'].quantile(0.25)
Q3 = df['Age'].quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
# 外れ値の検出
outliers = df[(df['Age'] < lower_bound) | (df['Age'] > upper_bound)]
print(outliers)外れ値の処理方法
削除
外れ値を削除。
import pandas as pd
# データの読み込み
df = pd.read_csv('employee_data3.csv')
print("元のデータ:")
print(df)
# 外れ値の検出
Q1 = df['Age'].quantile(0.25)
Q3 = df['Age'].quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
outliers = df[(df['Age'] < lower_bound) | (df['Age'] > upper_bound)]
# 外れ値の削除
df_no_outliers = df[~((df['Age'] < lower_bound) | (df['Age'] > upper_bound))]
print("外れ値を削除したデータ:")
print(df_no_outliers) 出力:
外れ値が削除されています。
元のデータ:
ID Name Gender Age City Salary
0 1 田中太郎 男性 28 Tokyo 500000
1 2 鈴木花子 女性 32 Osaka 600000
2 3 佐藤次郎 男性 35 Nagoya 450000
3 4 高橋三郎 男性 40 Tokyo 700000
4 5 中村美咲 女性 25 Kyoto 450000
5 6 外れ値さん 男性 100 Tokyo 1000000
外れ値を削除したデータ:
ID Name Gender Age City Salary
0 1 田中太郎 男性 28 Tokyo 500000
1 2 鈴木花子 女性 32 Osaka 600000
2 3 佐藤次郎 男性 35 Nagoya 450000
3 4 高橋三郎 男性 40 Tokyo 700000
4 5 中村美咲 女性 25 Kyoto 450000置換
上限・下限値に置き換える(キャッピング)。
import pandas as pd
# データの読み込み
df = pd.read_csv('employee_data3.csv')
print("元のデータ:")
print(df)
# 外れ値の検出
Q1 = df['Age'].quantile(0.25)
Q3 = df['Age'].quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
# 外れ値の上限・下限値に置き換え
df['Age'] = df['Age'].clip(lower=lower_bound, upper=upper_bound)
print("外れ値を上限・下限値に置き換えたデータ:")
print(df)出力:
外れ値が上限値に置き換えられています。
元のデータ:
ID Name Gender Age City Salary
0 1 田中太郎 男性 28 Tokyo 500000
1 2 鈴木花子 女性 32 Osaka 600000
2 3 佐藤次郎 男性 35 Nagoya 450000
3 4 高橋三郎 男性 40 Tokyo 700000
4 5 中村美咲 女性 25 Kyoto 450000
5 6 外れ値さん 男性 100 Tokyo 1000000
外れ値を上限・下限値に置き換えたデータ:
ID Name Gender Age City Salary
0 1 田中太郎 男性 28.000 Tokyo 500000
1 2 鈴木花子 女性 32.000 Osaka 600000
2 3 佐藤次郎 男性 35.000 Nagoya 450000
3 4 高橋三郎 男性 40.000 Tokyo 700000
4 5 中村美咲 女性 25.000 Kyoto 450000
5 6 外れ値さん 男性 53.375 Tokyo 1000000変換
対数変換や平方根変換でデータの分布を調整。
import pandas as pd
import numpy as np
# データの読み込み
df = pd.read_csv('employee_data3.csv')
print("元のデータ:")
print(df)
# 対数変換
df['Age'] = np.log(df['Age'])
print("対数変換後のデータ:")
print(df)出力:
このデータの年齢の列に対して対数変換を行うと、分布が正規分布に近づき、平均値や標準偏差などの統計量をより適切に計算できるようになります。また、外れ値の影響も抑制されるため、分析結果の解釈が容易になります。
元のデータ:
ID Name Gender Age City Salary
0 1 田中太郎 男性 28 Tokyo 500000
1 2 鈴木花子 女性 32 Osaka 600000
2 3 佐藤次郎 男性 35 Nagoya 450000
3 4 高橋三郎 男性 40 Tokyo 700000
4 5 中村美咲 女性 25 Kyoto 450000
5 6 外れ値さん 男性 100 Tokyo 1000000
対数変換後のデータ:
ID Name Gender Age City Salary
0 1 田中太郎 男性 3.332205 Tokyo 500000
1 2 鈴木花子 女性 3.465736 Osaka 600000
2 3 佐藤次郎 男性 3.555348 Nagoya 450000
3 4 高橋三郎 男性 3.688879 Tokyo 700000
4 5 中村美咲 女性 3.218876 Kyoto 450000
5 6 外れ値さん 男性 4.605170 Tokyo 1000000外れ値の検出には統計的な指標が不可欠です。平均値や標準偏差、四分位数を理解することで、データのばらつきを正確に評価できます。
探索的データ解析(EDA)と可視化
EDAはデータの理解を深めるためのプロセスであり、可視化はその中心的な手法です。
主な可視化手法
- ヒストグラム:データの分布を視覚化。
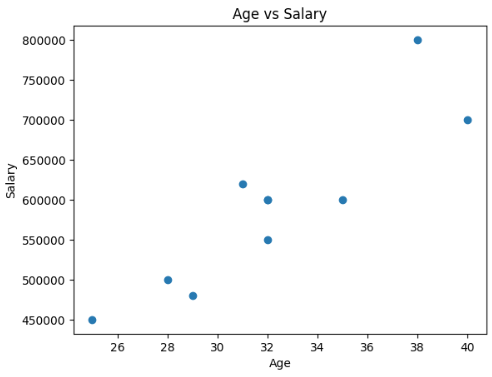
- 散布図:二変数間の関係を表示。
- ボックスプロット:分布の要約と外れ値の検出。
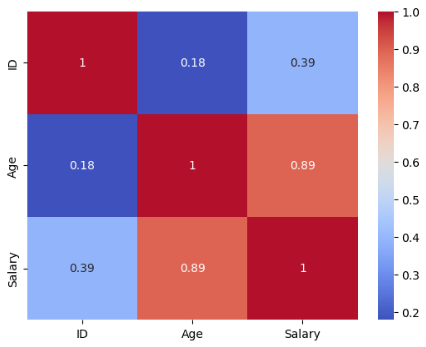
- ヒートマップ:相関行列の可視化。
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
# データの読み込み
df = pd.read_csv('employee_data4.csv')
print("元のデータ:")
print(df)
# 数値データのみを含むDataFrameを作成
numeric_df = df.select_dtypes(include=['number'])
# ヒストグラム
plt.hist(numeric_df['Age'], bins=20)
plt.xlabel('Age')
plt.ylabel('Frequency')
plt.title('Age Distribution')
plt.show()
# 散布図
plt.scatter(df['Age'], numeric_df['Salary'])
plt.xlabel('Age')
plt.ylabel('Salary')
plt.title('Age vs Salary')
plt.show()
# 相関行列ヒートマップ
corr = numeric_df.corr()
sns.heatmap(corr, annot=True, cmap='coolwarm')
plt.show()出力:
元のデータ:
ID Name Age Gender Salary
0 1 田中太郎 28.0 男性 500000.0
1 2 鈴木花子 32.0 女性 600000.0
2 3 佐藤次郎 35.0 男性 600000.0
3 4 高橋三郎 40.0 男性 700000.0
4 5 中村美咲 25.0 女性 450000.0
5 6 小林健 32.0 NaN 550000.0
6 7 山本久美 29.0 女性 480000.0
7 8 伊藤一郎 31.0 男性 620000.0
8 9 渡辺さおり 32.0 女性 600000.0
9 10 木村拓哉 38.0 男性 800000.0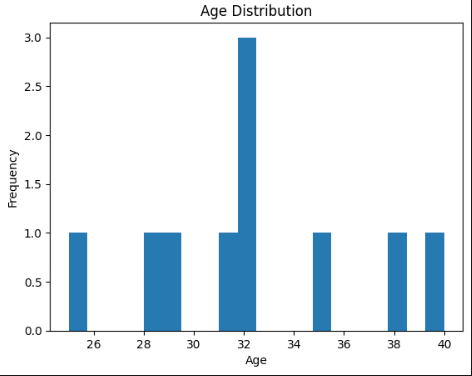
相関の分析
特徴量間の相関を理解することで、モデルの性能を最適化できます。
通常の相関係数
import pandas as pd
# データの読み込み
df = pd.read_csv('employee_data5.csv')
print("元のデータ:")
print(df)
# 数値データのみを含むDataFrameを作成
numeric_df = df.select_dtypes(include=['number'])
# 相関行列の計算
corr_matrix = numeric_df.corr()
print(corr_matrix)
# 特定のターゲット変数との相関
print(numeric_df.corr()['Salary'].sort_values(ascending=False)) 出力:
データ間の関係性を数値化することで、重要な特徴量を特定し、不要な特徴量を削減できます。
元のデータ:
ID Name Gender Age Salary Experience Bonus
0 1 田中太郎 男性 28 500000 2 5000
1 2 鈴木花子 女性 32 600000 5 6000
2 3 佐藤次郎 男性 35 600000 3 7000
3 4 高橋三郎 男性 40 700000 10 8000
4 5 中村美咲 女性 25 450000 1 4500
5 6 小林健 男性 32 550000 4 3000
6 7 山本久美 女性 29 480000 2 4000
7 8 伊藤一郎 男性 31 620000 7 6500
8 9 渡辺さおり 女性 32 600000 6 6200
9 10 木村拓哉 男性 38 800000 8 8500
ID Age Salary Experience Bonus
ID 1.000000 0.178755 0.392295 0.374941 0.177015
Age 0.178755 1.000000 0.894561 0.832759 0.761945
Salary 0.392295 0.894561 1.000000 0.877601 0.854745
Experience 0.374941 0.832759 0.877601 1.000000 0.743897
Bonus 0.177015 0.761945 0.854745 0.743897 1.000000
Salary 1.000000
Age 0.894561
Experience 0.877601
Bonus 0.854745
ID 0.392295
Name: Salary, dtype: float64ID以外の全ての特徴量に相関関係があることが分かります。
相関係数の種類
データの相関を理解することは、特徴量間の関係性を把握し、モデルの性能を向上させるために重要です。ここでは、ピアソンの相関係数とスピアマンの順位相関係数について説明します。
- ピアソンの相関係数:線形関係を測定。
- スピアマンの順位相関係数:単調関係を測定。
ピアソンの相関係数
ピアソンの相関係数は、線形関係を測定します。値は-1から1の範囲を取り、1は完全な正の線形関係、-1は完全な負の線形関係、0は線形関係がないことを示します。
$$r = \frac{\sum (x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum (x_i – \bar{x})^2} \sqrt{\sum (y_i – \bar{y})^2}}$$
スピアマンの順位相関係数
スピアマンの順位相関係数は、単調関係を測定します。これは、データが必ずしも線形ではなくても、一方が増加すればもう一方も増加(または減少)する関係を評価します。スピアマンの相関係数も-1から1の範囲を取り、1は完全な単調増加関係、-1は完全な単調減少関係、0は単調関係がないことを示します。
$$\rho = 1 – \frac{6 \sum d_i^2}{n(n^2 – 1)}$$
ここで、$di$ は各ペアの順位の差、$n$ はデータポイントの数です。
スピアマンの順位相関係数の利用場面
- データが線形ではないが、単調な関係が存在する場合。
- 順位データや順序が重要な場合。
- 外れ値に敏感でない関係性の評価が必要な場合。
それぞれの相関分析のコーディング例
import pandas as pd
import numpy as np
from scipy.stats import pearsonr, spearmanr
# データの読み込み
df = pd.read_csv('employee_data5.csv')
print("元のデータ:")
print(df)
# 数値データのみを含むDataFrameを作成
numeric_df = df.select_dtypes(include=['number'])
# ピアソンの相関係数の計算
pearson_corr, pearson_p = pearsonr(numeric_df['Age'], numeric_df['Salary'])
print(f"ピアソンの相関係数: {pearson_corr:.4f}, p値: {pearson_p:.4f}")
# ヒートマップで可視化
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.show()
# スピアマンの順位相関係数の計算
spearman_corr, spearman_p = spearmanr(numeric_df['Age'], numeric_df['Salary'])
print(f"スピアマンの順位相関係数: {spearman_corr:.4f}, p値: {spearman_p:.4f}")
# ヒートマップで可視化
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.show() 出力:
元のデータ:
ID Name Gender Age Salary Experience Bonus
0 1 田中太郎 男性 28 500000 2 5000
1 2 鈴木花子 女性 32 600000 5 6000
2 3 佐藤次郎 男性 35 600000 3 7000
3 4 高橋三郎 男性 40 700000 10 8000
4 5 中村美咲 女性 25 450000 1 4500
5 6 小林健 男性 32 550000 4 3000
6 7 山本久美 女性 29 480000 2 4000
7 8 伊藤一郎 男性 31 620000 7 6500
8 9 渡辺さおり 女性 32 600000 6 6200
9 10 木村拓哉 男性 38 800000 8 8500ピアソンの相関係数: 0.8946, p値: 0.0005
相関分析の結果からピアソンの相関係数が0.8946と非常に高く、p値が0.0005であることから、強い正の線形関係が存在することがわかります。
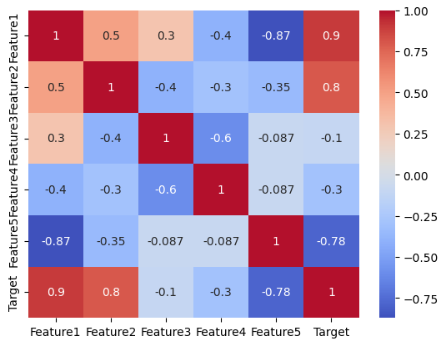
スピアマンの順位相関係数: 0.8261, p値: 0.0032
相関分析の結果から、スピアマンの相関係数が0.8261と高く、p値が0.0001であることから、強い正の単調関係が存在することがわかります。
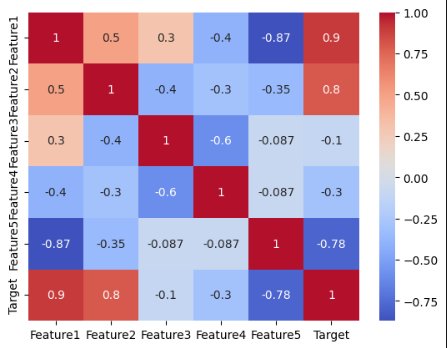
特徴量エンジニアリング
特徴量エンジニアリングは、モデルの性能を向上させるための新しい特徴量を生成するプロセスです。
手法
- 特徴量の生成:既存のデータから新たな特徴量を作成。
- 例:日付データから年、月、日を抽出。
- 特徴量の分割:連続値をカテゴリに変換(ビニング)。
- 特徴量の組み合わせ:複数の特徴量を組み合わせる。
import pandas as pd
# データの読み込み
df = pd.read_csv('employee_data5.csv')
print("元のデータ:")
print(df)
# ビニング
df['Age_Group'] = pd.cut(df['Age'], bins=[0, 18, 35, 50, 100], labels=['Child', 'Youth', 'Adult', 'Senior'])
# 特徴量の組み合わせ
df['Salary_Experience_Ratio'] = df['Salary'] / df['Experience']
print("\n特徴量エンジニアリング後のデータ:")
print(df)出力:
元のデータ:
ID Name Gender Age Salary Experience Bonus
0 1 田中太郎 男性 28 500000 2 5000
1 2 鈴木花子 女性 32 600000 5 6000
2 3 佐藤次郎 男性 35 600000 3 7000
3 4 高橋三郎 男性 40 700000 10 8000
4 5 中村美咲 女性 25 450000 1 4500
5 6 小林健 男性 32 550000 4 3000
6 7 山本久美 女性 29 480000 2 4000
7 8 伊藤一郎 男性 31 620000 7 6500
8 9 渡辺さおり 女性 32 600000 6 6200
9 10 木村拓哉 男性 38 800000 8 8500
特徴量エンジニアリング後のデータ:
ID Name Gender Age Salary Experience Bonus Age_Group \
0 1 田中太郎 男性 28 500000 2 5000 Youth
1 2 鈴木花子 女性 32 600000 5 6000 Youth
2 3 佐藤次郎 男性 35 600000 3 7000 Youth
3 4 高橋三郎 男性 40 700000 10 8000 Adult
4 5 中村美咲 女性 25 450000 1 4500 Youth
5 6 小林健 男性 32 550000 4 3000 Youth
6 7 山本久美 女性 29 480000 2 4000 Youth
7 8 伊藤一郎 男性 31 620000 7 6500 Youth
8 9 渡辺さおり 女性 32 600000 6 6200 Youth
9 10 木村拓哉 男性 38 800000 8 8500 Adult
Salary_Experience_Ratio
0 250000.000000
1 120000.000000
2 200000.000000
3 70000.000000
4 450000.000000
5 137500.000000
6 240000.000000
7 88571.428571
8 100000.000000
9 100000.000000 データのバランシング手法
不均衡データは、特に分類問題においてモデルの性能を著しく低下させる要因となります。例えば、少数クラスのデータが十分に学習されないことで、モデルは多数クラスに偏った予測を行いやすくなります。これを防ぐために、データのバランシング手法を適用することが重要です。
今回は不均衡データを実際に作ってみてからデータのバランシング手法を行います。
手法の手順
- オーバーサンプリング:
- 少数クラスのデータを増やす。
- SMOTE(Synthetic Minority Over-sampling Technique)が一般的。
- アンダーサンプリング:
- 多数クラスのデータを減らす。
- 組み合わせ:
- オーバーサンプリングとアンダーサンプリングの併用。
不均衡データの作成方法
CSVデータの作成
from sklearn.datasets import make_classification
import pandas as pd
# 不均衡な分類データの生成
X, y = make_classification(n_samples=1000, # サンプル数
n_features=5, # 特徴量の数
n_informative=3, # 有益な特徴量の数
n_redundant=1, # 冗長な特徴量の数
n_clusters_per_class=1,
weights=[0.9, 0.1], # クラスの不均衡比率
flip_y=0, # ラベルノイズ
random_state=42)
# データフレームの作成
df = pd.DataFrame(X, columns=['Feature1', 'Feature2', 'Feature3', 'Feature4', 'Feature5'])
df['Target'] = y
# CSVファイルとして保存
df.to_csv('imbalanced_data.csv', index=False)
print("サンプルデータが 'imbalanced_data.csv' として保存されました。")
手法
オーバーサンプリング
オーバーサンプリングは、少数クラスのデータを人工的に増やす手法です。これにより、クラス間のバランスを改善し、モデルが少数クラスの特徴をよりよく学習できるようになります。
- SMOTE(Synthetic Minority Over-sampling Technique)
SMOTEは、少数クラスのデータポイント間で新しい合成サンプルを生成する手法です。具体的には、各少数クラスのサンプルに対して近傍のサンプルを選び、その間に線形補間を行うことで新たなデータを作成します。これにより、単純な複製によるオーバーフィッティングを防ぎつつ、データの多様性を保つことができます。
pip install imblearnfrom imblearn.over_sampling import SMOTE
import pandas as pd
df = pd.read_csv('imbalanced_data.csv')
# 特徴量とターゲットの分離
X = df.drop('Target', axis=1)
y = df['Target']
# SMOTEによるオーバーサンプリング
sm = SMOTE(random_state=42)
X_res, y_res = sm.fit_resample(X, y)
print("オリジナルデータセットのクラス分布:", y.value_counts())
print("リサンプリング後のクラス分布:", y_res.value_counts())出力:
不均衡データがオーバーサンプリングされ、均一になりました。
オリジナルデータセットのクラス分布: Target
0 900
1 100
Name: count, dtype: int64
リサンプリング後のクラス分布: Target
0 900
1 900
Name: count, dtype: int64アンダーサンプリング
アンダーサンプリングは、多数クラスのデータを減らす手法です。これにより、データセット全体のバランスを取ることができます。ただし、多数クラスの情報が減少するため、重要なパターンが失われるリスクがあります。
- ランダムアンダーサンプリング
多数クラスからランダムにサンプルを削減するシンプルな方法です。
from imblearn.under_sampling import RandomUnderSampler
import pandas as pd
df = pd.read_csv('imbalanced_data.csv')
# 特徴量とターゲットの分離
X = df.drop('Target', axis=1)
y = df['Target']
rus = RandomUnderSampler(random_state=42)
X_res, y_res = rus.fit_resample(X, y)
print("オリジナルデータセットのクラス分布:", y.value_counts())
print("アンダーサンプリング後のクラス分布:", y_res.value_counts())出力:
不均衡データがアンダーサンプリングされ、均一になりました。
オリジナルデータセットのクラス分布: Target
0 900
1 100
Name: count, dtype: int64
アンダーサンプリング後のクラス分布: Target
0 100
1 100
Name: count, dtype: int64組み合わせ
オーバーサンプリングとアンダーサンプリングを組み合わせることで、両方の手法の利点を活かしつつ、欠点を補完することができます。例えば、まずアンダーサンプリングで多数クラスを適度に減らし、その後SMOTEで少数クラスを増やす方法があります。
- SMOTE + Tomekリンク
SMOTEでオーバーサンプリングした後、Tomekリンクを用いてデータのノイズを削除する方法です。
from imblearn.combine import SMOTETomek
import pandas as pd
df = pd.read_csv('imbalanced_data.csv')
# 特徴量とターゲットの分離
X = df.drop('Target', axis=1)
y = df['Target']
smt = SMOTETomek(random_state=42)
X_res, y_res = smt.fit_resample(X, y)
print("組み合わせ後のクラス分布:", y_res.value_counts())出力:
不均衡データをSMOTEでオーバーサンプリングした後、Tomekリンクを用いてデータのノイズを削除しています。
組み合わせ後のクラス分布: Target
0 899
1 899
Name: count, dtype: int64その他の手法
- ADASYN(Adaptive Synthetic Sampling)
ADASYNはSMOTEの拡張で、難易度の高いサンプル周辺により多くの合成サンプルを生成します。これにより、モデルが境界付近のクラスをより正確に学習できるようになります。
from imblearn.over_sampling import ADASYN
import pandas as pd
df = pd.read_csv('imbalanced_data.csv')
# 特徴量とターゲットの分離
X = df.drop('Target', axis=1)
y = df['Target']
ada = ADASYN(random_state=42)
X_res, y_res = ada.fit_resample(X, y)
print("ADASYN後のクラス分布:", y_res.value_counts())出力:
ADASYN後のクラス分布: Target
0 900
1 894
Name: count, dtype: int64- 機械学習を使ったクラスの重み調整
データのバランスを調整する代わりに、モデルの学習時にクラスの重みを変更する方法です。これにより、少数クラスの誤分類に対するペナルティを増やし、バランスの取れた予測を促します。
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import pandas as pd
df = pd.read_csv('imbalanced_data.csv')
# 特徴量とターゲットの分離
X = df.drop('Target', axis=1)
y = df['Target']
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)
# SMOTEによるオーバーサンプリング
sm = SMOTE(random_state=42)
X_res_smote, y_res_smote = sm.fit_resample(X_train, y_train)
print("SMOTE後のクラス分布:\n", pd.Series(y_res_smote).value_counts())
# モデルの訓練と評価(例としてSMOTE後のデータを使用)
model = RandomForestClassifier(class_weight='balanced', random_state=42)
model.fit(X_res_smote, y_res_smote)
y_pred = model.predict(X_test)
# 評価結果の表示
print("分類レポート:\n", classification_report(y_test, y_pred))出力:
これは機械学習のランダムフォレストのアルゴリズムを使ったクラスの重み調整の例です。
SMOTE後のクラス分布:
Target
0 720
1 720
Name: count, dtype: int64
分類レポート:
precision recall f1-score support
0 0.99 0.97 0.98 180
1 0.76 0.95 0.84 20
accuracy 0.96 200
macro avg 0.88 0.96 0.91 200
weighted avg 0.97 0.96 0.97 200バランシング手法の選択ポイント
- データの特性
データセットのサイズやクラスの不均衡の程度に応じて、適切な手法を選択します。小規模なデータセットではアンダーサンプリングが有効な場合がありますが、大規模なデータセットではオーバーサンプリングが適しています。 - モデルの種類
一部のモデルはクラス不均衡に対して敏感であり、バランシング手法の適用が特に有効です。例えば、決定木ベースのモデルやニューラルネットワークなどです。 - 計算コスト
オーバーサンプリングはデータ量を増やすため、計算コストが上がる可能性があります。一方、アンダーサンプリングはデータ量を減らすため、計算コストを抑えることができます。
データのバランシングは、モデルの性能向上に直結する重要な前処理ステップです。適切な手法を選び、実装することで、より精度の高い予測モデルを構築することが可能になります。
重要なポイント
データ前処理と可視化は、モデルの性能を最大限に引き出すための基盤です。
データ前処理と可視化の主要なポイント
| 主要なポイント | 説明 |
|---|---|
| 欠損値の処理 | データの完全性を確保。 |
| カテゴリカルデータのエンコーディング(One-Hot-encoding) | モデルが理解可能な形式に変換。 |
| 特徴量のスケーリング | モデルの収束を速め、異なるスケールの特徴量が同等に扱われるようにする。 |
| 外れ値の処理 | データのばらつきを正確に反映。 |
| EDAと可視化 | データの深い理解。 |
| 相関分析 | 重要な特徴量の特定と冗長性の削減。 |
| 特徴量エンジニアリング | データから新しい特徴を作成し、モデルの性能向上や分析の理解を深める。 |
| データのバランシング | クラス不均衡の是正。 |
実践例:タイタニックデータセットの前処理ウォークスルー
ここでは、Kaggleで有名なタイタニックデータセットを用いて、最尤法による欠損値の補完を実践的に行います。具体的には、scikit-learnのIterativeImputerを使用し、補完後に相関分析と視覚的な検証を行います。また、箱ひげ図からの視覚的な観察に基づく結論の注意点や、生存率に影響を与える他の要因(性別、乗客クラス、搭乗場所など)についても考慮します。
データの読み込み
まず、タイタニックデータセットを読み込みます。Kaggleからダウンロードしたtrain.csvを使用します。
import pandas as pd
train = pd.read_csv('train.csv')
print("元のデータ:")
print(train.head())欠損値の確認
データセット内の欠損値を確認します。
# 欠損値の確認
print("\n欠損値の数:")
print(train.isnull().sum())出力:
欠損値の数:
PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 177
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64必要な前処理
今回はAgeに欠損値が多く含まれているため、最尤法を用いて補完します。補完対象の数値列として、Age、Fare、SibSp、Parchを選択します。
from sklearn.experimental import enable_iterative_imputer # noqa
from sklearn.impute import IterativeImputer
# 補完対象の数値列を指定
numeric_cols = ['Age', 'Fare', 'SibSp', 'Parch']
df_numeric = train[numeric_cols]
# IterativeImputerの設定
imputer = IterativeImputer(random_state=0)
# 補完の実行
df_imputed = pd.DataFrame(imputer.fit_transform(df_numeric), columns=numeric_cols)
# 補完後のデータを元のDataFrameに上書き
train[numeric_cols] = df_imputed
print("\n補完後のデータ:")
print(train[numeric_cols])出力:
補完後のデータ:
Age Fare SibSp Parch
0 22.00000 7.2500 1.0 0.0
1 38.00000 71.2833 1.0 0.0
2 26.00000 7.9250 0.0 0.0
3 35.00000 53.1000 1.0 0.0
4 35.00000 8.0500 0.0 0.0
.. ... ... ... ...
886 27.00000 13.0000 0.0 0.0
887 19.00000 30.0000 0.0 0.0
888 24.17135 23.4500 1.0 2.0
889 26.00000 30.0000 0.0 0.0
890 32.00000 7.7500 0.0 0.0特徴量のスケーリング
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
train[['Age', 'Fare']] = scaler.fit_transform(train[['Age', 'Fare']])補完結果の確認
補完後のデータに欠損値が存在しないことを確認します。
# 補完後の欠損値の確認
print("\n補完後の欠損値の数:")
print(train.isnull().sum())出力:
補完後の欠損値の数:
PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 0
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 687
Embarked 2
dtype: int64相関の分析
補完後のデータを用いて、AgeとFareの相関を分析します。ここでは、ピアソンの相関係数とスピアマンの順位相関係数を計算し、両者の関係性を評価します。
from scipy.stats import pearsonr, spearmanr
# 相関分析の対象列
corr_cols = ['Age', 'Fare']
# ピアソンの相関係数の計算
pearson_corr, pearson_p = pearsonr(train['Age'], train['Fare'])
print(f"ピアソンの相関係数: {pearson_corr:.4f}, p値: {pearson_p:.4f}")
# スピアマンの順位相関係数の計算
spearman_corr, spearman_p = spearmanr(train['Age'], train['Fare'])
print(f"スピアマンの順位相関係数: {spearman_corr:.4f}, p値: {spearman_p:.4f}")出力:
ピアソンの相関係数: 0.0784, p値: 0.0192
スピアマンの順位相関係数: 0.0929, p値: 0.0055視覚的な検証と考慮事項
箱ひげ図による視覚的な観察
AgeとSurvivedの関係を箱ひげ図で視覚化し、年齢が生存率にどのように影響しているかを観察します。
import matplotlib.pyplot as plt
import seaborn as sns
# 生存者と非生存者の年齢分布を箱ひげ図で表示
plt.figure(figsize=(10,5))
sns.boxplot(x='Survived', y='Age', data=train)
plt.title('Age Distribution by Survival Status')
plt.xlabel('Survived')
plt.ylabel('Age')
plt.xticks([0,1], ['No', 'Yes'])
plt.show()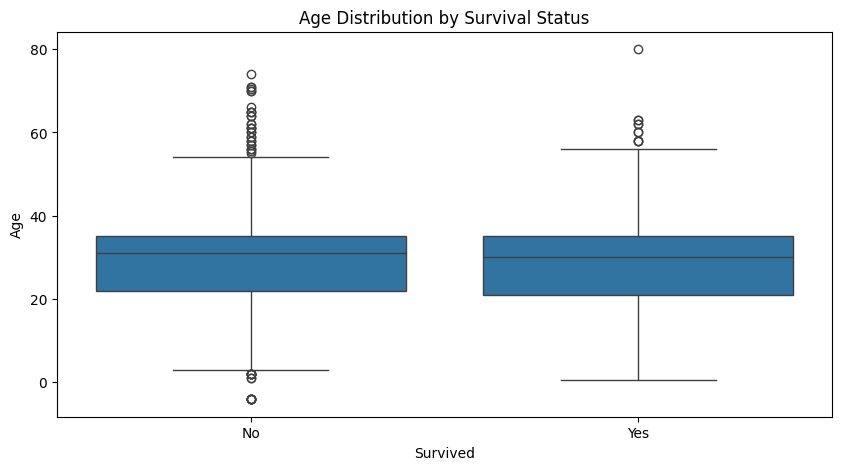
考慮事項
- 視覚的な観察の限界:
- この結論は、箱ひげ図から得られた視覚的な観察に基づいています。視覚的なパターンは有用ですが、統計的な検定を行うことで、観察された関係が偶然ではないことを確認する必要があります。例えば、T検定や分散分析(ANOVA)を用いて、年齢が生存に統計的に有意な影響を与えているかを検証できます。
- 他の要因の考慮:
- 生存率に影響を与える可能性のある他の要因(例えば、性別、乗客クラス、搭乗場所など)も考慮する必要があります。これらの要因を同時に分析することで、より包括的な理解が得られます。以下に、性別や乗客クラスを含めた相関分析と視覚化の例を示します。
他の要因の影響分析
Sex、Pclass、EmbarkedとSurvivedとの関係を分析し、生存率にどのような影響を与えているかを調べます。
性別と生存率
性別が生存率に与える影響を視覚化します。
# 性別と生存率の関係をカウントプロットで表示
plt.figure(figsize=(10,5))
sns.countplot(x='Sex', hue='Survived', data=train)
plt.title('Survival Count by Sex')
plt.xlabel('Sex')
plt.ylabel('Count')
plt.legend(['No', 'Yes'])
plt.show()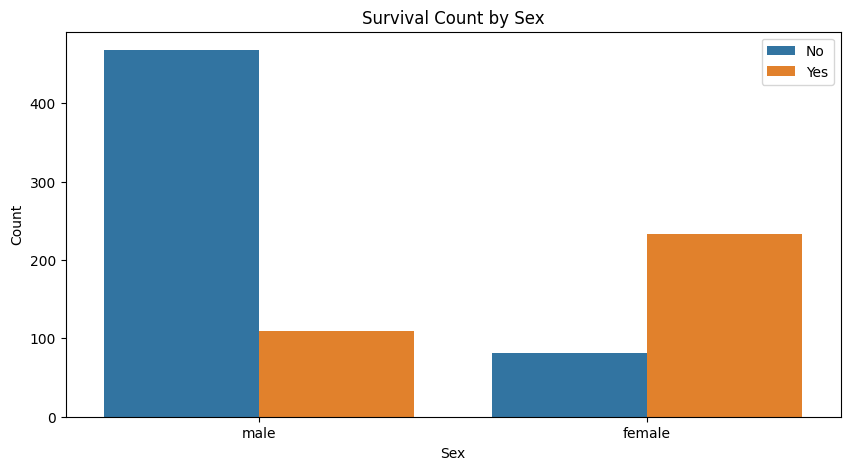
分析結果:
- 女性の生存率が高いことが視覚的に確認できます。これは歴史的なタイタニック事故のデータからも知られている事実です。
乗客クラスと生存率
乗客クラス(Pclass)が生存率に与える影響を視覚化します。
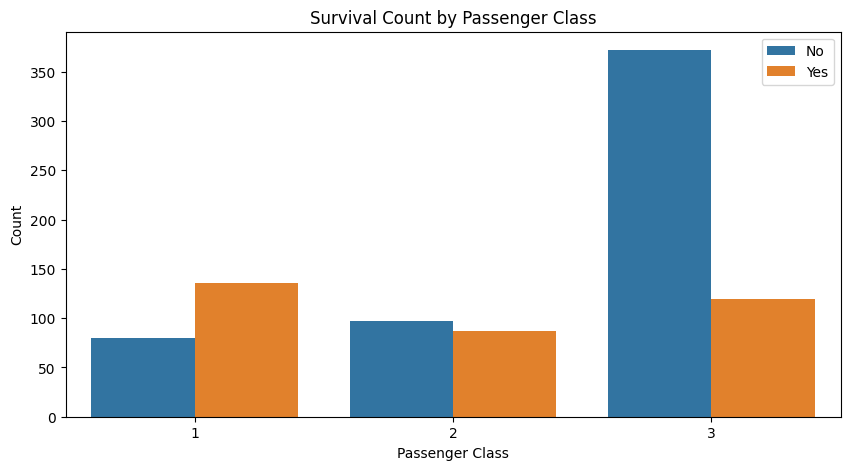
分析結果:
- 1等クラスの乗客の生存率が最も高く、3等クラスの生存率が最も低いことがわかります。これは、1等クラスの乗客が船の前方に位置していたため、救命ボートへのアクセスが容易だったことに起因しています。
搭乗場所と生存率
搭乗場所(Embarked)が生存率に与える影響を視覚化します。
# 搭乗場所と生存率の関係をカウントプロットで表示
plt.figure(figsize=(10,5))
sns.countplot(x='Embarked', hue='Survived', data=train)
plt.title('Survival Count by Embarked')
plt.xlabel('Embarked')
plt.ylabel('Count')
plt.legend(['No', 'Yes'])
plt.show()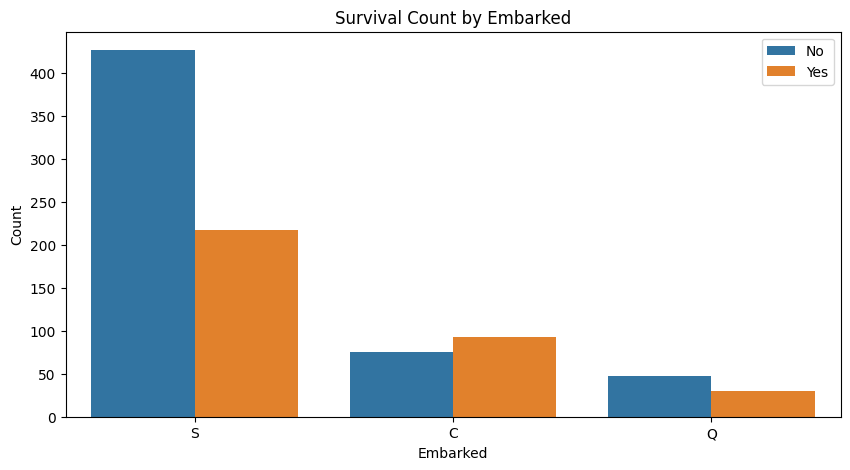
分析結果:
- サウサンプトン(S)から搭乗した乗客の生存率が他の港からの乗客よりも低い傾向が見られます。これは、サウサンプトンから乗船した乗客が多数を占めるため、他の港からの乗客との比較で生存率が相対的に低く見える可能性があります。
統計的検定の実施
視覚的な観察だけでなく、統計的な検定を行うことで、各要因が生存率に与える影響の有意性を確認します。
性別と生存率の関係(カイ二乗検定)
from scipy.stats import chi2_contingency
# 性別と生存率のクロス集計
contingency = pd.crosstab(train['Sex'], train['Survived'])
# カイ二乗検定の実行
chi2, p, dof, expected = chi2_contingency(contingency)
print(f"カイ二乗統計量: {chi2:.4f}, p値: {p:.4f}")出力:
カイ二乗統計量: 260.7170, p値: 0.0000解釈:
- p値が0.0000であり、有意水準5%で帰無仮説を棄却します。つまり、性別と生存率には統計的に有意な関連があることが示されます。
カイ二乗検定とは?
カイ二乗検定(Chi-squared test)は、観測データが期待される分布とどれほど一致しているかを評価するための統計的手法です。主にカテゴリーデータに対して使用され、以下の2つの主なタイプがあります。
適合度検定(Goodness-of-fit test):
観測データが特定の理論的分布に従っているかどうかを検定します。
独立性検定(Test of independence):
2つのカテゴリ変数の間に関連性があるかどうかを検定します。
$$\chi^2 = \sum \frac{(O_i – E_i)^2}{E_i}$$
| $χ2$ | カイ二乗統計量 |
| $Oi$ | 各カテゴリにおける観測頻度(実際のデータの値) |
| $Ei$ | 各カテゴリにおける期待頻度(理論的に予測された値) |
| $i$ | カテゴリのインデックス |
カイ二乗統計量は、各カテゴリにおける観測値と期待値の差の平方を期待値で割り、その合計を求めます。この計算により、観測データが期待分布からどれだけ離れているかを定量的に示します。
カイ二乗分布の特徴
- 自由度(Degrees of Freedom): カイ二乗分布は自由度によって形状が決まります。自由度は、データの中で独立して変化できるパラメータの数を示します。自由度が増加するにつれて、カイ二乗分布の形は正規分布に近づきます。
- 非対称性: カイ二乗分布は非対称で、右に尾を引く形をしています。自由度が少ないときは、特に尖った形をしており、自由度が大きくなるにつれて平坦になります。
- 0以上の値: カイ二乗分布は0以上の値のみを取るため、負の値は存在しません。これは、カイ二乗統計量が観測値と期待値の差の平方の和であるためです。
使用される場面
- 適合度検定(Goodness-of-Fit Test): 観測データが特定の理論的分布に従うかを評価します。
- 独立性検定(Test of Independence): クロス集計表の2つの変数の間に関連性があるかを調べます。
F検定とt検定の接点
カイ二乗とF検定:
F検定は、カイ二乗検定に基づいている部分があります。特に、分散分析(ANOVA)は、分散の比をカイ二乗検定の結果として考えることができるため、F統計量はカイ二乗分布を使って計算されます。
カイ二乗とt検定:
t検定の背後にあるデータが正規分布に従う場合、サンプルサイズが十分大きいときは、t分布がカイ二乗分布に接近します。これは、t検定を使用する際に、サンプルの分散を推定する過程でカイ二乗分布が関与するためです。
乗客クラスと生存率の関係(カイ二乗検定)
from scipy.stats import chi2_contingency
# 乗客クラスと生存率のクロス集計
contingency = pd.crosstab(train['Pclass'], train['Survived'])
# カイ二乗検定の実行
chi2, p, dof, expected = chi2_contingency(contingency)
print(f"カイ二乗統計量: {chi2:.4f}, p値: {p:.4f}")出力:
カイ二乗統計量: 102.8890, p値: 0.0000解釈:
- p値が0.0000であり、有意水準5%で帰無仮説を棄却します。つまり、乗客クラスと生存率には統計的に有意な関連があることが示されます。
搭乗場所と生存率の関係(カイ二乗検定)
# 搭乗場所と生存率のクロス集計
contingency = pd.crosstab(train['Embarked'], train['Survived'])
# カイ二乗検定の実行
chi2, p, dof, expected = chi2_contingency(contingency)
print(f"カイ二乗統計量: {chi2:.4f}, p値: {p:.4f}")出力:
カイ二乗統計量: 26.4891, p値: 0.0000p値が0.0000であり、有意水準5%で帰無仮説を棄却します。つまり、搭乗場所と生存率には統計的に有意な関連があることが示されます。
まとめ
今回のブログでは、データの前処理と可視化の重要性について詳しく学びました。データ分析の質を向上させるためには、まずデータのクリーニングや整形が不可欠です。欠損値の処理方法として、削除や平均、中央値、最頻値を用いた補完、さらには機械学習モデルを活用したKNN Imputerについても触れました。最尤法とEMアルゴリズムの概念も理解し、データの特性に応じた適切な処理を行うことができるようになりました。
さらに、カテゴリカルデータのエンコーディング手法や特徴量のスケーリング、外れ値の検出と処理方法についても学びました。これらの技術は、モデルがデータをより効果的に処理できるようにするための基盤となります。また、探索的データ解析(EDA)を通じて、データの深い理解を得るための視覚的手法を使用し、相関分析や箱ひげ図を用いてデータの分布を観察しました。
統計的検定の実施では、性別や乗客クラスと生存率の関係をカイ二乗検定で検証し、カイ二乗検定の理論や他の検定との関連性を学びました。このように、データ前処理と可視化の技術を駆使することで、より信頼性の高いデータ解析が可能となります。
次回予告
次回は「機械学習の基本概念を理解しよう」というテーマで、教師あり学習、教師なし学習、強化学習などの主要な概念を掘り下げていきます。これにより、さまざまな問題に機械学習をどのように適用できるのかを学び、実践的なスキルを身につけていきましょう。お楽しみに!



コメント