【第2回】統計学の基礎

機械学習
2024.10.21
  1. 目的
    1. 第２回の目標
      1. 統計学の重要性
      2. 【第2回】統計学の基礎で用いる数式記号の意味
  2. 記述統計 (Descriptive Statistics) — データの全体像を把握する
    1. 主要な記述統計の指標
        1. 不偏分散とは？
      1. Pythonコード例：記述統計の計算
  3. 推測統計 (Inferential Statistics) — サンプルから母集団を推測する
    1. t検定 (t-test)
        1. t検定の数式（独立2標本の場合）
        2. プールされた分散の数式
      1. t検定における不偏分散とプールされた分散の違い
        1. 不偏分散
        2. プールされた分散（1つの共通の分散として扱うため）
      2. Pythonコード例： t検定の実装
    2. ウェルチのt検定
      1. 独立2標本t検定との違い
      2. ウェルチのt検定の数式
      3. Pythonコード例： ウェルチのt検定の実装
      4. ウェルチのt検定の使い方（Kaggleでの応用）
      5. ウェルチのt検定と独立2標本t検定の比較
  4. 共分散
    1. 共分散とは？
      1. 共分散の数式
      2. Pythonコード例：共分散の計算
        1. 共分散の必要性
  5. 相関分析 (Correlation Analysis) — 変数間の関係性を測定する
      1. 共分散と相関係数の違い
        1. 共分散の数式
        2. 相関係数の数式
      2. Kaggleでの相関分析の実用例
      3. Pythonコード例：特徴量選択 — 相関が高い特徴量を除外する
      4. Pythonコード例：外れ値の検出 — 相関係数の低い特徴量を発見
      5. 共分散と相関係数の使い方（Kaggleでの応用）
  6. 仮説検定 (Hypothesis Testing) — 仮説が正しいかを検証する
    1. 仮説検定の手順
      1. 仮説検定の種類
    2. t検定 (t-test) — 2つのグループの平均を比較する
      1. 独立2標本t検定 (Independent two-sample t-test)
        1. 独立2標本t検定の数式
        2. Pythonコード: 独立2標本t検定の実装
      2. 対応t検定 (Paired t-test)
        1. 対応t検定の数式
      3. Pythonコード：対応t検定の実装
    3. F検定 (F-test) — グループ間の分散を比較する
      1. F検定の数式
      2. Pythonコード： F検定の実装
        1. p値、t値、F値の解釈
          1. p値
          2. t値
          3. F値
      3. 仮説検定におけるt検定とF検定の使い分け
      4. 仮説検定のKaggleでの応用
      5. 特徴量選択を仮説検定で行う具体例
        1. 具体例：家の価格予測モデルにおける特徴量選択
          1. 仮説設定
          2. データ準備
          3. 仮説検定（t検定）の実行
          4. 結果の解釈
          5. 特徴量選択の流れ
        2. 仮説検定を使った特徴量選択のメリット
    4. カイ二乗検定とは？
      1. カイ二乗分布の特徴
      2. 使用される場面
        1. F検定とt検定の接点
  7. まとめ

目的

このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用できる力を養うことが目的です。この過程で、実践的な演習やプロジェクトを通じて、手を動かしながら学ぶ姿勢を大切にしていきます。

第２回の目標

第2回では、機械学習やデータ解析に欠かせない「統計学の基礎」を学びます。統計学は、データを正確に理解し、データが何を示しているのかを判断するための重要なスキルです。

Kaggleのコンペティションに参加するためには、データ解析の基本的な統計手法を正しく理解し、使いこなすことが重要です。今回は、統計学の主要な方法論である記述統計、推測統計、相関分析、仮説検定について、理論とPythonでの実装例を組み合わせて丁寧に解説します。

統計学の重要性

統計学は、データを解釈するための「数学的な言語」です。機械学習において、アルゴリズムはデータをもとに学習します。そのため、データがどのように分布しているか、変動の程度はどれくらいかといった統計的な情報を把握することが非常に重要です。たとえば、平均や標準偏差を知ることで、モデルがデータのパターンを正確に把握できるかどうかがわかります。

【第2回】統計学の基礎で用いる数式記号の意味

数式記号記号の意味
$μ (mu)$母集団の平均
${x}$サンプルデータの各値
$n$サンプルサイズ（データ数）
$σ (sigma)$標準偏差（母集団のばらつきの指標）
$σ²$分散（標準偏差の二乗）
$s²$不偏分散（サンプル分散、母集団の分散の推定）
$t$t統計量（t検定における統計量）
$F$F統計量（F検定における統計量）
$Cov(X, Y)$共分散
$r$相関係数（2変数間の線形関係の強さ）

記述統計 (Descriptive Statistics) — データの全体像を把握する

記述統計は、データセット全体を要約し、データの中心傾向やばらつきを簡潔に表現するための手法です。基本的な指標として、平均、中央値、最頻値、分散、標準偏差が使用されます。

主要な記述統計の指標

  • 平均 (Mean): データの中心的な値で、すべてのデータポイントの合計をデータの数で割ったもの。
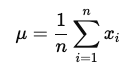
  • 中央値 (Median): データを昇順に並べた際、中央に位置する値。外れ値の影響を受けにくい。
  • 最頻値 (Mode): データの中で最も頻繁に出現する値。
  • 分散 (Variance): データが平均値からどれだけ離れているかを表す指標。
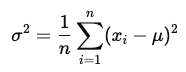
  • 標準偏差 (Standard Deviation): 分散の平方根を取ったもので、データの散らばり具合を直感的に理解しやすい。
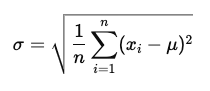
不偏分散とは？

不偏分散は、サンプルデータの分散を母集団の分散の推定として使用する場合に計算されます。不偏分散は、通常のサンプル分散の計算における分母を「サンプル数 n」ではなく「サンプル数 n−1」とすることで、サンプルの分散が母集団の分散を低く見積もってしまうバイアスを修正します。

  • 不偏分散の数式

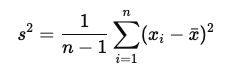
この不偏分散は、母集団の分散を正確に推定するための調整が加えられており、t検定や他の統計的な推測手法において重要な役割を果たします。

Pythonコード例：記述統計の計算

import pandas as pd

# データフレームの作成
df = pd.DataFrame({
    'Scores': [85, 90, 78, 92, 88, 76, 95, 89]
})

# 平均、中央値、最頻値、分散、標準偏差を計算
mean = df['Scores'].mean()
median = df['Scores'].median()
mode = df['Scores'].mode()[0]
variance = df['Scores'].var(ddof=0)  # 通常の分散（偏りがある）
unbiased_variance = df['Scores'].var(ddof=1)  # 不偏分散
std_dev_biased = df['Scores'].std(ddof=0)  # 通常の標準偏差（偏りがある）
std_dev_unbiased = df['Scores'].std(ddof=1)  # 不偏標準偏差


print(f"Mean: {mean}, Median: {median}, Mode: {mode}")
print(f"Variance (biased): {variance}, Unbiased Variance: {unbiased_variance}") 
print(f"Biased Standard Deviation: {std_dev_biased}, Unbiased Standard Deviation: {std_dev_unbiased}")

推測統計 (Inferential Statistics) — サンプルから母集団を推測する

推測統計は、サンプルデータから母集団全体の傾向を推測するための方法です。Kaggleの解析では、データセット全体の傾向を理解したり、特定の変数が重要かどうかを評価するために使用されます。

t検定 (t-test)

t検定は、2つのグループの平均が統計的に有意に異なるかを検証するための方法です。例えば、実験群と対照群の間に差があるかどうかを評価する際に使います。ここでは、独立2標本t検定について説明します。

実験群の例: 新薬を投与された患者の集団。

対照群の例: プラセボ（効果のない偽の薬）を投与された患者の集団。

t検定の数式（独立2標本の場合）
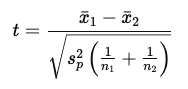
  • $\bar{x}_1, \bar{x}_2​$ はそれぞれのグループの平均
  • $n_1, n_2$ は各グループのサンプルサイズ
  • $s_{p2}$ はプールされた分散（両グループの分散を平均化したもの）で、次のように定義されます。
プールされた分散の数式

$$s_p^2 = \frac{(n_1 – 1)s_1^2 + (n_2 – 1)s_2^2}{n_1 + n_2 – 2}$$

  • $s_1^2, s_2^2$は各グループの不偏分散です。

t検定における不偏分散とプールされた分散の違い

不偏分散

各グループのばらつきを個別に計算する際に用います。不偏分散は、サンプルの分散が母集団の分散を低く見積もるのを防ぐために使用されます。

プールされた分散（1つの共通の分散として扱うため）

独立2標本t検定において、2つのグループの分散が等しいと仮定した場合に、それぞれのグループの分散を加重平均して算出されます。これは、t検定において2つのグループの分散を統合して、1つの共通の分散として扱うために必要です。

プールされた分散の役割：

独立2標本t検定では、2つのグループの分散が等しいという仮定のもとで平均の差を比較します。そのため、t検定の公式では、この「プールされた分散」を使って両グループのデータのばらつきを適切に反映した共通の分散を利用します。

t検定では、不偏分散に基づいて2つのグループの分散を計算し、その分散が等しいと仮定した場合にプールされた分散を使用して平均の差を検定します。

Pythonコード例： t検定の実装

from scipy import stats

# 2つのグループのデータ
group1 = [23, 45, 67, 34, 22, 25, 43, 65]
group2 = [22, 35, 55, 29, 19, 22, 44, 54]

# 独立t検定を実行（分散が等しいと仮定）
t_stat, p_value = stats.ttest_ind(group1, group2, equal_var=True)

print(f"t-statistic: {t_stat}, p-value: {p_value}")

ウェルチのt検定

ウェルチのt検定は、2つの独立したグループの平均を比較する際に、分散が等しくない場合に使用される推測統計手法です。先ほど説明した独立2標本t検定では、2つのグループの分散が等しいと仮定していますが、実際のデータでは分散が等しいとは限りません。そこで、ウェルチのt検定が有効となります。

独立2標本t検定との違い

  • 独立2標本t検定は、2つのグループの分散が等しい（等分散）という仮定のもとに行われます。したがって、分散が等しい場合にはこの検定が推奨されます。
  • ウェルチのt検定は、分散が異なる（不等分散）場合に使われ、分散が等しいという仮定がないため、より現実的なデータに対応できます。

ウェルチのt検定の数式

ウェルチのt検定では、t統計量は以下のように計算されます。

$$t = \frac{\bar{x}_1 – \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}$$

  • $\bar{x}_1, \bar{x}_2​$ はそれぞれのグループの平均、
  • $s_1^2, s_2^2$は各グループの不偏分散です。
  • $n_1, n_2$ は各グループのサンプルサイズ

また、ウェルチのt検定では、自由度が次のように調整されます。

$$df = \frac{\left(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\right)^2}{\frac{\left(\frac{s_1^2}{n_1}\right)^2}{n_1 – 1} + \frac{\left(\frac{s_2^2}{n_2}\right)^2}{n_2 – 1}}$$

この自由度は、通常のt検定よりも複雑ですが、サンプルサイズや分散の違いを考慮するために重要です。

Pythonコード例： ウェルチのt検定の実装

from scipy import stats

# 2つのグループのデータ
group1 = [23, 45, 67, 34, 22, 25, 43, 65]
group2 = [22, 35, 55, 29, 19, 22, 44, 54]

# ウェルチのt検定（分散が等しくないと仮定）
t_stat, p_value = stats.ttest_ind(group1, group2, equal_var=False)

print(f"t-statistic: {t_stat}, p-value: {p_value}")

ウェルチのt検定の使い方（Kaggleでの応用）

Kaggleで使用する場合、ウェルチのt検定は次のような場面で役立ちます。

A/Bテスト：

2つの異なるバージョンのシステム、例えばWebサイトのデザインAとデザインBのコンバージョン率を比較する際、データの分散が異なることが予想される場合に使用します。

実験データの分析：

異なるグループ間で分散が均一でないことが一般的な場合に、ウェルチのt検定が有効です。

Kaggleのデータでは、特定の特徴量が異なるカテゴリでどのように変動するかを見る際に分散の違いが生じることが多いため、分散が等しくない場合はウェルチのt検定が適しています。これは、分散が等しいと仮定するt検定では適切に結果を導き出せない可能性があるためです。

ウェルチのt検定と独立2標本t検定の比較

項目独立2標本t検定ウェルチのt検定
分散の仮定分散が等しいと仮定（等分散）分散が等しくないと仮定（不等分散）
t統計量の計算プールされた分散を使用各グループの分散を別々に扱う
自由度の計算シンプルな計算式調整された自由度が使われる
どのようなデータに適しているか分散が等しいグループ間の比較分散が異なるグループ間の比較
主な用途分散が等しいと見なせるデータ分散が異なるデータ（より現実的なデータ）

ウェルチのt検定は、分散が等しいという仮定をしないため、特に分散が異なるグループを比較する場合に便利です。Kaggleで異なるサンプル群を扱う際、事前に分散が等しいかどうかがわからない場合、ウェルチのt検定はより信頼性の高い結果を提供します。

共分散

共分散は、2つの変数がどの程度同時に変動するかを測定する指標であり、Kaggleのデータ解析でも使用されることがあります。特に、特徴量間の関係性を分析し、モデルの精度向上に役立てるために使われます。共分散は、相関分析の基礎としても重要であり、相関係数の計算にも関連します。

共分散とは？

共分散は、2つの変数 $X$ と $Y$ の間の同時変動を表します。共分散が正の値であれば、2つの変数は同じ方向に変動し、負の値であれば逆の方向に変動します。共分散が0に近い場合は、2つの変数の間に関係がほとんどないことを示しています。

共分散の数式

$${Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (X_i – \bar{X})(Y_i – \bar{Y})$$

  • ${X}_i​$ は変数 ${X}​$ の各値
  • ${Y}_i​$ は変数 ${Y}​$ の各値
  • $\bar{X}, \bar{Y}$ はそれぞれの平均

Pythonコード例：共分散の計算

import numpy as np
import pandas as pd

# データの作成
df = pd.DataFrame({
    'X': [1, 2, 3, 4, 5],
    'Y': [5, 4, 6, 5, 6]
})

# 共分散行列を計算
cov_matrix = np.cov(df['X'], df['Y'], bias=False)
print("Covariance Matrix:\n", cov_matrix)
共分散の必要性

共分散は、2つの変数が同時にどの程度変動するかを測定します。しかし、共分散は変数の単位に依存するため、異なるスケールのデータでは直接比較するのが難しいという欠点があります。たとえば、温度（℃）と収入（円）の共分散を直接比較しても、スケールが違うため意味が不明瞭です。

共分散は、相関係数を計算する基礎的な指標として非常に重要です。特に、Kaggleで特徴量間の関係性を分析し、モデルの性能向上に役立てる際、共分散は特徴量同士の相互作用を理解する助けになります。

相関分析 (Correlation Analysis) — 変数間の関係性を測定する

相関分析は、2つの変数間にどの程度の関係があるかを確認するための統計手法です。Kaggleでのデータ解析では、特徴量間の関係性を理解することで、どの特徴量がモデルの精度向上に寄与するか、または逆に冗長性があるかを把握することが重要です。

相関分析は、データセットの特徴を理解し、適切な特徴量選択を行うための重要なステップであり、以下の流れで進めます。

  1. データの視覚化: まず、変数間の関係を直感的に理解するために、散布図やヒートマップなどを使って視覚化します。
  2. 相関係数の計算: 次に、変数間の相関関係を定量的に測定するために、相関係数を計算します。
  3. 結果の解釈: 最後に、相関係数に基づいて、2つの変数がどの程度強く関連しているかを判断します。

共分散と相関係数の違い

共分散と相関係数はどちらも変数間の関係を測定する手法ですが、次のような違いがあります。

  • 共分散は、2つの変数がどの程度一緒に変動するかを測定します。ただし、共分散は変数の単位に依存するため、スケールが異なる変数間では比較が難しいという欠点があります。
  • 相関係数は、共分散を各変数の標準偏差で正規化したもので、単位に依存せず、-1から1の範囲で関係性を示します。相関係数は、データのスケールにかかわらず、異なる変数間の関係性を比較するために使用されます。
共分散の数式

$${Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (X_i – \bar{X})(Y_i – \bar{Y})$$

  • ${X}_i​$ は変数 ${X}​$ の各値
  • ${Y}_i​$ は変数 ${Y}​$ の各値
  • $\bar{X}, \bar{Y}$ はそれぞれの平均
相関係数の数式

$$r = \frac{\text{Cov}(X, Y)}{\sigma_X \sigma_Y}$$

  • $\sigma_X \sigma_Y$​ はそれぞれの変数の標準偏差です。

相関係数は、2つの変数の間にどの程度の線形関係があるかを測定する指標です。相関係数は、-1から1の間で表され、次のように解釈されます。

  • 1に近い場合：2つの変数は強い正の相関があり、一方が増加するともう一方も増加する傾向があります。
  • -1に近い場合：2つの変数は強い負の相関があり、一方が増加するともう一方は減少する傾向があります。
  • 0に近い場合：2つの変数の間にはほとんど線形関係がありません。

相関係数は、共分散を標準偏差で正規化したものです。これにより、スケール（単位）が異なる変数間でも、関係性を比較できるようになります。

Kaggleでの相関分析の実用例

Kaggleでは、データの探索的解析（EDA）において、相関分析が重要です。たとえば、次のような場面で使われます。

特徴量選択：

相関の高い特徴量がある場合、冗長な情報を削除するために、相関係数を用いて不要な特徴量を除外します。

外れ値の検出：

相関係数が異常に低い特徴量がある場合、その特徴量に外れ値が含まれている可能性があり、外れ値の特定と修正に役立ちます。

Pythonコード例：特徴量選択 — 相関が高い特徴量を除外する

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# サンプルデータフレームの作成
data = {
    'Feature1': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
    'Feature2': [2, 4, 6, 8, 10, 12, 14, 16, 18, 20],  # Feature1と高い相関を持つ
    'Feature3': [1, 2, 2, 3, 4, 4, 5, 6, 7, 8]         # Feature1と相関が弱い
}
df = pd.DataFrame(data)

# 相関行列の計算
correlation_matrix = df.corr()

# ヒートマップで相関を可視化
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm')
plt.title('Correlation Matrix')
plt.show()

# 相関係数が高すぎる特徴量を検出
threshold = 0.9  # 相関の閾値
high_correlation_features = [col for col in correlation_matrix.columns if any(correlation_matrix[col] > threshold) and col != correlation_matrix.columns[0]]

print(f"High correlation features (correlation > {threshold}): {high_correlation_features}")

# 高い相関がある特徴量を除外
df_reduced = df.drop(columns=high_correlation_features)
print("Reduced DataFrame:\n", df_reduced)

出力：

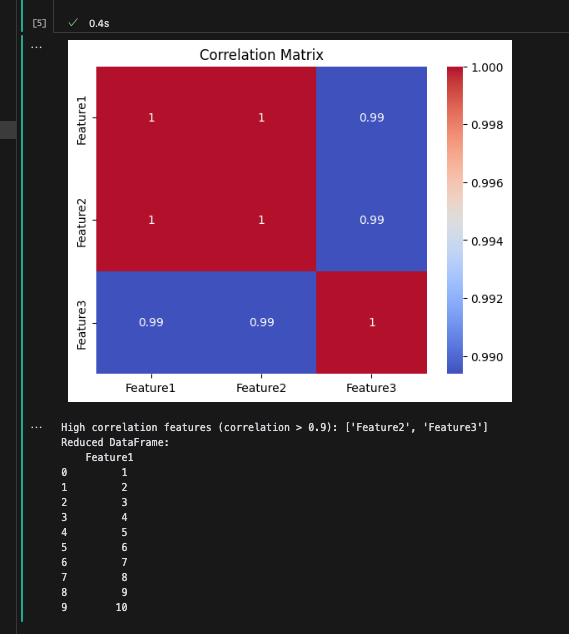
コードの説明：

  • このコードでは、Feature1 と Feature2 が強い相関（1に近い相関係数）を持っているため、thresholdで定義された閾値を超える特徴量を削除しています。この場合、Feature2は冗長な情報として削除されます。
  • ヒートマップで相関行列を視覚化し、どの特徴量が強く関連しているかを確認できます。

Pythonコード例：外れ値の検出 — 相関係数の低い特徴量を発見

外れ値を検出するために、相関係数を用いて特定の変数が期待された相関を持っていないかどうかを調べます。相関係数が異常に低い特徴量が含まれている場合、外れ値が原因の可能性があるため、確認と修正を行います。

# サンプルデータフレームの作成（外れ値を含む）
data_outliers = {
    'Feature1': [1, 2, 3, 4, 5, 6, 7, 100, 9, 10],   # 外れ値 100
    'Feature2': [2, 4, 6, 8, 10, 12, 14, 16, 18, 20]
}
df_outliers = pd.DataFrame(data_outliers)

# 相関行列の計算
correlation_matrix_outliers = df_outliers.corr()

# ヒートマップで相関を可視化
sns.heatmap(correlation_matrix_outliers, annot=True, cmap='coolwarm')
plt.title('Correlation Matrix with Outlier')
plt.show()

# 外れ値がある場合、相関係数が低くなる可能性を確認
print("Correlation Matrix with Outlier:\n", correlation_matrix_outliers)

# 外れ値の検出（異常な値を持つ行を確認）
outliers = df_outliers[df_outliers['Feature1'] > 50]
print("Detected Outliers:\n", outliers)

出力：

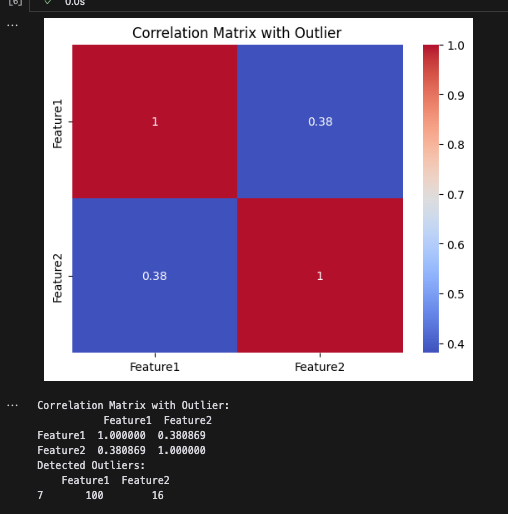
コードの説明：

  • Feature1には明らかに外れ値である100が含まれています。この外れ値により、Feature1とFeature2の間の相関が低くなることがわかります。
  • このコードでは、Feature1の値が一定の閾値を超える行を外れ値として検出し、修正のために特定しています。

Kaggleでの実務では、これらの手法を使ってデータをクレンジングし、モデルのパフォーマンスを最適化することがよく行われます。

共分散と相関係数の使い方（Kaggleでの応用）

使う場面使い方
特徴量選択
相関が高い特徴量を特定し、不要な特徴量を削除。
多重共線性の回避モデルの精度向上のために、相関係数を確認し、多重共線性を回避。
特徴量エンジニアリング相関を基に新たな特徴量を作成し、モデルの性能を向上。
外れ値の検出とデータのクレンジング外れ値を発見し、データをクレンジング。
予測モデルの解釈モデルの解釈を補助し、予測結果の解釈を深める。

仮説検定 (Hypothesis Testing) — 仮説が正しいかを検証する

仮説検定は、データに基づいて特定の仮説が統計的に有意かどうかを判断するための手法です。Kaggleでのデータ解析においても、重要な変数やモデルの性能を評価するために頻繁に使用されます。仮説検定を使うことで、2つ以上のグループ間に違いがあるか、モデルの優位性があるかなど、統計的な判断を行うことができます。

この章では、仮説検定の基本的な流れを理解し、t検定とF検定の使い方やその違いについて詳しく説明します。t検定には対応t検定と独立2標本t検定があり、それぞれの用途や特徴についても解説します。また、p値、t値、F値についても詳しく説明し、仮説検定を深く理解するための手助けをします。

仮説検定の手順

  1. 帰無仮説 (H0​)： 「効果がない」「差がない」と仮定する仮説。例えば、「2つのグループの平均に差はない」など。
  2. 対立仮説 (H1​)：帰無仮説に反する仮説。「効果がある」「差がある」といった内容を含む。例えば、「2つのグループの平均に有意な差がある」など。
  3. 検定量の計算：t値やF値を用いて、データから統計量を計算します。
  4. p値の算出：検定統計量に基づいて、帰無仮説が正しい確率（p値）を計算します。
  5. 結論の導出: p値が事前に設定した有意水準 (α=0.05) 未満であれば、帰無仮説を棄却し、対立仮説を採用します。つまり、差や効果があると判断します。

仮説検定の種類

仮説検定には多くの種類がありますが、このブログではt検定とF検定を中心に解説します。

t検定 (t-test) — 2つのグループの平均を比較する

t検定は、2つのグループ間の平均に有意な差があるかどうかを検証するために使用されます。t検定には、次の2種類があります。

独立2標本t検定 (Independent two-sample t-test)

独立2標本t検定は、異なる2つの独立したグループの平均を比較するために使用します。データはグループごとに独立しており、たとえば異なる学校の2クラスのテストスコアなどが該当します。

使用例：

異なる集団（グループAとグループB）のテストスコアの平均に差があるかどうかを比較する。

独立2標本t検定の数式

$$t = \frac{\bar{x}_1 – \bar{x}_2}{\sqrt{s_p^2 \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}}
$$

  • $\bar{x}_1, \bar{x}_2​$ はそれぞれのグループの平均
  • $n_1, n_2$ は各グループのサンプルサイズ
  • $s_{p2}$ はプールされた分散（両グループの分散を平均化したもの）で、次のように定義されます。
Pythonコード: 独立2標本t検定の実装
from scipy import stats

# 2つの独立したグループのデータ（異なるグループのテストスコア）
group1 = [85, 90, 88, 75, 95, 80, 87, 91]
group2 = [77, 82, 79, 72, 85, 78, 80, 86]

# 独立2標本t検定を実行
t_stat, p_value = stats.ttest_ind(group1, group2)

print(f"t-statistic: {t_stat}, p-value: {p_value}")

# 結果の解釈
alpha = 0.05
if p_value < alpha:
    print("帰無仮説を棄却します。2つのグループに有意な差があります。")
else:
    print("帰無仮説を採用します。2つのグループに有意な差はありません。")

対応t検定 (Paired t-test)

対応t検定は、同じ対象に対する2つの条件を比較するために使用します。データはペアとなっており、たとえば同じ被験者の治療前後の結果を比較する場合に適しています。

使用例：

同じ患者が治療前と治療後に血圧を測定した場合や、同じ学生が異なる条件でテストを受けた結果を比較する場合。

対応t検定の数式

$$t = \frac{\bar{d}}{s_d / \sqrt{n}}$$

  • $\bar{d}$ はペアの差分の平均
  • ${s_d}$ は差分の標準偏差
  • ${n}$ はペアのサンプルサイズです。

Pythonコード：対応t検定の実装

from scipy import stats

# 2つの対応するグループのデータ（同じ被験者のテスト前後のスコア）
before_treatment = [85, 90, 88, 75, 95, 80, 87, 91]
after_treatment = [87, 92, 90, 76, 97, 82, 89, 93]

# 対応t検定を実行
t_stat, p_value = stats.ttest_rel(before_treatment, after_treatment)

print(f"t-statistic: {t_stat}, p-value: {p_value}")

# 結果の解釈
alpha = 0.05
if p_value < alpha:
    print("帰無仮説を棄却します。治療前後で有意な差があります。")
else:
    print("帰無仮説を採用します。治療前後で有意な差はありません。")

F検定 (F-test) — グループ間の分散を比較する

F検定は、2つ以上のグループの分散が等しいかどうかを検証するために使用されます。例えば、複数のモデル間の分散を比較する際に役立ちます。また、分散分析（ANOVA）の基本的な手法としても使われます。

F検定の数式

$$F = \frac{\text{偏差の分散}}{\text{残差の分散}} = \frac{MS_{\text{偏差}}}{MS_{\text{残差}}}$$

  • 分散が等しい場合、F値は1に近くなります。
  • ${MS}$は「Mean Square」の略で、統計学において「平均平方」を表します。

Pythonコード： F検定の実装

from scipy import stats

# Levene検定を使って分散の等質性を検定
group1 = [85, 90, 88, 75, 95, 80, 87, 91]
group2 = [77, 82, 79, 72, 85, 78, 80, 86]

f_stat, p_value = stats.levene(group1, group2)

print(f"F-statistic: {f_stat}, p-value: {p_value}")

# 結果の解釈
alpha = 0.05
if p_value < alpha:
    print("帰無仮説を棄却します。2つのグループの分散に有意な差があります。")
else:
    print("帰無仮説を採用します。2つのグループの分散に有意な差はありません。")
p値、t値、F値の解釈
p値

p値は、帰無仮説が正しいと仮定した場合に、観測されたデータが得られる確率です。p値が有意水準 (α=0.05)よりも小さい場合、帰無仮説を棄却します。

t値

t値は、2つのグループの平均の差が、そのデータの分散に対してどれだけ大きいかを示します。t値が大きいほど、グループ間の平均の差が統計的に有意である可能性が高くなります。t検定では、t値が有意水準に対応するt分布の臨界値を超えるかどうかを見て、帰無仮説を棄却するかどうかを判断します。

F値

F値は、2つ以上のグループ間の分散の比率を示す指標です。F値が1に近ければ、グループ間の分散はほぼ等しいことを示し、F値が大きくなればグループ間の分散が大きく異なることを示します。F検定では、F値に基づいて分散の違いが有意であるかどうかを判断します。

仮説検定におけるt検定とF検定の使い分け

t検定：

2つのグループの平均の差を検証したい場合に使用します。特に、2つの独立したグループ（独立2標本t検定）や同じグループの異なる時点でのデータ（対応t検定）を比較する際に有効です。

F検定：

2つ以上のグループの分散の差を検証する際に使用します。複数のモデルやグループ間のばらつきを評価するために使われ、特に分散分析 (ANOVA)で重要な役割を果たします。

仮説検定のKaggleでの応用

Kaggleのデータ解析や機械学習モデルの評価において、仮説検定は以下のような場面で使われます。

A/Bテスト: 新しい機能やデザインの有効性を確認するために、2つのグループ間の平均差を検証します。t検定を使用して、2つのバージョンに有意な差があるかどうかを評価します。

特徴量選択: ある特徴量がターゲット変数に与える影響が有意かどうかを仮説検定で検証します。仮説検定によって有意な特徴量を特定し、モデルに有効な変数を絞り込むことができます。

モデル評価: 異なるモデルの性能を比較する際、F検定を使用してモデル間の分散の違いを評価し、どのモデルが最も適しているかを判断します。

特徴量選択を仮説検定で行う具体例

仮説検定を使って特徴量選択を行う場合、ターゲット変数（目的変数）と各特徴量（説明変数）の関係を評価し、それが統計的に有意かどうかを検証します。仮説検定により、有意な特徴量を特定し、不要な特徴量を除外することで、モデルの精度を向上させることができます。

ここでは、t検定を使用して、連続変数のターゲット変数に対して、2つのグループ間で特徴量の平均が異なるかを検証し、有意な特徴量を選択する例を示します。

具体例：家の価格予測モデルにおける特徴量選択

あるデータセットには、家の価格（ターゲット変数）を予測するために、家のサイズ、部屋数、築年数などの特徴量があります。ここで、例えば「エリアA」と「エリアB」の2つのエリアに分かれている場合、エリアの特徴量が家の価格に有意な影響を与えるかを仮説検定で確認します。

仮説設定
  • 帰無仮説 (H₀): エリアAとエリアBで家の価格に差はない。
  • 対立仮説 (H₁): エリアAとエリアBで家の価格に有意な差がある。
データ準備

仮に、エリアAとエリアBにおける家の価格のデータが以下のようにあるとします。

import pandas as pd
from scipy import stats

# データセットの作成
data = {
    'Price': [350000, 450000, 370000, 560000, 300000, 420000, 470000, 620000, 320000, 500000, 340000, 520000],
    'Area': ['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B', 'B', 'B']
}

df = pd.DataFrame(data)

# エリアAとエリアBの価格データを分ける
area_A = df[df['Area'] == 'A']['Price']
area_B = df[df['Area'] == 'B']['Price']
仮説検定（t検定）の実行

次に、エリアAとエリアBで家の価格に有意な差があるかどうかをt検定で確認します。

# 独立2標本t検定を実行
t_stat, p_value = stats.ttest_ind(area_A, area_B)

print(f"t-statistic: {t_stat}, p-value: {p_value}")
結果の解釈

仮説検定を実行すると、次のような結果が得られます。

# 出力
t-statistic: -0.8181520709541856, p-value: 0.4323332851327527

この結果から、p値が0.43であるため、通常の有意水準（α=0.05\alpha = 0.05α=0.05）を下回っていません。したがって、帰無仮説を棄却できません。つまり、エリアAとエリアBの間で家の価格に有意な差はないと結論づけられます。

この例では、エリアという特徴量が家の価格に対して有意な影響を与えていないと判断され、特徴量としてモデルに含める必要はないと解釈されます。

特徴量選択の流れ

このように仮説検定を使って、各特徴量がターゲット変数に対して有意な影響を与えているかを調べます。結果として、有意な特徴量だけを選び出し、モデルに取り入れることができます。

仮説検定を使った特徴量選択のメリット
  1. 有意な特徴量を特定：統計的に意味のある特徴量を選択し、不要な特徴量を除去することで、モデルの解釈性とパフォーマンスを向上させます。
  2. モデルの過学習防止：関連のない特徴量を排除することで、過学習を防ぎ、モデルの汎化性能を向上させます。

カイ二乗検定とは？

カイ二乗検定（Chi-squared test）は、観測データが期待される分布とどれほど一致しているかを評価するための統計的手法です。主にカテゴリーデータに対して使用され、以下の2つの主なタイプがあります。

適合度検定（Goodness-of-fit test）：

観測データが特定の理論的分布に従っているかどうかを検定します。

独立性検定（Test of independence）：

2つのカテゴリ変数の間に関連性があるかどうかを検定します。

$$\chi^2 = \sum \frac{(O_i – E_i)^2}{E_i}$$

$χ2$カイ二乗統計量
$Oi​$各カテゴリにおける観測頻度（実際のデータの値）
$Ei​$各カテゴリにおける期待頻度（理論的に予測された値）
$i$カテゴリのインデックス

カイ二乗統計量は、各カテゴリにおける観測値と期待値の差の平方を期待値で割り、その合計を求めます。この計算により、観測データが期待分布からどれだけ離れているかを定量的に示します。

カイ二乗分布の特徴

  1. 自由度（Degrees of Freedom）: カイ二乗分布は自由度によって形状が決まります。自由度は、データの中で独立して変化できるパラメータの数を示します。自由度が増加するにつれて、カイ二乗分布の形は正規分布に近づきます。
  2. 非対称性: カイ二乗分布は非対称で、右に尾を引く形をしています。自由度が少ないときは、特に尖った形をしており、自由度が大きくなるにつれて平坦になります。
  3. 0以上の値: カイ二乗分布は0以上の値のみを取るため、負の値は存在しません。これは、カイ二乗統計量が観測値と期待値の差の平方の和であるためです。

使用される場面

  • 適合度検定（Goodness-of-Fit Test）: 観測データが特定の理論的分布に従うかを評価します。
  • 独立性検定（Test of Independence）: クロス集計表の2つの変数の間に関連性があるかを調べます。
F検定とt検定の接点

カイ二乗とF検定：

F検定は、カイ二乗検定に基づいている部分があります。特に、分散分析（ANOVA）は、分散の比をカイ二乗検定の結果として考えることができるため、F統計量はカイ二乗分布を使って計算されます。

カイ二乗とt検定：

t検定の背後にあるデータが正規分布に従う場合、サンプルサイズが十分大きいときは、t分布がカイ二乗分布に接近します。これは、t検定を使用する際に、

from scipy.stats import chi2_contingency
# 性別と生存率のクロス集計
contingency = pd.crosstab(train['Sex'], train['Survived'])
# カイ二乗検定の実行
chi2, p, dof, expected = chi2_contingency(contingency)
print(f"カイ二乗統計量: {chi2:.4f}, p値: {p:.4f}")

# 出力
# カイ二乗統計量: 260.7170, p値: 0.0000

p値が0.0000であり、有意水準5%で帰無仮説を棄却します。つまり、性別と生存率には統計的に有意な関連があることが示されます。

まとめ

今回は、Kaggleで役立つ統計手法の基本について学びました。記述統計によってデータの特徴を把握し、推測統計で母集団の特性を推測し、相関分析を用いて特徴量間の関係性を明らかにしました。また、仮説検定とF分布、カイニ乗検定を用いたデータ解析の重要性についても確認しました。

次回は、これらの統計手法を活用し、データの前処理と可視化に焦点を当てた機械学習アルゴリズムの適用方法について学んでいきます。データのクリーニングや欠損値の処理、特徴量エンジニアリングの具体的な手法を取り上げ、データの質を向上させ、視覚的に理解する技術を習得します。

次回もお楽しみに！

コメント

タイトルとURLをコピーしました