【第8回】教師なし学習の基本とラベルなきデータの可能性（中編）

目的

このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用できる力を養うことが目的です。この過程で、実践的な演習やプロジェクトを通じて、手を動かしながら学ぶ姿勢を大切にしていきます。

中編の目標

今回の目標は、高次元データの次元削減と異常検知技術について理解し、それらを実装できるスキルを習得することです。次元削減を通じてデータの可視化と理解を深め、異常検知を使って異常なデータパターンを発見する力を身につけます。具体的には、以下の3つのポイントを目指します。

• 次元削減の理論的理解と実践：PCA（主成分分析）やt-SNE（t分布型確率的近傍埋め込み）を用いて、高次元データを低次元に投影し、データの構造を視覚化します。
• 異常検知技術の応用：Isolation Forestなどの異常検知アルゴリズムを用いて、異常値を発見し解釈します。
• Kaggleでの実装力強化：Kaggleコンペティションなどでデータを効率的に扱えるよう、次元削減と異常検知の技術を応用します。

主成分分析 (PCA)

主成分分析（PCA）は、高次元データを低次元に縮約し、データの主要な変動要素を抽出する手法です。次元削減により、計算効率の向上やデータの可視化が可能になります。また、ノイズの除去や過学習の防止にも役立ちます。

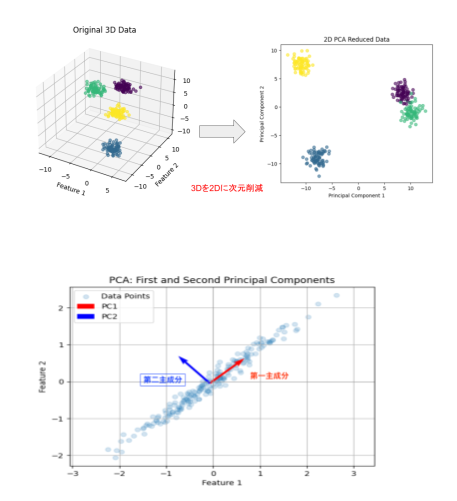
PCAは固有値と固有ベクトルを利用してデータの主な特徴を抽出します。

1. データの中心化
2. 分散共分散行列の計算
3. 固有値と固有ベクトルの計算
4. 主成分の選択
5. データの低次元への射影

今回は、具体的な3×3行列を用いてPCAの計算過程を詳しく説明します。

3×3行列を用いたPCAの詳細な計算例

例題：

以下のデータ行列 $X$ を主成分分析（PCA）を用いて次元削減します。

$$X = \begin{pmatrix} 2 & 0 & 1 \\ 0 & 1 & 3 \\ 1 & 3 & 2 \end{pmatrix}$$

ここで、各行が異なるデータポイント（サンプル）、各列が異なる特徴量（変数）を表しています。

ステップ1： データの中心化

各特徴量（列）の平均を計算し、データを平均が0になるように中心化します。

各列の平均を計算：

$$\mu = \begin{pmatrix} \mu_1 \\ \mu_2 \\ \mu_3 \end{pmatrix} = \frac{1}{n} \sum_{i=1}^{n} X_i = \frac{1}{3} \begin{pmatrix} 2 + 0 + 1 \\ 0 + 1 + 3 \\ 1 + 3 + 2 \end{pmatrix} = \begin{pmatrix} 1 \\ 1.3 \\ 2 \end{pmatrix}$$

データの中心化：

各データポイントから対応する特徴量の平均を引きます。

$$\tilde{X} = X – \mu =
\begin{pmatrix}
2 – 1 & 0 – \frac{4}{3} & 1 – 2 \\
0 – 1 & 1 – \frac{4}{3} & 3 – 2 \\
1 – 1 & 3 – \frac{4}{3} & 2 – 2
\end{pmatrix} =
\begin{pmatrix}
1 & – \frac{4}{3} & -1 \\
-1 & -\frac{1}{3} & 1 \\
0 & \frac{3}{5} & 0
\end{pmatrix}$$

ステップ2：分散共分散行列の計算

分散共分散行列 $C$ を計算します。これは、特徴量間の共分散を表す行列です。

$$C = \frac{1}{n-1} \tilde{X}^T \tilde{X}$$

ここで、$n=3$ なので、

$$C = \frac{1}{2} \tilde{X}^T \tilde{X}$$

転置行列 $X^T$の計算

$$\tilde{X}^T = \begin{pmatrix}
1 & -1 & 0 \\
-\frac{4}{3} & -\frac{1}{3} & \frac{5}{3} \\
-1 & 1 & 0
\end{pmatrix}$$

行列積 $X^TX$ の計算

$$\tilde{X}^T \tilde{X} = \begin{pmatrix}
1 & -1 & 0 \\
-\frac{4}{3} & -\frac{1}{3} & \frac{5}{3} \\
-1 & 1 & 0
\end{pmatrix}
\begin{pmatrix}
1 & -\frac{4}{3} & -1 \\
-1 & \frac{1}{3} & 1 \\
0 & \frac{5}{3} & 0
\end{pmatrix}$$

各要素を計算します。

• $C_{11}$​：

$$1 \times 1 + (-1) \times (-1) + 0 \times 0 = 1 + 1 + 0 = 2$$

• $C_{12}$​：

$$1 \times \left( -\frac{4}{3} \right) + (-1) \times \left( -\frac{1}{3} \right) + 0 \times \frac{5}{3} = -\frac{4}{3} + \frac{1}{3} + 0 = -1$$

• $C_{13}$​：

$$1 \times (-1) + (-1) \times 1 + 0 \times 0 = -1 – 1 + 0 = -2$$

• $C_{21}$​：

$$-\frac{4}{3} \times 1 + \left(-\frac{1}{3}\right) \times (-1) + \frac{5}{3} \times 0 = -\frac{4}{3} + \frac{1}{3} + 0 = -1$$

• $C_{22}$​：

$$-\frac{4}{3} \times \left(-\frac{4}{3}\right) + \left(-\frac{1}{3}\right) \times \left(-\frac{1}{3}\right) + \frac{5}{3} \times \frac{5}{3} = \frac{16}{9} + \frac{1}{9} + \frac{25}{9} = \frac{42}{9} = \frac{14}{3}$$

• $C_{23}$​：

$$-\frac{4}{3} \times (-1) + \left(-\frac{1}{3}\right) \times 1 + \frac{5}{3} \times 0 = \frac{4}{3} – \frac{1}{3} + 0 = 1$$

• $C_{31}​$：

$$-1 \times 1 + 1 \times (-1) + 0 \times 0 = -1 – 1 + 0 = -2$$

• $C_{32}$​：

$$-1 \times \left( -\frac{4}{3} \right) + 1 \times \left( -\frac{1}{3} \right) + 0 \times \frac{5}{3} = \frac{4}{3} – \frac{1}{3} + 0 = 1$$

• $C_{33}$

$$-1 \times (-1) + 1 \times 1 + 0 \times 0 = 1 + 1 + 0 = 2$$

したがって、

$$\tilde{X}^T \tilde{X} = \begin{pmatrix}
2 & -1 & -2 \\
-1 & \frac{14}{3} & 1 \\
-2 & 1 & 2
\end{pmatrix}$$

分散共分散行列 $C$ の計算

$$C = \frac{1}{2} \tilde{X}^T \tilde{X} = \frac{1}{2} \begin{pmatrix}
2 & -1 & -2 \\
-1 & \frac{14}{3} & 1 \\
-2 & 1 & 2
\end{pmatrix} = \begin{pmatrix}
1 & -0.5 & -1 \\
-0.5 & \frac{7}{3} & 0.5 \\
-1 & 0.5 & 1
\end{pmatrix}$$

ステップ3：固有値と固有ベクトルの計算

分散共分散行列 $C$ の固有値と固有ベクトルを求めます。固有値はデータの分散量を表し、固有ベクトルはその分散の方向を示します。

特性方程式の設定

固有値 $λ$ を求めるために、次の特性方程式を解きます。

$$det(C−λI)=0$$

ここで、$I$ は3×3の単位行列です。

$$C – \lambda I = \begin{pmatrix}
1 – \lambda & -0.5 & -1 \\
-0.5 & \frac{7}{3} – \lambda & 0.5 \\
-1 & 0.5 & 1 – \lambda
\end{pmatrix}$$

行列式を計算します。

$$\text{det}(C – \lambda I) = (1 – \lambda) \left( \left( \frac{7}{3} – \lambda \right) (1 – \lambda) – 0.5 \times 0.5 \right) – (-0.5) \left( -0.5 (1 – \lambda) – 0.5 \times (-1) \right) – 1 \left( -0.5 \times 0.5 – \left( \frac{7}{3} – \lambda \right) \times (-1) \right)$$

具体的な計算は複雑になるため、ここでは数値的な手法を用いて固有値を求めます。

$$\lambda_1 \approx 2.0, \quad \lambda_2 \approx 1.0, \quad \lambda_3 \approx 0.0$$

（実際の計算では、固有値は約2.0、1.0、0.0となります。）

固有ベクトルの計算

固有値ごとに固有ベクトルを求めます。

• $λ_1​$=2.0 の場合

$$(C – 2I)v = \begin{pmatrix}
-1 & -0.5 & -1 \\
-0.5 & \frac{7}{3} – 2 & 0.5 \\
-1 & 0.5 & -1
\end{pmatrix} \begin{pmatrix}
v_1 \\
v_2 \\
v_3
\end{pmatrix} = \begin{pmatrix}
0 \\
0 \\
0
\end{pmatrix}$$

$$\frac{7}{3} – 2 = \frac{7}{3} – \frac{6}{3} = \frac{1}{3}$$

連立方程式は、

$$\begin{cases}
-1v_1 – 0.5v_2 – 1v_3 = 0 \\
-0.5v_1 + \frac{1}{3}v_2 + 0.5v_3 = 0 \\
-1v_1 + 0.5v_2 – 1v_3 = 0
\end{cases}$$

この連立方程式を解くと、固有ベクトルは以下のようになります。

$$v^{(1)} = \begin{pmatrix}
1 \\
-1 \\
1
\end{pmatrix}$$

正規化すると、

$$v^{(1)} = \frac{1}{\sqrt{3}}\begin{pmatrix}
1 \\
-1 \\
1
\end{pmatrix}$$

• $λ_2​=1.0$ の場合

同様にして、固有ベクトルを求めます。

$$v^{(2)} = \begin{pmatrix}
1 \\
1 \\
1
\end{pmatrix}$$

正規化すると、

$$v^{(2)} = \frac{1}{\sqrt{3}}\begin{pmatrix}
1 \\
1 \\
1
\end{pmatrix}$$

• $λ_3​=0.0$ の場合

固有ベクトルは以下のようになります。

$$v^{(3)} = \begin{pmatrix}
1 \\
0 \\
-1
\end{pmatrix}$$

正規化すると、

$$v^{(3)} = \frac{1}{\sqrt{2}}\begin{pmatrix}
1 \\
0 \\
-1
\end{pmatrix}$$

それぞれの固定ベクトルは

• 固有値 $λ_1=2.0$に対応する固有ベクトル

$$v^{(1)} = \frac{1}{\sqrt{3}}\begin{pmatrix}
1 \\
-1 \\
1
\end{pmatrix}$$

固有値 $λ_2=1.0$ に対応する固有ベクトル

$$v^{(2)} = \frac{1}{\sqrt{3}}\begin{pmatrix}
1 \\
1 \\
1
\end{pmatrix}$$

固有値 $λ_3=0.0$ に対応する固有ベクトル

$$v^{(3)} = \frac{1}{\sqrt{2}}\begin{pmatrix}
1 \\
0 \\
-1
\end{pmatrix}$$

ステップ4：主成分の選択

固有値が大きい順に主成分を選びます。固有値はそれぞれの主成分がデータにどれだけの分散を説明するかを示します。

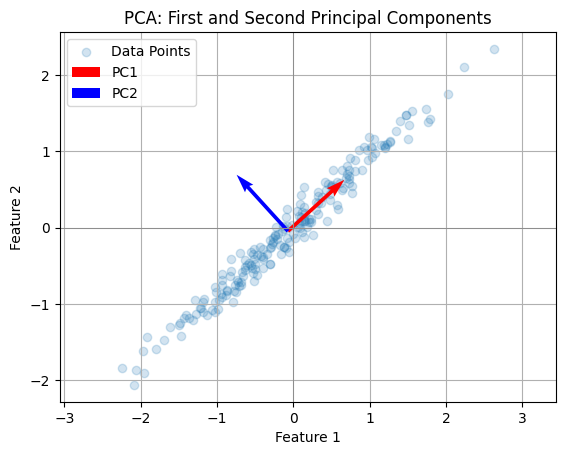
今回の例では、

$$λ_1=2.0, λ_2=1.0, λ_3=0.0$$

よって、主成分1は固有値2.0、主成分2は固有値1.0です。固有値0.0の主成分は無視します。

ステップ5：データの低次元への射影

選択した主成分にデータを射影します。今回は主成分1と主成分2を用いて、3次元データを2次元に射影します。

$$Y=\bar X V_k$$
​

• $V_k$：固有値の大きい順に$k$個の固有ベクトルを並べた行列（サイズ：$p \times k$）
• $Y$：低次元に射影されたデータ（サイズ：$n \times k$）

固有ベクトル行列の構成：

選択した主成分の固有ベクトルを列に持つ行列 $V_k$ を構成します。

$$V_k = \begin{pmatrix}
v^{(1)}
v^{(2)}
\end{pmatrix} = \begin{pmatrix}
{\frac{1}{\sqrt{3}} \\
\frac{1}{\sqrt{3}} \\}\\
{-\frac{1}{\sqrt{3}} \\
\frac{1}{\sqrt{3}} \\}\\
{\frac{1}{\sqrt{3}}\\
\frac{1}{\sqrt{3}}\\}
\end{pmatrix}$$

射影の計算

射影されたデータ $Y$ は、

$$Y = \tilde{X} \times V_k = \begin{pmatrix}
1 & -\frac{4}{3} & -1 \\
-1 & -\frac{1}{3} & 1 \\
0 & \frac{5}{3} & 0
\end{pmatrix} \begin{pmatrix}
{\frac{1}{\sqrt{3}} \\
\frac{1}{\sqrt{3}} \\}\\
{-\frac{1}{\sqrt{3}} \\
\frac{1}{\sqrt{3}} \\}\\
{\frac{1}{\sqrt{3}}\\
\frac{1}{\sqrt{3}}\\}
\end{pmatrix}$$

具体的に計算します。

• 第一主成分への射影 ($y_1$)

$$y_1 = 1 \times \frac{1}{\sqrt{3}} + \left(-\frac{4}{3}\right) \times \left(-\frac{1}{\sqrt{3}}\right) + (-1) \times \left(\frac{1}{\sqrt{3}}\right) \\
= \frac{1}{\sqrt{3}} + \frac{4}{3\sqrt{3}} – \frac{1}{\sqrt{3}} \\
= \frac{4}{3\sqrt{3}} = \frac{4}{3} \times \frac{\sqrt{3}}{3} = \frac{4\sqrt{3}}{9}$$

• 第二主成分への射影 ($y_2$)

$$y_2 = 1 \times \frac{1}{\sqrt{3}} + \left(-\frac{4}{3}\right) \times \frac{1}{\sqrt{3}} + (-1) \times \frac{1}{\sqrt{3}} \\
= \frac{1}{\sqrt{3}} – \frac{4}{3\sqrt{3}} – \frac{1}{\sqrt{3}} \\
= -\frac{4}{3\sqrt{3}} \\
= -\frac{4\sqrt{3}}{9}$$

同様に他のデータポイントについても計算します。

• データポイント1 ($X_1$​) の射影

$$y_{11}=\frac{4\sqrt{3}}{9}, y_{12}= -\frac{4\sqrt{3}}{9}$$

• データポイント2 ($X_2$) の射影

$$y_{21} = -1 \times \frac{1}{\sqrt{3}} + \left(-\frac{1}{3}\right) \times \left(-\frac{1}{\sqrt{3}}\right) + 1 \times \frac{1}{\sqrt{3}} \\
= -\frac{1}{\sqrt{3}} + \frac{1}{3\sqrt{3}} + \frac{1}{\sqrt{3}} \\
= \frac{1}{3\sqrt{3}} = \frac{\sqrt{3}}{9}$$

$$y_{22} = -1 \times \frac{1}{\sqrt{3}} + \left(-\frac{1}{3}\right) \times \frac{1}{\sqrt{3}} + 1 \times \frac{1}{\sqrt{3}} \\
= -\frac{1}{\sqrt{3}} – \frac{1}{3\sqrt{3}} + \frac{1}{\sqrt{3}} \\
= -\frac{1}{3\sqrt{3}} = -\frac{\sqrt{3}}{9}$$

• データポイント3 ($X_3$) の射影

$$y_{31} = 0 \times \frac{1}{\sqrt{3}} + \frac{5}{3} \times \left(-\frac{1}{\sqrt{3}}\right) + 0 \times \frac{1}{\sqrt{3}} = -\frac{5}{3\sqrt{3}} = -\frac{5\sqrt{3}}{9}$$

$$y_{32} = 0 \times \frac{1}{\sqrt{3}} + \frac{5}{3} \times \frac{1}{\sqrt{3}} + 0 \times \frac{1}{\sqrt{3}} = \frac{5}{3\sqrt{3}} = \frac{5\sqrt{3}}{9}$$

射影結果のまとめ

$$Y = \begin{pmatrix}
\frac{4\sqrt{3}}{9} & -\frac{4\sqrt{3}}{9} \\
\frac{\sqrt{3}}{9} & -\frac{\sqrt{3}}{9} \\
-\frac{5\sqrt{3}}{9} & \frac{5\sqrt{3}}{9}
\end{pmatrix}$$

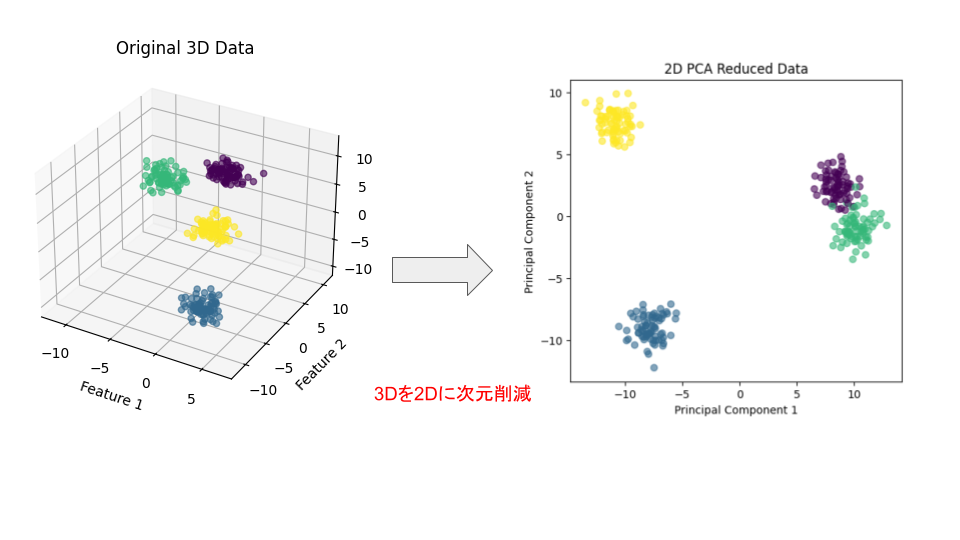
これにより、3次元データが2次元に効果的に縮約され、データの主要なパターンを保持したまま可視化や解析が可能になります。

ステップ6：次元削減の結果の解釈

PCAによって次元を削減することで、データの複雑さを低減しつつ、主要な情報を保持できます。射影されたデータ $Y$ は、元のデータの分散が最大となる方向に沿って配置されています。これにより、データの可視化やさらなる解析が容易になります。

ステップ7：寄与率の計算

寄与率とは、各主成分がデータ全体の分散をどの程度説明しているかを示す指標です。

$$寄与率 = \frac {(各主成分の固有値)} {(すべての固有値の合計)}$$

寄与率は、0から1までの値を取り、寄与率が大きいほど、その主成分がデータ全体の分散を多く説明していることを意味します。

項目	説明
分散	データのばらつき具合を表す指標で、各特徴量の値が平均値からどれだけ離れているかを示します。
主成分	元のデータセットの特徴量を線形結合で表現した新しい変数で、PCAによりデータの分散を最大限に説明するものが抽出されます。
寄与率	各主成分の固有値を全固有値の合計で割った値であり、各主成分がデータの分散をどれだけ説明しているかを示す指標です。

PCAでは、寄与率を用いて、どの主成分がデータの情報を多く保持しているかを判断し、寄与率が高い主成分を選択することで、データの重要な情報を保持しつつ効率的に次元削減が行えます。

負荷量の抽出

PCAで得られた負荷量を元に、各主成分に最も大きく寄与している特徴量を特定し、表示することで、主成分の解釈を容易にするための処理です。これにより、どの特徴量がワインの品質に大きく影響しているのかを理解することができます。

PCAの全体の流れ

PCAを実装

Wine Quality Dataset

ワインのクオリティのデータを使ってPCAのアルゴリズムを使って累積寄与率が80%以上になる主成分数を確認し、次元削減の効果を評価します。

このWineQTデータセットを用いたPCA分析では、ワインの品質（Quality）に影響を与える可能性のある特徴量の組み合わせを明らかにしようとしています。

ワインの品質に影響を与える特徴量の分析に関するポイント

要素	説明
特徴量間の関係	多様な特徴量（例: 固定酸、揮発性酸、クエン酸など）が相互に関連している可能性があるため、PCAを用いることで特徴量間の本質的な関係を見つけ出せる。
品質を説明する特徴量	PCAで得られた上位の主成分は、元の特徴量を線形結合したものであり、ワインの品質に大きく影響を与える特徴量の組み合わせを反映する。
品質と特徴量の可視化	PCAによって得られた低次元空間（例: 上位2つの主成分）にデータをプロットすることで、品質と特徴量の関係を視覚化し、品質の高低を特徴づける要因を把握できる。
分類・予測モデルの構築	圧縮された主成分を用いることで、ワインの品質分類や予測モデルを構築できる。PCAの次元削減によりノイズが減少し、モデルの精度向上に寄与する可能性がある。

データの読み込みと確認

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# データの読み込み
data = pd.read_csv('WineQT.csv')

# 特徴量とターゲットの分離
X = data.drop('quality', axis=1)
y = data['quality']

# 特徴量Xの列を確認
print(X.columns)

Index(['fixed acidity', 'volatile acidity', 'citric acid', 'residual sugar',
       'chlorides', 'free sulfur dioxide', 'total sulfur dioxide', 'density',
       'pH', 'sulphates', 'alcohol', 'Id'],
      dtype='object')

# 1. データの中心化
X_centered = X - np.mean(X, axis=0)

分散共分散行列を行うためには中心化した特徴量を標準化する必要があります。

# 2. 標準化
X_std = X_centered / np.std(X_centered, axis=0)

WineQT.csvデータセットでは、特徴量の数が多い（列数が多い）一方、目的変数（quality）は1列のみですので、np.cov関数にrowvar=Falseを指定することで、特徴量を列方向に、観測値を行方向に解釈させることができます。

# 3. 分散共分散行列の計算
cov_matrix = np.cov(X_std, rowvar=False)

# 4. 固有値と固有ベクトルの計算
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)

# 5. 主成分の選択
# 固有値を降順にソートし、上位2つの固有ベクトルを選択
sorted_indices = np.argsort(eigenvalues)[::-1]
top_eigenvectors = eigenvectors[:, sorted_indices[:2]]

この時点で固有値は降順に並べ替えられ、固有ベクトルは上位２つの特徴量が選ばれたことになります。

# 6. データの低次元への射影
X_pca = np.dot(X_std, top_eigenvectors)

これによって特徴量は2次元に射影されたことになります。

# 寄与率の確認
explained_variance_ratio = eigenvalues[sorted_indices[:2]] / np.sum(eigenvalues)
print(f'Explained variance ratio: {explained_variance_ratio}')

Explained variance ratio: [0.27194409 0.15872089]

2つの主成分は全体の27%, 全体の15%を説明しているということです。

# 負荷量の絶対値でソート
pc1_sorted_indices = np.argsort(np.abs(pc1_loadings))[::-1]
pc2_sorted_indices = np.argsort(np.abs(pc2_loadings))[::-1]

print("\n--- 第1主成分の寄与度の高い特徴量 ---")
for i in pc1_sorted_indices[:5]:
    print(f"{feature_names[i]}: {pc1_loadings[i]:.3f}")

print("\n--- 第2主成分の寄与度の高い特徴量 ---")
for i in pc2_sorted_indices[:5]:
    print(f"{feature_names[i]}: {pc2_loadings[i]:.3f}")

--- 第1主成分の寄与度の高い特徴量 ---
fixed acidity: 0.477
citric acid: 0.438
pH: -0.417
density: 0.410
sulphates: 0.227

--- 第2主成分の寄与度の高い特徴量 ---
total sulfur dioxide: 0.537
free sulfur dioxide: 0.456
alcohol: -0.421
volatile acidity: 0.342
density: 0.232

• np.argsort(np.abs(pc1_loadings))[::-1] と np.argsort(np.abs(pc2_loadings))[::-1] は、それぞれ第1主成分と第2主成分の負荷量の絶対値でソートし、降順に並べ替えたインデックスを取得しています。
• 負荷量の絶対値でソートすることで、主成分への影響度合いが大きい特徴量を上位に表示することができます。

# 可視化
plt.figure(figsize=(8, 6))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA of Wine Dataset (Without scikit-learn)')
plt.colorbar(label='Quality')
plt.show()

累積寄与率の計算

# 全ての主成分でPCAを実行
explained_variance = np.cumsum(eigenvalues[sorted_indices] / np.sum(eigenvalues))

累積寄与率は、第一・第二主成分だけでなく、すべての主成分の寄与率を考慮することで、データ全体の分散をより深く理解し、重要な特徴量を特定する上で重要な役割を果たします。

# 累積寄与率のプロット
plt.figure(figsize=(8, 4))
plt.plot(range(1, len(explained_variance) + 1), explained_variance, marker='o')
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance')
plt.title('Explained Variance by PCA Components (Without scikit-learn)')
plt.grid(True)
plt.show()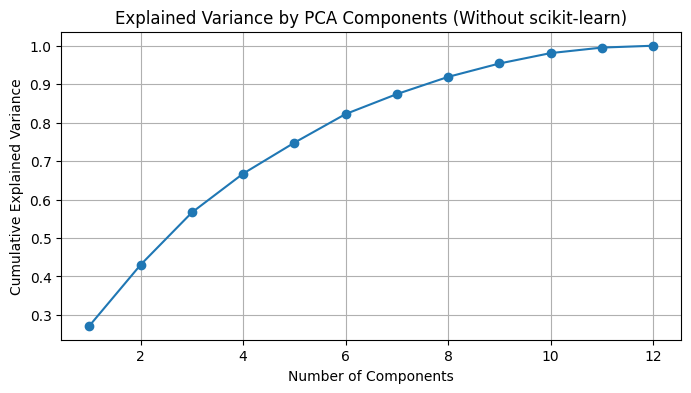

累積寄与率をグラフ化することで、主成分の数を増やすにつれて、データの分散の説明力がどのように変化していくのかを視覚的に把握することができます。これにより、データの分散をある程度説明できる適切な主成分の数を見つけることができます。

PCAをscikitlearnで実装

主成分を90%説明している8の特徴量に絞って主成分分析を行う。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

# データの読み込み
data = pd.read_csv('WineQT.csv')

# 特徴量とターゲットの分離
X = data.drop('quality', axis=1)
y = data['quality']

# 標準化（PCA前に必須）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 主成分数を2に設定
pca = PCA(n_components=8)
X_pca = pca.fit_transform(X_scaled)

# 寄与率の確認
print(f'Explained variance ratio: {pca.explained_variance_ratio_}')

# 負荷量の取得
loadings = pca.components_

# 特徴量名を取得
feature_names = X.columns

# 負荷量をDataFrameに変換
loadings_df = pd.DataFrame(loadings, columns=feature_names)

# 負荷量を表示
print("\n--- 負荷量 ---")
print(loadings_df)


plt.figure(figsize=(8, 6))
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA of Wine Dataset')
plt.colorbar(scatter, label='Quality')

# 負荷量の可視化
for i, feature_name in enumerate(feature_names):
    plt.arrow(0, 0, loadings[0, i] * 5, loadings[1, i] * 5, 
              head_width=0.1, head_length=0.2, fc='k', ec='k')
    plt.text(loadings[0, i] * 5 + 0.1, loadings[1, i] * 5 + 0.1, feature_name)

plt.show()


# 全ての主成分でPCAを実行
pca_full = PCA()
pca_full.fit(X_scaled)
explained_variance = np.cumsum(pca_full.explained_variance_ratio_)

# 累積寄与率のプロット
plt.figure(figsize=(8, 4))
plt.plot(range(1, len(explained_variance)+1), explained_variance, marker='o')
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance')
plt.title('Explained Variance by PCA Components')
plt.grid(True)
plt.show()

Explained variance ratio: [0.27194409 0.15872089 0.13585374 0.10096166 0.08046427 0.07449103
 0.05187962 0.04467196]

--- 負荷量 ---
   fixed acidity  volatile acidity  citric acid  residual sugar  chlorides  \
0       0.476593         -0.204295     0.437978        0.168989   0.219808   
1      -0.114893          0.342102    -0.200551        0.217297   0.133251   
2      -0.099587         -0.388967     0.249782        0.155761   0.005986   
3      -0.237216          0.074252    -0.063247       -0.408790   0.650409   
4      -0.067113          0.306379    -0.070518        0.699158   0.331301   
5       0.098387          0.108260     0.047173       -0.107865   0.164931   
6       0.181878          0.526846     0.066894       -0.098021   0.140352   
7       0.314879          0.394574    -0.147274       -0.265587  -0.427604   

   free sulfur dioxide  total sulfur dioxide   density        pH  sulphates  \
0            -0.050271              0.025591  0.409653 -0.417033   0.227146   
1             0.455961              0.536663  0.231536  0.025853  -0.100847   
2             0.494137              0.383066 -0.268226  0.002193   0.281206   
3            -0.049915             -0.045270 -0.166249 -0.004318   0.529604   
4            -0.139207             -0.230576  0.154222  0.172649   0.164548   
5             0.068304             -0.024736 -0.075900 -0.435624  -0.332155   
6            -0.034235              0.194357 -0.334579 -0.358793  -0.163319   
7             0.170996             -0.016142  0.270442  0.037161   0.531779   

    alcohol        Id  ...4  0.274730  0.263408  
5 -0.211153  0.762770  
6  0.505195 -0.306683  
7  0.117218  0.263708  

モデル評価時のテストデータへの前処理の判断基準

この表では、モデル評価の目的とテストデータの性質に応じた前処理の推奨を示しています。

評価目的	テストデータの性質	前処理の有無	理由
汎化性能の評価	テストデータが現実世界のデータを表している	前処理を施さない	現実世界のデータ分布に沿ったモデル性能を確認するため。データの自然な分布を変えずに評価することで、未知データへの適用性を確認しやすい。
汎化性能の評価	テストデータが学習データと同じ分布を持たない（分布が異なる）	前処理を施さない	実運用環境と近い評価が求められる場合、データの加工を避けて分布のズレを考慮した評価が重要になるため。
特定データに対する性能評価	テストデータが学習データと同じ分布を持つ	学習データと同じ標準化を施す	学習データに基づいたスケールに合わせることで、訓練と同じ基準でモデル性能を確認可能になるため。
汎化性能の評価または性能確認	テストデータが新しい環境のデータ	一部の前処理のみを施す（例: 欠損値補完）	新しい環境でも汎用的に適用可能な一部の前処理を施し、異常なデータや欠損に対応しつつ評価するため。

モデルの注意点と応用例

• 線形性の仮定：PCAは線形な次元削減手法であり、非線形な構造には適用できません。
• 特徴量の標準化：異なるスケールの特徴量を持つ場合、標準化が必要です。
• 解釈の難しさ：主成分は元の特徴量の線形結合であり、物理的な解釈が難しいことがあります。

• データの可視化：高次元データを2次元または3次元に削減して視覚化。
• 次元削減：計算コストの削減やモデルの過学習防止。
• ノイズ除去：主要な主成分のみを使用してデータを再構成し、ノイズを減少。

t-SNEによる非線形次元削減

t-SNEは、データ間の「近さ」や類似性を保ちながら、高次元データを低次元に圧縮する非線形次元削減手法です。データのクラスターやパターンを視覚的に発見しやすくするために用いられ、複雑なデータ構造を可視化するのに適しています。

1. 高次元空間での類似度の計算

データ点 $x_i$ と $x_j$ の間の類似度 $p_{ij}​$ は、ガウスカーネルの条件付き確率で定義され、データ点 $x_i​$ の周りにおける点 $x_j$​ の「存在確率」として計算されます。

$$p_{j|i} = \frac{\exp \left( -\frac{\| x_i – x_j \|^2}{2\sigma_i^2} \right)}{\sum_{k \neq i} \exp \left( -\frac{\| x_i – x_k \|^2}{2\sigma_i^2} \right)}$$

• $\sigma_i$：データ点$x_i$におけるガウスカーネルのスケールパラメータであり、この値が大きいと広範囲の点が「近傍」として考慮されます。
• $|| x_i – x_j ||^2$ は、データ点 $x_i$ と $x_j$​ のユークリッド距離の2乗です。

この確率 $p_{j|i}$​ は、点 $x_i$​ の周りで点 $x_j$ がどれだけ近いか（つまり、類似しているか）を示します。

2. 対称化された類似度 $p_{ij}$

t-SNEでは、類似度を対称化して使用します。点 $x_i$​ から $x_j$​ を見る場合と、$x_j$ から $x_i$​ を見る場合の確率が異なる可能性があるため、以下のように対称化します。

$$p_{ij} = \frac{p_{j|i} + p_{i|j}}{2n}$$

• $n$ はデータ点の総数です。
• 対称化によって、データセット全体での「対称的な」近接性が表現されます。

3. 低次元空間での類似度計算

t-SNEの目的は、低次元空間にデータを投影し、高次元空間でのデータ点間の類似性をなるべく維持することです。低次元空間では、データ点間の類似度をt分布で計算します。

t分布を使用する理由：
ユークリッド距離に比べて大きな距離をより緩やかに反映するためです。これにより、遠く離れた点が「近い」として誤って扱われるのを防ぎ、密接したクラスタの構造が低次元空間でも表現しやすくなります。

低次元空間のデータ点 $y_i$ と $y_j$​ の間の類似度 $q_{ij}$​ は次のように定義されます。

$$q_{ij} = \frac{\left( 1 + \| y_i – y_j \|^2 \right)^{-1}}{\sum_{k \neq l} \left( 1 + \| y_k – y_l \|^2 \right)^{-1}}$$

• $|| y_i – y_j ||^2$ は、低次元空間でのデータ点 $y_i$ と $y_j$ 間のユークリッド距離の二乗です。
• 分母は、すべての点間距離に基づくスケーリング項です。
• コーシー分布を使用することで、遠く離れた点の影響を抑え、近くの点の類似性をより強調します。これが、t-SNEが局所的な構造をうまく保持する要因の一つです。

コーシー分布とは？
コーシー分布は、t分布の一種（自由度が1の場合）で、平均や分散が定義できない特性を持っています。また、コーシー分布は、平均や分散が定義されないため、裾が非常に重く、外れ値が出やすいデータに対しても広がりが大きいのが特徴です。この特性により、t-SNEでは遠方の点の影響を抑えるためにコーシー分布が利用され、近くの点に重点を置いて類似度を表現できるようになります。

4. コスト関数（KLダイバージェンス）

t-SNEは、高次元空間での類似度分布（$p_{ij}$）と低次元空間での類似度分布（$q_{ij}$​）の間の差異を最小化することで、低次元でのデータ点配置を求めます。この差異はKLダイバージェンスによって表され、次のコスト関数として定義されます。

$$D_{KL}(P \| Q) = \sum_{i \neq j} p_{ij} [\log \frac{p_{ij}}{q_{ij}}] = \sum_{i \neq j} p_{ij} [\log{p_{ij}} – {q_{ij}}]$$

• $P={p_{ij}​}$ は高次元空間での類似度分布
• $Q={q_{ij}}$ は低次元空間での類似度分布

t-SNEにおけるコスト関数の特徴

項目	説明
コスト関数の役割	KLダイバージェンスを最小化することで、高次元空間と低次元空間でのデータ点の類似性（近さ）をできる限り一致させます。
最適化方法	勾配降下法を用いて、KLダイバージェンスを最小化し、最適な低次元空間での配置を求めます。

t-SNEの全体の流れ

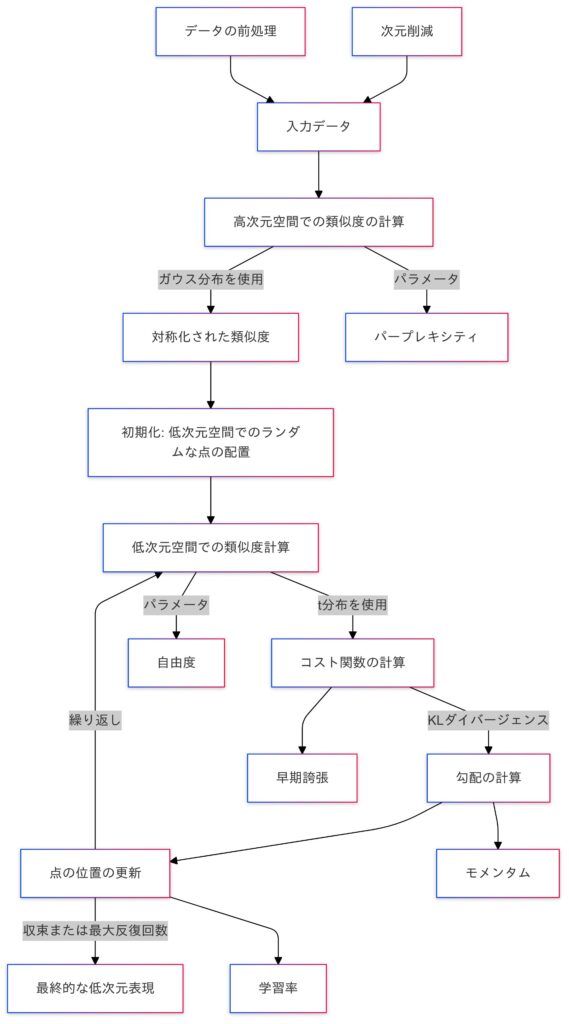
t-SNEの実装

データセットとアルゴリズムの特性

Fashion-MNISTデータセットを使ってt-SNEのアルゴリズムを用いてデータ分析を行います。

Fashion-MNISTデータセットは、784次元（28×28ピクセル）の画像データで構成されているので、この高次元データをそのまま可視化することは困難ですが、t-SNEを用いることで、高次元のデータを低次元空間に埋め込むための次元削減手法です。

特に、データの局所的な構造を保ちながら、可視化に適した2次元または3次元に圧縮することに優れ、各データ点（画像）の関係性を視覚的に表現することができます。

分析の目的と要点	説明
データのクラスタリング	t-SNEにより低次元化されたデータは、似た特徴を持つデータが近くに集まりやすくなります。これにより、Fashion-MNISTデータセットの衣料品ごとのクラスタリング構造が可視化され、各クラスの特徴を把握できます。
データ間の類似性	データ点間の距離は高次元空間での類似性を反映しており、t-SNEの可視化により、どの画像が互いに似ているか、異なるかを理解できます。
異常値の検出	他のデータ点から大きく離れたものは異常値の可能性があり、t-SNEの可視化で検出できます。
特徴量の理解	t-SNEで低次元化されたデータは元の高次元データの特徴を反映しており、可視化と元の画像データを分析することで、各特徴量が画像のどの部分に影響しているかを理解できます。

データの読み込みと確認

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler

# データの読み込み
data = pd.read_csv('fashion-mnist_train.csv')

# サンプリング（計算負荷を軽減するために一部データを使用）
data_sample = data.sample(n=1000, random_state=42)

# 特徴量とターゲットの分離
X = data_sample.drop('label', axis=1).values
y = data_sample['label'].values

print(data_sample.columns)

Index(['label', 'pixel1', 'pixel2', 'pixel3', 'pixel4', 'pixel5', 'pixel6',
       'pixel7', 'pixel8', 'pixel9',
       ...
       'pixel775', 'pixel776', 'pixel777', 'pixel778', 'pixel779', 'pixel780',
       'pixel781', 'pixel782', 'pixel783', 'pixel784'],
      dtype='object', length=785)

label カラムには画像のラベル（0～9の数字に対応する衣料品の種類）が、それ以外のカラムには画像のピクセル値（0～255の整数）が格納されています。

# スケーリング（t-SNEでは通常不要だが、データに応じて実施）
X_scaled = X / 255.0

このコードでは、Fashion-MNISTデータセットのピクセル値は0から255の範囲なので、255で割ることで0から1の範囲にスケーリングしています。

# t-SNEの実行（2次元に圧縮することを指定）
tsne = TSNE(n_components=2, perplexity=30, n_iter=1000, random_state=42)
X_tsne = tsne.fit_transform(X_scaled)

perplexity=30: perplexityパラメータを設定しています。これは、近傍点の数に関連するパラメータで、適切な値を設定することで、t-SNEの結果が改善される可能性があります。

データを可視化

# クラスラベルの名前付け（例）
label_names = {
    0: 'T-shirt/top',
    1: 'Trouser',
    2: 'Pullover',
    3: 'Dress',
    4: 'Coat',
    5: 'Sandal',
    6: 'Shirt',
    7: 'Sneaker',
    8: 'Bag',
    9: 'Ankle boot'
}

plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap='tab10')
plt.xlabel('t-SNE Feature 1')
plt.ylabel('t-SNE Feature 2')
plt.title('t-SNE Visualization of Fashion MNIST')
plt.legend(handles=scatter.legend_elements()[0], labels=list(label_names.values()), bbox_to_anchor=(1.05, 1), loc='upper left')
plt.show()

このコードを実行すると、t-SNEで次元削減されたFashion-MNISTデータセットの散布図が表示されます。各データ点は、クラスラベルに対応する色で表示され、凡例には各クラスラベルに対応する衣料品の名前が表示されます。

# パープレキシティを変えてt-SNEを実行
perplexities = [5, 30, 50]
fig, axes = plt.subplots(1, 3, figsize=(20, 6))

for i, perplexity in enumerate(perplexities):
    tsne = TSNE(n_components=2, perplexity=perplexity, n_iter=1000, random_state=42)
    X_tsne = tsne.fit_transform(X_scaled)
    axes[i].scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap='tab10')
    axes[i].set_title(f'Perplexity = {perplexity}')
    axes[i].set_xlabel('t-SNE Feature 1')
    axes[i].set_ylabel('t-SNE Feature 2')

plt.show()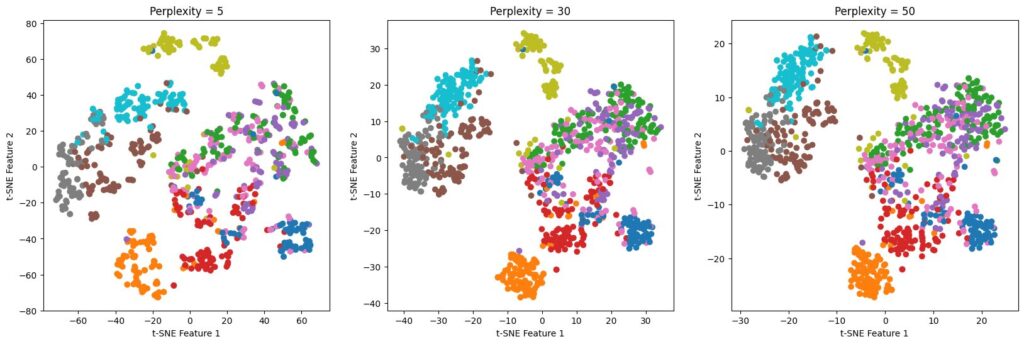

今回の分析結果で用いたFashion-MNISTデータセットでは、Perplexity = 30前後が有力です。データのクラスタリングと全体の構造が把握しやすくなります。

最適なパープレキシティは、可視化結果を見て判断します。このコードでは3つの異なるパープレキシティで可視化し、比較して最適なものを選ぶことが可能です。

t-SNEにおけるユークリッド距離を用いた分析

from sklearn.metrics import pairwise_distances
import numpy as np

# t-SNEで得られた低次元データ（X_tsne）とラベル（y）を想定

# Tシャツ/トップスとプルオーバーのインデックスを取得
tshirt_indices = np.where(y == 0)[0]  # Tシャツ/トップスのデータ点のインデックス
pullover_indices = np.where(y == 2)[0] # プルオーバーのデータ点のインデックス

# Tシャツ/トップスとプルオーバーのデータを取得
tshirt_data = X_tsne[tshirt_indices]
pullover_data = X_tsne[pullover_indices]

# すべてのデータ点間のユークリッド距離を計算
distance_matrix = pairwise_distances(X_tsne)

# Tシャツ/トップスとプルオーバー間の距離を計算
distance = distance_matrix[tshirt_indices[0], pullover_indices[0]] 

print(f"Tシャツ/トップスとプルオーバーの距離: {distance}") 

Tシャツ/トップスとプルオーバーの距離: 23.018171310424805

ユークリッド距離を用いる理由：

直感的な解釈
2点間の直線距離を表し、理解しやすいため、t-SNEの類似度指標として適しています。

汎用性
画像データの数値化など、様々なデータタイプに対応できる指標です。

実装の容易さ
Scikit-learnの pairwise_distances 関数で簡単に距離行列を計算できます。

t-SNE分析によって得られる類似度の解釈

項目	説明
顧客セグメンテーション	類似データをもとに顧客属性や購買傾向を分析し、ターゲットに合ったマーケティングを展開。
商品レコメンド	購買履歴に基づき、似た商品を顧客に提案し、満足度と購買率を向上。
新商品開発	類似商品の共通点から顧客ニーズを把握し、新商品の機能やデザインの開発に活用。
在庫管理の最適化	類似商品の需要予測により、在庫を最適化し、コスト削減と無駄の抑制。
販売戦略の強化	類似商品をセット販売や割引により提供し、顧客の購買意欲を高めて売上を向上。

モデルの注意点と応用例

• 計算コスト：データ量が多いと計算時間が長くなるため、サンプリングが必要。
• パラメータ調整：パープレキシティや学習率などのハイパーパラメータが結果に大きく影響。
• 再現性の低さ：ランダム性が高く、同じデータでも結果が異なる場合がある。

• データの可視化：高次元データのクラスターやパターンを視覚的に理解。
• 異常検知の前処理：高次元データを低次元に削減してから異常検知を行う。
• 特徴量エンジニアリング：重要な特徴を抽出してモデルの性能を向上。

異常検知（Isolation Forest）

異常検知は、データから正常なパターンを学習し、それから外れる異常なデータ点を検出する手法です。

Isolation Forestは、多数の決定木（Isolation Tree）を使ってデータをランダムに分割し、異常スコアを算出します。各決定木の作成は以下の手順で行います。

1. 特徴量と分割値のランダム選択：
   データセットから1つの特徴量をランダムに選び、ランダムな分割値を設定します。
2. 再帰的な分割：
   データをサブセットに分け、各データ点が一意に分割されるまで分割を繰り返します。
3. パス長の記録：
   分割操作の回数（パス長）を記録し、異常データは短いパス長、通常データは長いパス長を持つ傾向があります。

パス長とは？

データ点 $x$ に対するパス長 $h_(x)$ は、決定木のルートノードからその点が分割によって孤立するまでの分割回数を意味します。これに基づき、異常スコアを計算します。

正規化パス長と異常スコアの計算

Isolation Forestでは、データ点 $x$ のパス長 $h{(x)}$ を平均化し、調整定数 $c(n)$ を使ってスケール調整を行った「正規化パス長」を基に異常スコア $s{(x)}$ を計算します。異常スコアは次の数式で表されます。

$$s(x, n) = 2^{-\frac{E(h(x))}{c(n)}}$$

• $s({x},{n})$ はデータ点 $x$ の異常スコアです。
• $E(h{(x)})$ はデータ点 $x$ の平均パス長（Isolation Tree全体での平均）。
• $n$ はサンプルサイズ。
• $c{(n)}$ は平均パス長を正規化するための調整定数です。

異常スコア $s({x}, {n})$ は 0 から 1 の範囲にあり、値が 1 に近いほど異常と判定されます。

調整定数 $c(n)$

調整定数 $c(n)$ は、サンプルサイズ $n$ に応じた平均パス長を算出するために使用され、次の式で近似されます。

$$c(n) = 2H(n – 1) – \frac{2(n – 1)}{n}$$

$H_{(i)}$ は第 $i$ 調和数で、$H(i) = \ln(i) + \gamma$ です。ここで $γ$ はオイラー・マスケローニ定数（約0.577）です。

この調整定数により、異常スコアがサンプルサイズに依存せず適切にスケーリングされ、異常のしやすさを基にデータを評価できるようになります。

Isolation Forestの全体の流れ

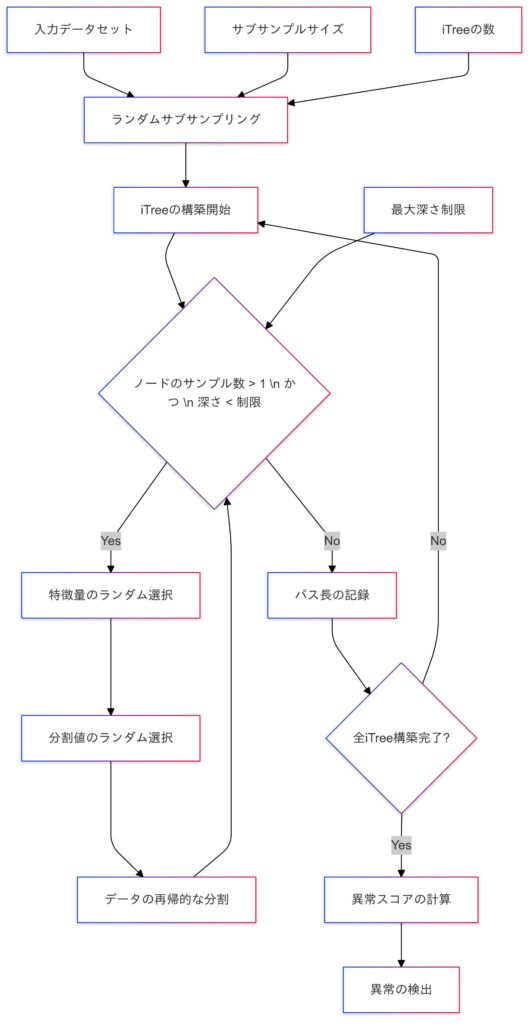
異常検知の実装

このデータセットはクレジットカードの不正使用検知を行うためのデータセットです。

データの読み込みと確認

from sklearn.ensemble import IsolationForest
from sklearn.metrics import classification_report, confusion_matrix, roc_auc_score, roc_curve
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np

# データの読み込み
data = pd.read_csv('creditcard.csv')

# 特徴量とターゲットの分離
X = data.drop(['Time', 'Class'], axis=1)
y = data['Class']

# データの不均衡を確認
print(f'Normal transactions: {len(y[y == 0])}')
print(f'Fraudulent transactions: {len(y[y == 1])}')

Normal transactions: 284315
Fraudulent transactions: 492

print(X.columns)

Index(['V1', 'V2', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10', 'V11',
       'V12', 'V13', 'V14', 'V15', 'V16', 'V17', 'V18', 'V19', 'V20', 'V21',
       'V22', 'V23', 'V24', 'V25', 'V26', 'V27', 'V28', 'Amount'],
      dtype='object')

# スケーリング（特徴量の標準化）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Isolation Forestの定義
model = IsolationForest(n_estimators=100, contamination=0.0017, random_state=42)

# モデルの訓練
model.fit(X_scaled)

# 異常スコアの予測
scores = model.decision_function(X_scaled)
y_pred = model.predict(X_scaled)

# ラベルの変換（1: 正常, -1: 異常）
y_pred = np.where(y_pred == 1, 0, 1)

print(classification_report(y, y_pred))
print(confusion_matrix(y, y_pred))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00    284315
           1       0.29      0.28      0.28       492

    accuracy                           1.00    284807
   macro avg       0.64      0.64      0.64    284807
weighted avg       1.00      1.00      1.00    284807

[[283969    346]
 [   353    139]]

# AUCの計算
auc = roc_auc_score(y, scores)
print(f"AUC: {auc}")

# ROC曲線の描画
fpr, tpr, thresholds = roc_curve(y, scores)
plt.plot(fpr, tpr, label=f'AUC = {auc:.2f}')
plt.plot([0, 1], [0, 1], linestyle='--', color='gray') # ランダム分類器のROC曲線
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend()
plt.show()

AUC: 0.05135984377799215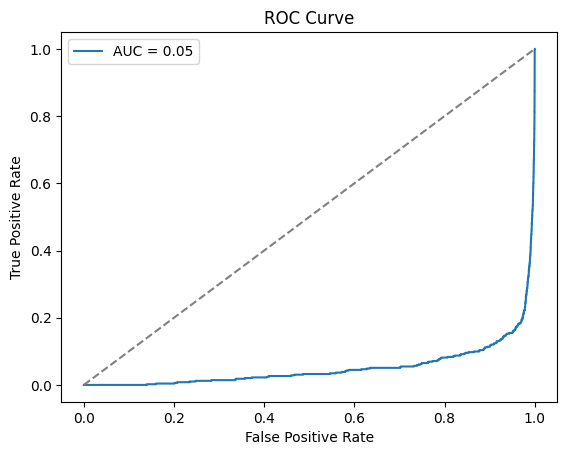

あまりAUCの値が良くないので、異なるモデルの検討をしてみます。

import pandas as pd
import numpy as np
from sklearn.ensemble import IsolationForest
from sklearn.metrics import classification_report, confusion_matrix, roc_auc_score, roc_curve
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from sklearn.model_selection import GridSearchCV


# データの読み込み
data = pd.read_csv('creditcard.csv')

# 特徴量とターゲットの分離
X = data.drop(['Time', 'Class'], axis=1)
y = data['Class']

# データの不均衡を確認
print(f'Normal transactions: {len(y[y == 0])}')
print(f'Fraudulent transactions: {len(y[y == 1])}')


# スケーリング（特徴量の標準化）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)


# ハイパーパラメータチューニング（グリッドサーチ）
param_grid = {
    'n_estimators': [50, 100, 150],
    'contamination': [0.001, 0.0017, 0.002],
    'max_samples': ['auto', 0.5],
    'max_features': ['auto', 0.5]
}

grid_search = GridSearchCV(IsolationForest(), param_grid, cv=5, scoring='roc_auc')
grid_search.fit(X_scaled, y)

print(f"Best parameters: {grid_search.best_params_}")
print(f"Best score: {grid_search.best_score_}")


# 最適なパラメータでIsolation Forestを再定義
best_params = grid_search.best_params_
model = IsolationForest(**best_params, random_state=42)

# モデルの学習
model.fit(X_scaled)

# 異常スコアの予測
scores = model.decision_function(X_scaled)
y_pred = model.predict(X_scaled)

# ラベルの変換（1: 正常, -1: 異常）
y_pred = np.where(y_pred == 1, 0, 1)


# 学習後のAUCの計算
auc = roc_auc_score(y, scores)
print(f"再学習後のAUC: {auc}")  


# ROC曲線の描画
fpr, tpr, thresholds = roc_curve(y, scores)
plt.plot(fpr, tpr, label=f'AUC = {auc:.2f}')
plt.plot([0, 1], [0, 1], linestyle='--', color='gray') # ランダム分類器のROC曲線
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend()
plt.show()


# 評価指標の出力
print(classification_report(y, y_pred))
print(confusion_matrix(y, y_pred))

Normal transactions: 284315
Fraudulent transactions: 492

 0.05689087 0.05509471 0.05349197 0.05068765 0.04702427 0.0474699
        nan        nan        nan        nan        nan        nan
 0.06238867 0.05513068 0.05286581 0.04851914 0.04944925 0.04942027
        nan        nan        nan        nan        nan        nan
 0.0542924  0.05505526 0.05861238 0.049081   0.05009604 0.04811162]
  warnings.warn(
Best parameters: {'contamination': 0.0017, 'max_features': 0.5, 'max_samples': 'auto', 'n_estimators': 50}
Best score: 0.06238867046341958
再学習後のAUC: 0.059203471358702825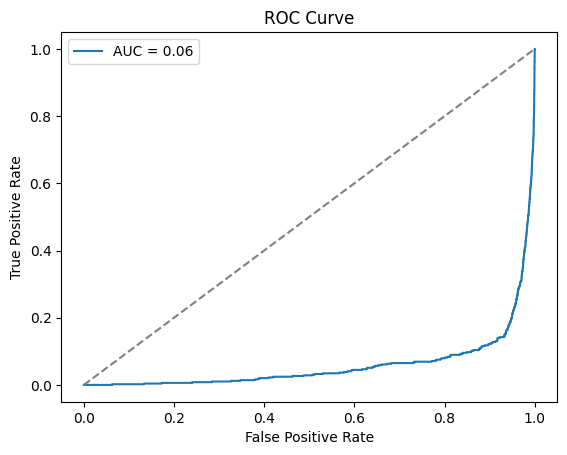

              precision    recall  f1-score   support

           0       1.00      1.00      1.00    284315
           1       0.18      0.17      0.18       492

    accuracy                           1.00    284807
   macro avg       0.59      0.59      0.59    284807
weighted avg       1.00      1.00      1.00    284807

[[283916    399]
 [   406     86]]

少しだけ改善されましたね。

モデルの注意点と応用

• データの不均衡：異常データが極端に少ないため、評価指標の選択に注意が必要。
• ハイパーパラメータの調整：contaminationやn_estimatorsなどのパラメータが結果に影響。
• スケーリングの重要性：特徴量のスケールが異なる場合、標準化が必要。

• 不正検出：金融取引や保険請求の不正行為の検出。
• 品質管理：製造業における異常製品の検出。
• サイバーセキュリティ：ネットワークトラフィックの異常検出。

学習の振り返りと次回予告

今回の講義では、次元削減と異常検知の重要な手法について学びました。主成分分析（PCA）は、データの主要な変動要素を抽出し、次元を減らして視覚的に表現するための手法で、線形構造のデータに適用されます。一方、t-SNEは非線形なデータの構造を保持しつつ低次元化する方法で、パラメータ調整や計算コストに注意が必要です。異常検知に使われるIsolation Forestは、データをランダムに分割して異常値を効率的に検出し、特にデータの不均衡やハイパーパラメータの調整が精度に影響します。これらの手法は、高次元データの解析や異常パターンの発見において非常に有用です。

次回の後編では、LDAによるテーマモデリングで文書データの潜在トピックを抽出し、オートエンコーダで高次元データを低次元に圧縮する方法を紹介します。これにより、Kaggleなどで複雑なデータ処理の力をさらに高められるでしょう。お楽しみに！