第7回の目標
第7回中編のブログでは、決定木とランダムフォレストを深く理解し、実践的に活用することを目指します。ただ単にアルゴリズムの仕組みを知るだけでなく、それぞれの特性や適用場面を意識しながら学習を進めることが重要です。
決定木では、不純度の概念や分岐の基準、過学習を防ぐための剪定手法を学び、ランダムフォレストでは決定木との違いやアンサンブル学習の強みを理解します。
また、実際のデータを用いた実装を通じて、モデルのパフォーマンスを評価し、より効果的な機械学習の適用方法を考察します。本ブログを通じて、アルゴリズムの選択理由を説明できる力を身につけ、機械学習を使いこなすための視点を養うことを意識して取り組んでいきます。
決定木 (Decision Tree)
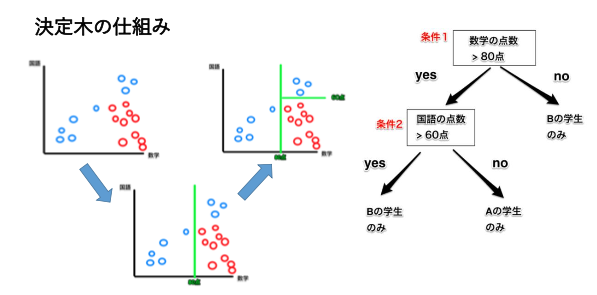
決定木は、データを条件に基づいて再帰的に分割し、最終的に予測を行うアルゴリズムで、特に視覚的で解釈しやすいモデルとして知られています。データを特定の特徴の条件に従って分類または回帰する際に、木構造を使って「決定を下す」という原理で設計されています。このため、特に非線形なデータでも高いパフォーマンスを発揮することがあり、解釈性の高さが多くの業界で重宝されています。
| 特徴 | 説明 |
|---|---|
| 直感的な構造 | 決定木は条件を順に分岐させていくツリー構造を持ち、各特徴の条件に基づき分類・予測を行います。 |
| 分類と回帰が可能 | 決定木は、分類問題ではクラスの予測、回帰問題では連続値の予測に対応しています。 |
| 解釈性が高い | データの分割条件が明示的に見えるため、モデルの決定過程がわかりやすく、可視化や説明がしやすいです。 |
| 過学習のリスク | 特に深い木の場合、訓練データに過度に適合してしまうリスクが高く、一般化性能が低下する可能性があります。 |
| 不純度の削減 | 分岐条件はデータの「不純度」を最小化するように選択され、各ノードが最大限に一貫したグループを形成します。 |
| 分割基準の多様性 | ジニ係数、エントロピー、平均二乗誤差などの指標を使ってノードの分割基準が設定されます。 |
| 計算効率 | 決定木はスケーラブルで、比較的少ない計算リソースで構築できるため、さまざまな規模のデータに適用可能です。 |
不純度の指標
決定木の分岐条件は、データの「不純度」が最も少なくなるように選ばれ、各ノードができるだけ同質なグループを形成するようにします。
ジニ不純度$G$:
クラス分類においてはデータがどれだけ純粋に分類されているかを評価します。ジニ不純度は次の式で計算されます。
$$G = \sum_{k=1}^{K} p(k)(1 – p(k))$$
- $pk$ はクラス $k$の確率です。
エントロピー $H$:
情報理論に基づき、不確実性の度合いを測定する指標です。エントロピーは次の式で計算されます。
$$H = -\sum_{k=1}^{K} p_k \log_2 p_k$$
分割基準
決定木は、ノードを分割する際に「情報利得(Information Gain)」を用いて不純度を最小化する特徴を選択します。情報利得は、親ノードと子ノードのエントロピーの差で計算され、次のように表されます。
情報利得(Information Gain):
$$IG = H_{\text{parent}} – \left( \frac{N_{\text{left}}}{N_{\text{total}}} H_{\text{left}} + \frac{N_{\text{right}}}{N_{\text{total}}} H_{\text{right}} \right)$$
- $H_\text{parent}$ は親ノードのエントロピー
- $H_\text{left}$ 左の子ノードのエントロピー
- $H_\text{right}$ は右の子ノードのエントロピー
- $N_\text{left}$, $N_\text{right}$ はそれぞれ左と右の子ノードのサンプル数
- $N_\text{total}$ は親ノードのサンプル数
分割基準として情報利得が最大となる特徴を選択し、データをその特徴に基づいて分割します。
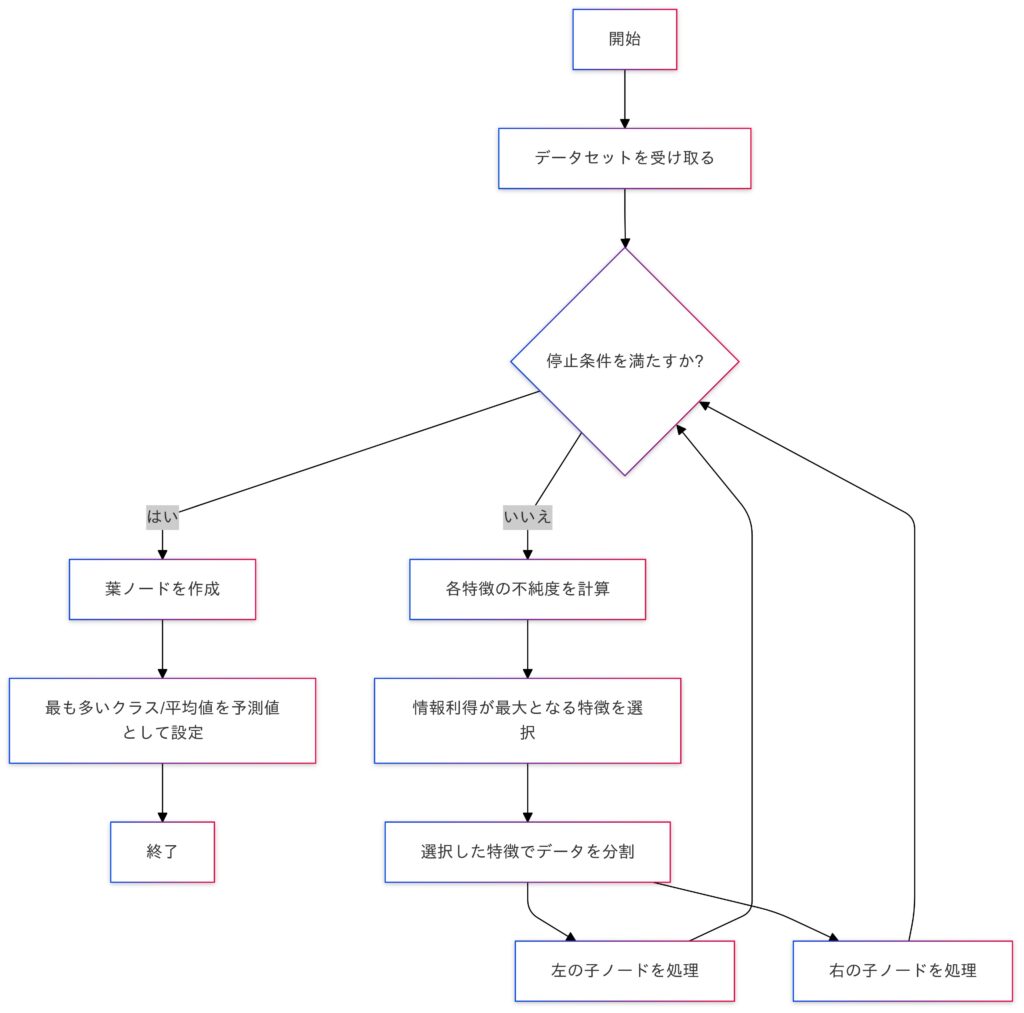
決定木のアルゴリズム
- 特徴選択:各特徴について不純度を計算し、情報利得が最大となる特徴を選択します。
- データ分割:選択した特徴を基に、データを枝分かれさせ、再帰的に分割していきます。
- 停止条件:分割を続けると、木が深くなり過学習のリスクが高まるため、以下の条件で分割を停止します。
- ノードのサンプル数が指定の最小値を下回る
- 不純度の低下が僅かで分割が不適切と判断される
- 予測:葉ノードに到達した場合、分類であれば最も多いクラスに、回帰であれば平均値を予測値として出力します。
決定木の応用
決定木は単独でも利用可能ですが、 ランダムフォレスト や 勾配ブースティング などのアンサンブル手法と組み合わせることで、過学習を抑えつつ高精度なモデルとして利用されるケースが多いです。
決定木の実装例(分類)
ライブラリのインポート:
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import pandas as pdデータの取得と前処理:
# データの読み込み
df = pd.read_csv('heart.csv')
# 特徴量とターゲットの分離
X = df.drop('num', axis=1)
y = df['num']
# 必要な前処理
label_encoders = {}
for column in X.select_dtypes(include={'object'}).columns: # object=文字列データ
le = LabelEncoder()
X[column] = le.fit_transform(X[column])
label_encoders[column]= le
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)モデルの学習と評価プロセス:
# モデルの定義
dt = DecisionTreeClassifier(max_depth=4, random_state=42)
# モデルの訓練
dt.fit(X_train, y_train)
# 予測
y_pred = dt.predict(X_test)
# 精度の評価
print("Accuracy:", accuracy_score(y_test, y_pred))
print(classification_report(y_test, y_pred))
print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))
# average='macro' を指定
print("Precision:", precision_score(y_test, y_pred, average='macro'))
print("Recall:", recall_score(y_test, y_pred, average='macro'))
print("F1-score:", f1_score(y_test, y_pred, average='macro'))Accuracy: 0.5706521739130435
precision recall f1-score support
0 0.73 0.89 0.80 75
1 0.45 0.67 0.54 54
2 0.00 0.00 0.00 25
3 0.22 0.08 0.11 26
4 0.00 0.00 0.00 4
accuracy 0.57 184
macro avg 0.28 0.33 0.29 184
weighted avg 0.46 0.57 0.50 184
Confusion Matrix:
[[67 7 1 0 0]
[15 36 1 2 0]
[ 6 15 0 4 0]
[ 3 20 1 2 0]
[ 1 2 0 1 0]]
Precision: 0.28009661835748795
Recall: 0.3273846153846154
F1-score: 0.2907988713404747決定木の可視化:
import matplotlib.pyplot as plt
plt.figure(figsize=(20,10))
class_names = ['Class 0', 'Class 1', 'Class 2', 'Class 3', 'Class 4'] # 実際のクラス名に合わせる
tree.plot_tree(dt, feature_names=X.columns, class_names=class_names, filled=True)
plt.show()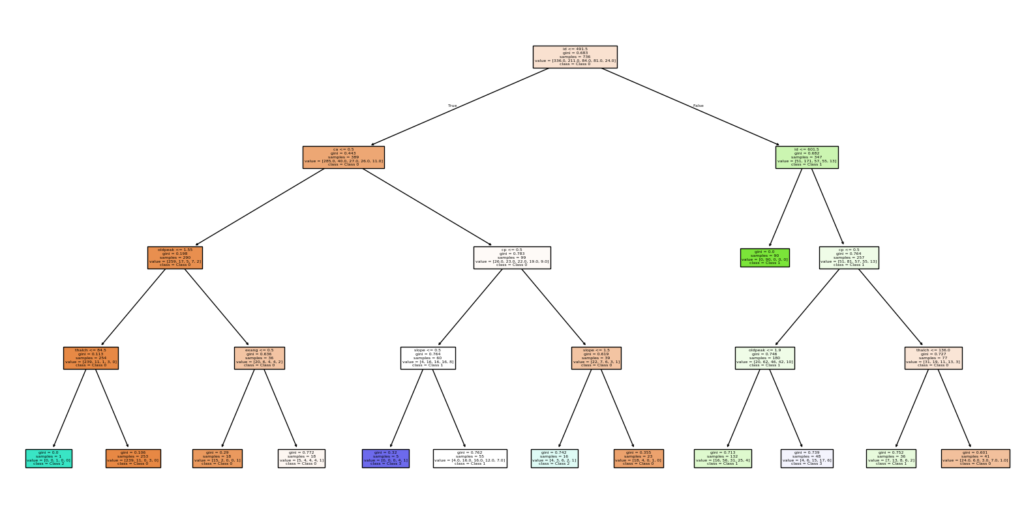
性能向上のための最適化(グリッドサーチによるハイパーパラメータチューニング):
from sklearn.model_selection import GridSearchCV
# チューニングするハイパーパラメータ
param_grid = {
'max_depth': [3, 4, 5, 6], # 決定木の最大深さ(デフォルト値:4)
'min_samples_split': [2, 5, 10], # ノードを分割するために必要な最小サンプル数
'min_samples_leaf': [1, 2, 4], # 葉ノードに含まれる必要のある最小サンプル数
'criterion': ['gini', 'entropy'], # どの特徴量で分割するかを決定する基準
'max_features': ['auto', 'sqrt', 'log2'], # 特徴量の数
'class_weight': ['balanced', None] # クラスの重み
}
# グリッドサーチ
grid_search = GridSearchCV(DecisionTreeClassifier(random_state=42), param_grid, cv=5)
grid_search.fit(X_train, y_train)
# 最適なパラメータ
print(grid_search.best_params_)
# 最適なモデル
best_dt = grid_search.best_estimator_
# 予測と評価
y_pred = best_dt.predict(X_test)
# 精度の評価
print("Accuracy:", accuracy_score(y_test, y_pred))
print(classification_report(y_test, y_pred))
print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))
# average='macro' を指定
print("Precision:", precision_score(y_test, y_pred, average='macro'))
print("Recall:", recall_score(y_test, y_pred, average='macro'))
print("F1-score:", f1_score(y_test, y_pred, average='macro')){'class_weight': None, 'criterion': 'gini', 'max_depth': 6, 'max_features': 'sqrt', 'min_samples_leaf': 4, 'min_samples_split': 10}
Accuracy: 0.5869565217391305
precision recall f1-score support
0 0.71 0.87 0.78 75
1 0.55 0.57 0.56 54
2 0.40 0.24 0.30 25
3 0.29 0.23 0.26 26
4 0.00 0.00 0.00 4
accuracy 0.59 184
macro avg 0.39 0.38 0.38 184
weighted avg 0.55 0.59 0.56 184
Confusion Matrix:
[[65 4 2 4 0]
[17 31 4 2 0]
[ 4 8 6 7 0]
[ 6 12 2 6 0]
[ 0 1 1 2 0]]
Precision: 0.3891614906832298
Recall: 0.3823019943019943
F1-score: 0.37947972526899776決定木の精度を向上させる方法
以下に、各方法を独立したテーブルに分けてまとめました。
1. 特徴量エンジニアリング
| 方法 | 説明 |
|---|---|
| 特徴量の組み合わせ | 既存の特徴量を掛け合わせたり比率を取ることで、新しい有力な特徴量を作成して精度向上を目指す |
| 新しい特徴量の作成 | ドメイン知識に基づいて独自の特徴量を追加(例:「年齢層」など) |
| 特徴量選択 | 重要な特徴量だけを選択し、不要なものを削減。フィルター法、ラッパー法などの手法を使用 |
2. データの前処理
| 方法 | 説明 |
|---|---|
| 欠損値処理 | 欠損値を削除または補完して、モデルの精度を維持 |
| 外れ値処理 | 外れ値を削除または変換して、モデルの安定性を確保 |
| データのスケーリング | 特徴量のスケールを標準化または正規化することで、スケールの違いを揃え、精度を向上 |
3. ハイパーパラメータのチューニング
| 方法 | 説明 |
|---|---|
| グリッドサーチ・ランダムサーチ | 幅広いパラメータの組み合わせを試行し、最適なパラメータを見つける |
| 交差検定 | データを分割して複数のモデルで検証し、モデルの汎化性能を向上 |
4. アンサンブル学習
| 方法 | 説明 |
|---|---|
| バギング | 複数の決定木の予測結果を平均化(例:ランダムフォレスト)し、モデルの精度を向上 |
| ブースティング | 誤分類サンプルに重みを付けて学習を繰り返す(例:勾配ブースティング)ことで、モデルの精度を向上 |
5. アルゴリズムの変更
| 方法 | 説明 |
|---|---|
| 他のアルゴリズムを試す | サポートベクターマシンやニューラルネットワークなど、決定木以外の手法を試すことでより高い精度を目指す |
6. データの追加
| 方法 | 説明 |
|---|---|
| データ量を増やす | より多くのデータを使用してモデルを学習することで、モデルの安定性と精度が向上する可能性がある |
決定木の剪定(Pruning)
剪定は、決定木の過学習を防ぐために、不要な枝やノードを削除して木を簡素化する手法です。大きく分けて2つの方法があり、以下のような特徴があります。
事前剪定(Pre-Pruning)
事前剪定は、木を作成する途中で条件を設けて、深くなりすぎないように分割を制限する方法です。
- 最大深さ(Max Depth):木の最大深さを制限する。
- 最小サンプル分割数(Min Samples Split):分割を行うノードに含まれるサンプルの最小数。
- 最小リーフサイズ(Min Leaf Size):葉ノードに含まれる最小サンプル数。
これらの条件を設定することで、成長中に早期停止が行われ、木が深くなりすぎないようにします。
これは先ほどのハイパーパラメータのグリッドサーチでパラメータを設定した方法と同じ方法になります。
# 事前剪定を行うモデルの定義
# (max_depth, min_samples_split, min_samples_leaf を設定)
# 決定木の最大深さ, ノードを分割するために必要な最小サンプル数, 葉ノードに含まれる必要のある最小サンプル数
dt = DecisionTreeClassifier(max_depth=3, min_samples_split=10, min_samples_leaf=5, random_state=42) 事後剪定(Post-Pruning)
事後剪定は、木を一度完全に成長させた後で、誤差と複雑度のバランスを取りながら不要な枝を削除する方法です。以下の手法がよく使われます。
コスト複雑度剪定(Cost Complexity Pruning):
コスト複雑度剪定では、次のような目的関数を使用して、モデルのコスト(誤差)と木の複雑さのバランスを取り、ペナルティが最も小さくなるように不要な枝を削除します。
$$C_\alpha(T) = R(T) + \alpha \times \text{size}(T)$$
ここで、$R(T)$ はモデルの誤差 $α$ はペナルティを調整するパラメータ、$\text{size}(T)$ は木のサイズ(ノード数)です。小さな誤差かつ簡素な木を目指すために、剪定を行います。
# モデルの定義(一旦、事前剪定なしで作成)
dt = DecisionTreeClassifier(random_state=42)
# モデルの訓練
dt.fit(X_train, y_train)
# Cost Complexity Pruningで最適なalphaを選択
path = dt.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities
# 各alphaで剪定した木を作成し、最もパフォーマンスの良いalphaを選択
models = [DecisionTreeClassifier(ccp_alpha=alpha, random_state=42).fit(X_train, y_train) for alpha in ccp_alphas]
# 交差検定で最適なalphaを選択
# ここでは、簡略化のため、訓練データの一部を検証データとして使用
X_train_sub, X_valid, y_train_sub, y_valid = train_test_split(X_train, y_train, test_size=0.2, random_state=42)
train_scores = [model.score(X_train_sub, y_train_sub) for model in models]
valid_scores = [model.score(X_valid, y_valid) for model in models]
best_alpha_index = valid_scores.index(max(valid_scores))
best_alpha = ccp_alphas[best_alpha_index]
# 最適なalphaでモデルを再訓練
best_dt = DecisionTreeClassifier(ccp_alpha=best_alpha, random_state=42).fit(X_train, y_train)
# 予測
y_pred = best_dt.predict(X_test)
# 精度の評価
print("Accuracy:", accuracy_score(y_test, y_pred))
print(classification_report(y_test, y_pred))
print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))
# average='macro' を指定
print("Precision:", precision_score(y_test, y_pred, average='macro'))
print("Recall:", recall_score(y_test, y_pred, average='macro'))
print("F1-score:", f1_score(y_test, y_pred, average='macro'))
plt.figure(figsize=(20,10))
class_names = ['Class 0', 'Class 1', 'Class 2', 'Class 3', 'Class 4'] # 実際のクラス名に合わせる
tree.plot_tree(best_dt, feature_names=X.columns, class_names=class_names, filled=True)
plt.show() Accuracy: 0.5543478260869565
precision recall f1-score support
0 0.70 0.87 0.77 75
1 0.61 0.50 0.55 54
2 0.21 0.12 0.15 25
3 0.25 0.23 0.24 26
4 0.11 0.25 0.15 4
accuracy 0.55 184
macro avg 0.38 0.39 0.37 184
weighted avg 0.53 0.55 0.54 184
Confusion Matrix:
[[65 4 1 3 2]
[14 27 6 6 1]
[ 7 5 3 8 2]
[ 7 8 2 6 3]
[ 0 0 2 1 1]]
Precision: 0.3775915840431969
Recall: 0.39348717948717954
F1-score: 0.37450444793301935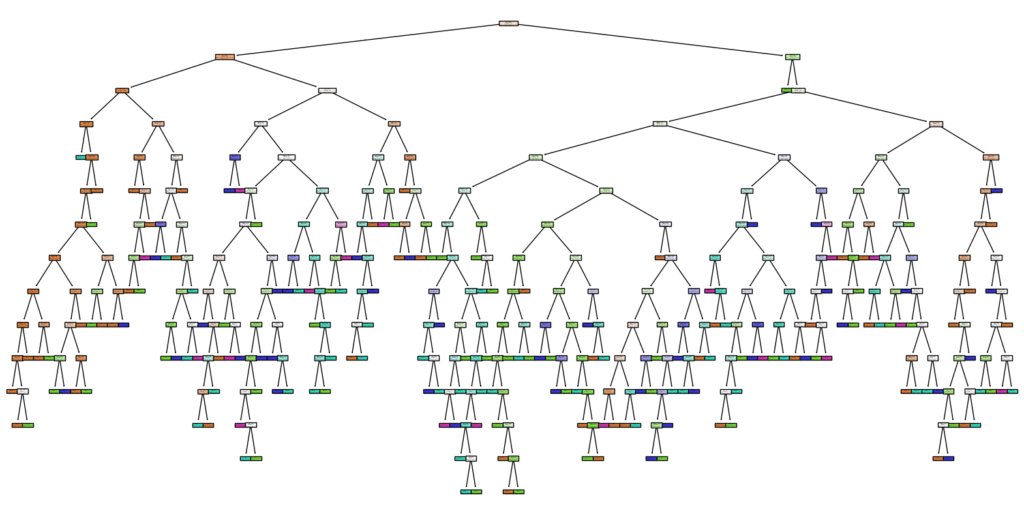
精度が向上する可能性があるケース:
結果的に精度は下がってしまいましたが、事後剪定はモデルが過学習などを起こしている場合や複雑なモデルである際に有効です。
精度が向上しない、または低下する可能性があるケース:
最適な ccp_alpha の選択は木の複雑さと誤差のバランスを取り精度向上に役立ちますが、すでに適切な複雑さのモデルや不適切な ccp_alpha の選択は、重要な情報を失い精度を低下させるリスクがあります。
精度向上のためのポイント:
最適な ccp_alpha を選択するには、グリッドサーチや交差検定を用いて訓練データと検証データで評価し、データセットやタスクに適した剪定方法を選ぶことで、過学習を防ぎ、汎化性能の高いモデルを構築することが重要です。
決定木(回帰分析)
次は決定木における回帰分析の手法の実装を行います。先ほど説明した事前剪定と事後剪定を取り入れて説明してみます。
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import pandas as pd
import matplotlib.pyplot as plt
# データの読み込み (例として、ボストン住宅価格データセットを使用)
from sklearn.datasets import fetch_california_housing
data = fetch_california_housing()
X, y = data.data, data.target
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 事前剪定を行うモデルの定義
# (max_depth, min_samples_split, min_samples_leaf を設定)
model = DecisionTreeRegressor(max_depth=3, min_samples_split=10, min_samples_leaf=5, random_state=42)
# モデルの訓練
model.fit(X_train, y_train)
# 予測
y_pred = model.predict(X_test)
# 評価指標 (RMSE, R^2)
rmse = mean_squared_error(y_test, y_pred, squared=False)
r2 = r2_score(y_test, y_pred)
print(f"RMSE: {rmse}")
print(f"R^2: {r2}")
# 決定木の可視化 (複雑な場合は省略)
# plt.figure(figsize=(15, 10))
# tree.plot_tree(model, feature_names=boston.feature_names, filled=True)
# plt.show()
# 決定木の可視化
plt.figure(figsize=(15, 10))
tree.plot_tree(model, feature_names=data.feature_names, filled=True)
plt.show() RMSE: 0.8015054466605727
R^2: 0.5097629887358219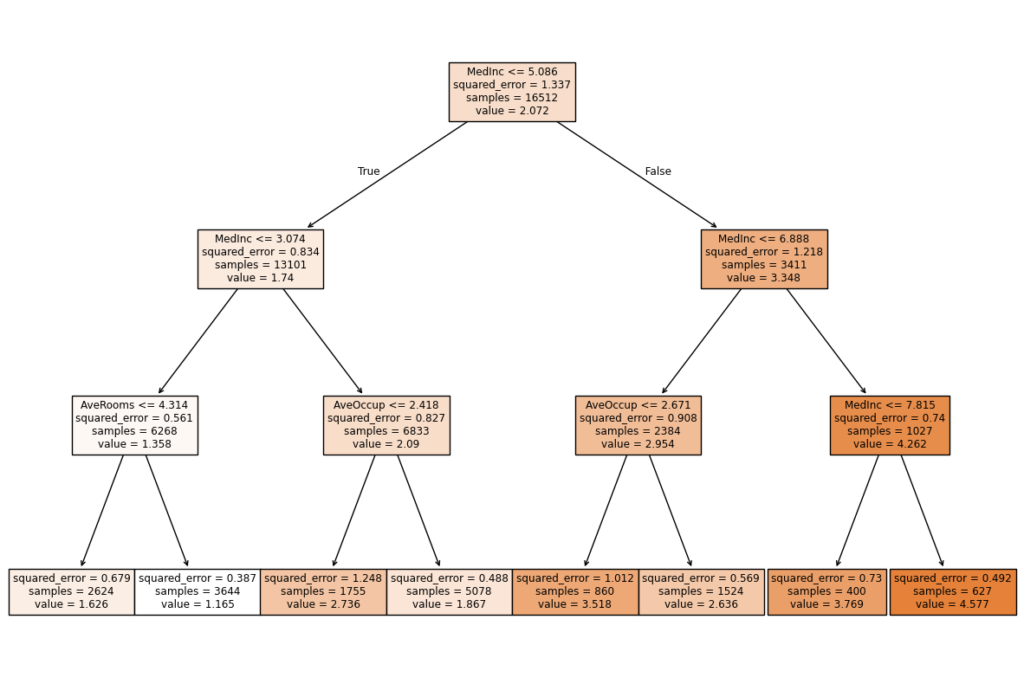
RMSEを使うメリット:
RMSEは、目的変数と同じ単位で表されるため、結果の解釈が容易です。例えば、住宅価格の予測であれば、RMSEは価格の単位(円など)で表されます。
事後剪定と最適化を取り入れた精度向上の方法例:
# ハイパーパラメータのグリッドサーチ用設定
param_grid = {
'max_depth': [3, 4, 5, 6],
'min_samples_split': [2, 5, 10],
'min_samples_leaf': [1, 2, 4],
'ccp_alpha': [0.0, 0.01, 0.1, 0.2] # 事後剪定のためのパラメータ
}
# グリッドサーチの設定
grid_search = GridSearchCV(DecisionTreeRegressor(random_state=42), param_grid, cv=5)
grid_search.fit(X_train, y_train)
# 最適なモデル
best_model = grid_search.best_estimator_
# 予測
y_pred = best_model.predict(X_test)
# 評価指標 (RMSE, R^2)
rmse = mean_squared_error(y_test, y_pred, squared=False)
r2 = r2_score(y_test, y_pred)
print(f"Best Parameters: {grid_search.best_params_}")
print(f"RMSE: {rmse}")
print(f"R^2: {r2}")Best Parameters: {'ccp_alpha': 0.0, 'max_depth': 6, 'min_samples_leaf': 2, 'min_samples_split': 5}
RMSE: 0.7043171862677146
R^2: 0.6214443680491355RMSEが下がり、R²が上がっている場合、モデルの予測精度が向上していると解釈できます。これは、モデルがデータの変動をよりよく捉え、より正確な予測を行えるようになったことを示しています。また過学習のリスクが低下している可能性もあるという解釈ができます。
ランダムフォレスト (Random Forest)
ランダムフォレスト(Random Forest)は、複数の決定木を組み合わせて予測を行うアンサンブル学習の手法です。各決定木が独立したサブサンプルで学習するため、バギング(Bootstrap Aggregating)を活用し、過学習を抑えつつ精度の向上を図ります。
ランダムフォレストの手順:
1. バギング(Bootstrap Aggregating):
- データのサブセット(ブートストラップサンプル)をランダムに抽出し、各決定木はこのサブセットで学習を行います。
- 各決定木は、全体のデータセットではなく、異なるサブセットで訓練されます。このため、個々の決定木が全体データに対して依存度が低くなり、汎化性能が向上します。
2. 特徴量のランダム選択:
- 各ノードで分割を行う際に、ランダムに選ばれた特徴量の中から最も分割の効果が高いものを使用します。
$$\text{S_F} = \arg \max_{\text{f} \in \text{rf}} \text{I_G}{f}$$
- $I_G({f})$ = 分割に使われる基準(ジニ不純度やエントロピー)に基づく
- $S_F = \text{Split Feature}$
- $f = \text{feature}$
- $rf = \text{random feature}$
3. 予測の集約
- 最終的な予測は、複数の決定木の予測結果を集約することで行います。
分類問題:各決定木の予測結果を多数決(投票)で集約。
$$\hat{y} = \arg \max_{c} \sum_{i=1}^{n} I(T_i(x) = c)$$
- $T_i(x)$ は木 $i$ の予測
- $c$ はクラスラベル
- $I$ はインジケータ関数
回帰問題:各決定木の予測値の平均を取ります。
$$\hat{y} = \frac{1}{n} \sum_{i=1}^{n} T_i(x)$$
ランダムフォレストの実装(分類問題)
それでは、乳がんの診断のデータセットを用いて説明します。
目的関数であるdiagnosisにはMとBがあります。
M: Malignant(悪性)
悪性腫瘍を示し、がんであることを意味します。この場合、腫瘍は周囲の組織に浸潤し、転移する可能性があります。
B: Benign(良性)
良性腫瘍を示し、がんではないことを意味します。良性腫瘍は通常、周囲の組織に浸潤せず、転移することはありません。
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
import pandas as pd
# データの読み込み
df = pd.read_csv('breast_cancer.csv')
# 特徴量とターゲットの分離
X = df.drop(['id', 'diagnosis'], axis=1)
y = df['diagnosis'].map({'M': 1, 'B': 0})
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# モデルの定義
# n_estimators=100:アンサンブルモデルにおける決定木の数の指定
# max_depth=5:各決定木の深さを指定
# random_state=42:乱数生成のシード値を指定
rf = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=42)
# モデルの訓練
rf.fit(X_train, y_train)
# 予測
y_pred = rf.predict(X_test)
# 精度の評価
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')Accuracy: 0.96ランダムフォレストから1本の決定木を可視化:
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
# ランダムフォレストから1本の決定木を可視化
plt.figure(figsize=(15, 10))
plot_tree(rf.estimators_[0], feature_names=X.columns, filled=True)
plt.title("Random Forest - Decision Tree Visualization")
plt.show()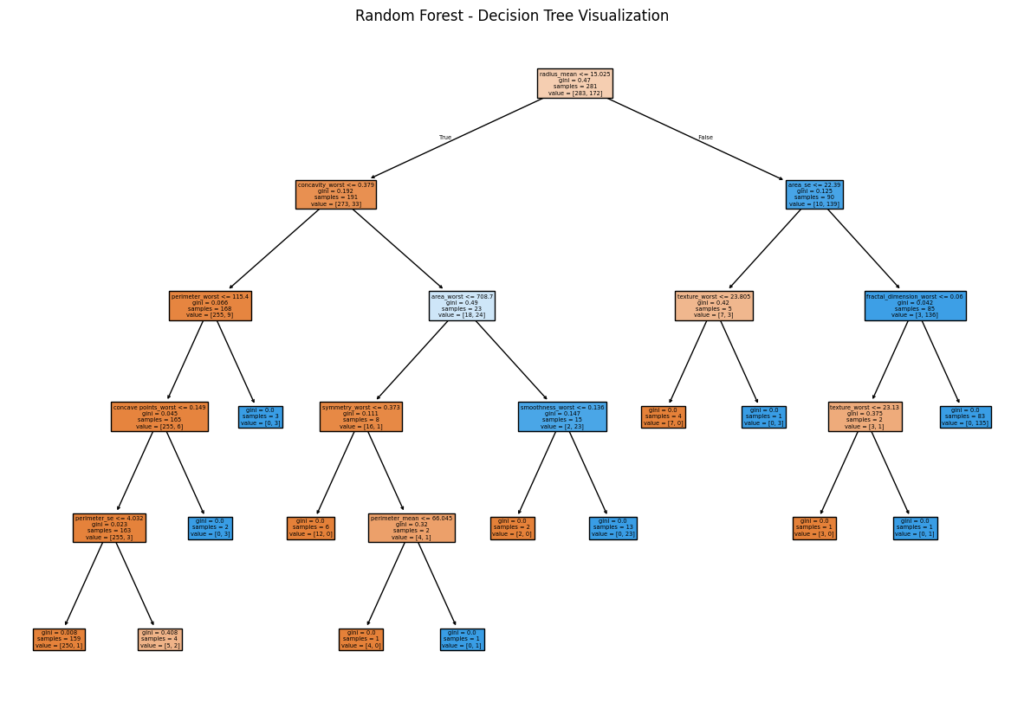
特徴量の重要度を可視化:
import numpy as np
# 特徴量の重要度を取得
importances = rf.feature_importances_
# 特徴量の重要度を可視化
plt.figure(figsize=(10, 6))
indices = np.argsort(importances)[::-1]
plt.title("Feature Importances")
plt.bar(range(X.shape[1]), importances[indices], align="center")
plt.xticks(range(X.shape[1]), X.columns[indices], rotation=90)
plt.xlim([-1, X.shape[1]])
plt.show()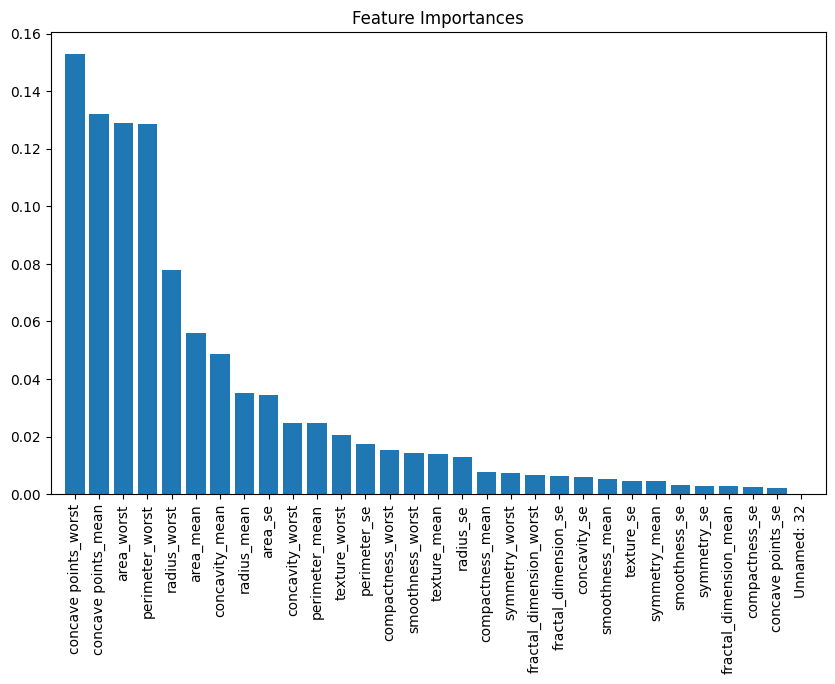
- ランダムフォレストモデルの一部である決定木を可視化することで、モデルがどのようにデータを分割しているかを理解することができます。
- 各特徴量がモデルの予測にどれだけ寄与しているかを示すことで、どの特徴量が乳がんの診断において重要であるかを把握できます。
モデルの性能を向上させるためには?
大きくは決定木と違いはないのですが、ランダムフォレスト特有のハイパーパラメータやアプローチの改善を図ることでモデルの性能を向上させることが可能です。
ランダムフォレストの実装(分類問題)
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.datasets import fetch_california_housing
import pandas as pd
import matplotlib.pyplot as plt
# データの読み込み (カリフォルニア州住宅価格データセット)
data = fetch_california_housing()
X, y = data.data, data.target
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# ランダムフォレスト回帰モデルの定義
rf_model = RandomForestRegressor(n_estimators=100, max_depth=5, random_state=42)
# モデルの訓練
rf_model.fit(X_train, y_train)
# 予測
y_pred = rf_model.predict(X_test)
# 評価指標 (RMSE, R^2)
rmse = mean_squared_error(y_test, y_pred, squared=False)
r2 = r2_score(y_test, y_pred)
print(f"RMSE: {rmse:.2f}")
print(f"R^2: {r2:.2f}")
# 特徴量の重要度を可視化
importances = rf_model.feature_importances_
indices = np.argsort(importances)[::-1]
plt.figure(figsize=(10, 6))
plt.title("Feature Importances")
plt.bar(range(X.shape[1]), importances[indices], align="center")
plt.xticks(range(X.shape[1]), [data.feature_names[i] for i in indices], rotation=90) # リスト内包表記を使用
plt.xlim([-1, X.shape[1]])
plt.show()RMSE: 0.68
R^2: 0.65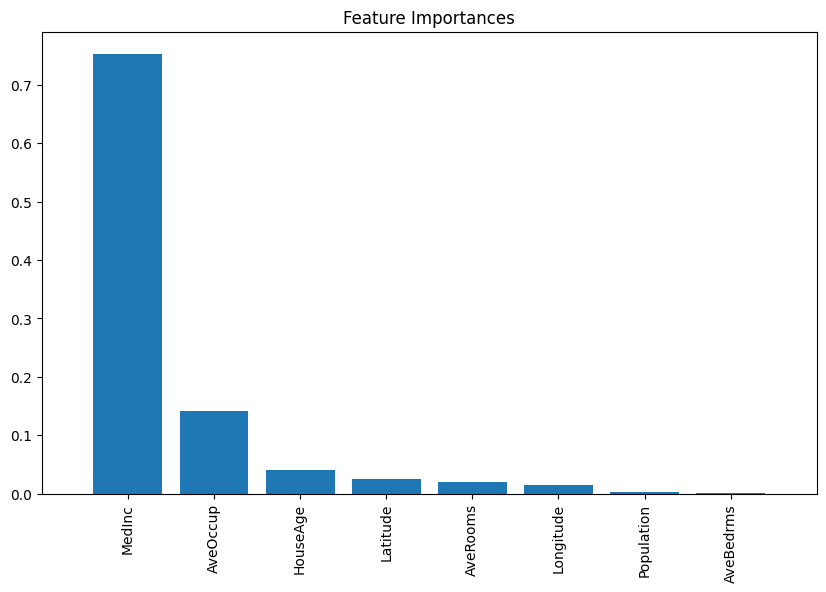
モデルの精度向上の例(特徴量の選択とデータの前処理):
# 特徴量の選択 (例: 特徴量の重要度を基に選択)
rf_model = RandomForestRegressor(n_estimators=100, max_depth=5, random_state=42)
rf_model.fit(X_train, y_train)
importances = rf_model.feature_importances_
indices = np.argsort(importances)[::-1]
# 重要度が高い上位5つの特徴量を選択
top_features = indices[:5]
X_train_selected = X_train[:, top_features]
X_test_selected = X_test[:, top_features]
# 新しいモデルの訓練
rf_model_selected = RandomForestRegressor(n_estimators=100, max_depth=5, random_state=42)
rf_model_selected.fit(X_train_selected, y_train)
# 予測
y_pred_selected = rf_model_selected.predict(X_test_selected)
# 評価指標 (RMSE, R^2)
rmse_selected = mean_squared_error(y_test, y_pred_selected, squared=False)
r2_selected = r2_score(y_test, y_pred_selected)
print(f"RMSE (Selected Features): {rmse_selected:.2f}")
print(f"R^2 (Selected Features): {r2_selected:.2f}")グリッドサーチ以外にも、モデルの精度を向上させるためのさまざまな手法があります。特徴量エンジニアリング、データの前処理、アンサンブル手法の利用、モデルの複雑さの調整、クロスバリデーションの利用、より多くのデータを使用することなどが有効です。これらの手法を組み合わせて試すことで、モデルの性能を向上させることができます。
決定木とランダムフォレストの違い
今回は決定木とランダムフォレストでほぼ同じようなアルゴリズムの内容ではありましたが、使う場合に明確な違いがあり、それぞれのメリット、デメリットがあるため、やはり使い分けは必要であると感じました。決定木において精度を向上したモデルをランダムフォレストに応用する方法など、使い方は様々ですが、決定木の場合は過学習のリスクがあり、使う際は十分に気をつけなくてはなりません。
以下に決定木とランダムフォレストの違いをまとめておきましたので是非ご活用ください。
特徴・利点・欠点:
| 項目 | 決定木 | ランダムフォレスト |
|---|---|---|
| 基本構造 | 単一の木構造でデータを分割し、予測を行う。 | 複数の決定木を組み合わせて予測を行うアンサンブル手法。 |
| 利点 | ・解釈が容易で直感的に理解しやすい ・特定のデータセットに対して良好な性能を示すことがある | ・過学習のリスクが低く、より安定した予測が可能 ・ノイズの多いデータや複雑なパターンにも効果的 |
| 欠点 | ・過学習しやすく、特に深い木構造で訓練データに適合しすぎるリスクがある ・ノイズや外れ値に敏感 | ・ 訓練と予測に時間がかかることがある ・ モデルの解釈が複雑で、個々の決定木の判断基準が分かりにくい |
| 性能向上の工夫 | ・適切な剪定やハイパーパラメータの調整で、過学習を抑えつつ精度向上が可能 ・サンプルや特徴量を増やし性能を改善 | ・アンサンブルのためのバギングと特徴量のランダム選択により、個々の決定木の弱点を補う ・ 各決定木の精度向上で全体の性能向上も期待できる |
| 適用シーン | ・単体での解釈性が求められる場合 ・小規模データで特徴が明確なデータセットに適応 | ・より複雑なデータセット、ノイズが多い場合に有効 ・ 過学習を抑え、汎化性能が重視されるケース |
| 結論 | 決定木はシンプルで解釈しやすいが、過学習しやすいため注意が必要。 | ランダムフォレストは決定木の弱点を補い、より汎化性能の高い安定した予測が可能 |
学習の狙い
この回では、決定木とランダムフォレストの基本原理をしっかりと理解し、単体のアルゴリズムとアンサンブル手法の違い、そしてそれぞれのアルゴリズムが得意とするデータ構造や適用場面を学びます。決定木が提供する直感的な解釈性やデータの分岐処理に対する利点、ランダムフォレストが多数の決定木を組み合わせることで得られる汎化性能の向上と過学習の抑制を比較し、それぞれの長所と短所を把握します。
この理解を通じて、単純なツリー構造が適している場面と、複雑なアンサンブルが有効な場面を見極め、実際のデータやタスクに最も適したモデル選択ができるようになることを目指します。また、特徴量の重要度評価などランダムフォレスト特有の機能についても学ぶことで、データ解釈におけるアルゴリズムの有用性を身につけることが期待されます。
次回予告
次回、第7回:教師あり学習の基礎と代表的なアルゴリズム(後編)では、機械学習における分類手法の中でもより高度なモデルであるサポートベクターマシン(SVM)と多層パーセプトロン(MLP)を取り上げます。これらの手法は非線形問題への対応力が高く、特に複雑なデータパターンに対する解決策として注目されています。
これまで学んだ決定木やランダムフォレストと異なり、SVMは最大マージンによる分類、MLPは層を重ねたネットワーク構造を用いるため、データの「分離性」や「層ごとの特徴抽出」という概念を理解することが重要です。SVMではカーネルによる非線形変換の原理、MLPでは各層を通じて行われる非線形変換と学習プロセスについて深掘りし、どのようにして複雑な分類を可能にするのかを学んでいきます。
これらのアルゴリズムを学ぶことで、より柔軟かつ高度なモデル選択ができるように準備を整えていきましょう。
それでは次回もお楽しみに!



コメント