概要
金融市場のデータ分析において、クラスタリングは銘柄のグループ分けや市場レジームの特定に強力なツールです。中でも階層クラスタリングは、単にデータを分割するだけでなく、その背後にある「構造」を可視化し、より深い洞察を得るために極めて有効な手法です。
本記事では、一般的なクラスタリング手法との違いを明確にしながら、階層クラスタリングを金融市場取引で実践的に活用する方法と、その注意点について解説します。
◾️クラスタリングについての基礎知識については下記ブログを参照してください。
K-meansとの違い:なぜ階層クラスタリングを選ぶのか?
クラスタリングの代表的な手法にK-means法があります。K-meansは、事前に指定したクラスタ数(k)に基づき、データを高速に分類することに長けています。しかし、金融市場のように複雑で、最適な分類数が不明確な対象を分析する際には、いくつかの課題があります。
- K-means:
- クラスタ数を事前に決める必要がある。クラスター間の関係性は示されない。
- 階層クラスタリング:
- クラスタ数を事前に決める必要がない。データの類似度に基づき、樹形図(デンドログラム)を作成し、データの階層構造そのものを明らかにする。
階層クラスタリングが金融分析で特に有効なのは、このデンドログラムにあります。デンドログラムは、どのデータ点が互いに近いのか、そしてそれらがどのような順序で、どれくらいの「距離」を保ちながら、より大きなグループを形成していくのかを可視化します。これにより、単なる分類結果だけでなく、データセット全体の構造的な関係性を直感的に理解できるのです。
階層クラスタリングの具体的な金融市場取引への活用法
銘柄のグルーピングとポートフォリオ構築
デンドログラムを用いることで、従来のセクター分類では見えなかった銘柄間の真の関係性が明らかになります。
- 構造に基づいた分散投資:
- ポートフォリオを構築する際、デンドログラム上で物理的に離れた位置にある銘柄を組み合わせることで、より本質的な分散効果が期待できます。
- 階層構造の理解:
- 例えば、「半導体セクター」という大きな括りの中でも、デンドログラムを見れば「製造装置メーカー群」と「設計専門企業群」が明確に異なるサブグループを形成していることや、それらの間の距離感を把握できます。
- ペアトレード候補の発見:
- デンドログラムの最も低い位置で結合している(=最も距離が近い)銘柄ペアは、統計的に非常に強い相関を持つことを意味し、有力なペアトレードの候補となります。
市場レジームの階層的分析
市場の状況(レジーム)を「平常時」「高ボラティリティ時」「暴落時」などに分類する際、階層クラスタリングはそれらの関係性を明らかにします。
- 状態遷移の理解:
- デンドログラムは、「高ボラティリティ時」が「平常時」よりも「暴落時」に性質として近い(=距離が近い)ことを示唆してくれるかもしれません。これは、市場の状態遷移確率をモデル化する上で重要な洞察となります。
- 戦略選択とリスク管理:
- 現在の市場がデンドログラム上のどの位置にあるかを特定し、その親クラスタや兄弟クラスタの性質を考慮することで、より精緻な戦略選択やリスク管理の調整が可能になります。
ニュースセンチメントと市場イベントの階層分析
ニュース記事やSNS投稿をベクトル化し、階層クラスタリングを適用することで、情報の伝播構造を分析できます。
- センチメントの深層構造:
- 個別のニュースが、より大きなテーマやイベントのクラスターにどのように属しているかを階層で捉えることができます。例えば、「A社のポジティブな決算発表」というニュースが、「ハイテク株の業績回復」というクラスターに属し、さらにそれが「マクロ経済の楽観ムード」という上位クラスターとどう関連しているかを分析できます。
- イベント連鎖分析:
- ある地政学リスクの発生(ニュースA)が、次にどのトピック(ニュースB)と結びつき、市場に影響を与えていくか、といったイベントの連鎖反応をデンドログラム上で追跡する手がかりを得られます。
トレーディングボットの行動パターンの階層的分類
高頻度取引(HFT)などで活動するボットの行動様式を階層的に分類することで、競合の戦略をより深く理解できます。
- 戦略タイプの詳細な理解:
- 例えば、「マーケットメイク戦略」という大きなクラスタの中でも、デンドログラムを見れば「スプレッドを広く取るタイプ」と「タイトに設定するタイプ」といったサブグループの存在が明らかになるかもしれません。
- 競合戦略の深層分析:
- 一見すると異なる振る舞いをしている2つのボットが、デンドログラム上では「裁定取引」という共通の親クラスタから派生した、異なる亜種である可能性を発見するなど、競合の戦略ポートフォリオをより解像度高く分析できます。
応用のための参考論文
銘柄のグルーピングとポートフォリオ最適化
- 論文タイトル:
- Building Diversified Portfolios that Outperform Out-of-Sample(アウトオブサンプルで優れたパフォーマンスを発揮する分散ポートフォリオの構築)
- 著者:Marcos Lopez de Prado
- URL:https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2708678
- ブログとの関連性: この論文は、階層クラスタリングをポートフォリオ最適化に応用した画期的な手法である「階層的リスクパリティ(Hierarchical Risk Parity, HRP)」を提案した独創的な研究の一つです。ブログで解説されている「デンドログラムに基づき、構造を理解してポートフォリオを構築する」というアイデアを、具体的なアルゴリズムとして示した金字塔的な論文であり、引用することで専門的な深みが格段に増します。
- 論文要約:
- 本論文は、伝統的なポートフォリオ最適化手法、特にマルコビッツのCLAが抱える「マルコビッツの呪い」に起因する不安定性、集中、アウトオブサンプルでのアンダーパフォーマンスといった問題を指摘します。これらの問題は、共分散行列の逆行列計算や、投資間の「完全グラフ」的な関係性モデルに起因すると分析。そこで、著者らは「階層的リスクパリティ(HRP)」という新しいポートフォリオ構築手法を提案します。HRPは、共分散行列の逆行列計算や正定値性を必要とせず、グラフ理論と機械学習(ツリークラスタリング、準対角化、再帰的二分割)を応用します。HRPは、投資間の「階層構造」と「関係性」を重視し、デンドログラムを通じて可視化することで、より頑健で、アウトサンプルでの分散が低く、リスク調整後リターンが高いポートフォリオを構築できることをモンテカルロシミュレーションで示しました。これにより、安定したポートフォリオ構築への新たな道が開かれます。
HRP(階層的リスク・パリティ)とは?
従来のリスク・パリティは、資産ごとのリスク寄与を均等にすることを目指しますが、相関性の高い資産が多いと、実質的にリスクが集中してしまう問題があります。HRP(階層的リスク・パリティ)はこの課題に対処するため、まず資産間の相関関係に基づいてクラスタリングを行い、似た動きをする資産をグループ化します。その後、階層構造に従ってリスクを段階的に分配し、グループ間・グループ内の両方でバランスのとれた配分を実現します。これにより、ポートフォリオ全体の構造的なリスク分散が可能となり、市場の急変動時でもより安定した運用が期待できます。HRPは、単なる数値最適化ではなく、相関構造を視覚的・構造的に捉える点でも優れており、実務での説明性や堅牢性の高さから注目されています。
論文の実装例
この実装では、論文で提案された独自の距離尺度を忠実に再現し、seaborn.clustermapを用いた「準対角化」によって、複雑な理論を視覚的にわかりやすく表現しています。さらに、yfinanceで実際の金融データを取得し、pandasやscipyなどの標準ライブラリを活用することで、理論と実データの橋渡しを実現しています。コードの構造も整理されており、可読性が高く、視覚的にも理解を深めやすい工夫が随所に見られます。
import yfinance as yf
import pandas as pd
import numpy as np
import scipy.cluster.hierarchy as sch
import matplotlib.pyplot as plt
import seaborn as sns
# ステップ1 & 2: 金融データの取得と準備
# ----------------------------------------------------
# 多様なセクターから銘柄を選択
# (例: テック, 金融, 消費財, ヘルスケア, エネルギー, 国際インデックス)
tickers = ['AAPL', 'MSFT', 'JPM', 'PG', 'JNJ', 'XOM', 'EWJ', 'GLD']
start_date = '2020-01-01'
end_date = '2023-12-31'
# yfinanceを使って株価データを取得
data = yf.download(tickers, start=start_date, end=end_date)['Close']
# 日次リターンを計算
returns = data.pct_change().dropna()
print("取得したデータのリターン(最初の5行):")
print(returns.head())
# ステップ3: 相関行列と距離行列の計算
# ----------------------------------------------------
# リターンから相関行列を計算
corr_matrix = returns.corr()
# 論文の式(A.1)に基づいて相関を距離に変換
# d(i,j) = sqrt(0.5 * (1 - rho(i,j)))
# この式は、相関が1のときに距離が0、相関が-1のときに距離が1になる(HRPのステージ1: ツリークラスタリングの準備)
dist_matrix = np.sqrt((1 - corr_matrix) / 2)
print("\n相関行列:")
print(corr_matrix)
print("\n距離行列:")
print(dist_matrix)
# ステップ4: 階層クラスタリングの実行
# ----------------------------------------------------
# 距離行列から連結行列を計算
# 'ward'法は、クラスター内の分散を最小化するようにクラスターを併合していく手法で、一般的によく使われます。(HRPのステージ1: ツリークラスタリングの核心)
linkage_matrix = sch.linkage(dist_matrix, method='ward')
print("\n連結行列 (Linkage Matrix):")
# 各行は [クラスターID1, クラスターID2, 距離, 新クラスターの要素数] を示す
print(linkage_matrix)
# ステップ5: 可視化
# ----------------------------------------------------
# 5.1: デンドログラムのプロット(HRPのステージ1: ツリークラスタリングの可視化)
plt.figure(figsize=(12, 6))
plt.title('Hierarchical Clustering Dendrogram', fontsize=16)
plt.xlabel('Assets', fontsize=12)
plt.ylabel('Distance', fontsize=12)
# デンドログラムをプロット
sch.dendrogram(linkage_matrix, labels=corr_matrix.index, leaf_rotation=90)
plt.tight_layout()
plt.show()
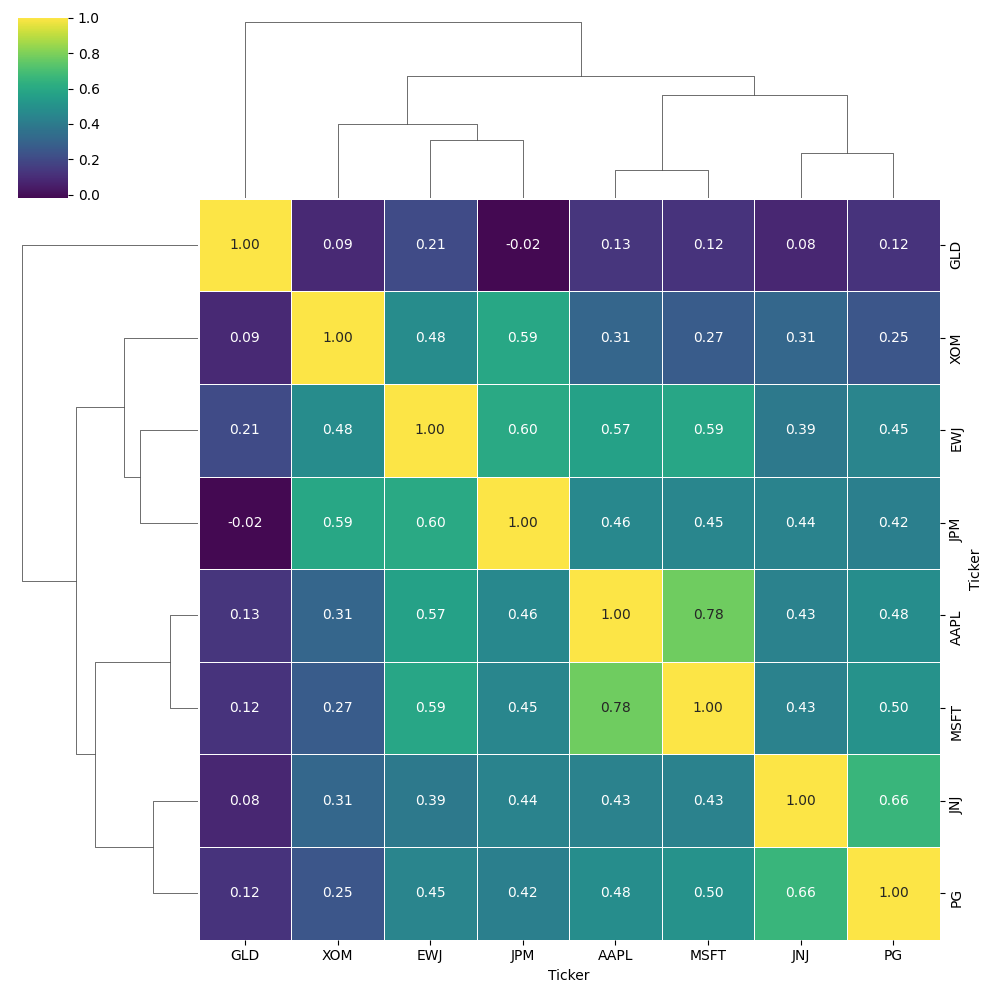
# 5.2: クラスタリングされたヒートマップ (ステージ2: 準対角化の可視化)
# seabornのclustermapは、クラスタリングとヒートマップのプロットを同時に行ってくれる便利な関数です。
# これにより、論文で述べられている「準対角化」された行列を直感的に理解できます。
plt.figure(figsize=(10, 10))
sns.clustermap(corr_matrix,
method='ward', # クラスタリング手法
cmap='viridis', # カラーマップ
annot=True, # 相関係数を表示
fmt=".2f", # 小数点以下2桁で表示
linewidths=.5)
plt.suptitle('Quasi-Diagonalized Correlation Matrix (Clustered Heatmap)', fontsize=16, y=1.02)
plt.show()- デンドログラム:
- この図は、論文の「ステージ1:ツリークラスタリング」の結果を示しており、資産同士の相関関係を階層的に視覚化しています。どの銘柄が強く関連し、どのようにクラスターを形成・統合していくかが一目で分かり、従来の完全グラフでは捉えにくかった構造的な関係性を直感的に理解できます。階層的なリスク管理を行う上で、非常に有効な可視化手法です。

- クラスタリングされたヒートマップ:
- この図は論文の「ステージ2:準対角化」の考え方を視覚的に表現したもので、相関行列がクラスタリング結果に基づいて並べ替えられています。相関の高い銘柄群が対角線上にブロック状に現れ、リスクの集中や分散の状況を直感的に把握できます。従来手法が見落としがちな相関構造を、HRPが構造的に活用していることを明確に示しています。
取得したデータのリターン(最初の5行):
Ticker AAPL EWJ ... PG XOM
Date ...
2020-01-03 -0.009722 -0.011026 ... -0.006725 -0.008039
2020-01-06 0.007968 0.003547 ... 0.001387 0.007678
2020-01-07 -0.004703 0.001683 ... -0.006191 -0.008184
2020-01-08 0.016086 0.000168 ... 0.004263 -0.015080
2020-01-09 0.021241 0.007056 ... 0.010938 0.007656
[5 rows x 8 columns]
相関行列:
Ticker AAPL EWJ ... PG XOM
Ticker ...
AAPL 1.000000 0.569685 ... 0.481491 0.310458
EWJ 0.569685 1.000000 ... 0.446052 0.477005
GLD 0.131189 0.206069 ... 0.123788 0.086030
JNJ 0.427937 0.394592 ... 0.658816 0.314542
JPM 0.456931 0.599323 ... 0.417177 0.593008
MSFT 0.777003 0.586310 ... 0.503727 0.270063
PG 0.481491 0.446052 ... 1.000000 0.246692
XOM 0.310458 0.477005 ... 0.246692 1.000000
[8 rows x 8 columns]
距離行列:
Ticker AAPL EWJ ... PG XOM
Ticker ...
AAPL 0.000000 0.463851 ... 0.509171 0.587172
EWJ 0.463851 0.000000 ... 0.526283 0.511368
GLD 0.659094 0.630052 ... 0.661896 0.676007
JNJ 0.534819 0.550185 ... 0.413028 0.585431
JPM 0.521090 0.447592 ... 0.539825 0.451105
MSFT 0.333914 0.454802 ... 0.498133 0.604126
PG 0.509171 0.526283 ... 0.000000 0.613721
XOM 0.587172 0.511368 ... 0.613721 0.000000
[8 rows x 8 columns]
/Users/yoshihisashinzaki/gemini-cli/blog/script.py:46: ClusterWarning: The symmetric non-negative hollow observation matrix looks suspiciously like an uncondensed distance matrix
linkage_matrix = sch.linkage(dist_matrix, method='ward')
連結行列 (Linkage Matrix):
[[ 0. 5. 0.47277908 2. ]
[ 3. 6. 0.5871942 2. ]
[ 1. 4. 0.64812648 2. ]
[ 7. 10. 0.72717074 3. ]
[ 8. 9. 0.94807667 4. ]
[11. 12. 1.02203895 7. ]
[ 2. 13. 1.20178023 8. ]]これらの可視化は、HRPが単なる数式上のアルゴリズムではなく、金融市場の複雑な関係性をより直感的かつ頑健に捉える手法であることを強く示唆しています。
階層クラスタリング利用における注意点
- 計算コスト:
- 階層クラスタリングは、データ数が多くなると(数万件以上)、計算に時間とメモリを要します。大規模なデータセットに適用する際は注意が必要です。
- デンドログラムの解釈:
- デンドログラムの枝の高さ(距離)や結合順序は重要ですが、枝の左右の交差に意味はありません。その解釈には一定の知識と慣れが求められます。
- 距離尺度の選択:
- どの距離尺度(ユークリッド距離、コサイン類似度など)や連結方法(Ward法、群平均法など)を選択するかで、デンドログラムの形状は大きく変わります。分析の目的に合った手法を選択することが重要です。
- 距離(類似度)の計算方法の詳細は下記ブログを参照してください。
- クラスタ数の決定:
- 階層クラスタリングはクラスタ数を自動で決めませんが、最終的にはデンドログラムをどこでカットしてグループ分けするかを分析者が判断する必要があります。
最後に
階層クラスタリングは、単にデータを分類するだけでなく、その背後にある豊かな構造と関係性を可視化してくれる強力な分析ツールです。K-means法のような高速な手法と目的によって使い分け、データセットの構造を深く探求したい場合には、ぜひこのアプローチの採用を検討してみてください。金融市場の複雑なダイナミクスを解き明かす、新たな洞察が得られるはずです。



コメント