イーサリアムのレイヤー2における必要性と仕組み(前回の復習)
レイヤー1とレイヤー2の概要
ゼロ知識証明(ZK)とKZGコミットメントの概要と理論の説明をする前に前回のブログの復習を行なっておきます。
まず、レイヤー1とは、イーサリアムやビットコインといった基盤となるブロックチェーンを指します。このレイヤーでは、トランザクションの処理、ブロックの生成、セキュリティの提供など、ブロックチェーンの基本的な機能が実行されます。しかし、レイヤー1にはスケーラビリティ、つまりトランザクション処理能力の限界があるため、ネットワークが混雑するとトランザクション手数料(ガス代)が高騰し、処理速度が低下します。
このスケーラビリティの問題を解決するために導入されたのがレイヤー2です。レイヤー2は、レイヤー1の上に構築され、トランザクションをより効率的に処理する補完的な仕組みを提供します。代表的なレイヤー2ソリューションには、Rollups、State Channels、Plasmaなどがあり、特にRollupsは注目を集めています。
レイヤー2におけるゼロ知識証明(ZKP)とKZGコミットメントの役割
ゼロ知識証明(ZKP)とは?
ゼロ知識証明(Zero-Knowledge Proof)とはある情報が正しいことを証明する際に、その情報自体を開示せずに証明を行う暗号技術です。
イーサリアムのレイヤー2ソリューションでは、Rollupsがトランザクションをバッチ処理し、その結果を圧縮してレイヤー1に送信する際にゼロ知識証明が活用されます。これにより、プライバシーを保ちながらもトランザクションの正確性を保証できます。
KZGコミットメントとは?
KZGコミットメントは、レイヤー2において多項式評価の正確性を保証するための暗号技術です。
KZGコミットメントでは、特定の多項式が指定された点で特定の値を持つことを証明し、その多項式自体を公開せずにその正確性を示すことができます。これにより、レイヤー2上でのデータ検証や整合性保証において重要な役割を果たします。特にRollupsでKZGコミットメントを使用することで、大量のデータを効率的に処理し、その正当性をシンプルに証明できます。
なぜレイヤー2が必要なのか?
レイヤー1の制約の問題
イーサリアムのレイヤー1は、高いセキュリティと分散性を持つ一方で、スケーラビリティに制約があります。この制約が原因で、トランザクションの処理遅延や高騰するガス代といった問題が発生します。
これらの問題を解決するためにレイヤー2が登場し、より多くのトランザクションを迅速かつ低コストで処理することが可能になります。
レイヤー2の役割
具体的には、レイヤー2上で多数のトランザクションを一括処理し、その結果だけをレイヤー1に報告することで、全体の処理負荷が軽減されます。この過程でゼロ知識証明やKZGコミットメントが重要な役割を果たし、レイヤー2での処理の正当性と効率性を保ちます。
今回のブログではレイヤー2で機能しているゼロ知識証明(ZK)とKZGコミットメントの役割についての概要と理論について説明しようと思います。
ゼロ知識証明(zkSNARKs)の基本構造とKZGコミットメントの役割
ゼロ知識証明(zkSNARKs)とは?
ゼロ知識証明(ZKP)の一種であるzk-SNARKsは、証明者が秘密情報を一切明かさずに、ある計算が正しいことを証明する技術です。これにより、プライバシーを保ちながら情報の正確性を証明でき、ブロックチェーンやスマートコントラクトで効果的に利用されています。
ゼロ知識証明 (zk-SNARKs) の特長と具体例
入力の秘匿化
zk-SNARKs の大きな特徴は、証明者が持つ情報(例: パスポートのスキャン画像)を明かさずに、特定の主張(例: 20歳以上かどうか)を証明できることです。
検証コストの簡略化
zk-SNARKs を使用することで、証明の検証が迅速かつ効率的に行えるようになります。これにより、ブロックチェーンやスマートコントラクトでの使用が特に有効です。
入力の秘匿化の応用例
パスポートのスキャン画像を用いて、ある人物が20歳以上であるかどうかを判定するという事例を使って応用例を説明します。
function generateAgeProof(photo, name, today) {
const containsName = checkName(photo, name);
if (containsName) {
const age = extractAgeFromPhoto(photo, today);
return age >= 20;
}
return false;
}ステップ1
コードを実行し、「name」と「today」(名前と現在の日付)を入力として与えます。
ステップ2
スキャン画像から名前が含まれているかどうかを確認します(containsName = checkName(photo, name))。
ステップ3
含まれている場合、スキャン画像から年齢を抽出し、20歳以上であれば True を、年齢が20歳未満であれば False を返します。
応用例からわかることのまとめ
この例では、パスポート画像自体を検証者に渡すことなく、名前と年齢の確認を行うことができます。これがゼロ知識証明の「入力の秘匿化」に対応しており、プライバシーを保護しながらも必要な情報の正当性を証明する方法です。
なお、注意点として「実際には写真を偽造される可能性もあるので、この単純な例は教育目的であり、現実的な場面ではさらに複雑な手法が必要」との記述も含まれています。
その他の応用例
その他の具体的な応用例としては、複数のユーザーが行ったトランザクションを一括処理し、その結果をブロックチェーン上で検証することで、トランザクションの整合性と効率を保ちながら、ブロックチェーンの負荷を軽減することなどが考えられます。
まとめ
ゼロ知識証明を使うと、パスワードや送金情報を秘匿しながら、安全な認証やプライバシー保護ができます。また、zkRollupを利用することで、複数のトランザクションをまとめて効率的に処理し、ガスコストを削減できます。
KZGコミットメントとは?
KZGコミットメントは、このzk-SNARKsの中で用いられ、多項式評価の正当性を証明する役割を担っています。KZGコミットメントを利用することで、計算結果の正当性を効率的かつ確実に第三者に示すことが可能です。
KZGコミットメントは、zk-SNARKsの一部として、特定の多項式の正当性を効率的に証明する技術であり、レイヤー2ソリューションで膨大なデータの正当性をコンパクトに示すために使用されています。
ゼロ知識証明(ZKP)とKZGコミットメントの具体例と応用
たとえば、ユーザーがレイヤー2上で複数のトランザクションを行う場合、それらはすべてレイヤー2上で処理され、その結果のみがレイヤー1に送信されます。
このとき、KZGコミットメントが使用され、全トランザクションが正しく処理されたことをコンパクトに証明します。また、ゼロ知識証明が利用され、トランザクションの内容を公開せずにその正当性が検証されます。これにより、ユーザーは迅速かつ安価にトランザクションを行うことができ、イーサリアム全体のセキュリティと信頼性も維持されます。
共通点と相違点
共通点
zk-SNARKsとKZGコミットメントはどちらも、暗号技術を用いて計算結果の正当性を証明することにより、ブロックチェーンやスマートコントラクトの信頼性を確保する役割を果たします。
相違点
zk-SNARKsは主にプライバシー保護と効率的な証明に焦点を当てており、KZGコミットメントは多項式評価の整合性を保証するために使用されます。
ZK(ゼロ知識証明)をコントラクトで使用する際の処理の流れ
Circomを使った処理の流れ

- Trusted Setup:ゼロ知識証明の準備として、秘密の値を生成します。
- Circom言語での記述:Circomという言語で、証明や検証の処理を記述します。
- コンパイル:Circomコードをコンパイルして、実行可能な証明鍵や検証鍵を生成します。
- ブループ生成:記述された処理に基づき、インプットと証明データ(ウィットネス)を使ってゼロ知識証明のブループを生成します。
- アウトプット:生成されたブループが結果として出力され、パブリックインプットとして公開されます。
PlonKを用いた内部処理の流れ


- KZGコミットメントとパブリックパラメータの生成:証明や検証に必要な初期設定として、KZGコミットメントとパブリックパラメータを生成します。
- 制約条件と多項式の設定:証明すべき条件を数式(多項式)として表現し、その制約条件を設定します。
- 証明の生成:設定された制約条件とインプットに基づいて、証明を生成します。
- 検証処理:ベアリング演算を使って、生成された証明が正しいかどうかを検証します。このプロセスはオンチェーンで実行され、結果として正誤が判定されます。
ゼロ知識証明のプロトコルの例
Groth16 (2016)
Groth16は、各回路ごとに事前設定が必要なzkSNARKsの一種で、小さな証明サイズと高速な検証時間を特徴とし、Circom言語でサポートされています。
PlonK (2019)
PlonKは、回路ごとの設定が不要なユニバーサルなzkSNARKsの一種で、Circom言語でサポートされています。

Halo, Halo2 (2019〜)
HaloやHalo2は、他のゼロ知識証明を回路内で検証できるリカーシブなプロトコルで、Rust言語で実装されています。
まとめ
ゼロ知識証明とKZGコミットメントは、イーサリアムのレイヤー2ソリューションにおいて、スケーラビリティとプライバシー保護を向上させるための重要な技術です。これらの技術は、レイヤー1の限界を克服し、より多くのユーザーが快適にブロックチェーンを利用できる環境を提供します。イーサリアムの未来において、これらの技術がどのように活用されるかを理解することで、ブロックチェーン技術の進展に対する洞察を深めることができます。
ゼロ知識証明(ZKP)の算術回路の表現
ゼロ知識証明(ZKP)概要が理解できたと思いますので、更に深いところでの理解を促すためにゼロ知識証明(ZKP)の算術回路の表現について説明します。
算術回路の表現は、計算を形式化して効率的に証明するための手法です。これにより、計算の正確性を秘密情報を明かさずに検証でき、スマートコントラクトやブロックチェーンにおける応用が広がります。また、ゲート制約やコピー制約などの制約条件を導入して、計算の正当性を保証する基盤としても機能します。
PlonKの処理の流れ
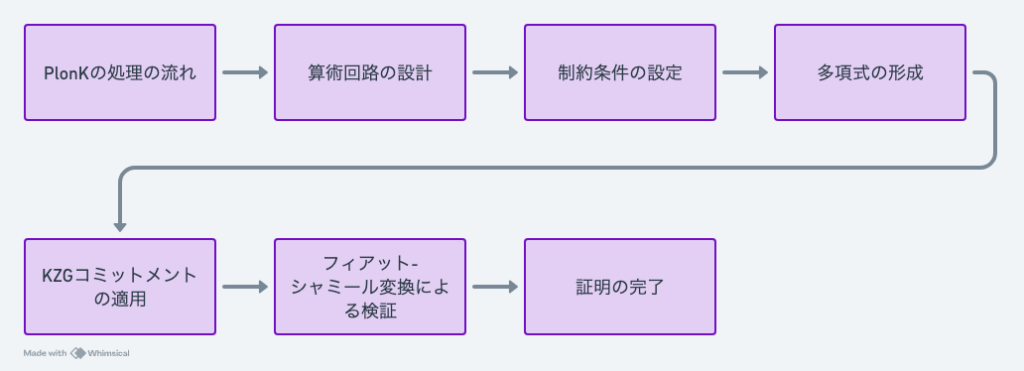
- 算術回路:
ゲートからの入力値を使用して、算術回路が設計されます。これにより、処理が行われる回路が構築されます。 - 制約条件:
多変数から構成される制約が設定されます。この制約条件は、証明を行うための計算に必要なルールを定義します。制約は、具体的な数値や変数に基づいて設定されます。 - 多項式:
設定された制約条件に基づいて、多変数から構成される多項式が形成されます。この多項式は、証明に必要な数式であり、入力値と一致する形に変換されます。 - KZGコミットメント:
多項式に対してKZGコミットメントが適用されます。これは、複数の多項式に対する特定の評価点を計算し、その結果を一意に決定するための重要なステップです。
評価点に対して得られた結果が「フィアット-シャミール」変換を用いて検証されることで、最終的に処理が正しく行われたかどうかを確認します。
算術回路の概要

算術回路は、特定の計算を表現するために用いられる数学的な構造です。
基本的には、加算(+)や乗算(×)などのゲートの組み合わせで表現されます。各ゲートは、入力値に対して計算を行い、出力値を生成します。例えば、「3x + x + 5 = 35」という式を表現する場合、それを構成するゲートや入力値が計算回路上に設定されます。
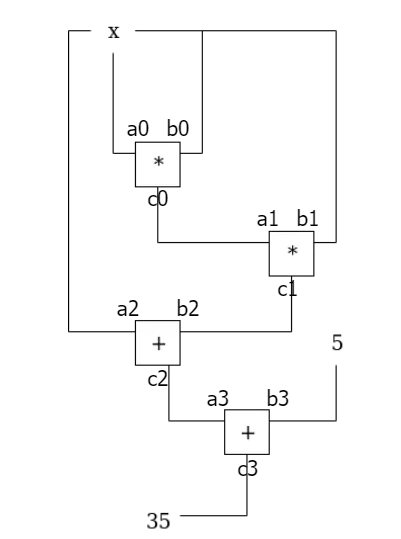
具体的な算術回路の例
リンクの記述では算術回路の例として「3x + x + 5 = 35」を挙げています。この式を達成するために、いくつかのゲート(加算、乗算)と入力値(x、定数)が用いられています。このようにして、入力値が適切に設定されているかどうかを確認することができます。
算術回路の応用
算術回路は、zk-SNARKsなどのゼロ知識証明において重要な役割を果たします。特に、複雑な計算の正当性を証明するために、算術回路を利用して計算が正しく行われていることを示すことができます。この際、計算の入力値や中間結果を秘匿しながら、計算結果のみを公開して正当性を証明することが可能です。
このようにして、算術回路は暗号技術において重要な構成要素となり、ブロックチェーン技術やスマートコントラクトに応用されています。
算術回路から制約条件へ
ゲート制約とコピー制約は、算術回路を具体的な制約に変換するための重要な概念です。これらの制約により、算術回路で表現された計算を証明可能にし、その正当性を保証します。
ゲート制約
ゲート制約とは、算術回路内の各ゲートが、特定の計算を正確に行うために満たすべき条件を示します。たとえば、足し算や掛け算のゲートにおいて、入力値が適切に計算され、期待される出力値が得られるようにするための制約です。これにより、ゲートごとに計算の正確さが保証されます。
具体的には、ゲート制約は次のように設定されます。各ゲートにおける入力(左入力 xL、右入力 xR)と出力 xO の間に以下のような関係が成り立つことが求められます。
加算ゲートの場合:
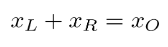
掛け算ゲートの場合:
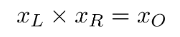
これらの制約を満たすことで、算術回路内での計算が正確に行われていることを証明できます。
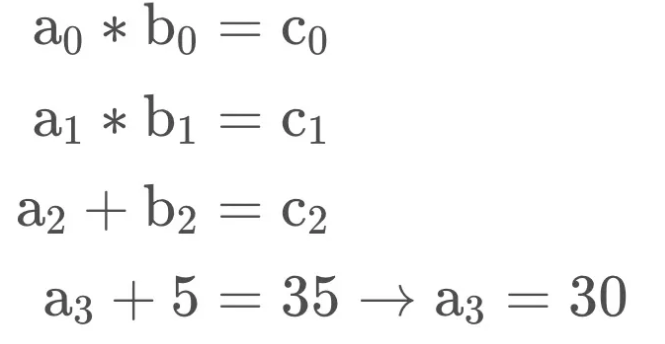
コピー制約
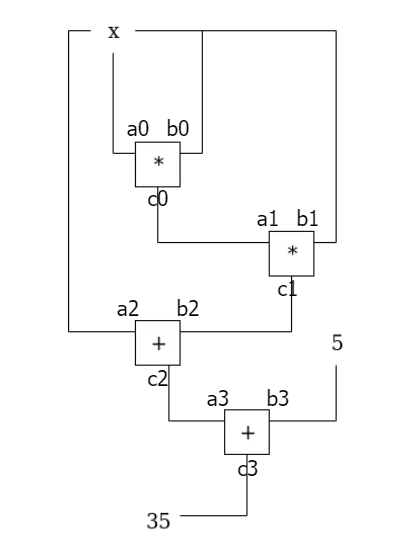
コピー制約は、あるゲートの出力が他のゲートの入力として正しく使用されていることを保証する制約です。これにより、回路内でデータが正確に伝搬されることが確認されます。
たとえば、あるゲートの出力 xO が次のゲートの左入力 xLとして使用される場合、このコピー制約が適用されます。これにより、出力と入力が正確に一致していることが確認できます。
多項式への変換
概要
算術回路をそのまま使うのではなく、これを多項式に変換して扱うことで、証明可能性が向上します。多項式は、特定の点での評価が容易であるため、証明を効率的に行うことができます。
具体例
先ほどの算術回路を多項式に変換すると、次のようになります。
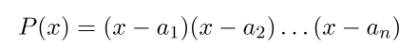
ここで、各 ai はゲートの制約を満たすために選ばれた点です。この多項式を使用することで、ゲート制約やコピー制約を多項式のゼロ点として表現し、証明の一部として利用します。
KZGコミットメント
概要
KZGコミットメントは、多項式の正しさを第三者に証明するための手法です。これにより、証明者は特定の多項式が正しいことを保証しつつ、その内容を公開することなく証明を行うことができます。
計算方法
KZGコミットメントは次の手順で計算されます。
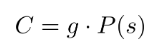
ここで、P(s) は上記の多項式を sという秘密の点で評価したものです。g は事前に選ばれた生成元で、C が生成されます。これにより、特定の多項式に対するコミットメントが生成され、その後の証明に利用されます。
証明の完成
概要
証明者は、コミットメントに基づいて、多項式が特定の点で正しく評価されたことを証明します。これはゼロ知識証明の一部として、公開された情報だけではその多項式の内容を知ることができないという特性を持っています。
具体例
証明者は次のように証明を生成します。
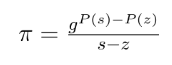
ここで、z は検証者に対して公開されている点であり、π はその点における多項式の評価が正しいことを証明するために使用されます。検証者は、次の式を計算することでその正しさを確認します。
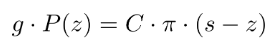
これが成り立つことで、証明が正しいと確認されます。
ゼロ知識証明(ZKP)の算術回路の表現のまとめ
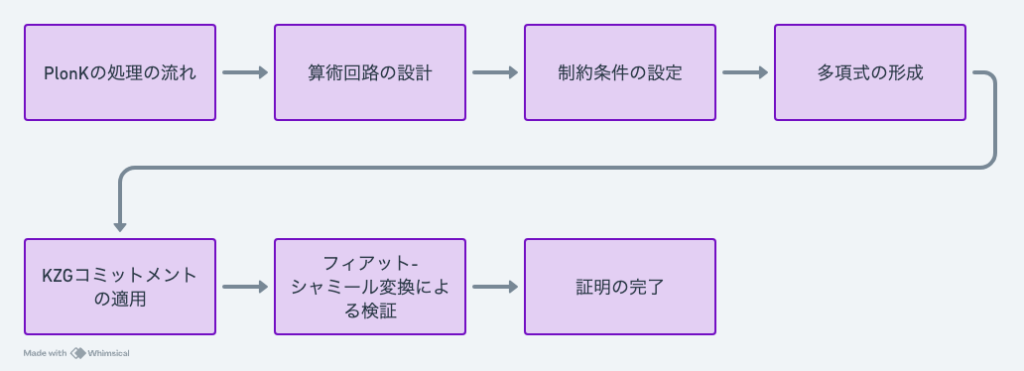
これらのステップの詳細を理解することで、ZKPのプロセス全体がどのように成り立っているか、特にその信頼性と効率性を確保するためにどのような技術が使われているのかを深く理解することができました。
これらの技術は、ブロックチェーンのような分散システムでプライバシーとセキュリティを確保するために非常に重要です。




コメント