前回の振り返り
前回のブログでは、機械学習を支える数学の基礎として確率統計と最適化手法について詳しく学びました。
今回は、情報理論と高度な数学概念が機械学習にどのように貢献するかを探ります。特に、エントロピーやKLダイバージェンスなどの概念を通じて、情報の測定方法とモデルの性能評価を深く理解し、実践的な応用へとつなげることを目指します。
第3回の目標
第3回のブログでは、エントロピーやKLダイバージェンスを通じて情報の測定手法を学び、統計的学習理論や離散数学の重要性を認識します。最前線の技術とその数学的基盤を把握し、実践的な応用へとつなげることを目指します。
- 情報理論の基本概念を理解する
エントロピー、KLダイバージェンス、相互情報量の定義と計算方法を学び、情報の不確実性や分布間の距離を定量化するスキルを習得します。 - 離散数学の応用を探る
グラフ理論や組み合わせ論を用いて、ネットワーク構造や特徴選択の手法を理解し、実際のデータ解析に応用できる能力を養います。 - 数理解析の重要性を認識する
偏微分方程式や変換手法(ラプラス変換、フーリエ変換)の基本を学び、物理シミュレーションや信号処理における応用を理解します。 - 統計的学習理論を学ぶ
汎化誤差、VC次元、PAC学習の概念を理解し、機械学習モデルの性能評価や改善方法を学びます。 - 特殊分野の理解を深める
微分幾何学や確率過程(マルコフ連鎖、ガウス過程)の基礎を学び、機械学習の理論的側面や時系列データ解析における役割を理解します。
これらの学習目標を通じて、情報理論と高度な数学が機械学習の進化を支える重要な基盤であることを実感し、今後の学習に活かしていきましょう。
情報理論
情報理論は、情報の量や伝達方法を数学的に扱う分野であり、機械学習においても重要な役割を果たします。ここでは、エントロピー、KLダイバージェンス、相互情報量、クロスエントロピーについて説明します。
エントロピー
情報の不確実性の測定方法
エントロピーは、情報の不確実性やランダム性を定量化する指標です。情報理論におけるエントロピー $H_(X)$ は、離散確率変数 $X$ の各状態 $x_i$ が発生する確率 $p(x_i)$ を用いて次のように定義されます。
$$H(X) = -\sum_{i} p(x_i) \log p(x_i)$$
具体例:例えば、コインを投げたときに表が出る確率 $p$ が $0.5$ の場合、エントロピーは以下のように計算されます。
$$H(X) = -[0.5 \log 0.5 + 0.5 \log 0.5]$$
底の指定:上記の数式では、対数の底が明示されていませんが、通常は底2の対数($\log_2$)を用います。したがって、$\log 0.5$ は $\log_2 0.5$ と解釈します。
$$\log_2 0.5 = \log_2 \left( \frac{1}{2} \right) = \log_2(2^{-1}) = -1$$
故に
$$H(X) = -[0.5 \log_2 0.5 + 0.5 \log_2 0.5]= -[0.5 \times (-1) + 0.5 \times (-1)] = 1$$
※ エントロピーが高いほど、不確実性が高いことを意味します。完全に予測可能な場合(例えば、常に表が出る場合)、エントロピーは 0 になります。
利用例)
エントロピーは、データの不確実性やランダム性を測定するために使用されます。特に、特徴選択や決定木アルゴリズム(例:ID3、C4.5)において、情報利得を計算する際に用いられます。
import numpy as np
import matplotlib.pyplot as plt # 追加
import japanize_matplotlib
def entropy(probabilities):
"""
エントロピーを計算する関数
probabilities: 確率のリスト
"""
return -np.sum(probabilities * np.log2(probabilities + 1e-9)) # 0除算防止
# 例:コインの表が出る確率が0.5の場合
probabilities = [0.5, 0.5]
H = entropy(np.array(probabilities))
print(f"エントロピー H(X): {H}")
# 可視化のためのコードを追加
labels = ['表', '裏'] # ラベル
plt.bar(labels, probabilities) # 棒グラフを描画
plt.title(f"エントロピー H(X): {H:.2f}") # タイトルにエントロピーを表示
plt.ylabel("確率") # Y軸のラベル
plt.show() # グラフを表示エントロピー H(X): 0.99999999711461
KLダイバージェンス(カルバック・ライブラーダイバージェンス)
分布間の距離の測定
KLダイバージェンス $D_{KL}(P || Q)$ は、確率分布 $P$ と $Q$ の間の「距離」を測る指標です。特に $Q$ に基づく $P$ の情報損失を示します。
$$D_{KL}(P \| Q) = \sum_{i} p(x_i) [\log \frac{p(x_i)}{q(x_i)}] = \sum_{i} p(x_i) [\log{p(x_i)} – {q(x_i)}]$$
$P$と$Q$が同じ分布の場合に限り、KLダイバージェンスは最小値0となる。※$DKL$は非負。2つの分布に差があるほど、値は大きくなる
モデルの近似度評価への応用
機械学習では、真の分布 $P$ とモデルが仮定する分布 $Q$ の間の距離を測るためにKLダイバージェンスが用いられます。KLダイバージェンスが小さいほど、モデルの分布 $Q$ が真の分布 $P$ に近いことを示します。
利用例)
KLダイバージェンスは、2つの確率分布間の「距離」を測定するために使用されます。主に、生成モデル(例:変分オートエンコーダー)や分布の近似において、モデル分布と真の分布の差異を評価する際に利用されます。
import numpy as np
def kl_divergence(p, q):
"""
KLダイバージェンスを計算する関数
p, q: 確率分布のリスト(同じ長さ)
"""
p = np.array(p)
q = np.array(q)
return np.sum(p * np.log(p / (q + 1e-9) + 1e-9)) # 0除算防止
# 例:PとQの分布
P = [0.4, 0.6]
Q = [0.5, 0.5]
D_KL = kl_divergence(P, Q)
print(f"KLダイバージェンス D_KL(P||Q): {D_KL}")KLダイバージェンス D_KL(P||Q): 0.020135512550688947| ダイバージェンス | 利用場面 |
|---|---|
| KLダイバージェンス | 生成モデル(例: Variational Autoencoders)におけるパラメータ調整 強化学習でのポリシー比較 情報理論に基づくモデル評価 |
KLダイバージェンスを使って強化学習でのポリシー比較を行ってみる
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
def kl_divergence(p, q):
"""
KLダイバージェンスを計算する関数
p, q: 確率分布のリスト(同じ長さ)
"""
p = np.array(p)
q = np.array(q)
return np.sum(p * np.log(p / (q + 1e-9) + 1e-9)) # 0除算防止
# ポリシーAとポリシーBの確率分布を定義
policy_A = [0.7, 0.2, 0.1] # 行動1, 行動2, 行動3の確率
policy_B = [0.6, 0.3, 0.1] # 行動1, 行動2, 行動3の確率
# KLダイバージェンスを計算
D_KL = kl_divergence(policy_A, policy_B)
print(f"KLダイバージェンス D_KL(Policy A || Policy B): {D_KL}")
# ポリシーBからポリシーAへのKLダイバージェンスも計算
D_KL_reverse = kl_divergence(policy_B, policy_A)
print(f"KLダイバージェンス D_KL(Policy B || Policy A): {D_KL_reverse}")
# 可視化
labels = ['行動1', '行動2', '行動3']
x = np.arange(len(labels)) # ラベルの位置
# 棒グラフを描画
width = 0.35 # 棒の幅
fig, ax = plt.subplots()
bars1 = ax.bar(x - width/2, policy_A, width, label='ポリシーA', color='blue')
bars2 = ax.bar(x + width/2, policy_B, width, label='ポリシーB', color='orange')
# グラフの装飾
ax.set_ylabel('確率')
ax.set_title('ポリシーの比較')
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend()
# KLダイバージェンスの値を表示
ax.text(0, 0.05, f'D_KL(A||B): {D_KL:.4f}', color='black', ha='center')
ax.text(1, 0.05, f'D_KL(B||A): {D_KL_reverse:.4f}', color='black', ha='center')
plt.ylim(0, 1) # Y軸の範囲
plt.show()KLダイバージェンス D_KL(Policy A || Policy B): 0.02681245242411472
KLダイバージェンス D_KL(Policy B || Policy A): 0.02914912217895144
JSダイバージェンス(ジェンセン・シャノンダイバージェンス)
KLダイバージェンスは対称性がないため、$D_{KL}(P | Q)$ と $D_{KL}(Q | P)$ のどちらを使うかによって結果が変わります。KLダイバージェンスを基にした対称な距離で、2つの確率分布 $P$ と $Q$ の平均分布 $M$ を使って計算されます。
$$D_{JS}(P \| Q) = \frac{1}{2} D_{KL}(P \| M) + \frac{1}{2} D_{KL}(Q \| M)$$
- $M=\frac{1}{2}(P + Q)$
$M$を代入すると
$$D_{JS}(P \| Q) = \frac{1}{2} \left\{ D_{KL} \left( P \| \frac{P + Q}{2} \right) + D_{KL} \left( Q \| \frac{P + Q}{2} \right) \right\}$$
要約すると、KLダイバージェンスは非対称で特定の分布の情報損失を評価するのに対し、JSダイバージェンスは対称で2つの分布の類似性を測定するために使われます。
使用例)
確率分布の間の類似性を評価するため、特にクラスタリングや情報検索、生成モデルの評価に使用されます。
import numpy as np
def kl_divergence(p, q):
"""KLダイバージェンスを計算する関数"""
return np.sum(np.where(p != 0, p * np.log(p / q), 0))
def js_divergence(p, q):
"""Jensen-Shannonダイバージェンスを計算する関数"""
# 確率分布を正規化
p = np.array(p) / np.sum(p)
q = np.array(q) / np.sum(q)
# 平均分布Mを計算
m = 0.5 * (p + q)
# KLダイバージェンスを計算
return 0.5 * kl_divergence(p, m) + 0.5 * kl_divergence(q, m)
# 確率分布PとQを定義
P = [0.1, 0.9]
Q = [0.9, 0.1]
# JSダイバージェンスを計算
js_result = js_divergence(P, Q)
print(f"Jensen-Shannon Divergence: {js_result}")Jensen-Shannon Divergence: 0.3680642071684971| ダイバージェンス | 利用場面 |
|---|---|
| JSダイバージェンス | データ分布の比較 異なるモデル出力の類似性評価 クラスタリングや分類問題における分布の類似性確認 |
JSダイバージェンスをクラスタリングで使ってみる
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
def kl_divergence(p, q):
"""KLダイバージェンスを計算する関数"""
return np.sum(np.where(p != 0, p * np.log(p / q), 0))
def js_divergence(p, q):
"""Jensen-Shannonダイバージェンスを計算する関数"""
p = np.array(p) / np.sum(p)
q = np.array(q) / np.sum(q)
m = 0.5 * (p + q)
return 0.5 * kl_divergence(p, m) + 0.5 * kl_divergence(q, m)
# データを生成
X, y = make_blobs(n_samples=300, centers=2, cluster_std=0.60, random_state=0)
# KMeansクラスタリングを実行
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
labels = kmeans.labels_
# 各クラスタの確率分布を計算
cluster_0 = X[labels == 0]
cluster_1 = X[labels == 1]
# 確率分布をヒストグラムとして計算
hist_0, _ = np.histogram(cluster_0, bins=10, density=True)
hist_1, _ = np.histogram(cluster_1, bins=10, density=True)
# JSダイバージェンスを計算
js_result = js_divergence(hist_0, hist_1)
# 結果を表示
print(f"Jensen-Shannon Divergence between clusters: {js_result}")
# クラスタをプロット
plt.scatter(X[:, 0], X[:, 1], c=labels, s=30, cmap='viridis')
plt.title("KMeans Clustering")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()Jensen-Shannon Divergence between clusters: 0.17487399159087064
相互情報量
特徴量間の関連性の測定
相互情報量 $I{(X; Y)}$ は、2つの確率変数 $X$ と $Y$ 間の依存関係を測定する指標です。定義は以下の通りです。
特徴:線形・非線形の関係を問わず、2つの変数間の依存関係を捉えることができます。
$$I(X; Y) = \sum_{x,y} p(x, y) \log \frac{p(x, y)}{p(x) p(y)}$$
相互情報量が高いほど、 $X$ と $Y$ 間の依存関係が強いことを示します。特徴選択などで、相互情報量を用いて関連性の高い特徴量を選ぶことができます。相関係数の式と類似していますが、相関係数は線形関係に特化しており、非線形の依存関係を捉えることはできません。
使用例)
相互情報量は、2つの特徴量間の依存関係を測定するために使用されます。特徴選択や特徴エンジニアリングにおいて、相関関係のない特徴を選ぶ際に利用されます。
線形の場合
import numpy as np
from sklearn.metrics import mutual_info_score
def mutual_information(x, y):
"""
相互情報量を計算する関数
x, y: 同じ長さのリストまたは配列
"""
return mutual_info_score(x, y)
# 例:2つの特徴量
X = [0, 0, 1, 1, 2, 2]
Y = [0, 1, 0, 1, 0, 1]
I_XY = mutual_information(X, Y)
print(f"相互情報量 I(X; Y): {I_XY}")相互情報量 I(X; Y): 0.0上記の例では、XとYは独立しているため相互情報量は0となります。実際のデータでは、相互情報量が高いほど依存関係が強いことを示します。
非線形の場合
import numpy as np
from sklearn.metrics import mutual_info_score
import matplotlib.pyplot as plt
def mutual_information(x, y):
"""
相互情報量を計算する関数
x, y: 同じ長さのリストまたは配列
"""
return mutual_info_score(x, y)
# 非線形なデータを生成
np.random.seed(0)
X = np.random.rand(100) # 0から1の間のランダムな値
Y = np.sin(2 * np.pi * X) + np.random.normal(0, 0.1, 100) # 非線形関係にノイズを加える
# 相互情報量を計算
I_XY = mutual_information(np.round(X, 2), np.round(Y, 2)) # 小数点以下2桁で丸める
print(f"相互情報量 I(X; Y): {I_XY}")
# データを可視化
plt.scatter(X, Y, alpha=0.5)
plt.title("非線形データの散布図")
plt.xlabel("X")
plt.ylabel("Y")
plt.grid()
plt.show()相互情報量 I(X; Y): 3.8147113794821865
クロスエントロピー
分類問題における損失関数の役割
クロスエントロピーは$H(p, q)$、機械学習の分類問題において、モデルの予測$q$と実際のラベル$p$との誤差を定量化する損失関数です。
具体的には、モデルが各クラスに対して予測した確率と、実際のクラスの確率分布との間の差異を測定します。この損失関数は、モデルが正しいクラスに高い確率を割り当てるように学習を促進し、最適化アルゴリズムを通じてモデルのパラメータを調整します。
クロスエントロピーは、モデルの予測が実際の分布にどれだけ近いかを示す指標として広く使用されています。
$$H(p, q) = -\sum_{i} p(x_i) \log q(x_i)$$
機械学習の分類問題では、クロスエントロピーが損失関数としてよく使用されます。モデルの予測分布 $q$ が真の分布 $p$ に近づくように、損失関数を最小化します。
使用例)
クロスエントロピーは、分類問題における損失関数として使用されます。特に、ニューラルネットワークの出力層でソフトマックス関数と組み合わせて用いられ、モデルの予測と実際のラベルとの不一致を測定します。
import numpy as np
def cross_entropy(p, q):
"""
クロスエントロピーを計算する関数
p: 真の分布(ワンホットベクトル)
q: 予測分布(確率ベクトル)
"""
p = np.array(p)
q = np.array(q)
return -np.sum(p * np.log(q + 1e-9)) # 0除算防止
# 例:2クラス分類
# 真のラベル(クラス0)
p_true = [1, 0]
# モデルの予測確率
q_pred = [0.7, 0.3]
CE = cross_entropy(p_true, q_pred)
print(f"クロスエントロピー H(p, q): {CE}")クロスエントロピー H(p, q): 0.3566749425101611import matplotlib.pyplot as plt
# 可視化のための関数を追加します
def plot_distributions(p, q):
"""
真の分布と予測分布を可視化する関数
p: 真の分布(ワンホットベクトル)
q: 予測分布(確率ベクトル)
"""
labels = ['クラス0', 'クラス1']
x = np.arange(len(labels))
# 棒グラフを作成
width = 0.35
fig, ax = plt.subplots()
bars1 = ax.bar(x - width/2, p, width, label='真の分布 (p)')
bars2 = ax.bar(x + width/2, q, width, label='予測分布 (q)')
# グラフの装飾
ax.set_ylabel('確率')
ax.set_title('真の分布と予測分布の比較')
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend()
# 値を表示
for bar in bars1 + bars2:
height = bar.get_height()
ax.annotate(f'{height:.2f}',
xy=(bar.get_x() + bar.get_width() / 2, height),
xytext=(0, 3), # 3ポイント上にテキストを表示
textcoords="offset points",
ha='center', va='bottom')
plt.show()
# 可視化を実行
plot_distributions(p_true, q_pred)
クロスエントロピーをソフトマックス関数の出力に適用
# ソフトマックス関数を計算する関数を追加します
def softmax(logits):
"""
ソフトマックス関数を計算する関数
logits: ロジット(未正規化の確率)
"""
exp_logits = np.exp(logits - np.max(logits)) # オーバーフロー防止
return exp_logits / np.sum(exp_logits)
# 例:ロジットからソフトマックスを計算
logits = [2.0, 1.0, 0.1]
q_softmax = softmax(logits)
print(f"ソフトマックス確率: {q_softmax}")
p_true = [1, 0, 0] # クラス0が真のラベル
# クロスエントロピーをソフトマックスの出力に適用
CE_softmax = cross_entropy(p_true, q_softmax)
print(f"ソフトマックスを用いたクロスエントロピー H(p, q): {CE_softmax}")ソフトマックス確率: [0.65900114 0.24243297 0.09856589]
ソフトマックスを用いたクロスエントロピー H(p, q): 0.4170300147603855ソフトマックス関数の確率の総和は1になります。
# ソフトマックスの出力とクロスエントロピーを可視化する関数を追加します
def plot_softmax_and_cross_entropy(p, q, ce):
"""
ソフトマックスの出力とクロスエントロピーを可視化する関数
p: 真の分布(ワンホットベクトル)
q: ソフトマックスの出力(確率ベクトル)
ce: クロスエントロピーの値
"""
labels = ['クラス0', 'クラス1', 'クラス2']
x = np.arange(len(labels))
# 棒グラフを作成
width = 0.35
fig, ax = plt.subplots()
bars1 = ax.bar(x - width/2, p, width, label='真の分布 (p)')
bars2 = ax.bar(x + width/2, q, width, label='ソフトマックス出力 (q)')
# グラフの装飾
ax.set_ylabel('確率')
ax.set_title(f'真の分布とソフトマックス出力の比較 (クロスエントロピー: {ce:.4f})')
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend()
# 値を表示
for bar in bars1 + bars2:
height = bar.get_height()
ax.annotate(f'{height:.2f}',
xy=(bar.get_x() + bar.get_width() / 2, height),
xytext=(0, 3), # 3ポイント上にテキストを表示
textcoords="offset points",
ha='center', va='bottom')
plt.show()
# 可視化を実行
plot_softmax_and_cross_entropy(p_true, q_softmax, CE_softmax)
クロスエントロピーの値が小さいほど、モデルの予測が真の分布に近いことを示しますが、0.4170はあくまでその時点での誤差の指標であり、最小誤差ではありません。モデルの性能を向上させるためには、さらなる学習や調整が必要です。
二値クロスエントロピー
二値クロスエントロピーは、機械学習の二値分類問題において、モデルの予測と実際のラベルとの誤差を定量化する損失関数です。
二項分布に基づく交差エントロピーを表しており、確率 $p$ に対する推定確率 $q$ の精度を評価するために用いられます。
$$H(p, q) = -[p \log q + (1 – p) \log(1 – q)]$$
$p$は真のラベル(0または1)、$q$はモデルの予測確率(1である確率)です。値が小さいほど、モデルの予測が真のラベルに近いことを示します。
使用例)
スパムメールの判定(スパムか非スパムか)や、病気の有無の判定(陽性か陰性か)など、2つのクラスに分類する問題に使用されます。
import numpy as np
def binary_cross_entropy(y_true, y_pred):
"""
二値クロスエントロピーを計算する関数
y_true: 真のラベル(0または1)
y_pred: 予測確率(0から1の範囲)
"""
y_true = np.array(y_true)
y_pred = np.array(y_pred)
return -np.mean(y_true * np.log(y_pred + 1e-9) + (1 - y_true) * np.log(1 - y_pred + 1e-9)) # 0除算防止
# 例:二値分類
# 真のラベル(クラス1)
y_true = [1]
# モデルの予測確率
y_pred = [0.8]
BCE = binary_cross_entropy(y_true, y_pred)
print(f"二値クロスエントロピー H(y_true, y_pred): {BCE}")二値クロスエントロピー H(y_true, y_pred): 0.22314355006420974import matplotlib.pyplot as plt
def plot_binary_cross_entropy(y_true, y_pred, bce):
"""
二値クロスエントロピーを可視化する関数
y_true: 真のラベル(0または1)
y_pred: 予測確率(0から1の範囲)
bce: 二値クロスエントロピーの値
"""
labels = ['クラス0', 'クラス1']
x = np.arange(len(labels))
# 棒グラフを作成
width = 0.35
fig, ax = plt.subplots()
bars1 = ax.bar(x - width/2, [1 - y_true[0], y_true[0]], width, label='真のラベル (y_true)')
bars2 = ax.bar(x + width/2, [1 - y_pred[0], y_pred[0]], width, label='予測確率 (y_pred)')
# グラフの装飾
ax.set_ylabel('確率')
ax.set_title(f'二値クロスエントロピーの可視化 (BCE: {bce:.4f})')
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend()
# 値を表示
for bar in bars1 + bars2:
height = bar.get_height()
ax.annotate(f'{height:.2f}',
xy=(bar.get_x() + bar.get_width() / 2, height),
xytext=(0, 3), # 3ポイント上にテキストを表示
textcoords="offset points",
ha='center', va='bottom')
plt.show()
# 可視化を実行
plot_binary_cross_entropy(y_true, y_pred, BCE)
二値クロスエントロピーをシグモイド関数の出力に適用
import numpy as np
def sigmoid(logits):
"""
シグモイド関数を計算する関数
logits: ロジット(未正規化の確率)
"""
return 1 / (1 + np.exp(-logits))
def binary_cross_entropy(y_true, y_pred):
"""
二値クロスエントロピーを計算する関数
y_true: 真のラベル(0または1)
y_pred: 予測確率(0から1の範囲)
"""
y_true = np.array(y_true)
y_pred = np.array(y_pred)
return -np.mean(y_true * np.log(y_pred + 1e-9) + (1 - y_true) * np.log(1 - y_pred + 1e-9)) # 0除算防止
# 例:ロジットからシグモイドを計算
logits = 0.5 # 任意のロジット値
y_pred = sigmoid(logits)
print(f"シグモイド出力: {y_pred}")
# 真のラベル(クラス1)
y_true = [1]
# 二値クロスエントロピーを計算
BCE = binary_cross_entropy(y_true, [y_pred])
print(f"二値クロスエントロピー H(y_true, y_pred): {BCE}")シグモイド出力: 0.6224593312018546
二値クロスエントロピー H(y_true, y_pred): 0.474076982573576import matplotlib.pyplot as plt
def plot_sigmoid_and_binary_cross_entropy(y_true, y_pred, bce):
"""
シグモイドの出力と二値クロスエントロピーを可視化する関数
y_true: 真のラベル(0または1)
y_pred: シグモイドの出力(確率)
bce: 二値クロスエントロピーの値
"""
labels = ['クラス0', 'クラス1']
x = np.arange(len(labels))
# 棒グラフを作成
width = 0.35
fig, ax = plt.subplots()
bars1 = ax.bar(x - width/2, [1 - y_true[0], y_true[0]], width, label='真のラベル (y_true)')
bars2 = ax.bar(x + width/2, [1 - y_pred[0], y_pred[0]], width, label='シグモイド出力 (y_pred)')
# グラフの装飾
ax.set_ylabel('確率')
ax.set_title(f'シグモイド出力と二値クロスエントロピーの可視化 (BCE: {bce:.4f})')
ax.set_xticks(x)
ax.set_xticklabels(labels)
ax.legend()
# 値を表示
for bar in bars1 + bars2:
height = bar.get_height()
ax.annotate(f'{height:.2f}',
xy=(bar.get_x() + bar.get_width() / 2, height),
xytext=(0, 3), # 3ポイント上にテキストを表示
textcoords="offset points",
ha='center', va='bottom')
plt.show()
# 可視化を実行
plot_sigmoid_and_binary_cross_entropy(y_true, [y_pred], BCE)
シグモイド関数は、出力を0から1の範囲に制限します。これにより、出力は確率として解釈でき、シグモイド関数の出力は、特定のクラスに属する確率を示しています。
離散数学
離散数学は、有限または可算無限の離散的な構造を扱う数学の分野です。機械学習では、データ構造やアルゴリズムの基礎として重要です。ここでは、グラフ理論、組み合わせ論、論理演算について説明します。
グラフ理論
グラフ理論は、点(頂点)とそれらを結ぶ線(辺)から構成されるグラフを研究する分野です。グラフは、ネットワークの構造や関係性を表すのに非常に便利です。
ネットワーク構造の解析方法
グラフ理論は、頂点(ノード)とそれらを結ぶ辺(エッジ)からなるグラフを用いて、ネットワーク構造を解析します。グラフは次のように表されます。
$$G=(V,E)$$
ここで、 $V$ は頂点の集合、 $E$ は辺の集合です。グラフ理論を用いることで、ソーシャルネットワークや通信ネットワークの構造を理解し、分析することができます。
グラフニューラルネットワークの基礎
グラフニューラルネットワーク(GNN)は、グラフ構造を持つデータを扱うためのニューラルネットワークです。GNNは、各ノードの特徴量を隣接するノードからの情報を集約することで更新します。このプロセスを繰り返すことで、グラフ全体の情報を効果的に学習します。
使用例)
グラフ理論は、ネットワーク構造の解析や最適化問題、ソーシャルネットワーク分析などに利用されます。特に、グラフニューラルネットワーク(GNN)では、グラフ構造を持つデータを効果的に学習するために使用されます。
ネットワークの作成と可視化
import networkx as nx
import matplotlib.pyplot as plt
# グラフの作成
G = nx.Graph()
# ノードの追加
G.add_nodes_from([1, 2, 3, 4, 5])
# エッジの追加
G.add_edges_from([(1, 2), (1, 3), (2, 4), (3, 5)])
# グラフの描画
nx.draw(G, with_labels=True, node_color='lightblue', edge_color='gray', node_size=500)
plt.title("ネットワーク構造の例")
plt.show()
グラフニューラルネットワークの基礎
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
# グラフニューラルネットワークの基礎実装
class GNNLayer(nn.Module):
def __init__(self, input_dim, output_dim):
super(GNNLayer, self).__init__()
self.linear = nn.Linear(input_dim, output_dim)
def forward(self, x, adj):
# 隣接行列を用いてメッセージを集約
x = torch.matmul(adj, x)
return self.linear(x)
class GNN(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(GNN, self).__init__()
self.layer1 = GNNLayer(input_dim, hidden_dim)
self.layer2 = GNNLayer(hidden_dim, output_dim)
def forward(self, x, adj):
x = self.layer1(x, adj)
x = torch.relu(x)
x = self.layer2(x, adj)
return x
# ノードの特徴量を定義(例としてランダムな値を使用)
num_nodes = G.number_of_nodes()
input_dim = 3 # 特徴量の次元
x = torch.rand(num_nodes, input_dim)
# 隣接行列を作成
adj = nx.to_numpy_array(G)
# GNNのインスタンスを作成
gnn = GNN(input_dim, hidden_dim=4, output_dim=2)
# フォワードパスを実行
output = gnn(x, torch.FloatTensor(adj))
print("GNNの出力:", output)GNNの出力: tensor([[ 0.4869, 0.2239],
[ 0.6349, 0.2873],
[ 0.4940, 0.3406],
[ 0.2781, -0.0594],
[ 0.4137, -0.0508]], grad_fn=<AddmmBackward0>)この出力は、グラフニューラルネットワーク(GNN)のフォワードパスの結果として得られたノードの特徴量を表しています。具体的には、以下のような情報を含んでいます。
- テンソルの形状:ノード数, 出力次元
- ノードの出力特徴:上からノードの新しい特徴量を示す
- 学習可能なパラメータ:grad_fn=(テンソルがどのように計算されたかを示す情報)
- ノードの埋め込み:出力は、各ノードの埋め込み(特徴量の表現)を示しており、これを用いてノードの分類や回帰、クラスタリングなどのタスクに利用することができる。
要するに、この出力はGNNが各ノードに対して計算した新しい特徴量のセットであり、これを使ってさらに処理を行うことができます。
組み合わせ論
特徴選択やデータの分割手法
組み合わせ論は、有限集合の部分集合や順列、組み合わせの数を扱います。機械学習では、特徴選択やデータの分割手法に応用されます。例えば、特徴選択では、全ての特徴の組み合わせを考慮して最適な特徴セットを選びます。
組み合わせの公式:組み合わせは選択の順序を無視し、特定のアイテムのグループを選ぶ際に使います。
$$C(n, r) = \frac{n!}{r!(n – r)!}$$
組み合わせは、n個のアイテムからr個を選ぶ方法の数を示します。この際、選ぶ順序は考慮されません。たとえば、5種類の果物から3つを選ぶ場合、りんご、バナナ、オレンジを選んだとき、バナナ、オレンジ、りんごを選んだ場合と同じとみなされます。
順列の公式:順列は選択の順序を重視し、特定のアイテムの並びを考える場合に用います。
$$P(n, r) = \frac{n!}{(n – r)!}$$
順列は、n個のアイテムからr個を選び、選んだアイテムの順序を考慮して並べる方法の数を示します。たとえば、5種類の果物から3つを選ぶ場合、りんご、バナナ、オレンジの組み合わせと、バナナ、オレンジ、りんごの組み合わせは異なる順列としてカウントされます。
第2回のブログに組み合わせについての詳しい内容を記載していますので確認してみて下さい。
使用例)
組み合わせ論は、特徴選択やハイパーパラメータのチューニングなど、最適な組み合わせを探索する際に使用されます。特に、全ての組み合わせを試す場合や、特定の条件を満たす組み合わせを選ぶ際に利用されます。
組み合わせの生成
import itertools
def generate_combinations(n, r):
"""
n個からk個を選ぶ組み合わせを生成する関数
"""
return list(itertools.combinations(range(1, n+1), r))
# 例:5個から3個を選ぶ組み合わせ
combinations = generate_combinations(5, 3)
print("組み合わせの数:", len(combinations))
print("組み合わせ:", combinations)組み合わせの数: 10
組み合わせ: [(1, 2, 3), (1, 2, 4), (1, 2, 5), (1, 3, 4), (1, 3, 5), (1, 4, 5), (2, 3, 4), (2, 3, 5), (2, 4, 5), (3, 4, 5)]順列の生成
import itertools
def generate_permutations(n, r):
"""
n個からk個を選ぶ順列を生成する関数
"""
return list(itertools.permutations(range(1, n+1), r))
# 例:5個から3個を選ぶ順列
permutations = generate_permutations(5, 3)
print("順列の数:", len(permutations))
print("順列:", permutations)順列の数: 60
順列: [(1, 2, 3), (1, 2, 4), (1, 2, 5), (1, 3, 2), (1, 3, 4), (1, 3, 5), (1, 4, 2), (1, 4, 3), (1, 4, 5), (1, 5, 2), (1, 5, 3), (1, 5, 4), (2, 1, 3), (2, 1, 4), (2, 1, 5), (2, 3, 1), (2, 3, 4), (2, 3, 5), (2, 4, 1), (2, 4, 3), (2, 4, 5), (2, 5, 1), (2, 5, 3), (2, 5, 4), (3, 1, 2), (3, 1, 4), (3, 1, 5), (3, 2, 1), (3, 2, 4), (3, 2, 5), (3, 4, 1), (3, 4, 2), (3, 4, 5), (3, 5, 1), (3, 5, 2), (3, 5, 4), (4, 1, 2), (4, 1, 3), (4, 1, 5), (4, 2, 1), (4, 2, 3), (4, 2, 5), (4, 3, 1), (4, 3, 2), (4, 3, 5), (4, 5, 1), (4, 5, 2), (4, 5, 3), (5, 1, 2), (5, 1, 3), (5, 1, 4), (5, 2, 1), (5, 2, 3), (5, 2, 4), (5, 3, 1), (5, 3, 2), (5, 3, 4), (5, 4, 1), (5, 4, 2), (5, 4, 3)]論理演算
条件判断や回帰木での応用
論理演算は、真偽値を扱う演算であり、機械学習の条件判断や決定木、回帰木の分岐条件として利用されます。基本的な論理演算には、AND、OR、NOT などがあります。
以下に、論理演算のAND、ORおよびNOTの定義を示します。
AND(論理積)
両方の入力が1のときにのみ1を返す演算です。
$$\text{AND: } A \land B =
\begin{cases}
1 & \text{if } A = 1 \text{ and } B = 1 \\
0 & \text{otherwise}
\end{cases}$$
OR(論理和)
OR演算は、いずれかの入力が1であれば1を返す。
$$\text{OR: } A \lor B =
\begin{cases}
1 & \text{if } A = 1 \text{ or } B = 1 \\
0 & \text{if } A = 0 \text{ and } B = 0
\end{cases}$$
NOT(論理否定)
NOT演算は入力が0であれば1を返し、入力が1であれば0を返します。
$$\text{NOT: } \neg A =
\begin{cases}
1 & \text{if } A = 0 \\
0 & \text{if } A = 1
\end{cases}$$
使用例)
論理演算は、条件判断や決定木、回帰木の分岐条件として利用されます。特に、データの特徴に基づいて条件を設定し、分類や回帰を行う際に使用されます。
def logical_and(a, b):
return a and b
def logical_or(a, b):
return a or b
def logical_not(a):
return not a
# 例:論理演算の使用
A = True
B = False
print(f"A AND B: {logical_and(A, B)}")
print(f"A OR B: {logical_or(A, B)}")
print(f"NOT A: {logical_not(A)}")A AND B: False
A OR B: True
NOT A: False決定木の分岐条件
目的は、カテゴリカルなクラスラベルを予測することです。今回は顧客の購買行動を予測し分類する例です。
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
import matplotlib.pyplot as plt
from sklearn import tree
# サンプルデータの作成
data = {
'年齢': [22, 25, 47, 35, 46, 56, 23, 34, 45, 36],
'収入': [15000, 18000, 30000, 25000, 32000, 40000, 16000, 24000, 35000, 29000],
'購買': ['いいえ', 'はい', 'はい', 'いいえ', 'はい', 'はい', 'いいえ', 'いいえ', 'はい', 'はい']
}
# DataFrameの作成
df = pd.DataFrame(data)
# 特徴量とラベルの分割
X = df[['年齢', '収入']]
y = df['購買']
# データの分割(訓練データとテストデータ)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 決定木モデルの作成
model = DecisionTreeClassifier()
# モデルの学習
model.fit(X_train, y_train)
# テストデータでの予測
y_pred = model.predict(X_test)
# 精度の評価
accuracy = accuracy_score(y_test, y_pred)
print(f"モデルの精度: {accuracy:.2f}")
# 分類レポートの表示
print(classification_report(y_test, y_pred))
# 決定木の可視化
plt.figure(figsize=(10, 6))
tree.plot_tree(model, feature_names=['年齢', '収入'], class_names=['いいえ', 'はい'], filled=True)
plt.title("決定木の可視化")
plt.show()モデルの精度: 0.67
precision recall f1-score support
いいえ 0.00 0.00 0.00 0
はい 1.00 0.67 0.80 3
accuracy 0.67 3
macro avg 0.50 0.33 0.40 3
weighted avg 1.00 0.67 0.80 3
回帰木の分岐条件(住宅価格や気温などの数値データの予測)
目的は、連続的な数値を予測することです。今回は気温を予測する例です。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
# サンプルデータの作成
# 特徴量(例:日数)
X = np.array([[1], [2], [3], [4], [5], [6], [7], [8], [9], [10]])
# 対応する気温(例:日ごとの気温)
y = np.array([30, 32, 35, 33, 31, 29, 28, 27, 26, 25])
# 回帰木モデルの作成
model = DecisionTreeRegressor()
# モデルの学習
model.fit(X, y)
# 新しいデータポイントの予測
X_new = np.array([[11], [12], [13]])
predictions = model.predict(X_new)
# 結果の表示
for day, temp in zip(X_new.flatten(), predictions):
print(f"日数: {day}, 予測気温: {temp:.2f}°C")
# 学習データと予測結果の可視化
plt.scatter(X, y, color='blue', label='実際の気温')
plt.scatter(X_new, predictions, color='red', label='予測気温', marker='x')
plt.plot(X, model.predict(X), color='green', label='回帰木の予測')
plt.title("回帰木による気温予測")
plt.xlabel("日数")
plt.ylabel("気温 (°C)")
plt.legend()
plt.show()日数: 11, 予測気温: 25.00°C
日数: 12, 予測気温: 25.00°C
日数: 13, 予測気温: 25.00°C
数理解析と偏微分方程式
数理解析は、連続的な現象を数学的に解析する分野です。機械学習では、最適化問題やモデルの動作理解に利用されます。ここでは、偏微分方程式、ラプラス変換、フーリエ変換について説明します。
偏微分方程式
物理シミュレーションや連続時間モデルでの利用
偏微分方程式(PDE)は、2つ以上の独立変数に依存する関数の偏微分が含まれる方程式です。物理学、工学、経済学、生物学など、多くの分野で現れる現象をモデル化するために使用されます。例えば、熱方程式は温度の変化を、波動方程式は音波や光波の伝播を記述します。
偏微分方程式は主に線形と非線形に分類され、非線形方程式は複雑な現象を表現しますが、解法が難しくなります。解法には、特定の条件下で明示的な解を求める解析的手法と、数値計算を用いて近似解を得る数値的手法があります。
このように、偏微分方程式は自然現象の理解や予測に不可欠な数学的ツールです。
線形偏微分方程式
$$A(x, y) \frac{\partial^2 u}{\partial x^2} + B(x, y) \frac{\partial^2 u}{\partial y^2} + C(x, y) \frac{\partial u}{\partial x} + D(x, y) \frac{\partial u}{\partial y} + E(x, y) u = F(x, y)$$
ここで、$u{(x,y)}$ は未知関数、$A, B, C, D, E, F$ は既知の関数です。
熱伝導方程式
$$\frac{\partial u}{\partial t} = \alpha \nabla^2 u$$
ここで、 $u$ は温度分布、$α$ は熱拡散率、$\nabla^2$ はラプラシアン演算子です。
ラプラシアン演算子とは?:
ラプラシアン演算子(Laplacian operator)は、数学や物理学において重要な役割を果たす微分演算子であり、特に偏微分方程式や多次元解析で広く用いられます。ラプラシアンは、関数の局所的な変化を測定するための指標として使われ、一般的に次のように定義されます。
1次元の場合:$\nabla^2 u(x) = \frac{\partial^2 u}{\partial x^2}$
2次元の場合:$\nabla^2 u(x, y) = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} $
近似式が必要な理由:
近似式は、連続的な関数や物理現象を数値的に解析する際に必要です。実際の問題では、微分方程式を解くための解析解を得ることが難しい場合が多く、数値解析が用いられます。ラプラス演算子の近似式を使用することで、離散的な格子点を用いて関数の変化を表現でき、計算機上でのシミュレーションが可能になります。この方法により、熱伝導や流体力学などの複雑な現象を扱うことができ、実用的な解を得るための手段となります。
一次元の熱伝導方程式の近似式
$\nabla^2 u[i] \approx u[i + 1] – 2u[i] + u[i – 1]$
使用例)
偏微分方程式(PDE)は、物理シミュレーションや連続時間モデルで使用されます。特に、熱伝導、流体力学、電磁気学などのシミュレーションにおいて重要です。
熱伝導方程式の数値解法(有限差分法)
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
L = 10.0 # 長さ
T = 2.0 # 時間
nx = 100 # 空間分割数
nt = 500 # 時間分割数
alpha = 0.01 # 熱拡散率
dx = L / (nx - 1)
dt = T / nt
# 初期条件
u = np.zeros(nx)
u[int(nx/4):int(3*nx/4)] = 100 # 中央部分を高温に設定
# 熱伝導方程式の数値解法
for n in range(nt):
u_new = u.copy()
for i in range(1, nx-1):
# 熱伝導方程式の近似式
u_new[i] = u[i] + alpha * dt / dx**2 * (u[i+1] - 2*u[i] + u[i-1])
u = u_new
# 結果のプロット
x = np.linspace(0, L, nx)
plt.plot(x, u, label='温度分布')
plt.title('熱伝導方程式の数値解')
plt.xlabel('位置 x')
plt.ylabel('温度 u')
plt.legend()
plt.grid(True)
plt.show()
グラフに描かれた曲線は、シミュレーションの最終時間ステップにおける温度分布を示しています。初期条件として中央部分に高温(100度)が設定されているため、グラフの中央付近で温度が高く、周囲に向かって温度が低下している様子が見られます。
ラプラス変換
ラプラス変換は、時間領域の関数 $f(t)$ を複素数領域に変換する手法です。
$$F(s) = \mathcal{L}\{f(t)\} = \int_{0}^{\infty} e^{-st}f(t) dt$$
$s$ は複素数、$t$ は時間です。
使用例)
主に制御理論、信号処理、物理学などの分野で使われ、特に微分方程式の解法において便利です。ラプラス変換により、微分方程式を代数方程式に変換し、容易に解を求めることができます。
特徴)
ラプラス変換は、初期条件を考慮した形で関数を扱えるため、時間に依存するシステムの解析に適しています。また、非定常状態の問題を解決する際にも広く用いられます。
ラプラス変換の実装
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
# ラプラス変換を計算する関数
def laplace_transform(f, s):
"""
ラプラス変換を計算する関数
f: 時間領域の関数
s: ラプラス変換の変数
"""
# ラプラス変換の定義に基づいて積分を計算
result, _ = quad(lambda t: f(t) * np.exp(-s * t), 0, np.inf)
return result
# 時間領域の信号(例:指数関数)
def f(t):
return np.exp(-t) # 例として、f(t) = e^(-t)
# ラプラス変換の変数sの範囲を設定
s_values = np.linspace(0, 5, 100)
laplace_values = [laplace_transform(f, s) for s in s_values]
# 結果のプロット
plt.plot(s_values, laplace_values)
plt.title('ラプラス変換の結果')
plt.xlabel('s')
plt.ylabel('L{f(t)}')
plt.grid(True)
plt.show()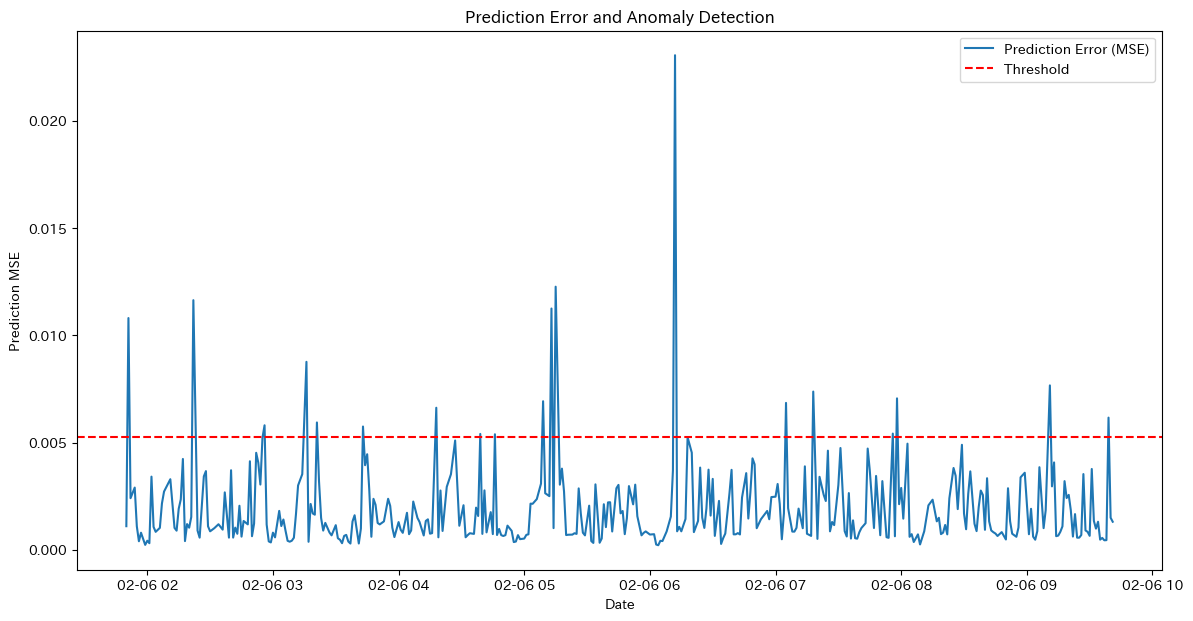
このグラフは、時間領域の信号(この場合は指数関数 $f(t)=e^{−t}$)に対するラプラス変換の結果を示していて、信号の周波数成分やダイナミクスを理解するための重要な情報を提供しています。具体的には、横軸はラプラス変換の変数 $s$ を表し、縦軸はラプラス変換の結果 $L{f(t)}$ を表しています。
フーリエ変換
フーリエ変換は、時間領域の関数 $f(t)$ を周波数領域に変換する手法です。
$$F(\omega) = \mathcal{F}\{f(t)\} = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} \, dt$$
$ω$ は角周波数です。
使用例)
主に信号処理、音響工学、画像処理、振動解析などの分野で使用されます。フーリエ変換により、信号の周波数成分を抽出し、周期的な現象やスペクトル解析を行うことができます。
特徴)
フーリエ変換は、信号を異なる周波数成分に分解し、各成分の振幅と位相を分析できるため、周期的および非周期的な信号の特性を理解するのに適しています。
フーリエ変換の実装
import numpy as np
import matplotlib.pyplot as plt
# サンプル信号の生成
Fs = 500 # サンプリング周波数
T = 1/Fs # サンプリング間隔
L = 500 # サンプル数
t = np.linspace(0, (L-1)*T, L)
# 信号:50Hzと120Hzの正弦波にノイズを加える
S = 0.7*np.sin(2*np.pi*50*t) + 1.0*np.sin(2*np.pi*120*t)
S += 0.5*np.random.randn(L)
# フーリエ変換
Y = np.fft.fft(S)
P2 = np.abs(Y/L)
P1 = P2[:L//2+1]
P1[1:-1] = 2*P1[1:-1]
# 周波数軸の生成
f = Fs*np.arange(0, L//2+1)/L
# 結果のプロット
plt.plot(f, P1)
plt.title('単一側フーリエ変換')
plt.xlabel('周波数 (Hz)')
plt.ylabel('振幅')
plt.grid(True)
plt.show()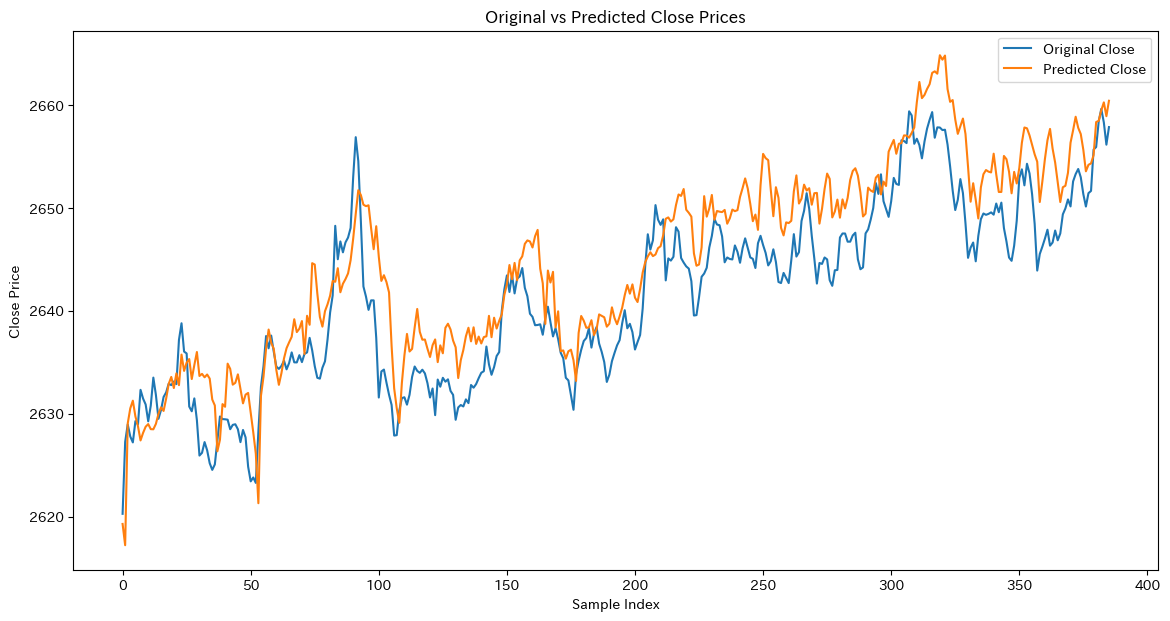
このコードは、50Hzと120Hzの正弦波にノイズを加えた信号を生成し、その信号に対してフーリエ変換を行い、周波数成分をプロットするものです。結果として、信号の周波数成分がどのように分布しているかを視覚的に確認できます。
ラプラス変換とフーリエ変換の比較
| 項目 | ラプラス変換 | フーリエ変換 |
|---|---|---|
| 変換の対象 | 時間領域から複素数領域への変換 | 時間領域から周波数領域への変換 |
| 用途 | 制御理論や微分方程式の解析に重点 | 信号の周波数解析や振動解析に重点 |
| 変数の性質 | 複素数 ( $s$) を用いて、システムの安定性やダイナミクスを解析 | 実数の周波数 ( $\omega$ ) を用いて、周期的な信号の特性を明らかにする |
ラプラス変換とフーリエ変換は、信号を周波数領域に変換する手法です。これらの変換は、信号処理や自然言語処理においてデータの特徴抽出やノイズ除去に利用されます。
フーリエ変換の種類
通常、「フーリエ変換」と言うと、連続フーリエ変換(Continuous Fourier Transform:CFT) と 離散フーリエ変換(Discrete Fourier Transform:DFT) の両方を指す場合があります。
連続フーリエ変換(CFT)
- 連続信号$f(t)$を適用
$$F(\omega) = \mathcal{F} \{ f(t) \} = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt$$
- 時間領域の連続信号 $f(t)$ を、周波数領域の関数 $F(\omega)$ に変換する。
- アナログ信号解析に使用されるが、デジタル処理では離散化が必要。
離散フーリエ変換(DFT)
- デジタル信号(離散データ列)に適用
$$F_k = \sum_{n=0}^{N-1} f_n e^{-i \frac{2\pi kn}{N}}, \quad k = 0,1,\dots, N-1$$
- 有限長の離散データに適用される。
- デジタル信号処理やFFTの基盤となる計算手法。
高速フーリエ変換(FFT)
- FFT(高速フーリエ変換)は、DFT(離散フーリエ変換)の計算を効率化するアルゴリズムです。通常、DFTの計算量は $O(N^2)$ですが、FFTを用いることで $O(N \log N)$に削減できます。
$$F_k = \sum_{n=0}^{N-1} f_n e^{-i \frac{2\pi kn}{N}}, \quad k = 0,1,\dots, N-1$$
通常の計算では、各$F_k$ を求めるのに $O(N)$ の計算が必要で、全体では $O(N^2)$となります。
- FFTの特長
- FFTは、DFTを分割統治法(Divide and Conquer)を用いて再帰的に計算し、計算量を $O(N^2)$から$O(N \log N)$に削減します。
- 大規模データやリアルタイム処理に適しており、高速な信号処理が可能です。
- 画像処理、音声処理、通信分野など、幅広い応用があります。
高速フーリエ変換(FFT)の実装例)
- FFT による音声信号の周波数解析
- 音声ファイル(例: m4a)を読み込み、一部の音声信号に対して離散フーリエ変換(DFT)を適用し、周波数スペクトルを計算・可視化するコード例です。
- デジタル信号処理では、離散化したDFT(FFT)を用いて解析します。
import numpy as np
import matplotlib.pyplot as plt
import librosa
import librosa.display
def load_audio(filename, sr=16000):
"""
音声ファイルを指定したサンプリングレートで読み込む。
"""
y, sr = librosa.load(filename, sr=sr)
return y, sr
def plot_fft_of_audio(y, sr, start_sec=0, duration_sec=1):
"""
音声信号の一部(start_sec から duration_sec 秒間)に対して
離散フーリエ変換を適用し、単一側フーリエ変換のスペクトルをプロットする。
"""
# 対象区間の抽出
start_sample = int(start_sec * sr)
end_sample = int((start_sec + duration_sec) * sr)
y_segment = y[start_sample:end_sample]
L = len(y_segment)
# FFT を実施
Y = np.fft.fft(y_segment)
# 振幅スペクトルの作成
P2 = np.abs(Y) / L
P1 = P2[:L//2+1]
P1[1:-1] = 2 * P1[1:-1]
# 周波数軸の生成
f = sr * np.arange(0, L//2+1) / L
plt.figure(figsize=(10, 5))
plt.plot(f, P1)
plt.title('単一側フーリエ変換')
plt.xlabel('周波数 (Hz)')
plt.ylabel('振幅')
plt.grid(True)
plt.show()
def main():
# 音声ファイルのパス(実際のファイルパスに合わせてください)
audio_file = "音声データのパスを入力"
y, sr = load_audio(audio_file, sr=16000)
print(f"音声長: {len(y)/sr:.2f}秒, サンプリング周波数: {sr} Hz")
# 音声の先頭1秒間を対象として FFT を計算・プロット
plot_fft_of_audio(y, sr, start_sec=0, duration_sec=1)
if __name__ == '__main__':
main()Deprecated as of librosa version 0.10.0.
It will be removed in librosa version 1.0.
y, sr_native = __audioread_load(path, offset, duration, dtype)
音声長: 59.63秒, サンプリング周波数: 16000 Hz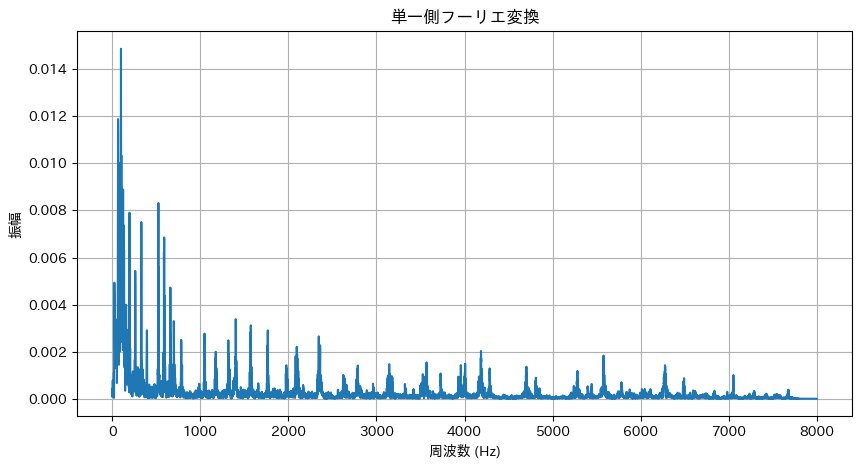
高速フーリエ変換(FFT)は主に音声認識においてMFCC(メル周波数ケプストラム係数)の算出手順に用いられることがあります。
- MFCCについては下記URLを参考にしてください。

離散コサイン変換(DCT)
DCTは、信号を周波数成分に分解する数学的変換 であり、画像圧縮や音声処理で広く活用 されています。フーリエ変換と異なり、実数のみを扱い、エネルギーを効率的に集約できるのが特徴です。
| 特徴 | 説明 |
|---|---|
| エネルギーを低次元に集中 | 高次成分の影響は小さく、少ない係数で信号を近似できるため、データ圧縮やノイズ除去に適している。 |
| 実数のみを扱う(フーリエ変換との違い) | フーリエ変換(DFT)は複素数を含むが、DCTは実数のみで表現可能で、計算コストが低く解釈しやすい。 |
| 信号の対称性を利用 | 偶関数(対称な波形)を基に変換を行うため、DC成分(低周波成分)が明確に表れる。 |
数式)
1D信号 $f(n)$に対するDCT
$$F_k = \sum_{n=0}^{N-1} f_n \cos \left[ \frac{\pi}{N} \left( n + \frac{1}{2} \right) k \right], \quad k = 0,1,\dots, N-1$$
- $f_n$ :入力信号。$F_k$ :DCT係数。$N$ :データの長さ。
- 低い $k$ の成分(低周波成分)が、信号の主要な情報を持つことが多い。
DCTの活用例)
| 活用例 | 説明 |
|---|---|
| 音声処理(MFCCの計算) | メルフィルタバンクの出力にDCTを適用し、MFCC(メル周波数ケプストラム係数)を算出。音声の特徴をコンパクトに表現し、認識精度を向上。 |
| 画像圧縮(JPEG圧縮) | 画像ブロックごとにDCTを適用して高周波成分を抑制。情報量の少ない部分を削減することで、圧縮率を向上させる。 |
| 異常検知・信号処理 | データの周波数特性を分析し、異常検知やフィルタリングに活用。 |
DCTは信号を周波数成分に分解する変換で、実数のみを扱いエネルギーを効率的に集約できるため、データ圧縮や音声処理に有効であり、MFCCによる音声認識やJPEG画像圧縮など幅広い分野で利用されています。
離散コサイン変換(DCT)の実装例)
import numpy as np
import matplotlib.pyplot as plt
import librosa
import librosa.display
from scipy.fft import dct
def load_audio(filename, sr=16000):
"""
指定したサンプリングレートで音声ファイルを読み込む。
"""
y, sr = librosa.load(filename, sr=sr)
return y, sr
def plot_dct_of_audio(y, sr, start_sec=0, duration_sec=1):
"""
音声信号の指定区間(start_secからduration_sec秒間)に対して離散コサイン変換(DCT)を実施し、
そのスペクトル(DCT係数)をプロットする。
注意:
DCT のインデックスと周波数はFFTのように直接対応しない点に留意してください。
"""
# 対象区間のサンプルの抽出
start_sample = int(start_sec * sr)
end_sample = int((start_sec + duration_sec) * sr)
y_segment = y[start_sample:end_sample]
L = len(y_segment)
# DCT の計算(タイプ II, 規格化付き)
dct_coeff = dct(y_segment, type=2, norm='ortho')
# DCTの係数は、信号のエネルギーが低インデックスに集中する傾向があるため、
# その絶対値をプロットする
indices = np.arange(L)
plt.figure(figsize=(10, 5))
plt.plot(indices, np.abs(dct_coeff))
plt.title('離散コサイン変換 (DCT) のスペクトル')
plt.xlabel('DCTインデックス')
plt.ylabel('振幅')
plt.grid(True)
plt.show()
def main():
# 音声ファイルのパス(実際のファイルパスに合わせてください)
audio_file = "/Users/yoshihisashinzaki/Desktop/Python/1-01 Cd1-1.m4a"
y, sr = load_audio(audio_file, sr=16000)
print(f"音声長: {len(y)/sr:.2f}秒, サンプリング周波数: {sr} Hz")
# 音声の先頭1秒間に対して DCT を計算・プロット
plot_dct_of_audio(y, sr, start_sec=0, duration_sec=1)
if __name__ == '__main__':
main()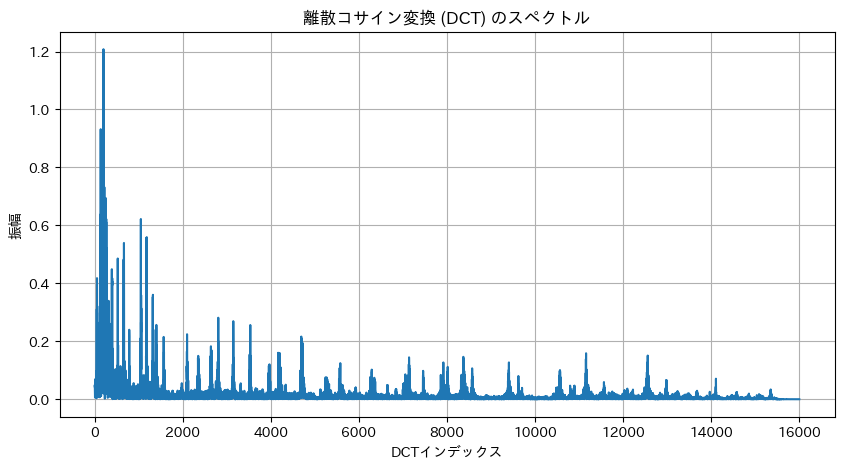
- FFTとの違い
- FFTは複素数の周波数成分(振幅と位相両方)を求めるのに対し、DCTは実数のみのコサイン基底を用いて信号のエネルギー分布を表現します。
| 特徴 | FFT | DCT |
|---|---|---|
| 出力の性質 | 複素数の結果が得られ、正負の周波数成分が対になって現れる。 | 出力は実数のみで、信号のエネルギーが低次元(低インデックス)に集中しやすい。 |
| エネルギーの集中 | エネルギー分布は比較的広範囲に分散する。 | 少数の係数にエネルギーが集中するため、圧縮や特徴抽出(例:MFCCの計算)に有利。 |
| 周波数との対応 | 各係数が明確な周波数成分に直接対応しており、周波数軸に沿った解析が容易。 | インデックスと周波数の対応はFFTほど直接的ではなく、信号のエネルギー分布に着目した解析が行われる。 |
統計的学習理論(Kaggle対策)
統計的学習理論は、学習アルゴリズムの性能を理論的に評価する枠組みです。ここでは、汎化誤差、VC次元、PAC学習について説明します。
汎化誤差
モデルの未学習データに対する精度評価
汎化誤差は、モデルが未知のデータに対してどれだけ正確に予測できるかを示す指標です。汎化誤差を最小化することは、過学習を防ぎ、モデルの実用性を高めるために重要です。
$$汎化誤差=E_{(x,y)∼P}[L(f(x),y)]$$
$L$ は損失関数、 $f$ は学習モデル、 $P$ はデータの真の分布です。
以下に、汎化誤差、VC次元、PAC学習の情報をテーブル形式でまとめました。それぞれの項目を切り離してコピーできるようにしています。
汎化誤差の使い方
| 指標 | 汎化誤差 |
|---|---|
| 分野 | 汎化誤差は、教師あり学習全般において重要な指標です。特に、回帰分析や分類問題で、モデルの未学習データに対する予測精度を評価する際に用いられます。 |
| 応用 | モデルの選択やハイパーパラメータ調整において、過学習を防ぎ、実際のデータに対するモデルの実用性を高めるために利用されます。 |
使用例)
汎化誤差は、モデルが未知のデータに対してどれだけ正確に予測できるかを評価する指標です。クロスバリデーションやテストセットを用いて汎化誤差を推定し、モデルの性能を評価することができます。
決定木を使った交差検証による汎化誤差の推定
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeClassifier
import numpy as np
# データのロード
iris = load_iris()
X, y = iris.data, iris.target
# モデルの定義
model = DecisionTreeClassifier()
# モデルの学習
model.fit(X, y) # ここに学習を追加
# 交差検証(5分割)
scores = cross_val_score(model, X, y, cv=5, scoring='accuracy')
print(f"各分割の精度: {scores}")
print(f"汎化誤差の推定値: {1 - np.mean(scores)}")各分割の精度: [0.96666667 0.96666667 0.9 0.96666667 1. ]
汎化誤差の推定値: 0.039999999999999813from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
# 決定木の可視化
plt.figure(figsize=(10, 6))
plot_tree(model, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.title("決定木の可視化")
plt.show()
# 特徴量の重要度の可視化
importances = model.feature_importances_
plt.bar(iris.feature_names, importances)
plt.title("特徴量の重要度")
plt.xlabel("特徴量")
plt.ylabel("重要度")
plt.show()
# 交差検証の結果の可視化
plt.plot(range(1, 6), scores)
plt.title("交差検証の結果")
plt.xlabel("分割")
plt.ylabel("精度")
plt.show()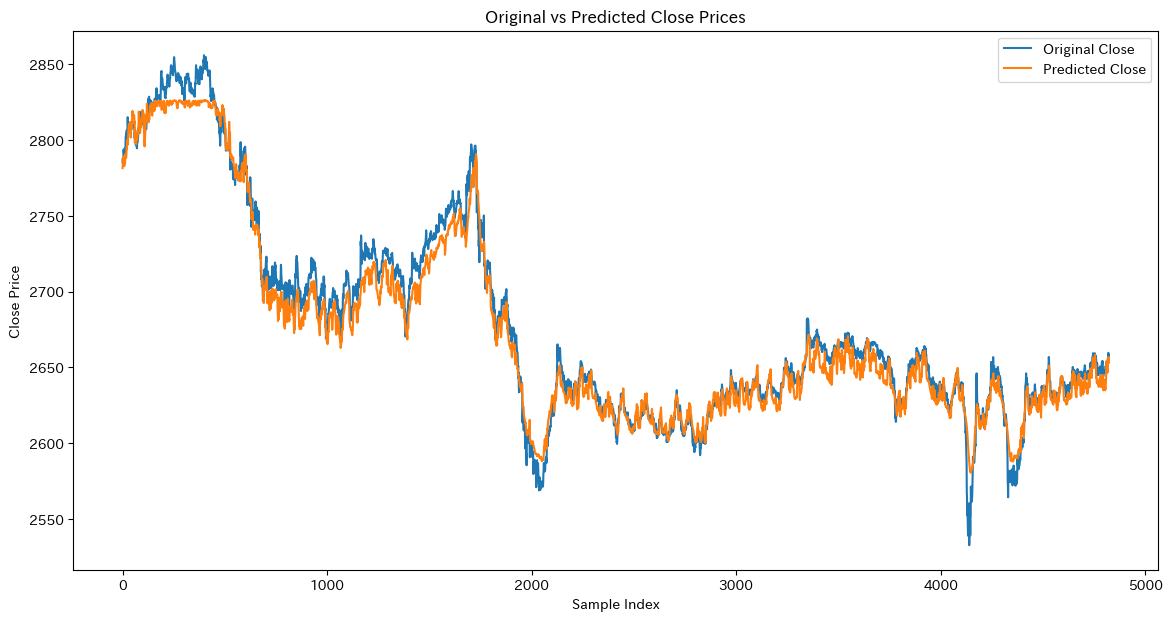

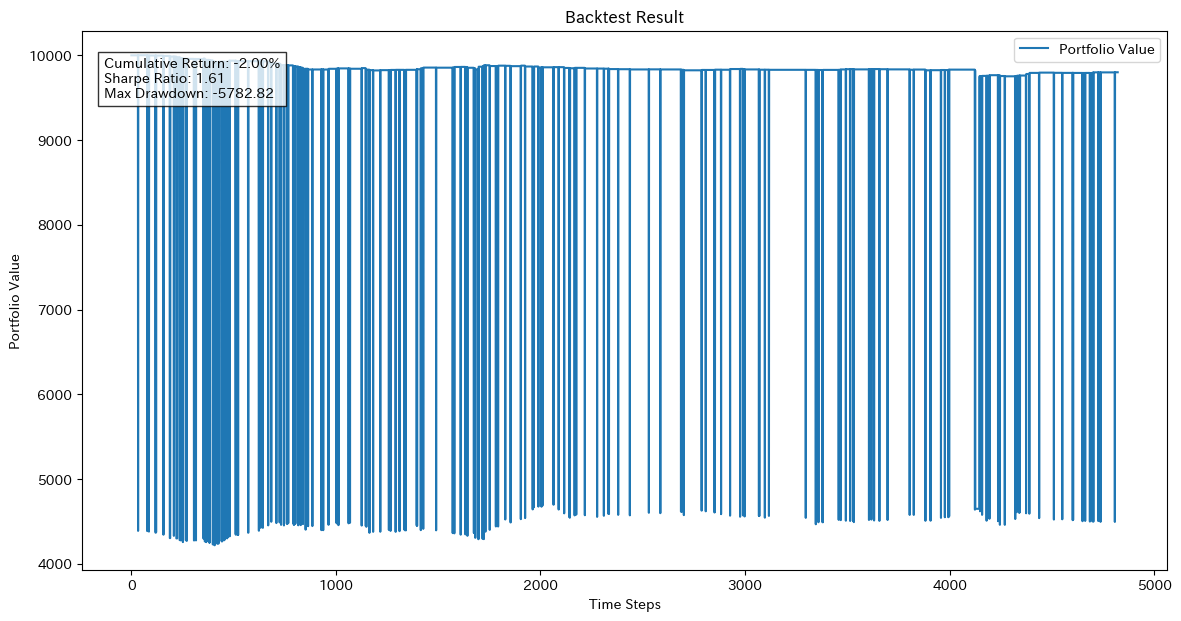
この決定木では、花弁の長さと花弁の幅がルートノードで用いられており、分類に最も重要な特徴量であることがわかります。また、特徴量の棒グラフからもpetal length と petal width の重要度がわかります。交差検証の分割はcv=5の精度が良いことがわかります。
必要な特徴量に絞って再学習
# データのロード
iris = load_iris()
X = iris.data[:, [2, 3]] # petal length (cm)とpetal width (cm)のみを使用
y = iris.target
# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# モデルの定義
model = DecisionTreeClassifier(random_state=42)
# モデルの学習
model.fit(X_train, y_train)
# 交差検証(5分割)
scores = cross_val_score(model, X_train, y_train, cv=5, scoring='accuracy')
print(f"各分割の精度: {scores}")
print(f"汎化誤差の推定値: {1 - np.mean(scores)}")
# テストデータでの精度
y_pred = model.predict(X_test)
accuracy = np.mean(y_pred == y_test)
print(f"テストデータでの精度: {accuracy}")各分割の精度: [0.95238095 0.9047619 0.85714286 0.95238095 0.95238095]
汎化誤差の推定値: 0.07619047619047614
テストデータでの精度: 1.0先ほどよりもモデルの精度も汎化性能の推定値も落ちてはいますが、このモデルの方がより厳密にモデルの精度や汎化誤差に信用性があることがわかります。
モデルが現在のテストデータに対しては1.0と良い結果を出していることを示していますが、それがモデル学習における最大値であるとは限りません。良いモデル学習を行うためには以下のことを改善することでモデルの汎化性能を上げることができます。
| 項目 | 説明 |
|---|---|
| 汎化性能の評価 | テストデータだけでなく、様々なデータセットを用いてモデルの汎化性能を評価する必要があります。 |
| 過学習の防止 | モデルが訓練データに過剰適合しないように、適切な正則化やハイパーパラメータの調整を行う必要があります。 |
| モデルの改善 | 常にモデルの改善を追求し、より高い精度と汎化性能を目指すべきです。 |
| 交差検証の実施 | データを複数のサブセットに分割し、異なるデータでモデルを訓練・評価することで、より信頼性の高い評価を行います。 |
| 特徴量の選択 | 不要な特徴量を除外し、重要な特徴量を選択することで、モデルの性能を向上させます。 |
| データの前処理 | データのスケーリングや欠損値の処理を行い、モデルがより良い入力を受け取れるようにします。 |
| 異常値の処理 | データ内の異常値を特定し、適切に処理することでモデルの精度を向上させます。 |
| アンサンブル学習 | 複数のモデルを組み合わせて予測を行うことで、個々のモデルの弱点を補完し、より良い結果を得ることができます。 |
VC次元
モデルの複雑さや学習可能性の尺度
VC次元(Vapnik-Chervonenkis次元)は、モデルの複雑さや表現能力を測る指標です。VC次元が高いほど、モデルは多様なデータパターンを学習できますが、過学習のリスクも高まります。VC次元はモデルの組み合わせやパラメータの調整によって変わってしまうということです。
データセットを料理に例えると、VC次元は料理の複雑さに相当します。シンプルな食材で作る料理には、シンプルなレシピ(線形モデル)が適しています。複雑な食材を組み合わせた料理には、複雑なレシピ(ニューラルネットワーク)が必要になります。VC次元を考慮することで、データセット(料理)に適したレシピ(アルゴリズム)を選択することができます。
VC次元の定義
VC次元は、ある学習モデルが任意のラベル付け(バイナリラベルやカテゴリラベル)を完全に適合させることができるデータセットの最大サイズを表します。VC次元を問い直すことでデータセットに応じたアルゴリズムの選定やパラメーターのチューニングができるということです。
例)
- 線形モデルはVC次元が低いため、単純なデータセットに適している。
- ニューラルネットワークはVC次元が高く、複雑なデータセットに適している。
定義:モデル $H$ の$VC$次元 $d_{VC}$ は、次の条件を満たす最大の整数 $d$ です。
- 任意の $d$ 個の点からなるデータセットに対して、モデル $H$ はそのデータセットに対するすべての可能なラベル付け(分類)を実現できる。
| アルゴリズム | VC次元の例 | 説明 |
|---|---|---|
| 線形分類器 | ( $d_{VC} = 3$ ) | 2次元空間において、任意の3点が非同一直線上に配置されている場合、その3点に対するすべてのラベル付けを実現できるが、4点の場合はできないことがあります。 |
| ニューラルネットワーク | VC次元はノード数や層数に依存 | ニューラルネットワークのVC次元は、ネットワークの構造により異なり、層やノードが増えるとVC次元も増加し、より複雑なデータパターンを学習可能になりますが、過学習のリスクも高まります。 |
| 決定木 | VC次元は木の深さや分岐数に依存 | 決定木のVC次元は、木の深さやノードの数によって決まり、深い木ほど複雑なデータを学習できますが、深すぎると過学習のリスクが増加します。 |
| サポートベクターマシン(SVM) | VC次元はサポートベクターの数に依存 | SVMのVC次元は、サポートベクターの数と関係があり、複雑な決定境界を形成する能力を示します。サポートベクターが多いほど、モデルの表現能力が高まります。 |
| k-最近傍法(k-NN) | VC次元は使用するデータポイントの数に依存 | k-NNのVC次元は、選択された近傍の数に関連し、選択されるポイントの数が増えると、モデルが学習できるパターンの複雑さが増しますが、計算負荷が高まる場合もあります。 |
使用例)
VC次元は、モデルの複雑さや表現能力を測る指標です。高いVC次元を持つモデルは、多様なデータパターンを学習できますが、過学習のリスクも高まります。モデル選択や正則化の際にVC次元を考慮します。
SVMのマージンとVC次元の関係(概念的説明)
VC次元は理論的な概念であり、直接的な計算は難しいですが、SVM(サポートベクターマシン)のマージンを大きくすることでモデルの複雑さを制御することができます。以下は、マージンの大きさとサポートベクターの数を視覚的に確認する例です。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# データセットのロード
iris = datasets.load_iris()
X = iris.data[:, :2] # 2つの特徴量
y = iris.target
# SVMモデルの定義(マージンの大きさを変更)
C_values = [0.1, 1, 10]
plt.figure(figsize=(15, 4))
for i, C in enumerate(C_values):
clf = svm.SVC(kernel='linear', C=C)
clf.fit(X, y)
# サポートベクターの数
n_sv = clf.n_support_
# プロット
plt.subplot(1, 3, i+1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, edgecolors='k')
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=100, facecolors='none', edgecolors='k', label='Support Vectors')
plt.title(f"SVM with C={C}\nSupport Vectors: {sum(n_sv)}")
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.tight_layout()
plt.show()VC次元はSVCの線形モデルなのでVC次元は特徴量2+1で3です。Cの値を問い直すことでモデルの複雑さや表現を測ることができます。
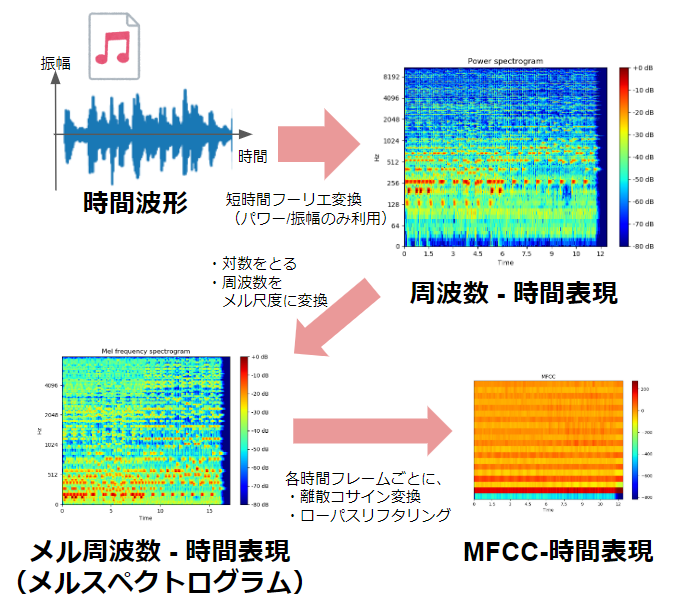
この場合、散布図から、C の値を大きくすると、サポートベクターの数が減少し、決定境界がより複雑になることを確認できます。これは、C の値を大きくすることで、モデルがより複雑になり、訓練データに過剰に適合しようとする傾向があることを示しています。この中ではC=1が最もバランスのいいモデルであるということができるということです。
モデルの組み合わせによってVC次元は変化し、VC次元を問い直すことで過学習のリスクを評価することができます。しかし、VC次元は過学習の指標の一つであり、他の指標も考慮して総合的に判断する必要があります。
また、モデルのハイパーパラメータのチューニングによっても汎化性能を上げることができるため、データセットに応じたVC次元の選び方と同様に重要な選択だと言えます。
選択したアルゴリズムのハイパーパラメーターを問うことは、モデルの複雑さを理解し、データセットの特性に適したアルゴリズムを選択することにつながります。VC次元やハイパーパラメータを考慮することで、過学習を防ぎ、モデルの汎化性能を向上させることができます。
PAC学習
学習アルゴリズムの性能評価枠組み
PAC学習(Probably Approximately Correct Learning)は、学習アルゴリズムが一定の確率で、近似的に正しい仮説を見つけることを保証する枠組みです。PAC学習は、アルゴリズムの効率性や信頼性を評価するために用いられます。
学習アルゴリズムの成功条件
学習アルゴリズムがある仮説 $h$ を生成する際、以下の条件を満たす必要があります。
ε-近似
生成された仮説 $h$ は、真の概念(ターゲット関数) $c$ と十分に近いことが求められます。具体的には、$h$ の誤差が許容範囲 $ϵ$ 以下である必要があります。これは次のように表現されます。
$$\text{err}(h) = \mathbb{P}_{x \sim P} [h(x) \neq c(x)] \leq \epsilon$$
ここで、$err{(h)}$ は仮説 $h$ とターゲット関数 $c$ の誤差率、$P$ はデータの分布、$x$ はサンプルです。
確率δ
アルゴリズムが$ε-$近似に成功する確率は $1−δ$ 以上でなければならない。つまり、アルゴリズムは失敗する確率が $δ$ 以下であることを保証します。
$$\mathbb{P}[\text{err}(h) \leq \epsilon] \geq 1 – \delta$$
サンプル数の理論
PAC学習における重要なポイントは、アルゴリズムが成功するために必要なサンプル数です。サンプル数 $m$ が十分に大きいと、PAC学習アルゴリズムは次の条件を満たします。
サンプル数 $m$ は次のように依存します。
$$m = \mathcal{O} \left( \frac{1}{\epsilon} \log \frac{1}{\delta} \right)$$
ここで、$ϵ$ は許容される誤差、$δ$ は失敗の確率です。つまり、誤差を小さくしたい($ϵ$を小さくする)ほど、より多くのサンプルが必要であり、信頼度を高める($δ$を小さくする)ほど、サンプル数は増加します。
PAC学習の要点
| 項目 | 内容 |
|---|---|
| 定義 | 学習アルゴリズムが、一定の確率で近似的に正しい仮説を見つける理論的枠組み。 |
| 誤差 (ε) | 学習した仮説の誤差が許容範囲内($\epsilon$)であることを保証。 |
| 信頼度 (δ) | 仮説が正しい確率が ($1 – \delta$) 以上であることを保証。 |
| 必要なサンプル数 | 必要なサンプル数は ($m = \mathcal{O}\left(\frac{1}{\epsilon} \log\frac{1}{\delta}\right)$) に従う。 |
| 用途 | 学習アルゴリズムの性能評価と理論的保証。 |
単純なPAC学習のシミュレーション
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
def pac_learning_simulation(n_samples, n_features, n_trials, epsilon, delta):
"""
PAC学習のシミュレーション
n_samples: サンプル数
n_features: 特徴量の数
n_trials: 試行回数
epsilon: 許容誤差
delta: 信頼度
"""
successes = 0 # PAC条件を満たした試行回数
for _ in range(n_trials): # 試行回数をループ
# データの生成
X = np.random.randn(n_samples, n_features) # 特徴量行列 (n_samples x n_features)
true_weights = np.random.randn(n_features) # 真の重み (n_features)
y = (X @ true_weights + np.random.randn(n_samples) * 0.5 > 0).astype(int) # ラベル (n_samples)
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# モデルの学習
model = LogisticRegression()
model.fit(X_train, y_train)
# テストデータでの精度
y_pred = model.predict(X_test)
acc = accuracy_score(y_test, y_pred)
# PAC条件の確認
if acc >= 1 - epsilon: # 正解率が許容誤差以上であれば成功
successes += 1
probability = successes / n_trials
print(f"成功確率: {probability}")
if probability >= 1 - delta:
print("PAC条件を満たしています。")
else:
print("PAC条件を満たしていません。")
# 例:シミュレーションの実行
pac_learning_simulation(n_samples=100, n_features=10, n_trials=100, epsilon=0.1, delta=0.05)成功確率: 0.72
PAC条件を満たしていません。シミュレーション結果がPAC条件を満たさない場合、それは、この例で使用されているロジスティック回帰モデルが、この特定のデータセットと設定されたパラメータに対して、信頼性の低いモデルである可能性を示唆しています。つまり、未知のデータに対して、高い確率で高い精度で予測できるとは限らないということです。
注意点
- データセットのランダム性:このコードで生成されるデータセットはランダムです。そのため、シミュレーション結果もランダムに変化します。
- パラメータの影響:epsilon と delta の値も、PAC学習の条件に影響を与えます。これらの値を厳しく設定すると、PAC条件を満たすのが難しくなります。
この例に対する改善点
- 異なるデータセット:異なるデータセットでシミュレーションを実行し、ロジスティック回帰の性能を評価する。
- 異なるアルゴリズム:他のアルゴリズム(例えば、SVM、決定木など)でシミュレーションを実行し、比較する。
- ハイパーパラメータのチューニング:ロジスティック回帰のハイパーパラメータをチューニングし、PAC学習の条件を満たせるかどうかを確認する。
モデルを改善させてPAC学習を再度実行してみる
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.model_selection import RandomizedSearchCV
import random
def pac_learning_simulation(n_samples, n_features, n_trials, epsilon, delta, model_type, random_state=None):
"""
PAC学習のシミュレーション
Args:
n_samples (int): データセットのサンプル数。
n_features (int): 各サンプルの特徴量の数。
n_trials (int): 試行回数。
epsilon (float): 許容誤差。
delta (float): 信頼度。
model_type (str): 使用するモデルの種類 ('svm' or 'logistic')
random_state (int, optional): 乱数のシード。デフォルトはNone。
"""
successes = 0 # PAC条件を満たした試行回数
for _ in range(n_trials):
# データの生成(線形分離可能なデータ)
X = np.random.randn(n_samples, n_features)
true_weights = np.random.randn(n_features)
y = (X @ true_weights > 0).astype(int) # 線形分離可能なデータ
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=random_state)
# モデルの選択とハイパーパラメータチューニング
if model_type == 'svm':
model = SVC(kernel='rbf')
param_distributions = {'C': np.logspace(-2, 2, 5), 'gamma': np.logspace(-2, 2, 5)}
elif model_type == 'logistic':
model = LogisticRegression(max_iter=1000)
param_distributions = {'C': np.logspace(-2, 2, 5)}
else:
raise ValueError("model_type must be 'svm' or 'logistic'")
random_search = RandomizedSearchCV(model, param_distributions, n_iter=20, cv=5, random_state=random_state)
random_search.fit(X_train, y_train)
best_model = random_search.best_estimator_
# テストデータでの精度
y_pred = best_model.predict(X_test)
acc = accuracy_score(y_test, y_pred)
# PAC条件の確認
if acc >= 1 - epsilon:
successes += 1
# PAC条件を満たす確率を計算
probability = successes / n_trials
print(f"成功確率: {probability}")
# PAC条件を満たしているか確認
if probability >= 1 - delta:
print("PAC条件を満たしています。")
else:
print("PAC条件を満たしていません。")
# シミュレーションの実行
n_samples = 500 # サンプル数
n_features = 10 # 特徴量の数
n_trials = 100 # 試行回数
epsilon = 0.1 # 許容誤差
delta = 0.05 # 信頼度
model_type = 'svm' # 使用するモデルの種類 ('svm' or 'logistic')
random_state = 42 # 乱数のシード
pac_learning_simulation(n_samples, n_features, n_trials, epsilon, delta, model_type, random_state)成功確率: 1.0
PAC条件を満たしています。今回はPAC条件を満たすことができました。PAC学習の条件を満たすには試行錯誤してみる必要があるので、是非チャレンジしてみましょう。
その他の特殊分野(Kaggle対策:改善の余地あり)
機械学習の応用範囲は広く、様々な数学の特殊分野が関連しています。ここでは、微分幾何学、確率過程、ガウス過程について説明します。
微分幾何学
ニューラルネットワークの理論研究への応用
微分幾何学は、曲線や曲面の性質を研究する数学の分野です。ニューラルネットワークの最適化や可視化において、微分幾何学の概念が応用されます。例えば、パラメータ空間の幾何学的構造を理解することで、より効率的な最適化手法の開発が可能となります。
パラメータ空間と接線ベクトル
ニューラルネットワークでは、学習中にモデルのパラメータ(重み)を更新します。ネットワークのパラメータ空間は高次元で複雑ですが、微分幾何学を使うことで、これらのパラメータ空間を解析することができます。
- パラメータ空間の幾何学的構造:
ネットワークのパラメータ空間は、ニューラルネットワークの学習過程で重要な役割を果たします。各パラメータは、モデルの学習における変化や更新を定義します。微分幾何学では、パラメータ空間の点を曲線として表現し、接線ベクトル(勾配)を使ってその方向を示します。
曲率と最適化
ニューラルネットワークにおける最適化問題では、パラメータ空間における曲率(曲がり具合)が非常に重要です。曲率が大きい場所では、勾配降下法などの最適化手法で収束速度が遅くなる可能性があります。逆に、曲率が小さい場所では、最適化が早く進む場合があります。
曲率の定義:
- パラメータ空間の曲率は、二階微分によって測定されます。曲率が大きい場所では、損失関数が急激に変化するため、最適化アルゴリズムはその方向で学習を進めます。曲率が小さい場所では、学習が遅くなることがあり、最適化の効率に影響を与えます。
曲率を測るためには、ヘッセ行列(損失関数の二階偏微分行列)を使用します。
$$H(w)=∇^2L(w)$$
ここで、$H(w)$ はヘッセ行列であり、パラメータ空間の曲率を表します。最適化アルゴリズム(例えば、ニュートン法)では、このヘッセ行列を利用して、更新方向を調整し、効率的に収束させます。
自然勾配法とリーマン計量
リーマン計量は、パラメータ空間の「距離」を定義するための概念です。自然勾配法は、通常の勾配法(勾配降下法)を改善する方法であり、リーマン計量を使用して、パラメータ空間の局所的な幾何学的構造に基づいて勾配を調整します。これにより、より効率的に最適解に近づくことができます。
- リーマン計量と自然勾配法:リーマン計量を用いて、勾配を次のように修正します。
$$v_{\text{natural}} = G(w)^{-1} \nabla_w L(w)$$
ここで、$G(w)$ はパラメータ空間のリーマン計量を表す行列です。この計量を使うことで、最適化が異なるスケールや曲率を持つ方向に対して適切に調整され、より効率的な学習が可能になります。
可視化と最適化の進行
円の曲線に関する微分幾何学的特性は、ニューラルネットワークの最適化過程におけるパラメータ空間の曲線や曲面の理解に直接関連しています。例えば、モデルのパラメータ空間における最適化の進行を可視化する際に、微分幾何学の概念を利用して、パラメータ更新の方向や曲率を視覚的に理解することができます。
簡単な曲線の微分幾何学的特性の計算
import numpy as np
import matplotlib.pyplot as plt
# 曲線のパラメータ化(例:円)
theta = np.linspace(0, 2*np.pi, 100)
x = np.cos(theta)
y = np.sin(theta)
# 接線ベクトルの計算
dx = -np.sin(theta)
dy = np.cos(theta)
# 曲率の計算
curvature = np.abs(dx * np.gradient(dy) - dy * np.gradient(dx)) / (dx**2 + dy**2)**1.5
# 結果のプロット
plt.figure(figsize=(8, 6))
plt.plot(x, y, label='円')
plt.quiver(x, y, dx, dy, curvature, cmap='viridis', label='接線ベクトルと曲率')
plt.colorbar(label='曲率')
plt.title('円の微分幾何学的特性')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.axis('equal')
plt.grid(True)
plt.show()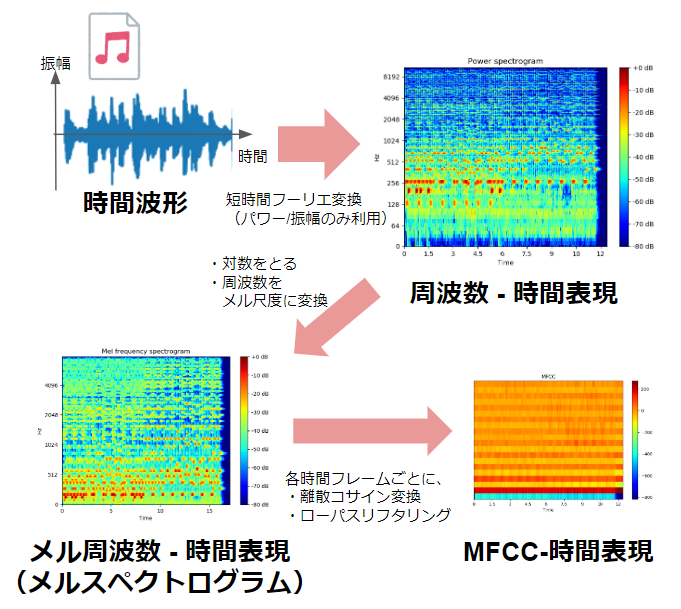
このコードは、微分幾何学における基本的な概念である曲率を、視覚的に理解するためのものです。円は、すべての点で曲率が一定の曲線です。このコードを実行すると、円の各点における接線ベクトルと曲率がグラフ上に表示され、曲率が円周全体で一定であることが確認できます。
自然勾配法の開発と応用例
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
# リーマン計量を計算する関数
def compute_riemannian_metric(parameters):
# ここでは、単純な例として対角行列のリーマン計量を計算
# 実際のアプリケーションでは、タスクやモデル構造に合わせた計量を計算する必要があります
num_parameters = sum(p.numel() for p in parameters)
metric = torch.diag(torch.tensor([1.0] * num_parameters))
return metric
# 自然勾配法を計算する関数
def natural_gradient(loss, parameters, learning_rate):
# リーマン計量を計算
metric = compute_riemannian_metric(parameters)
# 勾配を計算
gradients = torch.autograd.grad(loss, parameters, create_graph=True)
# 自然勾配を計算
flat_gradients = torch.cat([g.flatten() for g in gradients])
natural_gradients = torch.linalg.solve(metric, flat_gradients)
# パラメータを更新
offset = 0
for param in parameters:
numel = param.numel()
param.data -= learning_rate * natural_gradients[offset:offset + numel].reshape(param.shape)
offset += numel
# ニューラルネットワークの定義
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(1, 10)
self.fc2 = nn.Linear(10, 1)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = self.fc2(x)
return x
# データセットの生成
x_train = torch.randn(100, 1)
y_train = 2 * x_train + torch.randn(100, 1)
# モデルの定義
model = Net()
# 学習ループ
epochs = 100
losses = []
learning_rate = 0.1 # 初期学習率
decay_rate = 0.95 # 学習率の減衰率
for epoch in range(epochs):
# 学習率の更新
learning_rate *= decay_rate
# 勾配の初期化
optimizer.zero_grad()
# 予測値の計算
outputs = model(x_train)
# 損失関数の計算
loss = nn.MSELoss()(outputs, y_train)
# 損失関数の逆伝播
loss.backward(retain_graph=True) # retain_graph=True を設定
# パラメータの更新
params = list(model.parameters()) # model.parameters()をリストに格納
natural_gradient(loss, params, 0.01) # 自然勾配法
losses.append(loss.item())
# 学習結果のプロット
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('学習結果')
plt.show()
このコードは、微分幾何学の概念を用いて、より効率的な最適化手法を開発しようとする試みであり、その目的を達成する可能性を秘めています。以下はその可能性に対する課題です。
- より複雑なリーマン計量を導入する。
- 計算コストを削減する手法を開発する。
- 様々なタスクやモデル構造に対して、自然勾配法の効果を検証する。
ニューラルネットワークの理論研究への応用の探究
パラメータ空間の幾何学的構造の理解
ニューラルネットワークのパラメータは高次元空間に存在し、複雑な幾何学的構造を持ちます。学習は、この空間上を最適解に向かって移動する過程として捉えられます。
| 方法 | 内容 |
|---|---|
| 曲率の可視化 | パラメータ空間の曲率を可視化することで、学習が困難な領域を特定し、その領域における最適化の改善策を講じることができます。 |
| 最適化アルゴリズムの改善 | パラメータ空間の幾何学的構造を考慮し、最適化アルゴリズムを改善することで、学習の効率を向上させ、新しいアルゴリズムを開発することができます。 |
応用例
- 画像認識:画像認識タスクにおいて、パラメータ空間の曲率を可視化することで、学習が困難な領域を特定し、学習アルゴリズムを改善することができます。
- 自然言語処理:自然言語処理タスクにおいて、パラメータ空間の曲率を可視化することで、学習が困難な領域を特定し、学習アルゴリズムを改善することができます。
活性化関数の設計
活性化関数は、ニューラルネットワークの非線形性を導入する重要な要素です。活性化関数の形状は、ニューラルネットワークの表現能力に影響を与えます。微分幾何学の概念を用いることで、活性化関数の形状を設計し、ニューラルネットワークの表現能力を向上させることができます。
| 応用例 | 内容 |
|---|---|
| 活性化関数の曲率を制御 | 活性化関数の曲率を制御することで、ニューラルネットワークの学習過程を安定化させ、最適化を効率化します。 |
| 微分幾何学に基づいた新しい活性化関数の設計 | 微分幾何学を用いて、ニューラルネットワークの表現能力を高める新しい活性化関数を設計し、学習性能を向上させます。 |
モデルの汎化性能の向上
ニューラルネットワークの汎化性能とは、未知のデータに対する予測精度のことです。汎化性能を向上させるためには、モデルの複雑さを適切に制御する必要があります。微分幾何学の概念を用いることで、モデルの複雑さを制御し、汎化性能を向上させることができます。
| 応用例 | 内容 |
|---|---|
| モデルの曲率を制御 | モデルの曲率を制御することで、過学習を防ぎ、汎化性能を向上させ、未知のデータに対する予測精度を改善します。 |
| 微分幾何学に基づいた正則化手法の開発 | 微分幾何学の概念を利用して、モデルの複雑さを適切に制御するための新しい正則化手法を開発し、汎化性能を向上させます。 |
確率過程
時系列データの解析方法(例:マルコフ連鎖)
確率過程は、時間とともに変化する確率変数の集合です。時系列データの解析において、マルコフ連鎖などの確率過程が用いられます。マルコフ連鎖は、現在の状態が過去の状態に依存せず、現在の状態のみから次の状態が決定される特性を持ちます。
マルコフ連鎖の定義
$$P(X_{n+1} = x | X_n = x_n, \dots, X_0 = x_0) = P(X_{n+1} = x | X_n = x_n)$$
使用例)
確率過程は、時間とともに変化する確率変数の集合を扱います。時系列データの解析や予測(例:株価の予測、天気予報)において、マルコフ連鎖などのモデルが使用されます。
マルコフ連鎖のシミュレーション
import numpy as np
import matplotlib.pyplot as plt
def simulate_markov_chain(transition_matrix, states, start_state, n_steps):
"""
マルコフ連鎖をシミュレートする関数
transition_matrix: 状態遷移行列
states: 状態のリスト
start_state: 初期状態
n_steps: シミュレーションのステップ数
"""
current_state = start_state
state_sequence = [current_state]
for _ in range(n_steps):
current_index = states.index(current_state)
probabilities = transition_matrix[current_index]
current_state = np.random.choice(states, p=probabilities)
state_sequence.append(current_state)
return state_sequence
# 例:天気モデル(晴れ、曇り、雨)
states = ['晴れ', '曇り', '雨']
transition_matrix = [
[0.8, 0.15, 0.05], # 晴れから
[0.2, 0.6, 0.2], # 曇りから
[0.3, 0.3, 0.4] # 雨から
]
# シミュレーションの実行
sequence = simulate_markov_chain(transition_matrix, states, '晴れ', 30)
# 結果のプロット
plt.figure(figsize=(12, 2))
plt.plot(range(len(sequence)), [states.index(s) for s in sequence], marker='o')
plt.yticks(range(len(states)), states)
plt.xlabel('時間ステップ')
plt.ylabel('状態')
plt.title('マルコフ連鎖による天気のシミュレーション')
plt.grid(True)
plt.show()
このコードは、マルコフ連鎖と呼ばれる確率的なモデルをシミュレートし、その結果をグラフで可視化しています。具体的には、天気予報のような、ある時点の状態が過去の状態にのみ依存し、未来の状態に影響を与えるモデルを例とすることができます。
ガウス過程
ベイズ的機械学習モデルの基礎
ガウス過程は、無限次元の確率分布であり、関数の分布をモデル化します。ベイズ的機械学習では、ガウス過程を用いて予測の不確実性を評価します。ガウス過程回帰は、観測データに基づいて関数の予測分布を求める手法で、機械学習において強力なツールとして活用されています。
ガウス過程の定義
$$f(x) \sim \text{GP}(m(x), k(x, x’))$$
- $m(x)$ は平均関数で、入力 $x$ に対する関数値の平均を表します。
- $k(x, x’)$ は共分散関数、またはカーネル関数で、入力 $x$ と $x′$ に対する関数値の共分散を表します。
任意の有限個の入力点 $x_1,x_2,…,x_n$に対して、対応する関数値 $f(x_1),f(x_2),…,f(x_n)$ は多変量正規分布に従います。
$$\begin{pmatrix}
f(x_1) \\
f(x_2) \\
\vdots \\
f(x_n)
\end{pmatrix}
\sim \mathcal{N} \left(
\begin{pmatrix}
m(x_1) \\
m(x_2) \\
\vdots \\
m(x_n)
\end{pmatrix}
,
\begin{pmatrix}
k(x_1, x_1) & k(x_1, x_2) & \cdots & k(x_1, x_n) \\
k(x_2, x_1) & k(x_2, x_2) & \cdots & k(x_2, x_n) \\
\vdots & \vdots & \ddots & \vdots \\
k(x_n, x_1) & k(x_n, x_2) & \cdots & k(x_n, x_n)
\end{pmatrix}
\right)$$
このように、ガウス過程は関数の全体的な振る舞いを捉えることができ、各点での関数値がどのように相関しているかをカーネル関数を通じてモデル化します。
使用例)
ガウス過程は、ベイズ的機械学習モデルの基礎として使用されます。特に、回帰問題において、予測の不確実性を評価するために利用されます。ガウス過程回帰は、観測データに基づいて関数の予測分布を求める手法です。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C
# トレーニングデータの生成
X_train = np.array([[1], [3], [5], [6], [7], [8]])
y_train = np.sin(X_train).ravel()
# テストデータの生成
X_test = np.linspace(0, 10, 100).reshape(-1, 1)
# カーネルの定義
kernel = C(1.0, (1e-3, 1e3)) * RBF(1.0, (1e-2, 1e2))
# ガウス過程回帰モデルの定義と学習
gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)
gp.fit(X_train, y_train)
# 予測と不確実性の計算
y_pred, sigma = gp.predict(X_test, return_std=True)
# 結果のプロット
plt.figure(figsize=(10, 6))
plt.plot(X_train, y_train, 'ro', label='トレーニングデータ')
plt.plot(X_test, y_pred, 'b-', label='予測')
plt.fill_between(X_test.ravel(), y_pred - 1.96*sigma, y_pred + 1.96*sigma,
alpha=0.2, color='blue', label='95% 信頼区間')
plt.title('ガウス過程回帰の例')
plt.xlabel('入力 x')
plt.ylabel('出力 y')
plt.legend()
plt.grid(True)
plt.show()
y_pred # 予測値array([ 0.59429605, 0.62476599, 0.65477757, 0.68406673, 0.71234948,
0.73932297, 0.76466697, 0.78804587, 0.80911108, 0.82750397,
0.84285936, 0.85480949, 0.86298858, 0.86703786, 0.86661109,
0.86138055, 0.85104333, 0.83532796, 0.81400124, 0.78687508,
0.75381332, 0.71473835, 0.66963732, 0.61856787, 0.56166309,sigma # 予測値の標準偏差:予測値のばらつきarray([0.35461934, 0.3157147 , 0.27658798, 0.23757407, 0.19902271,
0.16129249, 0.12474437, 0.08973475, 0.0566082 , 0.02569016,
0.00272037, 0.02835766, 0.05099603, 0.07045543, 0.08660659,
0.09937487, 0.10874308, 0.11475291, 0.11750493, 0.1171572 ,
0.11392229, 0.10806298, 0.09988643, 0.0897372 , 0.07798917,sigma が大きいほど、予測値のばらつきが大きく、予測値の不確実性が高いことを意味します。
3つの回帰アルゴリズムの比較
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
# データの生成
def f(x):
return np.sin(0.9 * x) + 0.1 * x
np.random.seed(0)
X_train = np.random.uniform(-5, 5, size=10).reshape(-1, 1)
y_train = f(X_train).ravel() + np.random.normal(0, 0.2, size=10) # 修正箇所
X_test = np.linspace(-5, 5, 100).reshape(-1, 1)
y_test = f(X_test)
# ガウス過程回帰
kernel = RBF()
gp = GaussianProcessRegressor(kernel=kernel)
gp.fit(X_train, y_train)
y_pred_gp, sigma_gp = gp.predict(X_test, return_std=True)
# 線形回帰
lr = LinearRegression()
lr.fit(X_train, y_train)
y_pred_lr = lr.predict(X_test)
# サポートベクター回帰
svr = SVR(kernel='rbf')
svr.fit(X_train, y_train)
y_pred_svr = svr.predict(X_test)
# 結果のプロット
plt.figure(figsize=(12, 6))
plt.plot(X_test, y_test, 'k-', label='真の関数')
plt.plot(X_train, y_train, 'ro', label='トレーニングデータ')
plt.plot(X_test, y_pred_gp, 'b-', label='ガウス過程回帰')
plt.fill_between(X_test.ravel(), y_pred_gp - 1.96 * sigma_gp, y_pred_gp + 1.96 * sigma_gp,
color='b', alpha=0.2, label='95% 信頼区間')
plt.plot(X_test, y_pred_lr, 'g-', label='線形回帰')
plt.plot(X_test, y_pred_svr, 'r-', label='サポートベクター回帰')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()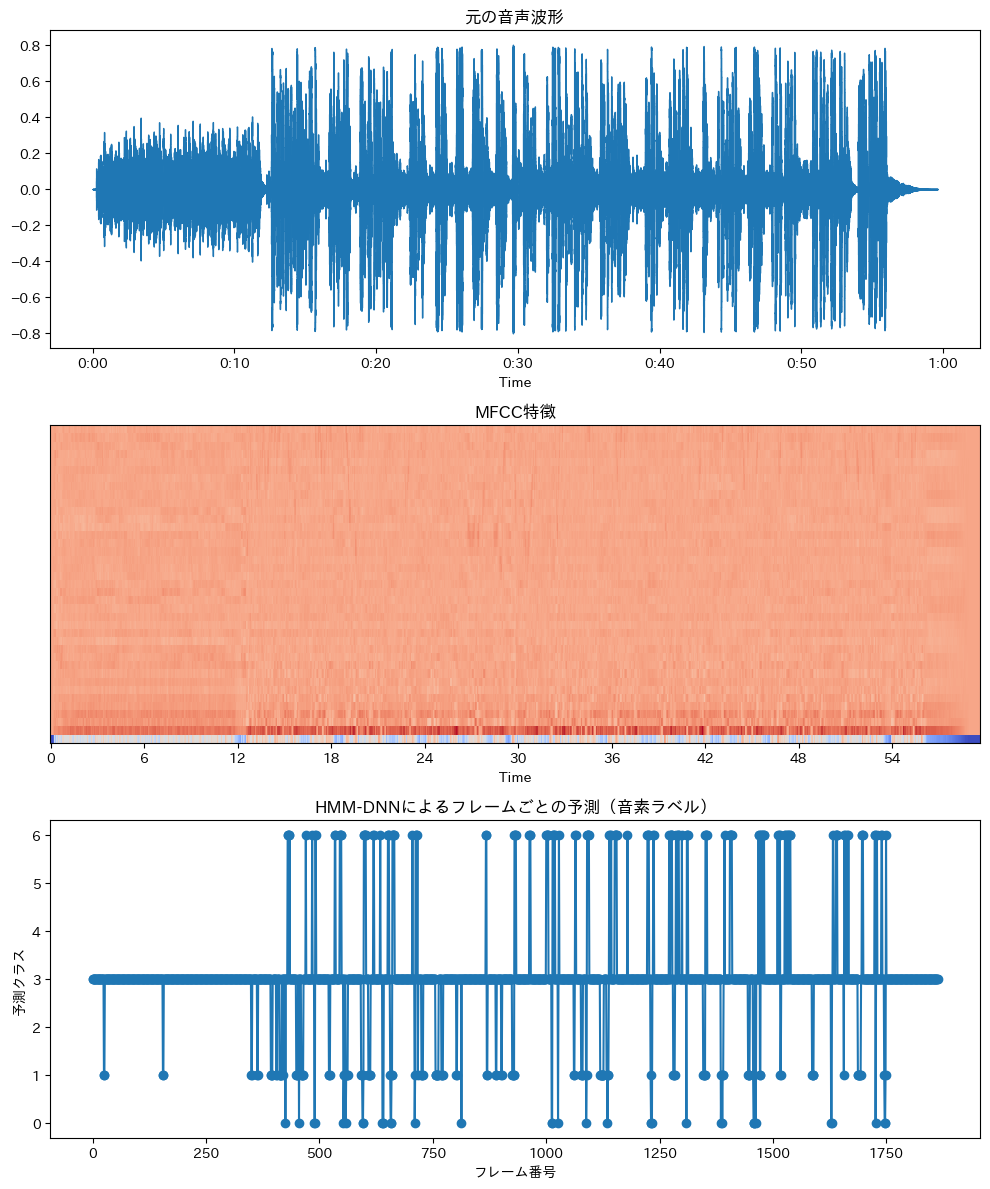
このコードは、異なる回帰アルゴリズムの予測性能を比較することを目的としています。特に、ガウス過程回帰が、他の回帰アルゴリズムと比べて、非線形な関数の予測や予測値の不確実性の推定において優れていることを示しています。
学習の振り返り
今回のブログでは、情報理論や高度な数学概念が機械学習に与える影響を深く掘り下げ、理論的な基盤から実践的な応用に至るまで幅広く学びました。情報理論では、データの不確実性を測るエントロピーや、モデルの性能評価に使われるKLダイバージェンス、相互情報量などの概念が機械学習の精度向上にどのように貢献するかを学びました。また、離散数学、数理解析、統計的学習理論といった分野も、アルゴリズムの理論的支柱として機能し、最適化や汎化性能、学習アルゴリズムの性能評価に不可欠であることを理解しました。
さらに、微分幾何学や確率過程、ガウス過程などの特殊分野は、ニューラルネットワークや時系列解析において強力なツールを提供し、学習の効率化やデータの解釈力を高めるために欠かせない知識です。
全3回にわたる数学シリーズを通じて、機械学習を支える数学的な基盤を深く理解し、理論と実践の橋渡しができたことを嬉しく思います。この知識をもとに、今後の機械学習の研究や応用に役立てていただければと思います。




コメント