【第5回】モデル評価と最適化（後編）

目的

このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用できる力を養うことが目的です。この過程で、実践的な演習やプロジェクトを通じて、手を動かしながら学ぶ姿勢を大切にしていきます。

第5回の目標

第5回の目標は、機械学習モデルの評価と最適化に関する技術を深く理解し、実践的なスキルを身につけることです。具体的には、モデルの性能を正確に評価するための各種モデルの指標（精度、適合率、再現率、F1スコア、AUC-ROC曲線、平均二乗誤差）の定義や適用例を学ぶことで、評価基準の重要性を理解します。また、交差検証の技術を習得し、K分割交差検証やLeave-One-Out交差検証を通じてモデルの汎化性能を評価し、過学習を防ぐ方法をマスターします。さらに、ハイパーパラメータの最適化手法であるグリッドサーチ、ランダムサーチ、ベイズ最適化を実践することで、モデル性能の最大化に向けた能力を養います。過学習を防ぐための正則化やドロップアウトなどの技術についても理解を深め、アンサンブル学習を通じて複数のモデルを組み合わせる方法を学ぶことで、高い予測性能を実現します。これにより、Kaggleコンペティションにおいて競争力のあるモデルを構築し、実践的なデータ解析スキルを向上させることを目指します。

前編では分類、回帰、交差検証などのモデル評価を扱った回になりましたが、後編では様々なモデルの最適化を扱った回になりますのでよろしくお願いします。

ハイパーパラメータチューニング

ハイパーパラメータチューニングは、機械学習モデルの性能を最大化するための重要なプロセスです。モデルの学習過程において、ハイパーパラメータは事前に設定される値であり、モデルの構造や学習過程に大きな影響を与えます。例えば、決定木の深さやサポートベクターマシンのカーネル関数の選択、ニューラルネットワークの隠れ層の数などがハイパーパラメータに該当します。

ハイパーパラメータチューニングの重要性

モデルの性能向上：

適切に設定されたハイパーパラメータは、モデルの精度や汎化能力を向上させるため、訓練データに対する適合度を高めます。

過学習の防止：

不適切なハイパーパラメータ設定は、モデルが訓練データに過度に適合し、未知のデータに対する性能が低下する過学習を引き起こす可能性があります。

最適化の必要性：

ハイパーパラメータは、学習アルゴリズムがどのようにデータを扱うかを定義するため、その最適化は機械学習のプロセスにおいて不可欠です。

グリッドサーチ (Grid Search)

グリッドサーチは、事前に指定したハイパーパラメータの組み合わせをすべて試して最適なものを見つける方法です。このアプローチはシンプルで、全ての組み合わせを網羅するため、最適なハイパーパラメータを確実に見つけることができます。ただし、計算コストが高くなる可能性があります。

from sklearn.model_selection import GridSearchCV, train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import pandas as pd

# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv")  

# 前処理
# 欠損値の処理
imputer = SimpleImputer(strategy='mean')
numerical_cols = df.select_dtypes(include=np.number).columns
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数の処理
categorical_cols = df.select_dtypes(include='object').columns
ohe = OneHotEncoder(handle_unknown='ignore', sparse_output=False)
encoded_data = ohe.fit_transform(df[categorical_cols])
encoded_df = pd.DataFrame(encoded_data, columns=ohe.get_feature_names_out(categorical_cols))
df = pd.concat([df, encoded_df], axis=1)
df = df.drop(categorical_cols, axis=1)

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ランダムフォレストモデルの作成
model = RandomForestClassifier()

# ハイパーパラメータのグリッド
param_grid = {
    'n_estimators': [100, 200],
    'max_depth': [5, 10],
}

# グリッドサーチの実行
grid_search = GridSearchCV(model, param_grid, cv=3)
grid_search.fit(X_train, y_train)

# 最適なハイパーパラメータの取得
best_params = grid_search.best_params_

# 最適なハイパーパラメータの出力
print(f"Best Parameters: {grid_search.best_params_}") 

# 最適なハイパーパラメータを用いたモデルの学習
best_model = RandomForestClassifier(**best_params)
best_model.fit(X_train, y_train)

# テストデータで予測
y_pred = best_model.predict(X_test)

# 正解率の算出
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}") 

出力：

Best Parameters: {'max_depth': 10, 'n_estimators': 200}
Accuracy: 0.78

このコードでは、param_grid に、n_estimators の候補値として [100, 200]、max_depth の候補値として [5, 10] を指定しています。ランダムフォレストモデルの n_estimators と max_depth のハイパーパラメータをグリッドサーチでチューニングし、最適なハイパーパラメータを使ってモデル学習を行い、予測値から正解率を算出しています。

ランダムサーチ (Random Search)

ランダムサーチは、指定した範囲内のハイパーパラメータの組み合わせをランダムに選択して試す方法です。このアプローチは、特に広範なパラメータ空間を探索する場合に有効で、計算コストを抑えつつも良好な結果を得やすいです。

from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import numpy as np
import pandas as pd

# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv")  

# 前処理
# 欠損値の処理
imputer = SimpleImputer(strategy='mean')
numerical_cols = df.select_dtypes(include=np.number).columns
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数の処理
categorical_cols = df.select_dtypes(include='object').columns
ohe = OneHotEncoder(handle_unknown='ignore', sparse_output=False)
encoded_data = ohe.fit_transform(df[categorical_cols])
encoded_df = pd.DataFrame(encoded_data, columns=ohe.get_feature_names_out(categorical_cols))
df = pd.concat([df, encoded_df], axis=1)
df = df.drop(categorical_cols, axis=1)

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ランダムフォレストモデルの作成
model = RandomForestClassifier()

# ハイパーパラメータの分布
param_dist = {
    'n_estimators': randint(100, 500),
    'max_depth': randint(5, 15),
}

# ランダムサーチの実行回数
num_runs = 5

# ランダムサーチの実行と結果の格納
best_params_list = []
for i in range(num_runs):
    random_search = RandomizedSearchCV(model, param_dist, n_iter=10, cv=3)
    random_search.fit(X_train, y_train)
    best_params_list.append(random_search.best_params_)

# 各実行結果の平均化（例：n_estimators の平均）
average_n_estimators = np.mean([params['n_estimators'] for params in best_params_list])
average_max_depth = np.mean([params['max_depth'] for params in best_params_list])

# 平均化したハイパーパラメータを出力
print(f"平均化した最適なハイパーパラメータ:")
print(f"- n_estimators: {int(average_n_estimators)}")
print(f"- max_depth: {int(average_max_depth)}") 

# 平均化したハイパーパラメータを用いたモデルの学習
best_model = RandomForestClassifier(n_estimators=int(average_n_estimators), max_depth=int(average_max_depth)) 
best_model.fit(X_train, y_train)

# テストデータで予測
y_pred = best_model.predict(X_test)

# 正解率の算出
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}") 

出力：

平均化した最適なハイパーパラメータ:
- n_estimators: 395
- max_depth: 13
Accuracy: 0.78

ランダムサーチでは、探索空間からランダムにサンプルするため、実行するたびに異なる最適なハイパーパラメータが得られる可能性があります。そのため、複数回実行して結果を平均化することで、より安定した、そしてより確実な最適解を得られる可能性が高まります。

手法	説明
グリッドサーチ	指定したハイパーパラメータのすべての組み合わせを探索します。
	すべての組み合わせを網羅的に探索するため、最適なハイパーパラメータが見つかりやすいです。
	探索する組み合わせが多くなると、計算時間が長くなる可能性があります。
ランダムサーチ	指定したハイパーパラメータの範囲から、ランダムに組み合わせをサンプリングして探索します。
	すべての組み合わせを探索するわけではないため、計算時間が短くなる可能性があります。
	最適なハイパーパラメータが見つからない可能性もあります。

どちらを使うべきか：

• 探索するハイパーパラメータの数が少ない場合や、最適なハイパーパラメータを確実に探し出す必要がある場合は、グリッドサーチが適しています。
• 探索するハイパーパラメータの数が多く、計算時間を短縮したい場合は、ランダムサーチが適しています。

ベイズ最適化 (Bayesian Optimization)

ベイズ最適化は、ハイパーパラメータチューニングにおいて非常に効率的な手法です。このアプローチは、過去の評価結果を活用して、次に試すべきハイパーパラメータを選択することで、探索の効率を高めます。特に、評価が高コスト（時間や計算資源がかかる）の場合に効果的です。

ベイズ最適化の基本概念

ステップ	説明
代理モデルの構築	ベイズ最適化は、まず代理モデル（通常はガウス過程）を構築します。このモデルは、ハイパーパラメータの組み合わせに対する目的関数の予測を行います。
	代理モデルは、過去の評価結果をもとに、ハイパーパラメータ空間を探索するための基準を提供します。
獲得関数 (Acquisition Function)	獲得関数は、次に試すべきパラメータを決定するための関数です。代理モデルが提供する情報を利用して、探索と利用のトレードオフを考慮します。
	Expected Improvement (EI): 現在の最良スコアを超える期待値を計算し、その値が高いポイントを優先的に探索します。
	Upper Confidence Bound (UCB): モデルの予測に基づき、予測の不確実性を考慮しながら次のポイントを選択します。
反復プロセス	ベイズ最適化は反復的なプロセスです。まず代理モデルを使用して獲得関数を最適化し、新しいハイパーパラメータを選択します。
	その後、新たに選んだハイパーパラメータでモデルを評価し、得られた結果を代理モデルに追加します。このプロセスを繰り返すことで、ハイパーパラメータの最適化を行います。

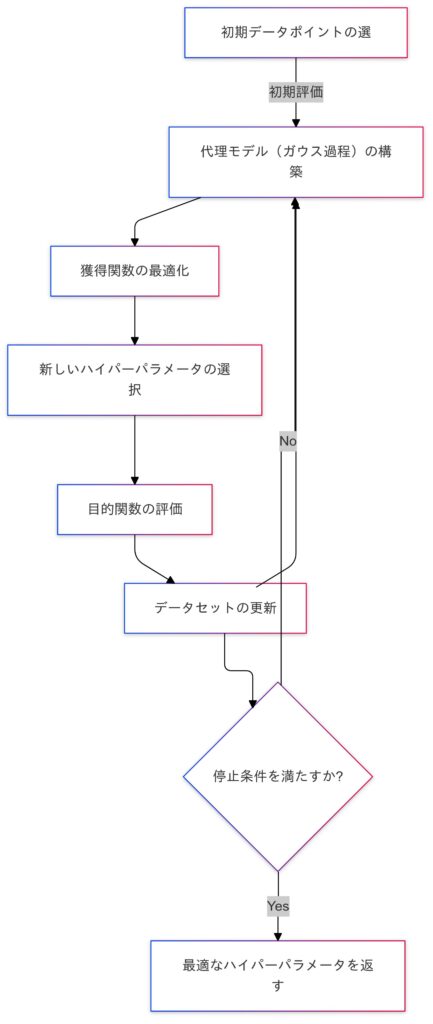
ベイズ最適化の利点

利点	説明
効率的な探索	過去の評価結果を利用するため、ハイパーパラメータ空間を効率的に探索し、少ない試行回数で良い結果を得やすいです。
高コストな評価に最適	モデルの評価が高コストな場合（例：訓練時間が長い）、ベイズ最適化は非常に効果的です。
不確実性の管理	獲得関数を通じて不確実性を考慮するため、安定した結果を得ることが可能です。
複雑な探索空間への対応	ハイパーパラメータの探索空間が複雑な場合でも、ベイズ最適化は効果的に探索を行うことができます。

上記を踏まえるとベイズの最適化の手法はグリッドサーチやランダムサーチよりも少ない試行回数で、最適なハイパーパラメータを見つけることができます。

from bayes_opt import BayesianOptimization
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import pandas as pd


# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv")  # データファイルのパスを指定してください

# 前処理
# 欠損値の処理
imputer = SimpleImputer(strategy='mean')
numerical_cols = df.select_dtypes(include=np.number).columns
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数の処理
categorical_cols = df.select_dtypes(include='object').columns
ohe = OneHotEncoder(handle_unknown='ignore', sparse_output=False)
encoded_data = ohe.fit_transform(df[categorical_cols])
encoded_df = pd.DataFrame(encoded_data, columns=ohe.get_feature_names_out(categorical_cols))
df = pd.concat([df, encoded_df], axis=1)
df = df.drop(categorical_cols, axis=1)

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# モデルの評価を行う関数
def rf_cv(n_estimators, max_depth):
    model = RandomForestClassifier(
        n_estimators=int(n_estimators),
        max_depth=int(max_depth),
    )
    scores = cross_val_score(model, X_train, y_train, cv=3)
    return scores.mean()


# ハイパーパラメータの範囲を設定（n_estimators（決定木の数）と max_depth（木の最大深さ）
pbounds = {
    'n_estimators': (100, 500),
    'max_depth': (5, 15),
}


# ベイズ最適化の初期化
optimizer = BayesianOptimization(
    f=rf_cv,
    pbounds=pbounds,
    random_state=42,
)


# 最適化の実行
optimizer.maximize(init_points=2, n_iter=5)


# 最良のハイパーパラメータを表示
print(f"Best Parameters: {optimizer.max['params']}") 

出力：

このコードはタイタニックデータを使ってランダムフォレストモデルで生存予測を行う際に、ベイズ最適化を使って最適なハイパーパラメータを自動的に見つけることです。

|   iter    |  target   | max_depth | n_esti... |
-------------------------------------------------
| 1         | 0.7682    | 8.745     | 480.3     |
| 2         | 0.802     | 12.32     | 339.5     |
| 3         | 0.7935    | 11.43     | 340.4     |
| 4         | 0.8006    | 14.37     | 337.2     |
| 5         | 0.8034    | 10.33     | 335.2     |
| 6         | 0.7837    | 10.68     | 330.1     |
| 7         | 0.7247    | 6.248     | 336.1     |
=================================================
Best Parameters: {'max_depth': 10.332845916687308, 'n_estimators': 335.15756328697347}

過学習の防止

過学習は、機械学習モデルが訓練データに過度に適合し、未知のデータに対する汎化性能が低下する現象です。これを防ぐためには、正則化やドロップアウトといった技術を利用します。以下では、正則化の3つの手法（L1正則化、L2正則化、Elastic Net）とドロップアウトについて詳しく説明します。

正則化 (Regularization)

正則化は、モデルが過学習を起こさないように、訓練データに対する適合度を調整する手法です。主に以下の3つの手法があります。

LassoやRidgeのような正則化は、回帰モデルに非常に有効です。特に、特徴量が多い場合や、データに多重共線性がある場合に効果を発揮します。

正則化が必要なケース

• 過学習の抑制
• 特徴量選択
• 多重共線性の解消

L1正則化 (Lasso回帰)

L1正則化では、モデルのコスト関数に重みの絶対値の和（L1ノルム）をペナルティとして加えます。このペナルティにより、一部の特徴量の重みが0に近づき、結果として特徴量の選択が容易になり、重要でない特徴量を除外することでモデルの解釈性を向上させます。

$$J(\theta) = L(y, \hat{y}) + \lambda \sum_{j=1}^{n} |\theta_j|$$

$L$は損失関数、$\lambda$は正則化パラメータ、$\theta_j$ はモデルの重みです。

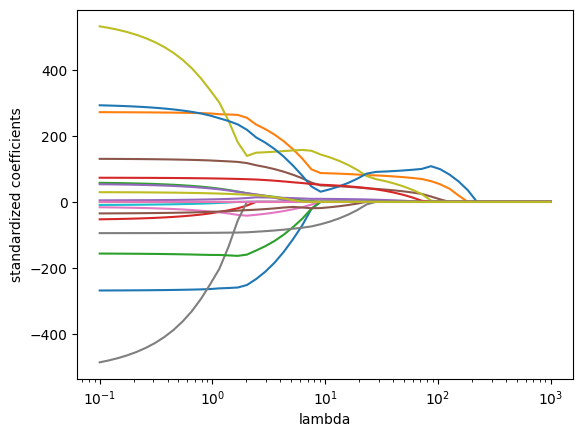
Lassoは最終的に特徴量の重みが0に近づくため、特徴量の選択がしやすくなります。

from sklearn.linear_model import Lasso, LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder, StandardScaler  
import pandas as pd
import numpy as np

# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv") 

# 前処理
# 欠損値の処理
imputer = SimpleImputer(strategy='mean')
numerical_cols = df.select_dtypes(include=np.number).columns
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数の処理
categorical_cols = df.select_dtypes(include='object').columns
ohe = OneHotEncoder(handle_unknown='ignore', sparse_output=False)
encoded_data = ohe.fit_transform(df[categorical_cols])
encoded_df = pd.DataFrame(encoded_data, columns=ohe.get_feature_names_out(categorical_cols))
df = pd.concat([df, encoded_df], axis=1)
df = df.drop(categorical_cols, axis=1)

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# 標準化
scaler = StandardScaler()
X = scaler.fit_transform(X)  # 標準化の実行

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Lasso回帰モデルの作成と学習
lasso = Lasso(alpha=0.1)  # alphaは正則化パラメータ
lasso.fit(X_train, y_train)

# テストデータで予測
y_pred = lasso.predict(X_test)

# MSEで評価
mse = mean_squared_error(y_test, y_pred)
print(f"MSE: {mse:.2f}") 

出力：

MSE: 0.17

L2正則化 (Ridge回帰)

L2正則化では、モデルのコスト関数に重みの二乗の和をペナルティとして加えます。このペナルティにより、重みが全体的に小さく保たれ、過学習を防ぎます。すべての特徴量を使用しつつ重みを抑えることで、モデルの汎化能力を向上させ、特徴量を除外することなく過学習を抑制します。

$$J(\theta) = L(y, \hat{y}) + \lambda \sum_{j=1}^{n} \theta_j^2$$

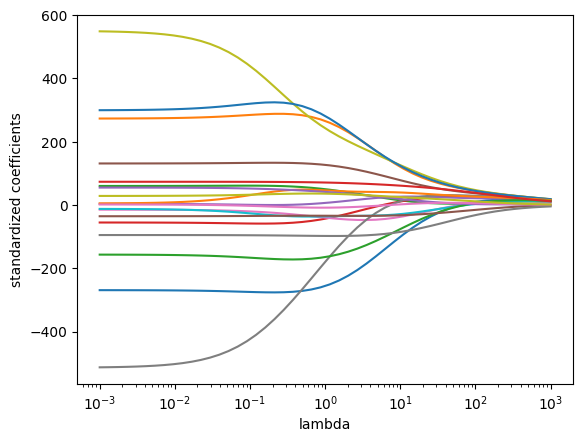
Ridegeはすべての特徴量を使用しつつ重みを抑えることで、モデルの汎化能力を狙い、特徴量を外すことなく過学習を抑えます。

from sklearn.linear_model import Ridge, LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder, StandardScaler
import pandas as pd
import numpy as np

# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv")

# 前処理
# 欠損値の処理
imputer = SimpleImputer(strategy='mean')
numerical_cols = df.select_dtypes(include=np.number).columns
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数の処理
categorical_cols = df.select_dtypes(include='object').columns
ohe = OneHotEncoder(handle_unknown='ignore', sparse_output=False)
encoded_data = ohe.fit_transform(df[categorical_cols])
encoded_df = pd.DataFrame(encoded_data, columns=ohe.get_feature_names_out(categorical_cols))
df = pd.concat([df, encoded_df], axis=1)
df = df.drop(categorical_cols, axis=1)

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# 標準化
scaler = StandardScaler()
X = scaler.fit_transform(X)  # 標準化の実行

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Ridge回帰モデルの作成と学習
Ridge = Ridge(alpha=0.1)  # alphaは正則化パラメータ
Ridge.fit(X_train, y_train)

# テストデータで予測
y_pred = Ridge.predict(X_test)

# MSEで評価
mse = mean_squared_error(y_test, y_pred)
print(f"MSE: {mse:.2f}")

出力：

MSE: 0.15

Ridge正則化の効果を確認

# ridgeによりバリアンスを下げることで係数の値を小さくし、モデルにおける過学習を避けることができる）
lr = LinearRegression()
Ridge.coef_

array([ 0.00276905, -0.03265222, -0.01842757, ...,  0.00044284,
       -0.01139623,  0.0046335 ])

# 正則化項なしの線形回帰と比較（正則化項の線形回帰よりも係数の値が大きい、すなわちvarianceが大きいことを意味する。
lr.fit(X_train, y_train)
lr.coef_

array([-0.01341003, -0.03023027, -0.01058125, ..., -0.00072177,
       -0.01146015,  0.00442608])

Elastic Net

Elastic Netは、L1正則化とL2正則化の組み合わせです。この手法は、Lassoの特徴選択機能とRidgeの安定性の両方を兼ね備えています。データに対して非常に効果的であり、特に多重共線性（相関の強い特徴量が存在する場合）があるときに有用です。

$$J(\theta) = L(y, \hat{y}) + \lambda_1 \sum_{j=1}^{n} |\theta_j| + \lambda_2 \sum_{j=1}^{n} \theta_j^2$$

from sklearn.model_selection import cross_val_score
from sklearn.linear_model import ElasticNet

# Elastic Net回帰
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)

# 交差検定
mse_scores = cross_val_score(elastic_net, X_train, y_train, cv=5, scoring='neg_mean_squared_error')
mse = -np.mean(mse_scores)

print(f"MSE: {mse:.2f}")

# 係数の確認
elastic_net.fit(X_train, y_train)
print("回帰係数:")
print(elastic_net.coef_) 

出力：

MSE: 0.16
回帰係数:
[ 0.         -0.05873628 -0.         ...  0.         -0.
  0.        ]

from sklearn.linear_model import ElasticNet
import numpy as np
from sklearn.metrics import mean_squared_error

# alphaの値を変化させてMSEと回帰係数を記録
alphas = np.logspace(-3, 1)
mse_list = []
coefs = []

for alpha in alphas:
    model = ElasticNet(alpha=alpha, l1_ratio=0.5)  # ElasticNetクラスのインスタンスを生成
    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)
    mse = mean_squared_error(y_test, y_pred)
    mse_list.append(mse)
    coefs.append(model.coef_) 

min_mse_index = np.argmin(mse_list)
optimal_lambda_2 = alphas[min_mse_index]
min_mse = mse_list[min_mse_index]  # 最小MSEも取得
print(f"最適なλ: {optimal_lambda_2:.2f}, 最小MSE: {min_mse:.2f}")

最適なλ: 0.04, 最小MSE: 0.14

ドロップアウト (Dropout)

ドロップアウトは、ニューラルネットワークにおいて過学習を防ぐための技術です。ドロップアウトは、ランダムにニューロンを無効にすることで、モデルが特定のニューロンに依存せず、より強力な特徴を学習できるようにします。これにより、過学習を防ぎ、モデルの汎化能力を向上させることができます。

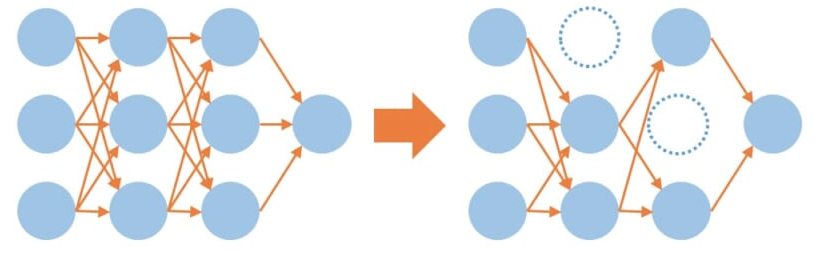
特徴

特徴	説明
目的	ニューラルネットワークの過学習を防ぎ、汎化性能を向上させるための正則化手法です。
有効性	タイタニックデータセットのような比較的少ないデータ量で学習を行う場合、特に有効です。
手法	各訓練のイテレーションで一定の確率（例：50%）でノードを無効にします。
効果	ネットワークが特定のノードに依存せず、より一般化された特徴を学習することを促進します。
表現力	ネットワークの表現力を高め、過学習を防ぐ効果があります。

ドロップアウト確率：

• 各ニューロンが無効化される確率を $p$ とします。例えば、$p=0.5$と設定すると、50%の確率でニューロンが無効化されます。

出力の変化：

• 訓練中、ニューロンの出力 $h_i$ に対して、次のように変化させます。

$$h_i’ = h_i \cdot \text{Bernoulli}(p)$$

ここで、$\text{Bernoulli}(p$)は、確率 $p$ で0を返し、$1−p$ で1を返す関数です。つまり、無効化されると出力が0になります。

推論時のスケーリング：

• 推論時には、すべてのニューロンがアクティブになるため、出力は次のようにスケーリングされます

$$h_i’ = h_i \cdot \frac{1 – p}{1}$$

これにより、訓練時に無効化されたニューロンの影響を調整します。

tensorflowとkerasを使ったニューラルネットワークの実装

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout
from tensorflow.keras.utils import to_categorical
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import pandas as pd
import numpy as np

# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv")

# 前処理（例として、一部の前処理のみ記載）
# 欠損値の処理
df['Age'].fillna(df['Age'].mean(), inplace=True)
df['Embarked'].fillna(df['Embarked'].mode()[0], inplace=True)

# カテゴリカル変数のOne-Hotエンコーディング
df = pd.get_dummies(df, columns=['Sex', 'Embarked', 'Pclass'])

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# 数値データのみを含むように絞り込み
numerical_cols = X.select_dtypes(include=np.number).columns
X_num = X[numerical_cols]

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X_num, y, test_size=0.2, random_state=42)

# 標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 目的変数をone-hotエンコーディング
y_train = to_categorical(y_train, num_classes=2)
y_test = to_categorical(y_test, num_classes=2)

# 入力次元数と出力次元数
input_dim = X_train.shape[1]
num_classes = 2

# モデルの構築
model = Sequential([
    Dense(64, activation='relu', input_shape=(input_dim,)),
    Dropout(0.5),  # 50%の確率でノードを無効化
    Dense(64, activation='relu'),
    Dropout(0.5),
    Dense(num_classes, activation='softmax'),
])

# モデルのコンパイル
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

# モデルの学習
model.fit(X_train, y_train, epochs=50, batch_size=32, validation_data=(X_test, y_test))

# モデルの評価
loss, accuracy = model.evaluate(X_test, y_test)
print(f"Loss: {loss:.4f}, Accuracy: {accuracy:.4f}") 

PyTorchを使ったニューラルネットワークの実装

import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score

# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv")

# 前処理（例として、一部の前処理のみ記載）
# 欠損値の処理
df['Age'].fillna(df['Age'].mean(), inplace=True)
df['Embarked'].fillna(df['Embarked'].mode()[0], inplace=True)

# カテゴリカル変数のOne-Hotエンコーディング
df = pd.get_dummies(df, columns=['Sex', 'Embarked', 'Pclass'])

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# 数値データのみを含むように絞り込み
numerical_cols = X.select_dtypes(include=np.number).columns
X_num = X[numerical_cols]

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X_num, y, test_size=0.2, random_state=42)

# 標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)


# PyTorchのDatasetを作成
class TitanicDataset(Dataset):
    def __init__(self, X, y):
        self.X = torch.tensor(X, dtype=torch.float32)
        self.y = torch.tensor(y.values, dtype=torch.long)  # yをNumPy配列に変換

    def __len__(self):
        return len(self.X)

    def __getitem__(self, idx):
        return self.X[idx], self.y[idx]


# データセットとDataLoaderの作成
train_dataset = TitanicDataset(X_train, y_train)
test_dataset = TitanicDataset(X_test, y_test)
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)


# ニューラルネットワークモデルの定義
class NeuralNetwork(nn.Module):
    def __init__(self, input_size):
        super(NeuralNetwork, self).__init__()
        self.fc1 = nn.Linear(input_size, 64)
        self.relu = nn.ReLU()
        self.dropout = nn.Dropout(0.5)
        self.fc2 = nn.Linear(64, 64)
        self.fc3 = nn.Linear(64, 2)  # 出力層は2クラス分類

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.dropout(x)
        x = self.fc2(x)
        x = self.relu(x)
        x = self.fc3(x)
        return x


# モデル、オプティマイザ、損失関数の定義
model = NeuralNetwork(input_size=X_train.shape[1])
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters())

# モデルの学習
epochs = 50
for epoch in range(epochs):
    for batch_idx, (data, target) in enumerate(train_loader):
        optimizer.zero_grad()
        output = model(data)
        loss = criterion(output, target)
        loss.backward()
        optimizer.step()

    print(f"Epoch [{epoch+1}/{epochs}]")

# モデルの評価
y_pred_list = []
with torch.no_grad():
    for data, target in test_loader:
        output = model(data)
        _, predicted = torch.max(output.data, 1)
        y_pred_list.extend(predicted.tolist())

accuracy = accuracy_score(y_test, y_pred_list)
print(f"Accuracy: {accuracy:.4f}")

このコードの例では隠れ層にDropout層を挿入することで、ニューロンの50%がランダムにドロップアウトします。これにより、モデルの過学習を抑制し、汎化性能を向上させる効果が期待できます。

タイタニックデータセットのような比較的少ないデータ量で学習を行う場合、ドロップアウトの手法は特に有効です。

アンサンブル学習

アンサンブル学習は、複数の機械学習モデルを組み合わせてより高精度な予測を行う手法です。このアプローチは、個々のモデルが持つ弱点を補完し、全体の性能を向上させることを目的としています。アンサンブル学習は、主に「バギング」と「ブースティング」の2つの手法に分類されます。

バギング (Bagging)

バギングは、訓練データのサブセットを使用して複数のモデルを独立に訓練し、それらの予測結果を平均化する手法です。この方法により、モデルのバリアンスを減少させ、過学習を防ぐ効果があります。

$$\hat{y} = \frac{1}{M} \sum_{m=1}^{M} h_m(x)$$

$\hat{y}​$ は最終的な予測値。$M$ は訓練したモデルの数。$h_m(x)$ は第 $m$ 番目のモデルによる予測。

バギングの例）ランダムフォレスト：

ランダムフォレストは、バギングの一種であり、複数の決定木を訓練し、それらの結果を平均化します。さらに、各決定木の訓練時にはランダムに選ばれた特徴量のサブセットを使用することで、決定木同士の相関を減少させ、モデルの汎化性能を向上させます。

特徴	説明
予測精度の向上	複数の決定木を用いることで、単一の決定木よりも予測精度が向上する傾向があります。
過学習の抑制	異なる訓練データで学習された決定木を組み合わせることで、特定の訓練データに過度に適合してしまうのを防ぎます。
頑健性の向上	個々の決定木がノイズの影響を受けやすい場合でも、複数の決定木を組み合わせることで、ノイズの影響を軽減できます。

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
from sklearn.ensemble import RandomForestClassifier
import pandas as pd
import numpy as np

# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv")

# 前処理（例として、一部の前処理のみ記載）
# 欠損値の処理
df['Age'].fillna(df['Age'].mean(), inplace=True)
df['Embarked'].fillna(df['Embarked'].mode()[0], inplace=True)

# カテゴリカル変数のOne-Hotエンコーディング
df = pd.get_dummies(df, columns=['Sex', 'Embarked', 'Pclass'])

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# 数値データのみを含むように絞り込み
numerical_cols = X.select_dtypes(include=np.number).columns
X_num = X[numerical_cols]

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X_num, y, test_size=0.2, random_state=42)

# 標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# ランダムフォレストモデルの作成
model = RandomForestClassifier(n_estimators=100)
model.fit(X_train, y_train)

# テストデータで予測
y_pred = model.predict(X_test)

# 正解率の算出
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}") 

上記のコードでは、RandomForestClassifier を使用することで、バギングによるアンサンブル学習が実装されています。バギングは、複数の学習器を生成し、それらの予測結果を統合することで、予測精度を向上させ、過学習を抑制する効果があります。

様々なバギング手法

バギングは、基本的に異なるサンプルを用いて複数のモデルを訓練し、それらの結果を組み合わせる手法であり、様々なアルゴリズムに応じて応用されています。

バギング手法	説明
Bagged Decision Trees	バギングの基本的なアプローチとして、複数の決定木をバギング手法で訓練し、その結果を平均化または多数決で集約します。ランダムフォレストがこのアプローチを進化させた形です。
Bagging Regressor	回帰問題に対するバギング手法です。複数の回帰モデル（例：決定木回帰器）を使用し、それぞれのモデルの予測結果を平均化します。
Bagged SVM	サポートベクターマシン（SVM）を用いたバギング手法です。異なるサブセットで訓練された複数のSVMを使用し、その結果を組み合わせて最終的な予測を行います。
Bagged k-NN	k-NNアルゴリズムを使用したバギングのアプローチです。異なるサブセットを用いて複数のk-NNモデルを訓練し、それぞれの予測を集約します。
Generalized Bagging	バギングは決定木だけでなく、さまざまなモデルに適用できる一般的な手法です。例えば、ニューラルネットワークやその他の機械学習アルゴリズムにも適用可能です。

Bagged Decision Trees

バギングでは複数の決定木を訓練し、平均化や多数決で結果を集約します。ランダムフォレストはこの手法を改良したものです。

from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier

# バギングの設定
bagging_model = BaggingClassifier(estimator=DecisionTreeClassifier(),
                                   n_estimators=50,
                                   random_state=42)

# モデルの訓練
bagging_model.fit(X_train, y_train)

# テストデータで予測
y_pred = model.predict(X_test)

# 正解率の算出
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}") 

Bagging Regressor

回帰問題におけるバギングでは、複数の回帰モデル（例：決定木回帰器）の予測を平均化します。

from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error

# バギングの設定
bagging_regressor = BaggingRegressor(estimator=DecisionTreeRegressor(),
                                      n_estimators=50,
                                      random_state=42)

# モデルの訓練
bagging_regressor.fit(X_train, y_train)

# テストデータで予測
y_pred = model.predict(X_test)

# 平均二乗誤差の算出
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}") 

Bagged SVM

サポートベクターマシン（SVM）を用いたバギングでは、異なるサブセットで訓練した複数のSVMの結果を組み合わせて予測します。

from sklearn.ensemble import BaggingClassifier
from sklearn.svm import SVC

# バギングの設定
bagging_svm = BaggingClassifier(estimator=SVC(probability=True),
                                 n_estimators=50,
                                 random_state=42)

# モデルの訓練
bagging_svm.fit(X_train, y_train)

# テストデータで予測
y_pred = model.predict(X_test)

# 正解率の算出
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}") 

Bagged k-NN

k-NNアルゴリズムのバギングでは、異なるサブセットで複数のk-NNモデルを訓練し、予測を集約します。

from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier

# バギングの設定
bagging_knn = BaggingClassifier(estimator=KNeighborsClassifier(),
                                 n_estimators=50,
                                 random_state=42)

# モデルの訓練
bagging_knn.fit(X_train, y_train)

# テストデータで予測
y_pred = model.predict(X_test)

# 正解率の算出
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}") 

Generalized Bagging

バギングは決定木だけでなく、ニューラルネットワークや他の機械学習アルゴリズムにも適用できる一般的な手法です。

線形回帰の場合：

from sklearn.ensemble import BaggingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import mean_squared_error

# バギングの設定
generalized_bagging = BaggingClassifier(estimator=LogisticRegression(),
                                         n_estimators=50,
                                         random_state=42)

# モデルの訓練
generalized_bagging.fit(X_train, y_train)

# テストデータで予測
y_pred = model.predict(X_test)

# 平均二乗誤差の算出
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}") 

ニューラルネットワークの場合：

from sklearn.ensemble import BaggingClassifier
from sklearn.neural_network import MLPClassifier  
from sklearn.model_selection import train_test_split


# バギングの設定
generalized_bagging = BaggingClassifier(estimator=MLPClassifier(),  
                                         n_estimators=50,
                                         random_state=42)

# モデルの訓練
generalized_bagging.fit(X_train, y_train)

# テストデータで予測
y_pred = model.predict(X_test)

# 平均二乗誤差の算出
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}") 

ブースティング (Boosting)

ブースティングは、弱い学習器（例えば、単純な決定木）を順次訓練し、各モデルが前のモデルの誤差を補正する方法です。このアプローチは、各モデルの予測を組み合わせて強力な予測を行います。モデルのバイアスを減少させ、過学習のリスクを軽減する。

$$\hat{y} = \sum_{m=1}^{M} \alpha_m h_m(x)$$

$\hat{y}​$ は最終的な予測値。$M$ は訓練したモデルの数。$h_m(x)$ は第 $m$ 番目のモデルによる予測。

$α_m​$ は第 $m$ 番目のモデルの重み（通常、誤差に基づいて調整される）

Gradient Boosting：

通常のブースティングです。残差を学習することにより予測精度を向上させる効果的な手法です。多くの実用的な機械学習タスクで高いパフォーマンスを示し、XGBoostやLightGBMのような進化版が存在しますが、基礎的な勾配ブースティングの理解は非常に重要です。

特徴	説明
予測精度の向上	複数の弱い学習器を組み合わせることで、単一のモデルよりも予測精度が向上する傾向があります。
過学習の抑制	各モデルが前のモデルの残差を学習するため、特定の訓練データに過度に適合するのを防ぎます。
頑健性の向上	弱い学習器がノイズに対して敏感な場合でも、複数のモデルを組み合わせることでノイズの影響を軽減できます。

# 必要なライブラリのインポート
from sklearn.ensemble import GradientBoostingClassifier

# Gradient Boostingの設定
gb_model = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)

# モデルの訓練
gb_model.fit(X_train, y_train)

# テストデータでの予測
y_pred = gb_model.predict(X_test)

# 精度の評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

様々なブースティング手法

ブースティング手法	説明
XGBoost	勾配ブースティングを強化したライブラリで、計算速度と性能が向上しています。多くのハイパーパラメータの調整が可能で、正則化機能も備えています。
LightGBM	Microsoftが開発した勾配ブースティングライブラリで、ヒストグラムベースのアルゴリズムを使用し、高速かつ大規模データセットに適しています。
AdaBoost (Adaptive Boosting)	最初に弱い学習器（例：決定木）を訓練し、誤分類されたサンプルに重点を置いて次の学習器を訓練します。複数の弱いモデルを組み合わせて強力なモデルを作成します。
Gradient Boosting Machine (GBM)	通常の勾配ブースティング手法で、各決定木は前のモデルの残差を学習します。XGBoostやLightGBMはこのアプローチを拡張したものです。
CatBoost	Yandexによって開発されたブースティングライブラリで、カテゴリ変数を直接処理する能力があります。データの前処理が少なくて済み、モデルの汎化性能が高いです。
HistGradientBoosting	Scikit-learnに実装された勾配ブースティング手法で、ヒストグラムを利用して計算を高速化します。特に大規模なデータセットに対して効率的です。
Stochastic Gradient Boosting	各ブースティングステップでランダムにサンプルを選択してモデルを訓練する手法です。過学習を防ぎ、モデルの汎化性能を向上させることができます。
Regularized Boosting	追加の正則化項を導入することで、過学習を防ぐための拡張された勾配ブースティング手法です。XGBoostやLightGBMにもこの機能が含まれています。

XGBoost

勾配ブースティングを強化したライブラリで、計算速度と性能が向上しています。多くのハイパーパラメータ調整と正則化機能を備えています。

pip install xgboost

import xgboost as xgb

# XGBoostモデルの作成
model = xgb.XGBClassifier(n_estimators=100, max_depth=5)
model.fit(X_train, y_train)

# テストデータでの予測
y_pred = gb_model.predict(X_test)

# 精度の評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

LightGBM

ヒストグラムベースのアルゴリズムを採用しており、高速な学習と効率的なメモリ使用が特徴です。また、特に大規模データセットに適しており、複数のハイパーパラメータ調整が可能で、正則化機能も備えています。

import lightgbm as lgb

# LightGBMモデルの作成
model = lgb.LGBMClassifier(n_estimators=100, max_depth=5)
model.fit(X_train, y_train)

# テストデータでの予測
y_pred = gb_model.predict(X_test)

# 精度の評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

LightGBMは、分類問題と回帰問題の両方で使用できる、高速で高精度な機械学習アルゴリズムです。特に、大規模データセットや高次元データの分析、構造化データの予測タスクに適しています。

AdaBoost

最初に弱い学習器（例：決定木）を訓練し、誤分類されたサンプルに重点を置いて次の学習器を訓練します。これを繰り返し、複数の弱いモデルを組み合わせて強力なモデルを作成します。

# 必要なライブラリのインポート
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier

# AdaBoostの設定
ada_model = AdaBoostClassifier(estimator=DecisionTreeClassifier(max_depth=1),  # 弱学習器としての決定木
                               n_estimators=50,  # 学習器の数
                               random_state=42)

# モデルの訓練
ada_model.fit(X_train, y_train)

# テストデータでの予測
y_pred = ada_model.predict(X_test)

# 精度の評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

バギングとブースティングの違い

どちらの手法も過学習を抑える弱学習器を基にしたアンサンブル学習です。

• バギング：モデルのバリアンスを減少させることで過学習を防ぐ。
• ブースティング：モデルのバイアスを減少させ、過学習のリスクを軽減する。

特徴	バギング (Bagging)	ブースティング (Boosting)
モデルの訓練方法	複数のモデルを独立に訓練し、それらの予測を平均化または多数決で集約する。	複数のモデルを順次訓練し、前のモデルの残差を学習する。
データのサンプリング	異なるサブセットをリプレイスメントでサンプリングし、各モデルを訓練。	各モデルは前のモデルの誤りに重点を置いて訓練され、重みが調整される。
モデルの重み付け	各モデルは同じ重みを持つ。	後のモデルは前のモデルの誤分類されたサンプルに対して重みを増やす。
過学習の抑制	モデルのバリアンスを減少させることで過学習を防ぐ。	モデルのバイアスを減少させ、過学習のリスクを軽減する。
予測精度の向上	主にモデルのバリアンスを減少させるため、精度が向上する傾向がある。	各モデルが前のモデルの誤りを改善するため、全体の予測精度が向上する。
モデルの依存関係	モデル同士は独立している。	モデル同士は順次依存している。

学習の狙い

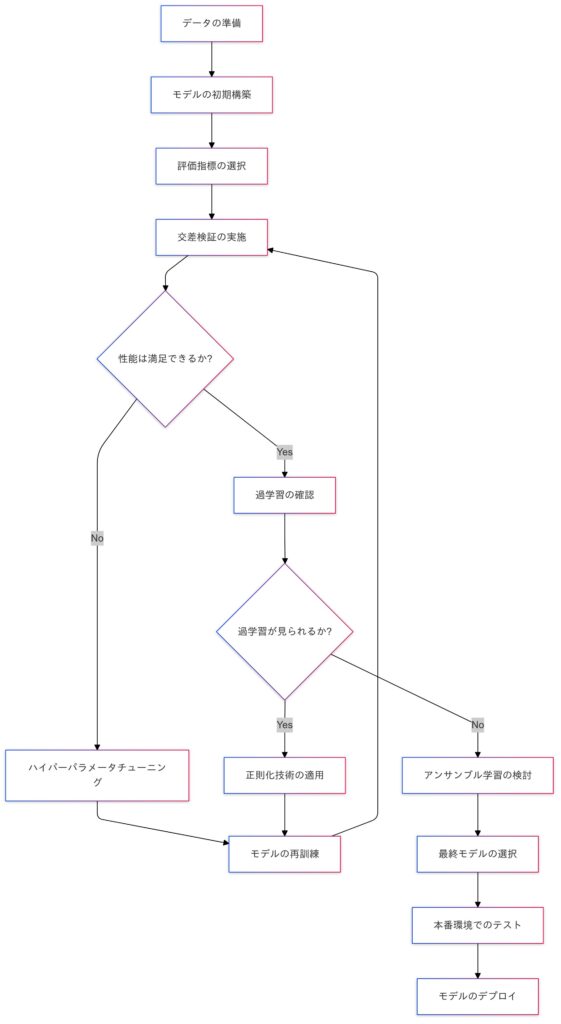
モデルの評価と最適化は、機械学習プロジェクトにおいて不可欠なステップです。適切な評価指標を選択し、交差検証でモデルの汎化性能を確認し、ハイパーパラメータチューニングや過学習の防止策を講じることで、モデルの性能を最大限に引き出すことができます。さらに、アンサンブル学習を活用することで、単一のモデルでは得られない高い予測性能を実現できます。

流れ	説明
データの準備	モデル訓練に必要なデータを収集し、前処理を行う。
モデルの初期構築	モデルの初期構造を設計し、基本的なハイパーパラメータを設定する。
評価指標の選択	モデルの性能を測定するための適切な評価指標を選択する。
交差検証の実施	訓練データを使用してモデルの汎化性能を確認するために交差検証を行う。
性能は満足できるか？	モデルの性能が基準を満たしているかを評価し、次のステップへ進むか決定する。
はい	過学習の確認を行い、モデルが適切に学習できているかを評価する。
いいえ	ハイパーパラメータチューニングを行い、モデルの改善を図る。
過学習が見られるか？	モデルが過学習しているかを確認し、対処方法を検討する。
はい	正則化技術を適用し、モデルの再訓練を行う。
いいえ	アンサンブル学習の検討を行い、さらに性能を向上させる手段を探る。
最終モデルの選択	最も性能の良いモデルを選択し、最終的なデプロイ準備を行う。
本番環境でのテスト	選択したモデルを本番環境でテストし、実際のデータに対する性能を評価する。
モデルのデプロイ	実際の運用環境にモデルを導入し、ユーザーや他のシステムが利用できるようにする。

補足：モデル評価時のテストデータへの前処理の判断基準

この表では、モデル評価の目的とテストデータの性質に応じた前処理の推奨を示しています。

評価目的	テストデータの性質	前処理の有無	理由
汎化性能の評価	テストデータが現実世界のデータを表している	前処理を施さない	現実世界のデータ分布に沿ったモデル性能を確認するため。データの自然な分布を変えずに評価することで、未知データへの適用性を確認しやすい。
汎化性能の評価	テストデータが学習データと同じ分布を持たない（分布が異なる）	前処理を施さない	実運用環境と近い評価が求められる場合、データの加工を避けて分布のズレを考慮した評価が重要になるため。
特定データに対する性能評価	テストデータが学習データと同じ分布を持つ	学習データと同じ標準化を施す	学習データに基づいたスケールに合わせることで、訓練と同じ基準でモデル性能を確認可能になるため。
汎化性能の評価または性能確認	テストデータが新しい環境のデータ	一部の前処理のみを施す（例: 欠損値補完）	新しい環境でも汎用的に適用可能な一部の前処理を施し、異常なデータや欠損に対応しつつ評価するため。

実践への応用

• Kaggleでの活用：これらの技術をKaggleのコンペティションで実践し、上位を目指しましょう。
• コードの拡張：提供したコード例をベースに、自分のデータセットで試してみてください。
• 更なる学習：各手法の理論的な背景も深掘りすると、より効果的にモデルを最適化できます。

次回予告

本回では、モデル評価と最適化に関するさまざまな技術を学びました。分類モデルの評価指標である混合行列や精度、適合率、再現率、F1スコア、AUC-ROC曲線について深く理解することで、モデルの性能を正確に評価する方法を習得しました。さらに、回帰モデルにおける評価指標として平均二乗誤差（MSE）や平均絶対誤差（MAE）についても考察し、それぞれの指標が有効なケースについて学びました。

過学習と汎化性能の重要性を理解し、交差検証やホールドアウト法などの手法を用いることで、モデルの性能をより正確に評価できるようにもなりました。これらの知識を基に、次回は「線形回帰とロジスティック回帰の実装」に進みますが、ここで重要な役割を果たすのが最急降下法です。この手法を通じて、モデルのパラメータを最適化し、より良い予測を行う方法を学びます。

次回の内容にご期待ください。

◾️参考資料

scikit-learn: machine learning in Python — scikit-learn 1.5.2 documentation

scikit-learn.org

Kaggle: Your Machine Learning and Data Science Community

Kaggle is the world’s largest data science community with powerful tools and resources to help you achieve your data sci...

www.kaggle.com