【第5回】モデル評価と最適化（前編）

目的

このブログシリーズでは、機械学習の基礎から応用までを体系的に学び、Kaggleコンペティションに出場し、メダルを獲得するためのスキルを身につけることを目指します。単なる知識の吸収にとどまらず、学んだ理論やアルゴリズムを実際の競技に応用できる力を養うことが目的です。この過程で、実践的な演習やプロジェクトを通じて、手を動かしながら学ぶ姿勢を大切にしていきます。

第5回の目標

第5回の目標は、機械学習モデルの評価と最適化に関する技術を深く理解し、実践的なスキルを身につけることです。具体的には、モデルの性能を正確に評価するための各種モデルの指標（精度、適合率、再現率、F1スコア、AUC-ROC曲線、平均二乗誤差）の定義や適用例を学ぶことで、評価基準の重要性を理解します。また、交差検証の技術を習得し、K分割交差検証やLeave-One-Out交差検証を通じてモデルの汎化性能を評価し、過学習を防ぐ方法をマスターします。さらに、ハイパーパラメータの最適化手法であるグリッドサーチ、ランダムサーチ、ベイズ最適化を実践することで、モデル性能の最大化に向けた能力を養います。過学習を防ぐための正則化やドロップアウトなどの技術についても理解を深め、アンサンブル学習を通じて複数のモデルを組み合わせる方法を学ぶことで、高い予測性能を実現します。これにより、Kaggleコンペティションにおいて競争力のあるモデルを構築し、実践的なデータ解析スキルを向上させることを目指します。

分類モデルの評価指標（混合行列）

機械学習モデルの性能を正確に評価するためには、適切な評価指標を選択することが重要です。

分類の評価指標は、モデルの予測結果を数値化し、正しくクラスを判別する能力を測定するための基準です。これらの指標は、モデルが異なるクラスをどれだけ正確に識別できるかを評価するものであり、クラスの分布や不均衡性に応じて適切な指標を理解し、活用することが求められます。選択した評価指標により、モデルの改善点や実際の応用における性能を明確に把握することが可能になります。

精度 (Accuracy)

精度は、全サンプルのうち、正しく予測されたサンプルの割合を示します。計算式は次の通りです。

$$\text{精度(Accuracy)} = \frac{\text{全サンプル数}}{\text{正しく予測されたサンプル数}}
$$
​

適用例：

精度は、クラスが均等に分布している分類問題で有効です。たとえば、クラスAとクラスBがほぼ同数存在する場合、精度はモデルのパフォーマンスを適切に示します。

注意点：

クラス不均衡なデータでは、精度だけではモデルの性能を正確に評価できない場合があります。例えば、99%がクラスAで1%がクラスBのデータセットでは、すべてをクラスAと予測しても高い精度が得られてしまいます。

Pythonでの実装例

第3回の復習も含め、タイタニック号のデータを使って評価指標の精度の説明を行います。

【第3回】データの前処理と可視化のブログから欠損値の補完、カテゴリカル変数のエンコーディング、データの分割、特徴量のスケーリング、外れ値の検出を使ってモデル学習を行うためにデータの前処理を行います。

ブログではscikitlearnは使わずに説明しましたが、今回のブログではscikitlearnを使って説明します。

まずはcsvデータのダウンロードを行い、scikitlearnのインポートを行います。前処理のコーディングを見ながらどのライブラリを使っているのかを照らし合わせてみてください。

from sklearn.model_selection import train_test_split 
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import LocalOutlierFactor
import pandas as pd

次にデータを読み込み、そのデータの前処理を行います。

# データの読み込み
df = pd.read_csv('titanic.csv') 

# 欠損値の補完
imputer = SimpleImputer(strategy='mean')  # 平均値で補完
numerical_cols = ['Age', 'Fare']
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数のエンコーディング
df['Sex'] = df['Sex'].map({'male': 0, 'female': 1})
df['Embarked'] = df['Embarked'].fillna('S')  # 最頻値で補完
df = pd.get_dummies(df, columns=['Embarked'], prefix='Embarked')

# 特徴量と目的変数の分離
X = df[['Pclass', 'Sex', 'Age', 'Fare', 'SibSp', 'Parch', 'Embarked_C', 'Embarked_Q', 'Embarked_S']]
y = df['Survived']

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# スケーリング
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 外れ値の検出と処理
lof = LocalOutlierFactor(n_neighbors=20, contamination=0.05)
outlier_pred = lof.fit_predict(X_train)
X_train = X_train[outlier_pred == 1]
y_train = y_train[outlier_pred == 1]

今回のブログではモデル学習のことまでは触れませんが、評価指標を適合するためにはモデル学習が必要になってきますので、モデル学習を行うために今回は機械学習アルゴリズムであるランダムフォレストを使ってモデル学習を行います。

# モデルの学習
model = RandomForestClassifier(random_state=42) # ランダムフォレスト
model.fit(X_train, y_train)

# テストデータに対する予測
y_pred = model.predict(X_test)

次に先ほど説明した分類の評価指標である精度 (Accuracy)を使ってモデル学習を行った予測データにテストデータを使って評価をしてみます。

# 評価指標の算出
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

出力：

Accuracy: 0.79

出力された Accuracy: 0.79 は、タイタニック号の生存予測モデルがテストデータに対してどれくらい正確に予測できたかを示す指標です。この場合、Accuracy が 0.79 とは、テストデータの約 79% について、モデルが生存状況を正しく予測できたことを意味します。

しかし、データセットのクラスのバランスが偏っている場合、Accuracy は必ずしもモデルの性能を正確に反映しない場合があります。

適合率 (Precision) と再現率 (Recall)

適合率（Precision）と再現率（Recall）は、特に不均衡なデータセットにおいてモデルの性能を評価する際に重要な指標です。

	実際は正	実際は負
正と予測	真陽性 (TP)	偽陽性（FP）
負と予測	偽陰性（FN）	真陰性（TN）

適合率 (Precision)

適合率は、モデルが正と予測したサンプルのうち、実際に正であるサンプルの割合を示します。つまり、モデルの正の予測がどれだけ信頼できるかを測定します。

$$\text{適合率 (Precision)} = \frac{\text{真陽性 (TP)}}{\text{真陽性 (TP) + 偽陽性（FP）}}
$$

​適用例：

適合率は、スパムフィルタリングなどのアプリケーションで特に重要です。偽陽性が多いと、正当なメールがスパムとして誤って分類されるリスクがあります。

再現率 (Recall)

再現率は、実際に正であるサンプルのうち、モデルが正しく予測した割合を示します。つまり、モデルがどれだけ多くの実際の正のサンプルを捉えられるかを測定します。

$$\text{再現率 (Recall)} = \frac{\text{真陽性 (TP)}}{\text{真陽性 (TP) + 偽陰性（FN）}}
$$

適用例：

再現率は、病気の診断などで特に重要です。偽陰性が多いと、病気があるのに検出できないリスクがあります。

適合率（Precision）と再現率（Recall）は、特に不均衡なデータセットにおいてモデルの性能を評価する際に重要な指標です。以下では、これらの指標を詳しく説明し、さらに精度、適合率、再現率、F1スコアの関係を示す表を生成します。

from sklearn.metrics import precision_score, recall_score

precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
print(f"Precision: {precision:.2f}")
print(f"Recall: {recall:.2f}")

出力：

PrecisionとRecallが共に0.73～0.75と、比較的高い値を示していることから、モデルは生存者と非生存者の両方のクラスに対して、ある程度の予測精度を達成していると考えられます。

Precision: 0.75
Recall: 0.73

データセットのクラスのバランスが偏っている場合は、Accuracyだけでなく、PrecisionやRecallなどの指標も合わせて確認する必要があります。これらの指標を総合的に判断することで、モデルの性能をより正確に評価することができます

PrecisionとRecall：

Precision（適合率）は、予測結果がPositive(正)と判定されたデータのうち、実際にPositive
(正）であったデータの割合を示します。

Recall（再現率）は、実際にPositive(正)であったデータのうち、正しくPositive(正)と予測できたデータの割合を示します。

F1スコア

F1スコアは、適合率（Precision）と再現率（Recall）の調和平均を示す指標であり、特に不均衡なデータセットにおいてモデルの性能を評価する際に非常に重要です。F1スコアは、両者のバランスを考慮し、いずれか一方が低いと全体のスコアが低くなるため、モデルが真のポジティブを見逃さず、同時に誤ったポジティブを減らすことを目指します。

$$\frac{2 \times \text{適合率(Precision)} \times \text{再現率(Recall)}}{\text{適合率(Precision)} + \text{再現率(Recall)}}$$

この式からわかるように、F1スコアは適合率と再現率がともに高い場合に高い値を取り、どちらか一方が低いとスコアも低くなります。

適用例

クラス不均衡が存在する場合：

たとえば、スパムメール検出や病気診断など、ポジティブクラスが少ない状況で、適合率と再現率の両方を評価したい場合。

ビジネス上の意思決定において重要性が高い場合：

偽陽性が多いと顧客を失ったり、偽陰性が多いと機会損失を招いたりするため、両者をバランスよく評価する必要があります。

from sklearn.metrics import f1_score

# y_test: 正解ラベル, y_pred: 予測ラベル
f1 = f1_score(y_test, y_pred)
print(f"F1 Score: {f1:.2f}")

出力：

F1 Score: 0.74

F1スコアは、PrecisionとRecallのバランスを考慮した指標であり、特にクラスのバランスが偏っている場合に有効です。0.74というF1スコアは、そこそこの性能を示唆していますが、PrecisionとRecallの値も合わせて確認することが重要です。

精度、適合率、再現率、F1スコアの関係

これらの指標の関係を理解するために、次の表を生成します。以下のテーブルには、各指標の定義と簡単な説明が含まれています。

指標名	定義	説明
精度 (Accuracy)	$(\frac{\text{正しく予測されたサンプル数}}{\text{全サンプル数}})$	全体の予測がどれだけ正確かを示すが、不均衡データには注意が必要。
適合率 (Precision)	$(\frac{\text{真陽性 (TP)}}{\text{真陽性 (TP)} + \text{偽陽性 (FP)}})$	正と予測されたサンプルの中で、実際に正である割合。
再現率 (Recall)	$(\frac{\text{真陽性 (TP)}}{\text{真陽性 (TP)} + \text{偽陰性 (FN)}})$	実際に正であるサンプルの中で、正しく予測された割合。
F1スコア	$(\frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}})$	適合率と再現率の調和平均で、バランスを評価する指標。

AUC-ROC曲線

ROC曲線の定義

ROC（Receiver Operating Characteristic）曲線は、機械学習モデルの性能を視覚的に評価するための手法です。この曲線は、異なる閾値でのモデルの真陽性率（TPR）と偽陽性率（FPR）の関係を示します。

真陽性率 (TPR)：

実際にポジティブなサンプルのうち、モデルが正しくポジティブと予測した割合です。これは再現率とも呼ばれます。

$$\text{TPR (真陽性率)} = \frac{\text{真陽性 (TP)}}{\text{真陽性 (TP) + 偽陰性（FN）}}
$$

偽陽性率 (FPR)：

実際にはネガティブなサンプルのうち、モデルが誤ってポジティブと予測した割合です。

$$\text{FPR (偽陽性率)} = \frac{\text{偽陽性 (FP)}}{\text{偽陽性 (FP) + 真陰性（TN）}}
$$

ROC曲線は、FPRを横軸、TPRを縦軸にプロットすることで得られます。異なる閾値に基づくモデルのパフォーマンスを視覚的に比較することができ、どの閾値が最適かを見極める助けになります。

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score, roc_curve
import matplotlib.pyplot as plt

# 予測確率を取得
# タイタニックデータの場合、目的変数「生存」を予測する際に、クラス1は「生存」を表すので、y_scores[:, 1]でクラス1の確率を取得するのが適切です。
y_scores = model.predict_proba(X_test)[:, 1]  # クラス1の確率

auc = roc_auc_score(y_test, y_scores)
print(f"AUC: {auc:.2f}")

出力：

AUC: 0.89

AUCが0.89という値は、タイタニックの生存予測モデルにおいて、非常に良い分類性能を示しています。このモデルは、生存者と非生存者を高い精度で区別できていると考えられます。

AUC (Area Under the Curve)とは？

AUCは、ROC曲線の下の面積を示します。この値は、モデルの全体的な性能を数値化するものであり、以下のように解釈されます。

AUC = 1：

完璧なモデルを示します。すべてのポジティブサンプルを正しく予測し、すべてのネガティブサンプルを誤って予測しないモデルです。

AUC = 0.5：

ランダムな予測を示します。この場合、モデルはポジティブとネガティブのサンプルを区別できていないことになります。

AUC < 0.5：

モデルが逆の予測をしていることを示します。これは非常に良くない結果です。

ROC曲線との関係

閾値(threshold)、FPR、TPRの組み合わせは、ROC曲線を描くためのデータポイントになります。ROC曲線は、様々な閾値におけるFPRとTPRの関係をグラフで表したものです。

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score, roc_curve
import matplotlib.pyplot as plt

# 予測確率を取得
# タイタニックデータの場合、目的変数「生存」を予測する際に、クラス1は「生存」を表すので、y_scores[:, 1]でクラス1の確率を取得するのが適切です。
y_scores = model.predict_proba(X_test)[:, 1]  # クラス1の確率

auc = roc_auc_score(y_test, y_scores)
fpr, tpr, thresholds = roc_curve(y_test, y_scores)

print(f"AUC: {auc:.2f}")

# 閾値と対応するTPR, FPRを表示（一部のみ）
for i in range(0, len(thresholds), 10):  # 例：10個に1つ表示
    threshold = thresholds[i]
    fpr_val = fpr[i]
    tpr_val = tpr[i]
    print(f"Threshold: {threshold:.2f}, FPR: {fpr_val:.2f}, TPR: {tpr_val:.2f}") 
plt.plot(fpr, tpr, label=f"AUC = {auc:.2f}")
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend()
plt.show()

出力：

出力結果を見ると、閾値が大きくなるにつれて、FPRは小さくなり、TPRも小さくなっていることがわかります。これは、閾値を高く設定すると、陽性と判定されるデータが減り、誤って陽性と判定される確率（FPR）も減る一方で、正しく陽性と判定される確率（TPR）も減ることを意味しています。

AUC: 0.89
Threshold: 0.89, FPR: 0.04, TPR: 0.47
Threshold: 0.64, FPR: 0.09, TPR: 0.72
Threshold: 0.39, FPR: 0.21, TPR: 0.78
Threshold: 0.22, FPR: 0.31, TPR: 0.88
Threshold: 0.13, FPR: 0.44, TPR: 0.93
Threshold: 0.05, FPR: 0.59, TPR: 0.99

例）閾値0.64の場合

閾値が0.64のとき、FPRは0.09、TPRは0.72です。

これは、実際に陰性であるデータの約9%が陽性と誤って判定され、実際に陽性であるデータの約72%が陽性と正しく判定されることを意味します。

閾値（Threshold)：

分類モデルが「陽性」と判定する確率の基準です。例えば、閾値が0.5の場合、予測確率が0.5以上であれば「陽性」、0.5未満であれば「陰性」と判定されます。

偽陽性率（FPR)：実際に陰性であるデータが、陽性と誤って判定される確率です。

真陽性率（TPR)：実際に陽性であるデータが、陽性と正しく判定される確率です。

ビジネスにおける活用

• 誤って陽性と判定されるリスクを低く抑えたい場合は、FPRが低い閾値を選択します。
• 実際に陽性であるデータをできるだけ多く見逃したくない場合は、TPRが高い閾値を選択します。

この情報を利用することで、ビジネスの目的に最適な閾値を選択し、モデルをより効果的に活用することができます。

それぞれの評価指標が有効なケース（分類モデル）

指標名	定義	有効なケース	例
Accuracy (精度)	正しく分類できたデータの割合。	全てのクラスの誤分類コストが同じで、データの偏りが少ない場合。	顧客満足度調査の結果を分類する場合。
Precision (適合率)	陽性と予測したデータのうち、実際に陽性だったデータの割合。	陽性と誤って予測してしまうことのリスクが高い場合。	スパムメール検知（スパムと誤って判定してしまうことを避けたい）。
Recall (再現率)	実際に陽性だったデータのうち、陽性と正しく予測できたデータの割合。	陽性を誤って陰性と予測してしまうことのリスクが高い場合。	癌の診断（癌を見逃してしまうことを避けたい）。
F1-score (F1スコア)	PrecisionとRecallの調和平均。	PrecisionとRecallのバランスを重視する場合。	顧客ターゲティング（PrecisionとRecallのどちらかを犠牲にしたくない場合）。
ROC AUC	ROC曲線の下側の面積。ROC曲線は、真陽性率（TPR）と偽陽性率（FPR）の関係を示す。	閾値を変更した場合のモデルの性能を評価したい場合、またはクラスのバランスが大きく異なる場合。	PrecisionとRecallのバランスを調整したい場合。

回帰モデルの評価指標

回帰モデルの性能を正しく評価するためには、適切な評価指標を選ぶことが非常に重要です。回帰の評価指標は、モデルが予測した数値と実際の値との誤差を測定し、どれだけ正確に予測できているかを示します。これらの指標は、予測が実際の値にどれだけ近いかを評価することに焦点を当てています。評価指標の選び方は、データの特性や問題の内容によって異なるため、どの指標を使うべきかを理解することが大切です。適切な評価指標を使用することで、モデルの弱点を見つけやすくなり、より良い予測を目指す手助けになります。

平均二乗誤差 (MSE)

平均二乗誤差（Mean Squared Error, MSE）は、モデルの予測値と実際の値との間の誤差を評価するための指標です。具体的には、各予測値と実際の値の差を二乗し、その平均を取ることで計算されます。MSEの計算式は以下のように表されます。

$$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2$$

ここで、$y_i$ は実際の値、$\hat{y}_i$ は予測値、$n$ はデータの数です。

• MSE（平均二乗誤差）は常に非負の値を取ります。
• MSEの値が小さいほど、モデルの予測が実際の値に近いことを示します。
• 値が小さなMSEは、より正確な予測ができているということを意味します。

適用例：

• 住宅価格の予測
• 気温の予測

Pythonでの実装例

回帰の際もタイタニック号のデータを使って説明するのですが、回帰の場合は分類のアルゴリズムであるランダムフォレストではなく回帰のアルゴリズムである線形回帰のアルゴリズムを使います。

まずはライブラリをインポートしてデータを読み込み、データの前処理を行います。

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression  # 線形回帰のライブラリ
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import LocalOutlierFactor
import pandas as pd

# データの読み込み
df = pd.read_csv('titanic.csv') 

# 欠損値の補完
imputer = SimpleImputer(strategy='mean')  # 平均値で補完
numerical_cols = ['Age', 'Fare']
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数のエンコーディング
df['Sex'] = df['Sex'].map({'male': 0, 'female': 1})
df['Embarked'] = df['Embarked'].fillna('S')  # 最頻値で補完
df = pd.get_dummies(df, columns=['Embarked'], prefix='Embarked')

# 特徴量と目的変数の分離
X = df[['Pclass', 'Sex', 'Age', 'Fare', 'SibSp', 'Parch', 'Embarked_C', 'Embarked_Q', 'Embarked_S']]
y = df['Survived']

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# スケーリング
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 外れ値の検出と処理
lof = LocalOutlierFactor(n_neighbors=20, contamination=0.05)
outlier_pred = lof.fit_predict(X_train)
X_train = X_train[outlier_pred == 1]
y_train = y_train[outlier_pred == 1]

# モデルの学習
model = LinearRegression()  # 回帰モデルに変更
model.fit(X_train, y_train)

# テストデータに対する予測
y_pred = model.predict(X_test)

次に先ほど説明した回帰の評価指標である平均二乗誤差 (MSE)を使ってモデル学習を行った予測データにテストデータを使って評価をしてみます。

from sklearn.metrics import mean_squared_error

# y_test: 実際の値, y_pred: モデルの予測値
mse = mean_squared_error(y_test, y_pred)
print(f"MSE: {mse:.2f}")

出力：

MSE: 0.13

生存確率予測の場合の解釈：

生存確率を予測するモデルでMSEが0.13であれば、平均的に予測値と実際の値の差が約0.36（√0.13）程度であることを意味します。これは、生存確率を0から1の範囲で予測している場合、平均的に約0.36の誤差があることを示しています。

もし、0.36の誤差が大きすぎると判断される場合は、以下の改善策を検討することができます。

特徴量の追加

• モデルに新しい特徴量を追加することで、予測精度を向上させることができます。例えば、乗客の年齢、性別、乗船クラス、運賃などの他に、客室の場所、家族構成、チケットの種類などの特徴量を追加することができます。

モデルの変更

• 線形回帰以外のモデル（例えば、ランダムフォレスト、勾配ブースティングなど）を試すことで、予測精度を向上させることができます。

ハイパーパラメータのチューニング

• モデルのハイパーパラメータを調整することで、予測精度を向上させることができます。例えば、ランダムフォレストの場合、木の数、深さ、分割基準などを調整することができます。

データの前処理の改善

• 欠損値の処理方法、外れ値の処理方法、特徴量のスケーリング方法などを変更することで、予測精度を向上させることができます。

平均絶対誤差 (MAE)

平均絶対誤差（MAE）は、モデルの予測と実際の観測値の間の誤差の大きさを評価するための指標です。外れ値に敏感でなく、異常値が多い場合でも有用で、汎用性に優れた指標です。

$$\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i – \hat{y}_i|$$

適用例：

• 気温の予測
• 外れ値が少ない場合

MAEが小さいほど、モデルの予測精度が高いことを示します。

from sklearn.metrics import mean_absolute_error

# y_test: 実際の値, y_pred: モデルの予測値
mae = mean_absolute_error(y_test, y_pred)
print(f"MAE: {mae:.2f}")

出力：

MAE: 0.28

MAEが0.28ということは、予測値と実際の値の差が平均的に0.28であることを示しています。これは、生存確率を0から1の範囲で予測している場合、平均的に約0.28の誤差があることを意味します。MAEの値を解釈する際には、目的変数の単位に注意する必要があります。

決定係数 (R²)

決定係数（R-squared）は、モデルがデータのばらつきをどれだけ説明できるかを示す指標です。値は0から1の間で、1に近いほどモデルの適合度が良いことを示します。

$$R^2 = 1 – \frac{\sum_{i=1}^{n} (y_i – \hat{y})^2}{\sum_{i=1}^{n} (y_i – \bar{y}_i)^2}$$

適用例：

• 病気のリスク予測
• 消費支出の分析
• 広告効果の評価

注意点：

• R²は、回帰分析においてモデルの説明力を評価するために広く用いられます。ただし、MSEやMAEと異なり、R²はモデルの複雑さを考慮しないため、過学習の可能性を持つことに注意が必要です
• R²は主に線形回帰モデルに適用されるため、非線形モデルでは解釈が難しくなることがあります。
• R²は外れ値に敏感であり、外れ値が存在する場合には不適切な評価をすることがあります。
• R2乗は、モデルの複雑さに影響を受けます。モデルが複雑になるほど、R2乗は大きくなりやすくなります。

from sklearn.metrics import r2_score

# y_test 実際の値, y_pred: モデルの予測値
r2 = r2_score(y_test, y_pred)
print(f"R-squared (R²): {r2:.2f}")

出力：

R-squared (R²): 0.45

タイタニックの生存予測の回帰モデルにおいて、R2乗が0.45ということは、モデルがデータのばらつきの45%を説明できていることを意味します。R2乗が0.45ということは、モデルがデータのばらつきをある程度説明できていますが、まだ改善の余地があることを示唆しています。

ルート平均二乗誤差 (RMSE)

RMSEもMSE同様、モデルの予測値と実際の値との誤差を評価する指標です。

元のデータと同じ単位で表現されるため、誤差の解釈が容易であり、モデルの改良に向けた具体的な目標として設定できます。ただし、外れ値の影響やモデルの複雑さを考慮しない限界があるため、他の評価指標と組み合わせて使用することが望ましいです。

$$\text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i – \hat{y}_i)^2}$$

適用例：

• 気象予測
• 販売予測
• 医療データ分析

RMSEが小さいほど、予測値と実際の値の差が小さく、モデルの予測精度が高いことを示します。

注意点：

• R2乗と同様に、モデルの複雑さに影響を受けます。 モデルが複雑になるほど、RMSEは小さくなりやすくなります。
• 必ずしもモデルの予測精度が高いことを意味するわけではありません。 例えば、モデルが複雑すぎて過学習を起こしている場合、RMSEは小さくなる可能性がありますが、予測精度が低い可能性があります。
• 外れ値の影響を受けやすいという特徴があります。

from sklearn.metrics import mean_squared_error
import numpy as np

# y_test: 実際の値, y_pred: モデルの予測値
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
print(f"RMSE: {rmse:.2f}")

出力：

RMSE: 0.37

RMSEが0.37ということは、予測値と実際の値の差が平均的に0.37であることを示しています。これは、生存確率を0から1の範囲で予測している場合、平均的に約0.37の誤差があることを意味します。RMSEの値を解釈する際には、モデルの複雑さ、他の評価指標、および外れ値の影響などを考慮する必要があります。

ルート平均対数誤差（RMSLE）

RMSLEは、予測値と実際の値の対数を取った後の誤差を評価する指標であり、対数を使用することで誤差の相対的な性質を強調し、大きな値の誤差が小さな値に比べて過大評価されるのを防ぎます。RMSLEが小さいほど、モデルの予測精度が高いことを示します。

$$\text{RMSLE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} \left( \log(y_i + 1) – \log(\hat{y}_i + 1) \right)^2}$$

適用例：

• 売上予測
• 人口予測
• 不動産市場分析

RMSLEは、特に売上や人口のように幅広い範囲の数値を扱う場合に有用な評価指標です。対数を使用することで、相対的な誤差を強調し、大きな値と小さな値の誤差を公平に評価します。

注意点：

• RMSLEは、予測値と実際の値が共に正の値である場合にのみ使用できます。
• RMSLEは、対数変換を行うため、外れ値の影響を受けにくいという特徴があります
• RMSLEの値の良し悪しは、問題のドメインやデータセットによって異なります。

import numpy as np

def rmsle(y_test, y_pred):
    """
    ルート平均対数誤差 (RMSLE) を計算する関数
    :param y_test: 実際の値 (numpy array)
    :param y_pred: モデルの予測値 (numpy array)
    :return: RMSLEの値
    """
    # 対数を取るために1を加えた後、平方誤差を計算
    log_test = np.log1p(y_test)
    log_pred = np.log1p(y_pred)
    return np.sqrt(np.mean((log_test - log_pred) ** 2))

# 使用例
y_test = np.array([3, 5, 2.5, 7])
y_pred = np.array([2.5, 5, 4, 6])

rmsle_value = rmsle(y_test, y_pred)
print(f"RMSLE: {rmsle_value:.4f}")

出力：

RMSLE: 0.2018

RMSLEが0.2018と比較的低い値であるため、モデルは予測値と実際の値の比率をある程度正確に予測できていると考えられます。RMSLEの値を解釈する際には、目的変数の単位やデータの分布などを考慮する必要があります。

それぞれの評価指標が有効なケース（回帰モデル）

指標名	定義	有効なケース	例
平均二乗誤差 (MSE)	予測値と実測値の差の二乗の平均。	大きな誤差に対して敏感な場合。	住宅価格の予測など、外れ値が重要な場合。
平均絶対誤差 (MAE)	予測値と実測値の差の絶対値の平均。	外れ値に敏感でない場合や、誤差の解釈が直感的な場合。	気温の予測など、外れ値が少ない場合。
決定係数 (R²)	予測値が実測値をどの程度説明できているかを示す指標。（1に近いほど良いモデル）	モデルの説明力を評価したい場合。	回帰モデルがデータのばらつきをどれだけ説明できるか評価する場合。
RMSE	MSEの平方根。	元のデータと同じ単位で誤差を評価したい場合。	価格予測や収入予測など、直感的な誤差評価が求められる場合。
RMSLE	対数変換した値のRMSE。	予測値が大きく異なる場合や、相対的な変化を評価したい場合。	ユーザー数の予測など、対数変換が有効な場合。

過学習と汎化性能

機械学習において、モデルを訓練データで学習させるだけでは十分ではありません。重要なのは、モデルが見たことのない新しいデータに対しても高いパフォーマンスを発揮できる「汎化性能」を持つことです。

過学習とは？

過学習とは、モデルが訓練データに対して過度に適合してしまい、データのノイズや特異なパターンを学習してしまう現象を指します。これにより、訓練データに対しては高い精度を示しても、未知のデータに対しては正確な予測ができなくなってしまいます。

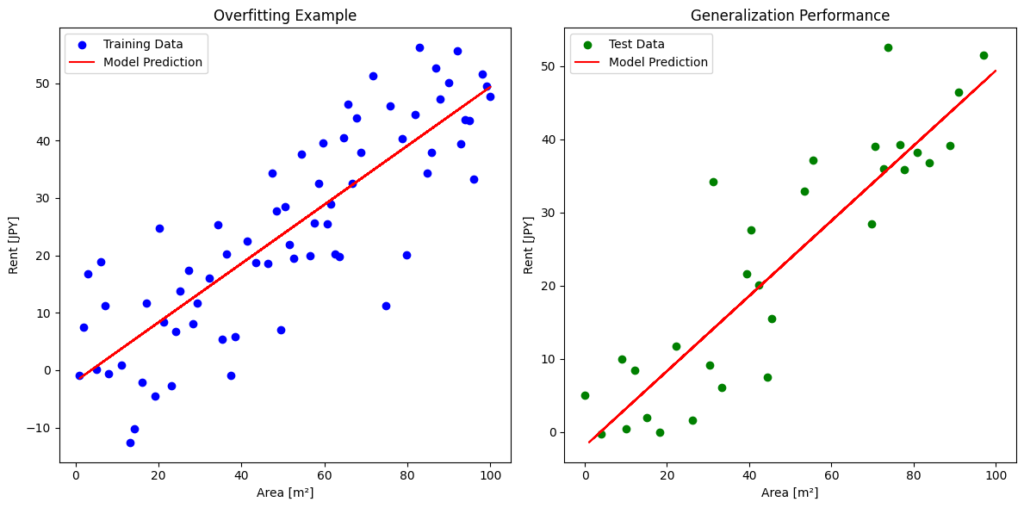
画像に示されたように、左側のグラフは過学習の例です。右側のグラフは適度に学習したモデルを示しており、未知のデータに対しても一定の予測精度を保っています。

過学習の改善策

交差検証の利用：

データを複数のサブセットに分割し、モデルの評価を行うことで、過学習を防ぎ、モデルの汎化性能を向上させる手法。

L1正則化（Lasso）：特徴量の選択を促進し、重要でない特徴量の重みを0にする。

L2正則化（Ridge）：重みの二乗和にペナルティを加えることで、モデルの複雑さを抑制する。

ドロップアウト：

ニューラルネットワークの訓練中にランダムにノードを無効化することで、過学習を防ぎ、モデルのロバスト性を向上させる。

データ拡張：

訓練データを拡張するために、回転、拡大、変形などの技術を使用し、モデルが多様なデータに適応できるようにする。

早期終了（Early Stopping）：

訓練中に検証データの性能が悪化し始めたら、訓練を停止することで、過学習を防ぐ。

アンサンブル学習：

複数のモデルを組み合わせることで、個々のモデルの欠点を補い、全体の予測性能を向上させる。

シンプルなモデルの選択：

モデルの複雑さを抑え、過学習のリスクを減らすために、より単純なアルゴリズムを選ぶ。

バッチ正規化：中間層の出力を正規化することで、学習の安定性を向上させ、過学習を抑える。

交差検証 (Cross-Validation)

交差検証は、機械学習モデルの汎化性能を評価するための重要な手法です。汎化性能とは、モデルが未見のデータに対してどれだけうまく予測できるかを示す指標であり、過学習を防ぐためにも重要です。過学習は、モデルが訓練データに過度に適合し、未知のデータに対する性能が低下する現象です。交差検証を使用することで、モデルの性能をより正確に評価できます。

ホールドアウト法 (Hold-Out Method)

ホールドアウト法は、交差検証の一種であり、モデルの評価を行うためのシンプルで効率的な手法です。この方法では、データセットを訓練データとテストデータに分割します。基本的な流れは以下の通りです。

ホールドアウト法の流れ：

ステップ	説明
データの分割	データセットを訓練データとテストデータに分けます。一般的には、70%〜80%を訓練データ、残りをテストデータとして使用します。
モデルの訓練	訓練データを使用してモデルを訓練します。
性能評価	テストデータを使用してモデルの性能を評価します。このデータはモデルに対して未見のものであるため、汎化性能を示す良い指標となります。

ホールドアウト法の特徴：

特徴	説明
簡便性	ホールドアウト法は実装が簡単で、迅速にモデルの評価ができます。
計算コスト	1回の訓練と評価で済むため、計算リソースを比較的少なく抑えられます。
バイアスの可能性	データの分割によって評価結果がバイアスされる可能性があるため、十分なデータがある場合に注意が必要です。データセットが小さい場合、ランダムに分割することで偏りが生じることがあります。

下のPythonコードを見るとホールドアウト法は先ほどの分類・回帰のどちらの評価指標のコーディングでも使用していたことがわかります。

from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score


# データの読み込み
df = pd.read_csv('titanic.csv') 

# 欠損値の補完
imputer = SimpleImputer(strategy='mean')  # 平均値で補完
numerical_cols = ['Age', 'Fare']
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数のエンコーディング
df['Sex'] = df['Sex'].map({'male': 0, 'female': 1})
df['Embarked'] = df['Embarked'].fillna('S')  # 最頻値で補完
df = pd.get_dummies(df, columns=['Embarked'], prefix='Embarked')

# データセットの準備 (X: 特徴量, y: ラベル)
X = df[['Pclass', 'Sex', 'Age', 'Fare', 'SibSp', 'Parch', 'Embarked_C', 'Embarked_Q', 'Embarked_S']]
y = df['Survived']

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# モデルの訓練
model = RandomForestClassifier()
model.fit(X_train, y_train)

# テストデータでの予測
y_pred = model.predict(X_test)

# モデルの性能評価
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

# データを訓練データとテストデータに分割（この部分がホールドアウト法）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

このコードでは、train_test_split 関数を使って、データセットを80%の訓練データと20%のテストデータに分割しています。そして、訓練データでRandomForestClassifierモデルを学習させ、テストデータで予測を行い、accuracy_score 関数を使って精度を評価しています。

K分割交差検証 (K-fold Cross-Validation)

K分割交差検証は、最も一般的な交差検証の手法です。この手法では、データセットをK個の等しいサイズの部分に分割します。その後、次のようにしてモデルの評価を行います。

ステップ	説明
データの分割	データセットをK個に分割します。たとえば、K=5の場合、データは5つの部分に分けられます。
モデルの訓練と検証	K回の繰り返しを行います。各回で1つの部分を検証データとして使用し、残りのK-1部分を訓練データとして使用します。モデルを訓練し、検証データに対する性能を評価します。
スコアの平均	K回の評価結果を平均して、最終的なモデルの性能を示します。

交差検証法（cross_val_score）を用いた評価指標の算出：

from sklearn.model_selection import KFold, cross_val_score
from sklearn.ensemble import RandomForestClassifier

# データの読み込み
df = pd.read_csv('titanic.csv') 

# 欠損値の補完
imputer = SimpleImputer(strategy='mean')  # 平均値で補完
numerical_cols = ['Age', 'Fare']
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数のエンコーディング
df['Sex'] = df['Sex'].map({'male': 0, 'female': 1})
df['Embarked'] = df['Embarked'].fillna('S')  # 最頻値で補完
df = pd.get_dummies(df, columns=['Embarked'], prefix='Embarked')

# データセットの準備 (X: 特徴量, y: ラベル)
X = df[['Pclass', 'Sex', 'Age', 'Fare', 'SibSp', 'Parch', 'Embarked_C', 'Embarked_Q', 'Embarked_S']]
y = df['Survived']

# K分割交差検証の設定
kf = KFold(n_splits=5, shuffle=True, random_state=42)
model = RandomForestClassifier()

# モデルの交差検証を実行
scores = cross_val_score(model, X, y, cv=kf)
print(f"Cross-Validation Scores: {scores}")
print(f"Mean Score: {scores.mean():.2f}")

交差検証は、モデルの汎化性能を評価するために非常に重要であり、cross_val_score を使うことで簡単に交差検証を実行することができます。

混合行列（精度、適合率、再現率、F1スコア、AUC-ROC曲線）を用いた評価指標の算出：

from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, roc_curve
import matplotlib.pyplot as plt

# データの読み込み
df = pd.read_csv('titanic.csv') 

# 欠損値の補完
imputer = SimpleImputer(strategy='mean')  # 平均値で補完
numerical_cols = ['Age', 'Fare']
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数のエンコーディング
df['Sex'] = df['Sex'].map({'male': 0, 'female': 1})
df['Embarked'] = df['Embarked'].fillna('S')  # 最頻値で補完
df = pd.get_dummies(df, columns=['Embarked'], prefix='Embarked')

# データセットの準備 (X: 特徴量, y: ラベル)
X = df[['Pclass', 'Sex', 'Age', 'Fare', 'SibSp', 'Parch', 'Embarked_C', 'Embarked_Q', 'Embarked_S']]
y = df['Survived']

# K分割交差検証の設定
kf = KFold(n_splits=5, shuffle=True, random_state=42)

# モデルのインスタンスを作成
model = RandomForestClassifier()

# 評価指標を格納するリスト
accuracies = []
precisions = []
recalls = []
f1_scores = []
auc_scores = []
fpr_list = []
tpr_list = []

# K分割交差検証の実行
for train_index, test_index in kf.split(X):
    X_train, X_test = X.iloc[train_index], X.iloc[test_index]
    y_train, y_test = y.iloc[train_index], y.iloc[test_index]

    # モデルの学習
    model.fit(X_train, y_train)

    # テストデータでの予測
    y_pred = model.predict(X_test)
    y_prob = model.predict_proba(X_test)[:, 1]  # 確率値を取得

    # 混合行列の作成
    cm = confusion_matrix(y_test, y_pred)

    # 評価指標の計算
    accuracy = accuracy_score(y_test, y_pred)
    precision = precision_score(y_test, y_pred)
    recall = recall_score(y_test, y_pred)
    f1 = f1_score(y_test, y_pred)
    auc = roc_auc_score(y_test, y_prob)
    fpr, tpr, _ = roc_curve(y_test, y_prob)

    # 評価指標のリストに追加
    accuracies.append(accuracy)
    precisions.append(precision)
    recalls.append(recall)
    f1_scores.append(f1)
    auc_scores.append(auc)
    fpr_list.append(fpr)
    tpr_list.append(tpr)

# 各フォールドの混合行列を表示
for i, cm in enumerate(confusion_matrices):
    print(f"Fold {i+1} Confusion Matrix:")
    print(cm)

# 各フォールドの混合行列を統合して全体的な混合行列を作成
total_cm = sum(confusion_matrices)
print("\nTotal Confusion Matrix:")
print(total_cm) 

# 評価指標の平均値を表示
print(f"\nAverage Accuracy: {np.mean(accuracies):.3f}")
print(f"Average Precision: {np.mean(precisions):.3f}")
print(f"Average Recall: {np.mean(recalls):.3f}")
print(f"Average F1 Score: {np.mean(f1_scores):.3f}")
print(f"Average AUC: {np.mean(auc_scores):.3f}")

# AUC-ROC曲線の描画
plt.figure()
for fpr, tpr in zip(fpr_list, tpr_list):
    plt.plot(fpr, tpr, label='Fold')
plt.plot([0, 1], [0, 1], linestyle='--', color='gray')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('AUC-ROC Curve')
plt.legend()
plt.show() 

少し長くなりましたがこの方法により、K分割交差検証の結果から、精度、適合率、再現率、F1スコア、AUC-ROC曲線を算出することができます。

回帰の評価指標(MSE, RMSE, MAE, R²を用いた評価指標の算出)：

from sklearn.model_selection import KFold
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
import numpy as np

# データの読み込み
df = pd.read_csv('titanic.csv') 

# 欠損値の補完
imputer = SimpleImputer(strategy='mean')  # 平均値で補完
numerical_cols = ['Age', 'Fare']
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数のエンコーディング
df['Sex'] = df['Sex'].map({'male': 0, 'female': 1})
df['Embarked'] = df['Embarked'].fillna('S')  # 最頻値で補完
df = pd.get_dummies(df, columns=['Embarked'], prefix='Embarked')

# データセットの準備 (X: 特徴量, y: ラベル)
X = df[['Pclass', 'Sex', 'Age', 'Fare', 'SibSp', 'Parch', 'Embarked_C', 'Embarked_Q', 'Embarked_S']]
y = df['Survived']

# K分割交差検証の設定
kf = KFold(n_splits=5, shuffle=True, random_state=42)

# モデルのインスタンスを作成
model = LinearRegression()

# 評価指標を格納するリスト
mse_scores = []
rmse_scores = []
mae_scores = []
r2_scores = []

# K分割交差検証の実行
for train_index, test_index in kf.split(X):
    X_train, X_test = X.iloc[train_index], X.iloc[test_index]  # iloc を使用
    y_train, y_test = y.iloc[train_index], y.iloc[test_index]  # iloc を使用

    # モデルの学習
    model.fit(X_train, y_train)

    # テストデータでの予測
    y_pred = model.predict(X_test)

    # 評価指標の計算
    mse = mean_squared_error(y_test, y_pred)
    rmse = np.sqrt(mse)
    mae = mean_absolute_error(y_test, y_pred)
    r2 = r2_score(y_test, y_pred)

    # 評価指標のリストに追加
    mse_scores.append(mse)
    rmse_scores.append(rmse)
    mae_scores.append(mae)
    r2_scores.append(r2)

# 各フォールドの評価指標を表示
for i in range(len(mse_scores)):
    print(f"Fold {i+1}:")
    print(f"  MSE: {mse_scores[i]:.2f}")
    print(f"  RMSE: {rmse_scores[i]:.2f}")
    print(f"  MAE: {mae_scores[i]:.2f}")
    print(f"  R^2: {r2_scores[i]:.2f}")

# 評価指標の平均値を表示
print("\nAverage Scores:")
print(f"  MSE: {np.mean(mse_scores):.2f}")
print(f"  RMSE: {np.mean(rmse_scores):.2f}")
print(f"  MAE: {np.mean(mae_scores):.2f}")
print(f"  R^2: {np.mean(r2_scores):.2f}") 

Repeated K-fold CV

• from sklearn.model_selection import KFold, RepeatedKFold
• K-Fold CVを複数回実施
• n_repeats引数に回数を指定する
• 他の使い方はKFoldクラスと同様

from sklearn.model_selection import KFold, RepeatedKFold
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import pandas as pd

# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv")  

# 前処理
# 欠損値の処理
imputer = SimpleImputer(strategy='mean')
numerical_cols = df.select_dtypes(include=np.number).columns
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数の処理
categorical_cols = df.select_dtypes(include='object').columns
ohe = OneHotEncoder(handle_unknown='ignore', sparse_output=False)
encoded_data = ohe.fit_transform(df[categorical_cols])
encoded_df = pd.DataFrame(encoded_data, columns=ohe.get_feature_names_out(categorical_cols))
df = pd.concat([df, encoded_df], axis=1)
df = df.drop(categorical_cols, axis=1)

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# K分割交差検証の設定
kf = KFold(n_splits=5, shuffle=True, random_state=42)
rkf = RepeatedKFold(n_splits=5, n_repeats=3, random_state=42)

# モデルのインスタンスを作成
model = LinearRegression()

def evaluate_model(model, X, y, cv):
    mse_scores = []
    for train_index, test_index in cv.split(X):
        X_train, X_test = X.iloc[train_index], X.iloc[test_index]
        y_train, y_test = y.iloc[train_index], y.iloc[test_index]
        model.fit(X_train, y_train)
        y_pred = model.predict(X_test)
        mse = mean_squared_error(y_test, y_pred)
        mse_scores.append(mse)
    print(f"Mean MSE: {np.mean(mse_scores):.2f}")

print("K-Fold Cross-Validation:")
evaluate_model(model, X, y, kf)

print("\nRepeated K-Fold Cross-Validation:")
evaluate_model(model, X, y, rkf) 

出力：

K-Fold Cross-Validation:
Mean MSE: 0.14

Repeated K-Fold Cross-Validation:
Mean MSE: 0.13

Pipeline

タイタニックデータセットに対して、パイプラインと K分割交差検証を用いた線形回帰モデルの評価を行うことができます。

Pipeline + KFold

• from sklearn.pipeline import Pipeline
• Pipeline を使用して、標準化と線形回帰のパイプラインを作成します。
• パイプラインを使用することで、前処理とモデル学習をまとめて実行できます。

from sklearn.model_selection import KFold, cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder
import numpy as np
import pandas as pd

# タイタニックデータセットの読み込み
df = pd.read_csv("titanic.csv")  

# 前処理
# 欠損値の処理
imputer = SimpleImputer(strategy='mean')
numerical_cols = df.select_dtypes(include=np.number).columns
df[numerical_cols] = imputer.fit_transform(df[numerical_cols])

# カテゴリカル変数の処理
categorical_cols = df.select_dtypes(include='object').columns
ohe = OneHotEncoder(handle_unknown='ignore', sparse_output=False)
encoded_data = ohe.fit_transform(df[categorical_cols])
encoded_df = pd.DataFrame(encoded_data, columns=ohe.get_feature_names_out(categorical_cols))
df = pd.concat([df, encoded_df], axis=1)
df = df.drop(categorical_cols, axis=1)

# 説明変数と目的変数の設定
X = df.drop('Survived', axis=1)
y = df['Survived']

# パイプラインの作成
pipeline = Pipeline(steps=[
    ('scaler', StandardScaler()),
    ('model', LinearRegression())
])

# 交差検証の実行
cv = KFold(n_splits=5, shuffle=True, random_state=0)
scores = cross_val_score(pipeline, X, y, scoring='neg_mean_squared_error', cv=cv)

# 結果の出力
print(f"Cross-validation scores: {scores}")
print(f"Mean MSE: {-scores.mean():.2f}") 

Leave-One-Out Cross-Validation (LOOCV)

Leave-One-Out Cross-Validation (LOOCV)は、より厳密な交差検証の手法です。この手法では、データセットの各サンプルを一度ずつ検証データとして使用し、残りのすべてのサンプルを訓練データとして使用します。具体的な流れは以下の通りです。

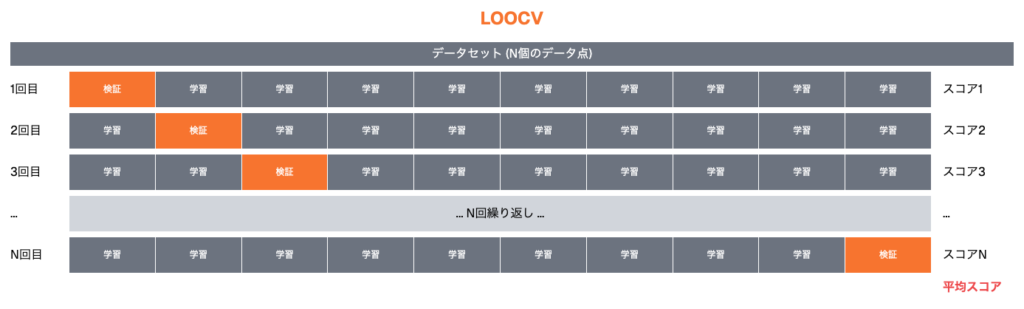
ステップ	説明
検証データの選択	各サンプルを1つの検証データとして選びます。
モデルの訓練	残りのサンプルを使用してモデルを訓練します。
性能評価	検証データに対するモデルの性能を評価します。
スコアの平均	すべてのサンプルについて性能を評価した後、その平均を取ります。

利点と欠点：

LOOCVの利点は、モデルの性能を非常に詳細に評価できる点ですが、計算量が多くなるため、データセットが大きい場合には時間がかかることがあります。

from sklearn.model_selection import LeaveOneOut, cross_val_score
from sklearn.linear_model import LogisticRegression

# Leave-One-Out Cross-Validationの設定
loo = LeaveOneOut()

# モデルのインスタンスを作成
model = LogisticRegression()

# cross_val_score に n_jobs=-1 を指定
scores = cross_val_score(model, X, y, cv=loo, n_jobs=-1) 

print(f"Mean Score with LOOCV: {scores.mean():.2f}")

交差検証は、モデルの性能を評価し、過学習を防ぐための強力な手法です。K分割交差検証は一般的で信頼性が高い手法であり、LOOCVはより厳密な評価が可能ですが、計算コストが高くなります。これらの手法を適切に活用することで、より高い汎化性能を持つモデルを構築することができます。

【第5回】モデル評価と最適化（前編）はここまでです。前編は分類、回帰、交差検証などのモデル評価を扱った回になりました。次回の後編は様々なモデルの最適化手法を扱った回になりますのでよろしくお願いします!